Skip to main content
Global

10.5：使用对数的属性

  1. Last updated
  2. Save as PDF
  • Page ID
    204033

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 使用对数的属性
    • 使用 “更改基本公式”

    在开始之前，请参加这个准备测验。

    1. 评估：a.\(a^{0}\) b\(a^{1}\).
      如果您错过了此问题，请查看示例 5.14。
    2. 用有理指数书写:\(\sqrt[3]{x^{2} y}\).
      如果您错过了此问题，请查看示例 8.27。
    3. 四舍五入到小数点后三位:\(2.5646415\).
      如果你错过了这个问题，请查看示例 1.34。

    使用对数的属性

    既然我们已经了解了指数函数和对数函数，我们可以介绍一些对数的属性。 在我们继续求解指数方程和对数方程时，这些将非常有用。

    前两个属性源自对数的定义。 因为\(a^{0}=1\)，我们可以将其转换为对数形式并得到\(\log _{a} 1=0\)。 另外，从那以后\(a^{1}=a\)，我们明白\(\log _{a} a=1\)了。

    定义\(\PageIndex{1}\)

    对数的属性

    \(\log _{a} 1=0 \quad \log _{a} a=1\)

    在下一个示例中，我们可以像之前一样通过转换为指数形式来计算对数，但是识别然后应用这些属性可以节省时间。

    示例\(\PageIndex{1}\)

    使用对数的属性进行计算：

    1. \(\log _{8} 1\)
    2. \(\log _{6} 6\)

    解决方案：

    一个。

    \(\log _{8} 1\)

    使用该属性，\(\log _{a} 1=0\)。

    \(0 \quad \log _{8} 1=0\)

    b。

    \(\log _{6} 6\)

    使用该属性，\(\log _{a} a=1\)。

    \(1 \quad \log _{6} 6=1\)

    练习\(\PageIndex{1}\)

    使用对数的属性进行计算：

    1. \(\log _{13} 1\)
    2. \(\log _{9} 9\)
    回答
    1. \(0\)
    2. \(1\)
    练习\(\PageIndex{2}\)

    使用对数的属性进行计算：

    1. \(\log _{5} 1\)
    2. \(\log _{7} 7\)
    回答
    1. \(0\)
    2. \(1\)

    接下来的两个属性也可以通过将它们从指数形式转换为对数形式或反之来进行验证。

    指数方程\(a^{\log _{a} x}=x\)转换为对数方程\(\log _{a} x=\log _{a} x\)，这是\(x\)仅表示正值的真实陈述。

    对数方程\(\log _{a} a^{x}=x\)转换为指数方程\(a^{x}=a^{x}\)，这也是真实的陈述。

    这两个属性被称为反向属性，因为当我们有相同的基数时，将日志 “撤消” 为幂并使日志 “撤消” 为次方。 这两个属性显示了函数的构成。 两者最终都得到了恒等函数，它再次表明指数和对数函数是反函数。

    定义\(\PageIndex{2}\)

    对数的反向属性

    对于\(a>0, x>0\) and\(a \neq 1\)，

    \(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)

    在下一个示例中，应用对数的逆属性。

    示例\(\PageIndex{2}\)

    使用对数的属性进行计算：

    1. \(4^{\log _{4} 9}\)
    2. \(\log _{3} 3^{5}\)

    解决方案：

    一个。

    \(4^{\log _{4} 9}\)

    使用该属性，\(a^{\log _{a} x}=x\)。

    \(9 \quad 4^{\log _{4} 9}=9\)

    b。

    \(\log _{3} 3^{5}\)

    使用该属性，\(a^{\log _{a} x}=x\)。

    \(5 \quad \log _{3} 3^{5}=5\)

    练习\(\PageIndex{3}\)

    使用对数的属性进行计算：

    1. \(5^{\log _{5} 15}\)
    2. \(\log _{7} 7^{4}\)
    回答
    1. \(15\)
    2. \(4\)
    练习\(\PageIndex{4}\)

    使用对数的属性进行计算：

    1. \(2^{\log _{2} 8}\)
    2. \(\log _{2} 2^{15}\)
    回答
    1. \(8\)
    2. \(15\)

    对数还有另外三个属性将在我们的工作中很有用。 我们知道指数函数和对数函数密切相关。 我们对对数的定义向我们表明，对数是等效指数的指数。 指数的属性具有指数的相关属性。

    在指数的乘积属性中\(a^{m} \cdot a^{n}=a^{m+n}\)，我们可以看到，要乘以相同的基数，我们将指数相加。 对数的乘积属性\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)告诉我们获取产品的日志，我们添加因子对数。

    定义\(\PageIndex{3}\)

    对数的乘积属性

    如果\(M>0, N>0, \mathrm{a}>0\)\(\mathrm{a} \neq 1,\)然后再说

    \(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\)

    乘积的对数是对数之和。

    我们使用此属性将产品的日志写入为每个因子的日志之和。

    示例\(\PageIndex{3}\)

    使用对数的乘积属性将每个对数写成对数之和。 尽可能简化：

    1. \(\log _{3} 7 x\)
    2. \(\log _{4} 64 x y\)

    解决方案：

    一个。

    \(\log _{3} 7 x\)

    使用产品属性，\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\)。

    \(\log _{3} 7+\log _{3} x\)
    \(\log _{3} 7 x=\log _{3} 7+\log _{3} x\)

    b。

    \(\log _{4} 64 x y\)

    使用产品属性，\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\)。

    \(\log _{4} 64+\log _{4} x+\log _{4} y\)

    简化评估，\(\log _{4} 64\)。

    \(3+\log _{4} x+\log _{4} y\)
    \(\log _{4} 64 x y=3+\log _{4} x+\log _{4} y\)

    练习\(\PageIndex{5}\)

    使用对数的乘积属性将每个对数写成对数之和。 尽可能简化：

    1. \(\log _{3} 3 x\)
    2. \(\log _{2} 8 x y\)
    回答
    1. \(1+\log _{3} x\)
    2. \(3+\log _{2} x+\log _{2} y\)
    练习\(\PageIndex{6}\)

    使用对数的乘积属性将每个对数写成对数之和。 尽可能简化：

    1. \(\log _{9} 9 x\)
    2. \(\log _{3} 27 x y\)
    回答
    1. \(1+\log _{9} x\)
    2. \(3+\log _{3} x+\log _{3} y\)

    同样，在指数的商属性中，我们可以看到\(\frac{a^{m}}{a^{n}}=a^{m-n}\)，要除以相同的基数，我们减去指数。 对数的商属性\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)告诉我们取商的对数，我们减去分子和分母的对数。

    定义\(\PageIndex{4}\)

    对数的商属性

    如果\(M>0, N>0, \mathrm{a}>0\)\(\mathrm{a} \neq 1,\)然后再说

    \(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)

    商的对数是对数之差。

    请注意\(\log _{a} M=\log _{a} N \not=\log _{a}(M-N)\)。

    我们使用这个属性将商的对数写成每个因子对数的差。

    示例\(\PageIndex{4}\)

    使用对数的商属性将每个对数写成对数之差。 尽可能简化。

    1. \(\log _{5} \frac{5}{7}\)
    2. \(\log \frac{x}{100}\)

    解决方案：

    一个。

    \(\log _{5} \frac{5}{7}\)

    使用商属性，\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)。

    \(\log _{5} 5-\log _{5} 7\)

    简化。

    \(1-\log _{5} 7\)

    \(\log _{5} \frac{5}{7}=1-\log _{5} 7\)

    b。

    \(\log \frac{x}{100}\)

    使用商属性，\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)。

    \(\log x-\log 100\)

    简化。

    \(\log x-2\)

    \(\log \frac{x}{100}=\log x-2\)

    练习\(\PageIndex{7}\)

    使用对数的商属性将每个对数写成对数之差。 尽可能简化。

    1. \(\log _{4} \frac{3}{4}\)
    2. \(\log \frac{x}{1000}\)
    回答
    1. \(\log _{4} 3-1\)
    2. \(\log x-3\)
    练习\(\PageIndex{8}\)

    使用对数的商属性将每个对数写成对数之差。 尽可能简化。

    1. \(\log _{2} \frac{5}{4}\)
    2. \(\log \frac{10}{y}\)
    回答
    1. \(\log _{2} 5-2\)
    2. \(1-\log y\)

    对数的第三个属性与指数的幂属性有关，我们可以看到\(\left(a^{m}\right)^{n}=a^{m \cdot n}\)，要将乘以指数，将乘以次方。 Logarithms 的幂属性\(\log _{a} M^{p}=p \log _{a} M\)告诉我们取一个数字的对数为乘方，我们将乘以该数字的对数。

    定义\(\PageIndex{5}\)

    对数的幂属性

    如果\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\) an\(p\) d 是任何实数，那么

    \(\log _{a} M^{p}=p \log _{a} M\)

    将一个数字提升为幂的对数，该乘积乘以该数字的对数。

    我们使用这个属性来写一个数字的日志，该数字的乘积是该数字的乘积乘以该数字的对数。 我们本质上是取指数并将其放在对数的前面。

    示例\(\PageIndex{5}\)

    使用对数的幂属性将每个对数写成对数的乘积。 尽可能简化。

    1. \(\log _{5} 4^{3}\)
    2. \(\log x^{10}\)

    解决方案：

    一个。

    \(\log _{5} 4^{3}\)

    使用电源属性，\(\log _{a} M^{p}=p \log _{a} M\)。

    3\(\log _{5} 4\)

    \(\log _{5} 4^{3}=3 \log _{5} 4\)

    b。

    \(\log x^{10}\)

    使用电源属性，\(\log _{a} M^{p}=p \log _{a} M\)。

    \(10\log x\)

    \(\log x^{10}=10 \log x\)

    练习\(\PageIndex{9}\)

    使用对数的幂属性将每个对数写成对数的乘积。 尽可能简化。

    1. \(\log _{7} 5^{4}\)
    2. \(\log x^{100}\)
    回答
    1. \(4\log _{7} 5\)
    2. 100\(\cdot \log x\)
    练习\(\PageIndex{10}\)

    使用对数的幂属性将每个对数写成对数的乘积。 尽可能简化。

    1. \(\log _{2} 3^{7}\)
    2. \(\log x^{20}\)
    回答
    1. \(7\log _{2} 3\)
    2. \(20\cdot \log x\)

    为了便于参考，我们在此总结了对数的属性。 虽然自然对数是这些属性的特例，但同时显示每个属性的自然对数版本通常很有帮助。

    对数的属性

    如果\(M>0, \mathrm{a}>0, \mathrm{a} \neq 1\) an\(p\) d 是任何实数，那么

    财产 基地\(a\) 基地\(e\)
    \ (a\)” >\(\log _{a} 1=0\) \ (e\) ">\(\ln 1=0\)
    \ (a\)” >\(\log _{a} a=1\) \ (e\) ">\(\ln e=1\)
    反向特性 \ (a\)” >\(a^{\log _{a} x}=x\)
    \(\log _{a} a^{x}=x\)    		 \ (e\) ">\(e^{\ln x}=x\)
    \(\ln e^{x}=x\)
    对数的乘积属性 \ (a\)” >\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) \ (e\) ">\(\ln (M \cdot N)=\ln M+\ln N\)
    对数的商性质 \ (a\)” >\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) \ (e\) ">\(\ln \frac{M}{N}=\ln M-\ln N\)
    对数的幂属性 \ (a\)” >\(\log _{a} M^{p}=p \log _{a} M\) \ (e\) ">\(\ln M^{p}=p \ln M\)
    表 10.4.1

    现在我们有了这些属性，我们可以用它们来 “扩展” 对数表达式。 这意味着将对数写成总和或差值，没有任何幂次方。

    在应用 Power Property 之前，我们通常会应用乘积和商数属性。

    示例\(\PageIndex{6}\)

    使用对数属性来扩展对数\(\log _{4}\left(2 x^{3} y^{2}\right)\)。 尽可能简化。

    解决方案：

    使用产品属性，\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)。

    在最后两个术语中使用 Power 属性。\(\log _{a} M^{p}=p \log _{a} M\) 简化。

    练习\(\PageIndex{11}\)

    使用对数属性来扩展对数\(\log _{2}\left(5 x^{4} y^{2}\right)\)。 尽可能简化。

    回答

    \(\log _{2} 5+4 \log _{2} x+2 \log _{2} y\)

    练习\(\PageIndex{12}\)

    使用对数属性来扩展对数\(\log _{3}\left(7 x^{5} y^{3}\right)\)。 尽可能简化。

    回答

    \(\log _{3} 7+5 \log _{3} x+3 \log _{3} y\)

    当我们在对数表达式中有激进时，首先将其激进写成有理指数会很有帮助。

    示例\(\PageIndex{7}\)

    使用对数属性来扩展对数\(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\)。 尽可能简化。

    解决方案

    \(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}\)

    用有理指数重写激进。

    \(\log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)^{\frac{1}{4}}\)

    使用电源属性，\(\log _{a} M^{p}=p \log _{a} M\)。

    \(\frac{1}{4} \log _{2}\left(\frac{x^{3}}{3 y^{2} z}\right)\)

    使用商属性，\(\log _{a} M \cdot N=\log _{a} M-\log _{a} N\)。

    \(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\log _{2}\left(3 y^{2} z\right)\right)\)

    在第二个学期\(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)中使用产品属性。

    \(\frac{1}{4}\left(\log _{2}\left(x^{3}\right)-\left(\log _{2} 3+\log _{2} y^{2}+\log _{2} z\right)\right)\)

    使用括号内\(\log _{a} M^{p}=p \log _{a} M\)的 Power 属性。

    \(\frac{1}{4}\left(3 \log _{2} x-\left(\log _{2} 3+2 \log _{2} y+\log _{2} z\right)\right)\)

    通过分发进行简化。

    \(\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)

    \(\log _{2} \sqrt[4]{\frac{x^{3}}{3 y^{2} z}}=\frac{1}{4}\left(3 \log _{2} x-\log _{2} 3-2 \log _{2} y-\log _{2} z\right)\)

    练习\(\PageIndex{13}\)

    使用对数属性来扩展对数\(\log _{4} \sqrt[5]{\frac{x^{4}}{2 y^{3} z^{2}}}\)。 尽可能简化。

    回答

    \(\frac{1}{5}\left(4 \log _{4} x-\frac{1}{2}-3 \log _{4} y-2 \log _{4} z\right)\)

    练习\(\PageIndex{14}\)

    使用对数属性来扩展对数\(\log _{3} \sqrt[3]{\frac{x^{2}}{5 y z}}\)。 尽可能简化。

    回答

    \(\frac{1}{3}\left(2 \log _{3} x-\log _{3} 5-\log _{3} y-\log _{3} z\right)\)

    扩展对数的反面是将具有相同底数的对数的总和或差压缩为单个对数。 我们再次使用对数的属性来帮助我们，但恰恰相反。

    为了将具有相同底数的对数表达式压缩成一个对数，我们首先使用 Power Property 将对数项的系数转换为一，然后根据需要使用乘积和商属性。

    示例\(\PageIndex{8}\)

    使用对数属性来压缩对数\(\log _{4} 3+\log _{4} x-\log _{4} y\)。 如果可能，请简化。

    解决方案：

    所有日志表达式的基数都相同\(4\)。

    添加了前两个术语，因此我们使用产品属性\(\log _{a} M+\log _{a} N=\log _{a} M : N\)。

    由于减去了日志，因此我们使用商属性\(\log _{a} M-\log _{a} N=\log _{a} \frac{M}{N}\)。

    练习\(\PageIndex{15}\)

    使用对数属性来压缩对数\(\log _{2} 5+\log _{2} x-\log _{2} y\)。 如果可能，请简化。

    回答

    \(\log _{2} \frac{5 x}{y}\)

    练习\(\PageIndex{16}\)

    使用对数属性来压缩对数\(\log _{3} 6-\log _{3} x-\log _{3} y\)。 如果可能，请简化。

    回答

    \(\log _{3} \frac{6}{x y}\)

    示例\(\PageIndex{9}\)

    使用对数属性来压缩对数\(2 \log _{3} x+4 \log _{3}(x+1)\)。 如果可能，请简化。

    解决方案：

    日志表达式的基数相同\(3\)。

    \(2 \log _{3} x+4 \log _{3}(x+1)\)

    使用电源属性，\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\)。

    \(\log _{3} x^{2}+\log _{3}(x+1)^{4}\)

    术语已添加，因此我们使用产品属性\(\log _{a} M+\log _{a} N=\log _{a} M \cdot N\)。

    \(\log _{3} x^{2}(x+1)^{4}\)
    \(2 \log _{3} x+4 \log _{3}(x+1)=\log _{3} x^{2}(x+1)^{4}\)

    练习\(\PageIndex{17}\)

    使用对数属性来压缩对数\(3 \log _{2} x+2 \log _{2}(x-1)\)。 如果可能，请简化。

    回答

    \(\log _{2} x^{3}(x-1)^{2}\)

    练习\(\PageIndex{18}\)

    使用对数属性来压缩对数\(2 \log x+2 \log (x+1)\)。 如果可能，请简化。

    回答

    \(\log x^{2}(x+1)^{2}\)

    使用基数变更公式

    要使用任何其他基数计算对数，我们可以使用 Change-of-base 公式。 我们将展示这是如何得出的。

    \(\begin{array} {l c} {\text{Suppose we want to evaluate} \log_{a}M} & {\log_{a}M} \\ {\text{Let} \:y =\log_{a}M. }&{y=\log_{a}M} \\ {\text{Rewrite the epression in exponential form. }}&{a^{y}=M } \\ {\text{Take the }\:\log_{b} \text{of each side.}}&{\log_{b}a^{y}=\log_{b}M}\\ {\text{Use the Power Property.}}&{y\log_{b}a=\log_{b}M} \\ {\text{Solve for}\:y. }&{y=\frac{\log_{b}M}{\log_{b}a}} \\ {\text{Substiture}\:y=\log_{a}M.}&{\log_{a}M=\frac{\log_{b}M}{\log_{b}a}} \end{array}\)

    基础变更公式引入了新的基础\(b\)。 这可以是\(b\)我们想要的任何基地\(b>0,b≠1\)。 因为我们的计算器有对数基数\(10\)和基数的键\(e\)，所以我们将使用新的基数作为\(10\)或来重写基数变化公式\(e\)。

    定义\(\PageIndex{6}\)

    基数变更公式

    对于任何对数基数\(a, b\)\(M>0\)和

    \(\begin{array}{lll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)

    当我们使用计算器求对数值时，我们通常四舍五入到小数点后三位。 这为我们提供了一个近似值，因此我们使用大致相等的符号\((≈)\)。

    示例\(\PageIndex{10}\)

    四舍五入到小数点后三位，近似值\(\log _{4} 35\)。

    解决方案：

      。
    使用基数变更公式。 。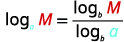
    识别\(a\)和\(M\). \(10\)选择\(b\). 。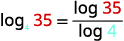
    使用基数的日志按钮\(\frac{\log 35}{\log 4}\)在计算器中输入表达式\(10\)。 四舍五入到小数点后三位。 。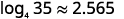
    表 10.4.2
    练习\(\PageIndex{19}\)

    四舍五入到小数点后三位，近似值\(\log _{3} 42\)。

    回答

    \(3.402\)

    练习\(\PageIndex{20}\)

    四舍五入到小数点后三位，近似值\(\log _{5} 46\)。

    回答

    \(2.379\)

    访问这些在线资源以获取更多指导，并使用对数的属性进行练习。

    关键概念

    • \(\log _{a} 1=0 \quad \log _{a} a=1\)
    • 对数的反向性质
      • For an\(a>0,x>0\) d\(a≠1\)

        \(a^{\log _{a} x}=x \quad \log _{a} a^{x}=x\)

    • 对数的乘积属性
      • 如果\(M>0,N>0,a>0\)和\(a≠1\)，那么

        \(\log _{a} M \cdot N=\log _{a} M+\log _{a} N\)

        乘积的对数是对数之和。
    • 对数的商性质
      • 如果\(M>0, N>0, \mathrm{a}>0\)和\(a≠1\)，那么

        \(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\)

        商的对数是对数之差。
    • 对数的幂属性
      • 如果\(M>0,a>0,a≠1\) an\(p\) d 是任何实数，那么

        \(\log _{a} M^{p}=p \log _{a} M\)

        将数字提升为幂的对数是功率乘以该数字的对数的乘积。
    • 对数的属性摘要
      如果\(M>0,a>0,a≠1\)和\(p\)是任何实数，那么，
    财产 基地\(a\) 基地\(e\)
    \ (a\)” >\(\log _{a} 1=0\) \ (e\) ">\(\ln 1=0\)
    \ (a\)” >\(\log _{a} a=1\) \ (e\) ">\(\ln e=1\)
    反向特性 \ (a\)” >\(a^{\log _{a} x}=x\)
    \(\log _{a} a^{x}=x\)    		 \ (e\) ">\(e^{\ln x}=x\)
    \(\ln e^{x}=x\)
    对数的乘积属性 \ (a\)” >\(\log _{a}(M \cdot N)=\log _{a} M+\log _{a} N\) \ (e\) ">\(\ln (M \cdot N)=\ln M+\ln N\)
    对数的商性质 \ (a\)” >\(\log _{a} \frac{M}{N}=\log _{a} M-\log _{a} N\) \ (e\) ">\(\ln \frac{M}{N}=\ln M-\ln N\)
    对数的幂属性 \ (a\)” >\(\log _{a} M^{p}=p \log _{a} M\) \ (e\) ">\(\ln M^{p}=p \ln M\)
    表 10.4.1
    • 基数变化公式
      适用于任何对数基数\(a\)和\(b\)\(M>0\)，

      \(\begin{array}{ll}{\log _{a} M=\frac{\log _{b} M}{\log _{b} a}} & {\log _{a} M=\frac{\log M}{\log a}} & {\log _{a} M=\frac{\ln M}{\ln a}} \\ {\text { new base } b} & {\text { new base } 10} & {\text { new base } e}\end{array}\)