10.2: 查找复合函数和逆函数
- Page ID
- 203998
在本节结束时,您将能够:
- 查找和计算复合函数
- 确定一个函数是否是一对一的
- 求函数的逆函数
在开始之前,请参加这个准备测验。
- 如果\(f(x)=2 x-3\)和\(g(x)=x^{2}+2 x-3\),则查找\(f(4)\)。
如果你错过了这个问题,请查看示例 3.48。 - 求解\(x\),\(3x+2y=12\)。
如果你错过了这个问题,请查看示例 2.31。 - 简化:\(5 \frac{(x+4)}{5}-4\)。
如果你错过了这个问题,请查看示例 1.25。
在本章中,我们将介绍两种新的函数类型:指数函数和对数函数。 正如我们将看到的那样,这些功能在商业和科学领域被广泛使用。
查找和计算复合函数
在介绍函数之前,我们需要看一下函数的另一种操作,即组合函数。 在合成中,一个函数的输出是第二个函数的输入。 对于函数\(f\)和\(g\),组合由编写\(f∘g\)和定义\((f∘g)(x)=f(g(x))\)。
我们读\(f(g(x))\)作 “o\(f\) f o\(g\) f”\(x\)。
要进行合成,第一个函数的输出将成为第二个函数的输入\(f\),因此我们必须确保它是的域的一部分\(f\)。\(g(x)\)
函数\(f\)和\(g\)的组成由下\(f \cdot g\)式编写和定义
\((f \circ g)(x)=f(g(x))\)
\(f(g(x))\)截至目前,我们\(f\)已\(g\)阅读\(x\)。
实际上,我们以前曾多次使用合成而不使用符号。 当我们使用平移绘制二次函数时,我们是在组合函数。 例如,如果我们首先绘制\(g(x)=x^{2}\)为抛物线,然后将其垂直向下移动四个单位,则我们使用的是由 where 定义\((f∘g)(x)=f(g(x))\)的构图\(f(x)=x−4\)。
对于函数\(f(x)=4x-5\)和\(g(x)=2x+3\),请查找
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
解决方案:
-
使用... 的定义\((f \circ g)(x)\)。 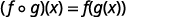

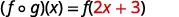

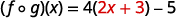
分发。 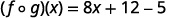
简化。 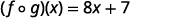
表 10.1.1 -
使用... 的定义\((f \circ g)(x)\)。 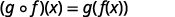

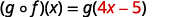

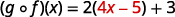
分发。 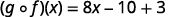
简化。 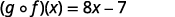
表 10.1.2
注意部分 a 和 b 部分的结果不同。
c. 注意\((f \cdot g)(x)\)这与不同\((f \circ g)(x)\)。 在 a 部分中,我们做了函数的构成。 现在在 c 部分中,我们不是在合成它们,而是在乘以它们。
使用... 的定义\((f \cdot g)(x)\)。
\((f \cdot g)(x)=f(x) \cdot g(x)\)
替换\(f(x)=4 x-5\)和\(g(x)=2 x+3\).
\((f \cdot g)(x)=(4 x-5) \cdot(2 x+3)\)
乘以。
\((f \cdot g)(x)=8 x^{2}+2 x-15\)
对于函数\(f(x)=3x-2\)和\(g(x)=5x+1\),请查找
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- 回答
-
- \(15x+1\)
- \(15x-9\)
- \(15 x^{2}-7 x-2\)
对于函数\(f(x)=4 x-3\)\(g(x)=6x-5\),请查找
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- 回答
-
- \(24 x-23\)
- \(24 x-23\)
- \(24 x^{2}-38 x+15\)
在下一个示例中,我们将评估特定值的构图。
对于 functions 和\(f(x)=x^{2}-4\)\(g(x)=3 x+2\),请查找:
- \((f \circ g)(-3)\)
- \((g \circ f)(-1)\)
- \((f \circ f)(2)\)
解决方案:
-
使用... 的定义\((f \circ g)(-3)\)。 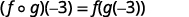

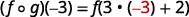
简化。 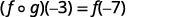

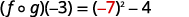
简化。 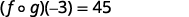
表 10.1.3 -
使用... 的定义\((g \circ f)(-1)\)。 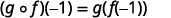

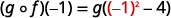
简化。 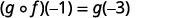

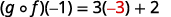
简化。 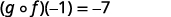
表 10.1.4 -
使用... 的定义\((f \circ f)(2)\)。 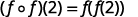

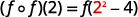
简化。 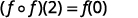

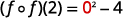
简化。 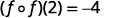
表 10.1.5
对于函数\(f(x)=x^{2}-9\)\(g(x)=2x+5\),请查找
- \((f \circ g)(-2)\)
- \((g \circ f)(-3)\)
- \((f \circ f)(4)\)
- 回答
-
- \(-8\)
- \(5\)
- \(40\)
对于函数\(f(x)=x^{2}+1\)\(g(x)=3x-5\),请查找
- \((f \circ g)(-1)\)
- \((g \circ f)(2)\)
- \((f \circ f)(-1)\)
- 回答
-
- \(65\)
- \(10\)
- \(5\)
确定函数是否为一对一函数
当我们第一次引入函数时,我们说函数是一种关系,它为其域中的每个元素分配一个区间中的一个元素。 对于关系中的每个有序对,每个\(x\)-value 仅与一个\(y\)-value 匹配。
我们使用生日示例来帮助我们理解定义。 每个人都有生日,但没有人有两个生日,两个人共享生日是可以的。 由于每个人只有一个生日,所以这种关系是一种功能。

如果范围中的每个值在域中只有一个元素,则函数为一对一。 对于函数中的每个有序对,每个 y 值仅与一个\(x\)-value 匹配。
我们的生日关系示例不是一对一的函数。 两个人可以共享同一个生日。 8 月 2 日的区间值是 Liz 和 6 月的生日,因此一个区间值有两个域值。 因此,该函数不是一对一的。
如果范围内的每个值对应于域中的一个元素,则函数为一对一。 对于函数中的每个有序对,每个\(y\)-value 仅与一个\(x\)-value 匹配。 没有重复的\(y\)-values。
对于每组有序对,确定它是否代表一个函数,如果是,则确定该函数是否为一对一。
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
解决方案:
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
每个\(x\)-value 仅与一个\(y\)-value 匹配。 因此,这种关系是一种函数。
但是每个\(y\)-value 不只与一个\(x\)-value 配对\((3,27)\),例如。\((−3,27)\) 所以这个函数不是一对一的。
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
每个\(x\)-value 仅与一个\(y\)-value 匹配。 因此,这种关系是一种函数。
由于每个\(y\)-value 仅与一个\(x\)-value 配对,因此此函数是一对一的。
对于每组有序对,确定它是否代表一个函数,如果是,则是一对一的函数。
- \(\{(-3,-6),(-2,-4),(-1,-2),(0,0),(1,2),(2,4),(3,6)\}\)
- \(\{(-4,8),(-2,4),(-1,2),(0,0),(1,2),(2,4),(4,8)\}\)
- 回答
-
- 一对一功能
- 功能;不是一对一
对于每组有序对,确定它是否代表一个函数,如果是,则是一对一的函数。
- \(\{(27,-3),(8,-2),(1,-1),(0,0),(1,1),(8,2),(27,3)\}\)
- \(\{(7,-3),(-5,-4),(8,0),(0,0),(-6,4),(-2,2),(-1,3)\}\)
- 回答
-
- 不是函数
- 功能;不是一对一
为了帮助我们确定关系是否为函数,我们使用垂直线测试。 如果每条垂直线与图形最多相交一个点,则矩形坐标系中的一组点就是函数的图形。 此外,如果有任何垂直线在多个点上与图形相交,则该图不代表函数。
垂直线代表一个\(x\)-value,我们检查它是否仅在一个\(y\)-value中与图形相交。 那么它就是一个函数。
为了检查一个函数是否是一对一的,我们使用了类似的过程。 我们使用水平线,检查每条水平线是否仅在一个点上与图形相交。 水平线代表一个\(y\)-value,我们检查它是否仅在一个\(x\)-value中与图形相交。 如果每条水平线与函数的图形最多相交一点,则它是一对一的函数。 这是水平线测试。
水平线测试
如果每条水平线与函数的图形最多相交一点,则它是一对一的函数。
我们可以使用垂直线测试来测试关系图是否为函数。 然后,我们可以通过应用水平线测试来判断该函数是否是一对一的。
确定
- 每张图是否是函数的图形,如果是,
- 是否是一对一的
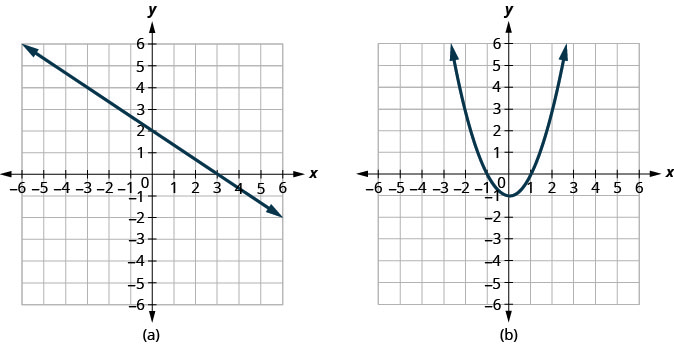
解决方案:
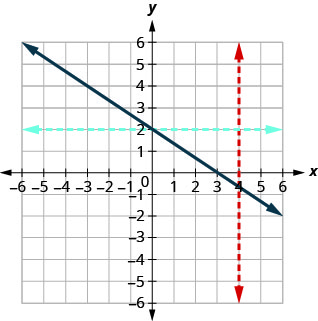
图 10.1.40
由于任何垂直线最多与图形相交一个点,因此该图形是函数的图形。 由于任何水平线最多与图形相交一个点,因此该图形是一对一函数的图形。
b。
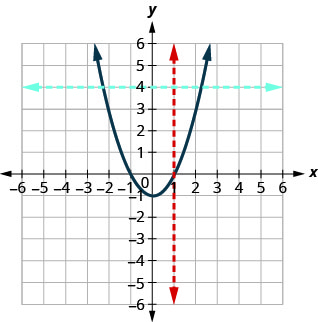
由于任何垂直线最多与图形相交一个点,因此该图形是函数的图形。 图表上显示的水平线将其交叉成两点。 此图不代表一对一的函数。
确定
- 每张图是否是函数的图形,如果是,
- 是否是一对一的
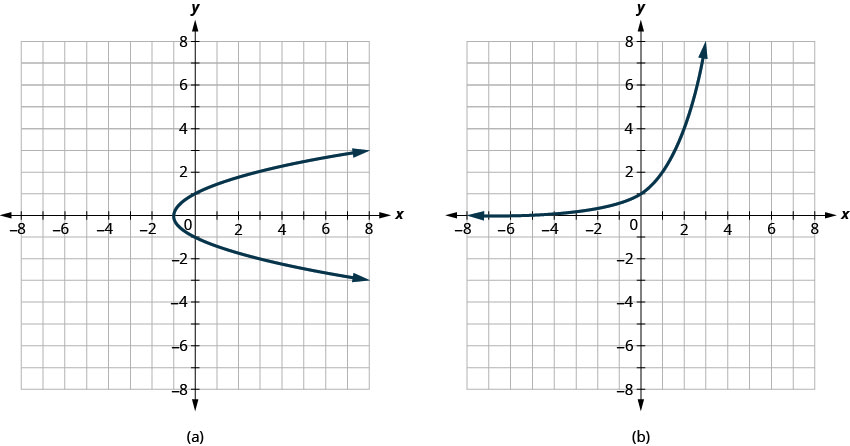
- 回答
-
- 不是函数
- 一对一功能
确定
- 每张图是否是函数的图形,如果是,
- 是否是一对一的
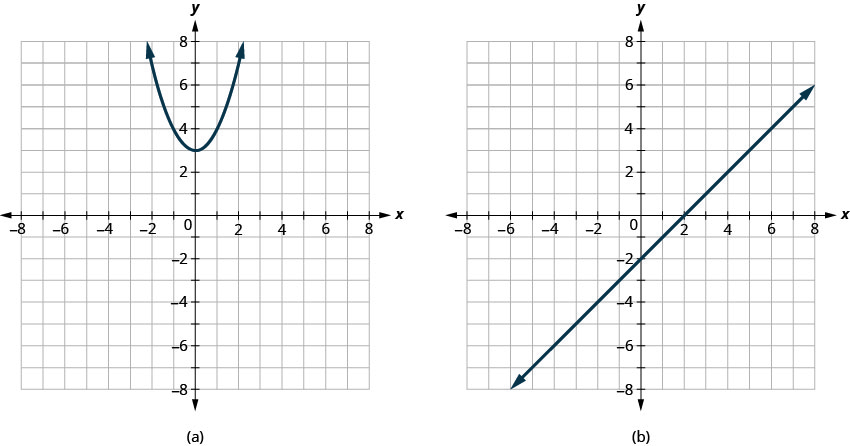
- 回答
-
- 功能;不是一对一
- 一对一功能
求函数的逆函数
让我们来看一个由有序对表示的一对一函数\(\{(0,5),(1,6),(2,7),(3,8)\}\)。\(f\) 对于每个\(x\)-value,相\(f\)加得\(5\)到\(y\)-value。 为了 “撤消” 的加法\(5\),我们\(5\)从每个\(y\)-value中减去并返回到原始的\(x\)-value。 我们可以称之为 “取反向\(f\)” 并命名该函数\(f^{−1}\)。
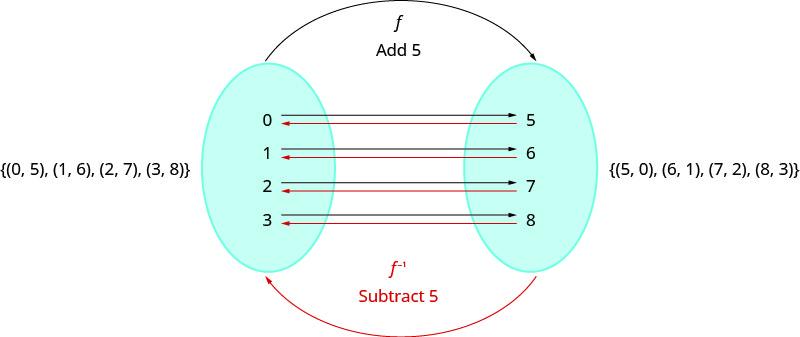
请注意,和的\(f^{−1}\)有序对的-values\(f\) 和\(x\)-val\(y\) ues是相反的。 的域\(f\)是的范围\(f^{−1}\),的域\(f^{−1}\)是的范围\(f\)。
由有序对定义的函数的逆函数
如果\(f(x)\)是一个一对一函数,其有序对的形式为\((x,y)\),则其反函数\(f^{−1}(x)\)是有序对的集合\((y,x)\)。
在下一个示例中,我们将找到由有序对定义的函数的逆函数。
找出函数的逆函数\(\{(0,3),(1,5),(2,7),(3,9)\}\)。 确定逆函数的域和范围。
解决方案:
此函数是一对一的,因为每个\(x\)-value 都只与一个\(y\)-value 配对。
为了找到反向函数,我们将函数的\(x\)有序对中的\(y\)-values和-values进行反转。
\(\begin{array}{ll} {\text{Function}}&{\{(0,3),(1,5),(2,7),(3,9)\}} \\ {\text{Inverse Function}}& {\{(3,0), (5,1), (7,2), (9,3)\}} \\ {\text{Domain of Inverse Function}}&{\{3, 5, 7, 9\}} \\ {\text{Range of Inverse Function}}&{\{0, 1, 2, 3\}} \end{array}\)
找到的反数\(\{(0,4),(1,7),(2,10),(3,13)\}\)。 确定逆函数的域和范围。
- 回答
-
反向函数:\(\{(4,0),(7,1),(10,2),(13,3)\}\). 域:\(\{4,7,10,13\}\)。 范围:\(\{0,1,2,3\}\)。
找到的反数\(\{(-1,4),(-2,1),(-3,0),(-4,2)\}\)。 确定逆函数的域和范围。
- 回答
-
反向函数:\(\{(4,-1),(1,-2),(0,-3),(2,-4)\}\). 域:\(\{0,1,2,4\}\)。 范围:\(\{-4,-3,-2,-1\}\)。
我们刚才注意到,如果\(f(x)\)是一个一对一的函数,其有序对的形式为\((x,y)\),那么它的逆函数\(f^{−1}(x)\)就是有序对的集合\((y,x)\)。
因此,如果一个\((a,b)\)点在函数的图形上\(f(x)\),则有序对\((b,a)\)在的图上\(f^{−1}(x)\)。 参见图 10.1.43。
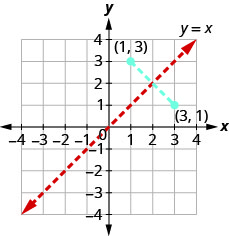
任意两对\((a,b)\)之间的\((b,a)\)距离被直线切成两半\(y=x\)。 所以我们说这些点是彼此通过直线的镜像\(y=x\)。
由于函数\(f(x)\)图上的每个点都是图上某个点的镜像\(f^{−1}(x)\),因此我们说这些图是通过直线相互的镜像\(y=x\)。 在下一个示例中,我们将使用这个概念来绘制函数的逆函数。
在同一个坐标系上绘制图表,显示一对一函数的逆函数。
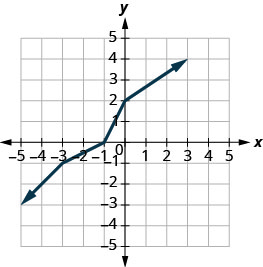
解决方案:
我们可以使用图表上的点来查找反向图上的点。 图上的一些点是:\((−5,−3),(−3,−1),(−1,0),(0,2),(3,4)\).
所以,逆函数将包含点:\((−3,−5),(−1,−3),(0,−1),(2,0),(4,3)\).
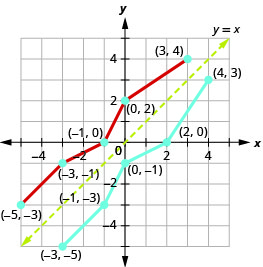
请注意,原始函数的图形和反函数的图是直线的镜像\(y=x\)。
在同一个坐标系上绘制一对一函数的逆函数。
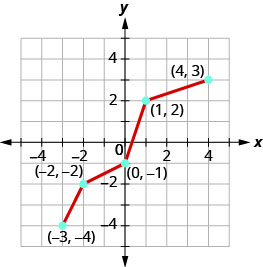
- 回答
-
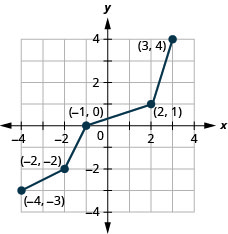
图 10.1.49
在同一个坐标系上绘制一对一函数的逆函数。
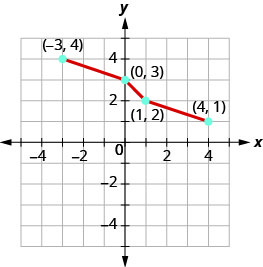
- 回答
-
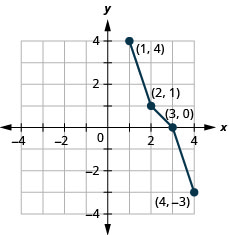
图 10.1.51
当我们开始讨论逆函数时,我们讨论了逆函数如何 “撤消” 原始函数对其域中的值所做的事情,以便恢复到原始的\(x\)-value。

反函数
\(f^{-1}(f(x))=x\),适用于域\(x\)内的所有人\(f\)
\(f\left(f^{-1}(x)\right)=x\),适用于域\(x\)内的所有人\(f^{-1}\)
我们可以使用这个属性来验证两个函数是相反的。
验证\(f(x)=5x−1\)和\(g(x)=\frac{x+1}{5}\)是否为反函数。
解决方案:
如果\(g(f(x))=x\)和,这两个函数是相互反向的\(f(g(x))=x\)。
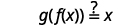 |
|
| 替换\(5x-1\)\(f(x)\)。 | 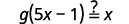 |
 |
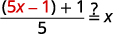 |
| 简化。 | 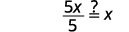 |
| 简化。 | 
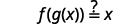
|
| 替代\(\frac{x+1}{5}\)\(g(x)\)。 | 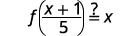 |
 |
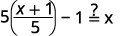 |
| 简化。 | 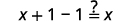 |
| 简化。 |  |
由于\(g(f(x))=x\)和\(f(g(x))=x\)均为真,因此函数\(f(x)=5x−1\)和\(g(x)=\frac{x+1}{5}\)是反函数。 也就是说,它们是彼此的倒数。
验证这些函数是否为反函数。 \(f(x)=4 x-3\)和\(g(x)=\frac{x+3}{4}\)。
- 回答
-
\(g(f(x))=x\),而且\(f(g(x))=x\),所以它们是反向的。
验证这些函数是否为反函数。 \(f(x)=2 x+6\)和\(g(x)=\frac{x-6}{2}\)
- 回答
-
\(g(f(x))=x,\)\(f(g(x))=x,\)所以它们是反向的。
我们发现了由有序对和图形定义的函数的逆函数。 现在,我们将研究如何使用代数方程求逆方程。 该方法采用的思想是,如果\(f(x)\)是具有有序对的一对一函数\((x,y)\),则其逆函数\(f^{−1}(x)\)就是有序对的集合\((y,x)\)。
如果我们反转函数\(y\)中的\(x\)和然后求解\(y\),我们就会得到逆函数。
找到的反数\(f(x)=4 x+7\)。
解决方案:
| 第 1 步。 替代\(y\)\(f(x)\)。 | 替换\(f(x)\)为\(y\)。 | \(\begin{aligned} f(x) &=4 x+7 \\ y &=4 x+7 \end{aligned}\) |
| 步骤 2:交换变量\(x\)和\(y\)。 | 替换\(x\)为,\(y\)然后\(y\)替换为\(x\)。 | \(x=4y+7\) |
| 步骤 3:求解\(y\)。 |
\(7\)从两边减去。 除以\(4\)。 |
\(x-7=4 y\) \(\frac{x-7}{4}=y\) |
| 第 4 步:\(f^{-1}(x)\)替换\(y\)。 | 替换\(y\)为\(f^{-1}(x)\)。 | \(\frac{x-7}{4}=f^{-1}(x)\) |
| 步骤 5:验证函数是否为反向函数。 |
显示\(f^{-1}(f(x))=x\) 和\(f\left(f^{-1}(x)\right)=x\) |
\(\begin{aligned} f^{-1}(f(x)) & \stackrel{?}{=} x \\f^{-1}(4x+7)&\stackrel{?}{=}x\\ \frac{(4x+7)-7}{4}&\stackrel{?}{=}x \\ \frac{4x}{4}&\stackrel{?}{=}x\\x&=x \\ \\f(f^{-1}(x))&\stackrel{?}{=}x \\f \left(\frac{x-7}{4} \right)&\stackrel{?}{=}x \\ 4\left(\frac{x-7}{4} \right) + 7 &\stackrel{?}{=}x \\ x-7+7&\stackrel{?}{=}x \\x&=x \end{aligned}\) |
找出函数的逆函数\(f(x)=5x-3\)。
- 回答
-
\(f^{-1}(x)=\frac{x+3}{5}\)
找出函数的逆函数\(f(x)=8 x+5\)。
- 回答
-
\(f^{-1}(x)=\frac{x-5}{8}\)
我们总结了以下步骤。
如何找到一对一函数的逆函数
- 替代\(y\)\(f(x)\)。
- 交换变量\(x\)和\(y\)。
- 求解\(y\)。
- 替代\(f^{−1}(x)\)\(y\)。
- 验证函数是否为反向函数。
找到的反数\(f(x)=\sqrt[5]{2 x-3}\)。
解决方案:
\(f(x)=\sqrt[5]{2 x-3}\)
替代\(y\)\(f(x)\)。
\(y=\sqrt[5]{2 x-3}\)
交换变量\(x\)和\(y\)。
\(x=\sqrt[5]{2 y-3}\)
求解\(y\)。
\(\begin{aligned}(x)^{5} &=(\sqrt[5]{2 y-3})^{5} \\ x^{5} &=2 y-3 \\ x^{5}+3 &=2 y \\ \frac{x^{5}+3}{2} &=y \end{aligned}\)
替代\(f^{-1}(x)\)\(y\)。
\(f^{-1}(x)=\frac{x^{5}+3}{2}\)
验证函数是否为反向函数。
\(\begin{array}{rr} {f^{-1}(f(x)) \stackrel{?}{=} x} & {f\left(f^{-1}(x)\right) \stackrel{?}{=} x} \\ {f^{-1}(\sqrt[5]{2x-3})\stackrel{?}{=}x}&{f\left(\frac{x^{5}+3}{2} \right)}\stackrel{?}{=}x \\ {\frac{(\sqrt[5]{2x-3})^{5}+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{2\left(\frac{x^{5}+3}{2} \right)-3}\stackrel{?}{=}x} \\ {\frac{2x-3+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}+3-3}\stackrel{?}{=}x}\\ {\frac{2x}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}}\stackrel{?}{=}x} \\ {x=x}&{x=x} \end{array}\)
找出函数的逆函数\(f(x)=\sqrt[5]{3 x-2}\)。
- 回答
-
\(f^{-1}(x)=\frac{x^{5}+2}{3}\)
找出函数的逆函数\(f(x)=\sqrt[4]{6 x-7}\)。
- 回答
-
\(f^{-1}(x)=\frac{x^{4}+7}{6}\)
关键概念
- 函数的构成:函数\(f\)和\(g\),由以下人员编写\(f∘g\)和定义
\((f \circ g)(x)=f(g(x))\)
\(f(g(x))\)截至目前,我们\(f\)已\(g\)阅读\(x\)。 - 水平线测试:如果每条水平线与函数的图形最多相交一个点,则它是一对一的函数。
- 由有序对定义的函数的逆函数:如果\(f(x)\)是一个一对一的函数,其有序对的形式为\((x,y)\),则其逆函数\(f^{−1}(x)\)是有序对的集合\((y,x)\)。
- 反函数:对于一对一函数域\(x\)中的每一个函数\(f\)\(f^{−1}\),
\(f^{-1}(f(x))=x\)
\(f\left(f^{-1}(x)\right)=x\) - 如何找到一对一函数的逆函数:
- 替代\(y\)\(f(x)\)。
- 交换变量\(x\)和\(y\)。
- 求解\(y\)。
- 替代\(f^{−1}(x)\)\(y\)。
- 验证函数是否为反向函数。
词汇表
- 一对一功能
- 如果范围中的每个值在域中只有一个元素,则函数为一对一。 对于函数中的每个有序对,每个\(y\)-value 仅与一个\(x\)-value 匹配。


