8.9E：练习

练习成就完美

练习 1-4：计算负数的平方根

在以下练习中，按顺序编写每个表达式，\(i\)并尽可能简化。

1. a.\(\sqrt{-16}\) b.\(\sqrt{-11}\) c.\(\sqrt{-8}\)
2. a.\(\sqrt{-121}\) b.\(\sqrt{-1}\) c.\(\sqrt{-20}\)
3. a.\(\sqrt{-100}\) b.\(\sqrt{-13}\) c.\(\sqrt{-45}\)
4. a.\(\sqrt{-49}\) b.\(\sqrt{-15}\) c.\(\sqrt{-75}\)

回答

1. a.\(4i\) b.\(i\sqrt{11}\) c.\(2i\sqrt{2}\)

3. a.\(10i\) b.\(i\sqrt{13}\) c.\(3i\sqrt{5}\)

练习 5-21：加上或减去复数

在以下练习中，加上或减去，将答案\(a + bi\)写成表格。

5。 \(\sqrt{-75}+\sqrt{-48}\)

6。 \(\sqrt{-12}+\sqrt{-75}\)

7。 \(\sqrt{-50}+\sqrt{-18}\)

8。 \(\sqrt{-72}+\sqrt{-8}\)

9。 \((1+3 i)+(7+4 i)\)

10。 \((6+2 i)+(3-4 i)\)

11。 \((8-i)+(6+3 i)\)

12。 \((7-4 i)+(-2-6 i)\)

13。 \((1-4 i)-(3-6 i)\)

14。 \((8-4 i)-(3+7 i)\)

15。 \((6+i)-(-2-4 i)\)

16。 \((-2+5 i)-(-5+6 i)\)

17。 \((5-\sqrt{-36})+(2-\sqrt{-49})\)

18。 \((-3+\sqrt{-64})+(5-\sqrt{-16})\)

19。 \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)

20。 \((-5+\sqrt{-27})-(-4-\sqrt{-48})\)

回答

5。 \(0+\left(9\sqrt{3}\right)i\)

7。 \(0+\left(8\sqrt{2}\right)i\)

9。 \(8+7i\)

11。 \(14+2i\)

13。 \(-2+2i\)

15。 \(8+5i\)

17。 \(7-13i\)

19。 \(25-\left(2 \sqrt{2}\right) i\)

练习 21-28：将复数相乘

在以下练习中，乘以，将答案\(a+bi\)写成表格。

21。 \(4 i(5-3 i)\)

22。 \(2 i(-3+4 i)\)

23。 \(-6 i(-3-2 i)\)

24。 \(-i(6+5 i)\)

25。 \((4+3 i)(-5+6 i)\)

26。 \((-2-5 i)(-4+3 i)\)

27。 \((-3+3 i)(-2-7 i)\)

28。 \((-6-2 i)(-3-5 i)\)

回答

21。 \(12+20i\)

23。 \(-12+18i\)

25。 \(-38+9 i\)

27。 \(27+15i\)

练习 29-32：将复数相乘

在以下练习中，使用二项式方块的乘积图案进行乘法，将答案变为\(a+bi\)形式。

29。 \((3+4 i)^{2}\)

30。 \((-1+5 i)^{2}\)

31。 \((-2-3 i)^{2}\)

32。 \((-6-5 i)^{2}\)

回答

29。 \(-7+24i\)

31。 \(-5-12i\)

练习 33-46：将复数相乘

在以下练习中，乘以，将答案\(a+bi\)写成表格。

33。 \(\sqrt{-25} \cdot \sqrt{-36}\)

34。 \(\sqrt{-4} \cdot \sqrt{-16}\)

35。 \(\sqrt{-9} \cdot \sqrt{-100}\)

36。 \(\sqrt{-64} \cdot \sqrt{-9}\)

37。 \((-2-\sqrt{-27})(4-\sqrt{-48})\)

38。 \((5-\sqrt{-12})(-3+\sqrt{-75})\)

39。 \((2+\sqrt{-8})(-4+\sqrt{-18})\)

40。 \((5+\sqrt{-18})(-2-\sqrt{-50})\)

41。 \((2-i)(2+i)\)

42。 \((4-5 i)(4+5 i)\)

43。 \((7-2 i)(7+2 i)\)

44。 \((-3-8 i)(-3+8 i)\)

回答

33。 \(30i = 0 + 30i\)

35。 \(-30 = -30 + 0i\)

37。 \(-44+\left(4 \sqrt{3}\right) i\)

39。 \(-20-\left(2 \sqrt{2}\right) i\)

41。 \(5 = 5 + 0i\)

43。 \(53 = 53 + 0i\)

练习 45-49：将复数相乘

在以下练习中，使用复杂共轭物乘积图案进行乘法。

45。 \((7-i)(7+i)\)

46。 \((6-5 i)(6+5 i)\)

47。 \((9-2 i)(9+2 i)\)

48。 \((-3-4 i)(-3+4 i)\)

回答

45。 \(50\)

47。 \(85\)

练习 49-60：除以复数

在以下练习中，划分，将答案\(a+bi\)写成表格。

49。 \(\dfrac{3+4 i}{4-3 i}\)

50。 \(\dfrac{5-2 i}{2+5 i}\)

51。 \(\dfrac{2+i}{3-4 i}\)

52。 \(\dfrac{3-2 i}{6+i}\)

53。 \(\dfrac{3}{2-3 i}\)

54。 \(\dfrac{2}{4-5 i}\)

55。 \(\dfrac{-4}{3-2 i}\)

56。 \(\dfrac{-1}{3+2 i}\)

57。 \(\dfrac{1+4 i}{3 i}\)

58。 \(\dfrac{4+3 i}{7 i}\)

59。 \(\dfrac{-2-3 i}{4 i}\)

60。 \(\dfrac{-3-5 i}{2 i}\)

回答

49。 \(i = 0 + i\)

51。 \(\frac{2}{25}+\frac{11}{25} i\)

53。 \(\frac{6}{13}+\frac{9}{13} i\)

55。 \(-\frac{12}{13}-\frac{8}{13} i\)

57。 \(\frac{4}{3}-\frac{1}{3} i\)

59。 \(-\frac{3}{4}+\frac{1}{2} i\)

练习 61-68：简化力量\(i\)

在以下练习中，进行简化。

61。 \(i^{41}\)

62。 \(i^{39}\)

63。 \(i^{66}\)

64。 \(i^{48}\)

65。 \(i^{128}\)

66。 \(i^{162}\)

67。 \(i^{137}\)

68。 \(i^{255}\)

回答

61。 \(i^{41} = i^{40}\cdot i = \left(i^{4}\right)^{10}\cdot i= i\)

63。 \(i^{66} = i^{64}\cdot i^{2} = \left(i^{4}\right)^{16}\cdot (-1)= -1\)

65。 \(i^{128} = \left(i^{4}\right)^{32} = 1\)

67。 \(i^{137} = i^{136}\cdot i = \left(i^{4}\right)^{34}\cdot i = 1 \cdot i = i\)

练习 69-72：写作练习

69。 解释实数和复数之间的关系。

70。 Aniket乘法如下，他得到了错误的答案。 他的推理有什么问题？
\(\begin{array}{c}{\sqrt{-7} \cdot \sqrt{-7}} \\ {\sqrt{49}} \\ {7}\end{array}\)

71。 为什么是，\(\sqrt{-64}=8 i\)但是\(\sqrt[3]{-64}=-4\).

72。 解释除以复数与合理化分母有何相似。

回答

69。 答案可能有所不同

71。 答案可能有所不同

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

图 8.8.15

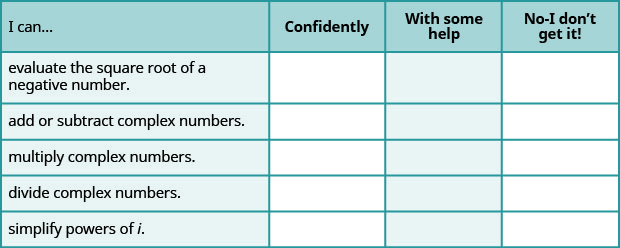
b. 在 1-10 分中，根据你在清单上的回答，你会如何评价你对本节的掌握程度？ 你怎么能改善这个？