8.9: 使用复数系统
- Page ID
- 204016
在本节结束时,您将能够:
- 计算负数的平方根
- 相加和减去复数
- 将复数相乘
- 除以复数
- 简化权力\(i\)
在开始之前,请参加这个准备测验。
- 给定数字\(-4,-\sqrt{7}, 0 . \overline{5}, \frac{7}{3}, 3, \sqrt{81}\),列出
- 有理数
- 非理性数字
- 实数
如果你错过了这个问题,请查看示例 1.42。
- 乘以:\((x−3)(2x+5)\)。
如果您错过了此问题,请查看示例 5.28。 - 合理化分母:\(\frac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}\)
如果你错过了这个问题,请查看示例 5.32。
计算负数的平方根
每当我们遇到负数平方根的情况时,我们都说没有实数等于该平方根。 例如,为了简化起见\(\sqrt{-1}\),我们正在寻找一个\(x\)实数\(x^{2}=-1\)。 由于所有实数的平方都是正数,因此在平方\(–1\)时没有等于的实数。
数学家经常根据需要扩展他们的数字系统。 他们\(0\)将计数数字相加得出整数。 当他们需要负余额时,他们会添加负数来获得整数。 当他们需要整体各部分的概念时,他们会添加分数并得到有理数。 将非理性数字相加允许使用诸如\(\sqrt{5}\). 所有这些共同给了我们实数,到目前为止,在你对数学的研究中,这已经足够了。
但是现在我们将扩展实数以包括负数的平方根。 我们首先将虚数单位定义\(i\)为平方为的数字\(–1\)。
定义\(\PageIndex{1}\)
虚数单位\(i\)是平方为的数字\(-1\)。
\(i^{2}=-1 \text { or } i=\sqrt{-1}\)
我们将使用虚数单位来简化负数的平方根。
定义\(\PageIndex{2}\)
负数的平方根
如果\(b\)是正实数,那么
\(\sqrt{-b}=\sqrt{b} i\)
我们将在下一个示例中使用这个定义。 请注意,很明显,激进分子\(i\)不在激进之下。 有时候你会看到这篇文章\(\sqrt{-b}=i \sqrt{b}\)是为了强调不在\(i\)激进之下。 但是\(\sqrt{-b}=\sqrt{b} i\)它被认为是标准形式。
按顺序写下每个表达式\(i\),简化是可能的:
- \(\sqrt{-25}\)
- \(\sqrt{-7}\)
- \(\sqrt{-12}\)
解决方案:
一个。
\(\sqrt{-25}\)
使用负数平方根的定义。
\(\sqrt{25} i\)
简化。
\(5i\)
b。
\(\sqrt{-7}\)
使用负数平方根的定义。
\(\sqrt{7} i\)
简化。
请注意,这显然\(i\)不是激进的迹象。
c。
\(\sqrt{-12}\)
使用负数平方根的定义。
\(\sqrt{12} i\)
简化\(\sqrt{12}\)。
\(2 \sqrt{3} i\)
按顺序编写每个表达式\(i\),并尽可能简化:
- \(\sqrt{-81}\)
- \(\sqrt{-5}\)
- \(\sqrt{-18}\)
- 回答
-
- \(9i\)
- \(\sqrt{5} i\)
- \(3 \sqrt{2} i\)
按顺序编写每个表达式\(i\),并尽可能简化:
- \(\sqrt{-36}\)
- \(\sqrt{-3}\)
- \(\sqrt{-27}\)
- 回答
-
- \(6i\)
- \(\sqrt{3} i\)
- \(3\sqrt{3} i\)
现在我们已经熟悉虚数了\(i\),我们可以扩展实数以包括虚数。 复数系统包括实数和虚数。 复数的形式为\(a+bi\),其中\(a, b\)是实数。 我们称\(a\)之为真实\(b\)部分和虚部。
定义\(\PageIndex{3}\)
复数的形式为\(a+bi\),其中\(a\)和\(b\)是实数。
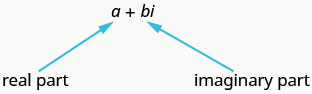
复数在写成、其中\(a+bi\)\(a\)、为实数时采用标准形式。\(b\)
if\(b=0\),然后\(a+bi\)变成\(a+0⋅i=a\),并且是一个实数。
if\(b≠0\),\(a+bi\)then 是一个虚数。
i\(a=0\) f,则\(a+bi\)变成\(0+bi=bi\),并被称为纯虚数。
我们在这里总结一下。
| \(a+bi\) | ||
| \(b=0\) |
\(a+0 \cdot i\) \(a\) |
实数 |
| \(b\neq 0\) | \(a+bi\) | 虚数 |
| \(a=0\)R |
\(0+bi\) \(bi\) |
纯虚数4 |
复数的标准形式是\(a+bi\),所以这就解释了为什么首选形式是\(\sqrt{-b}=\sqrt{b} i\)时间\(b>0\)。
该图帮助我们可视化复数系统。 它由实数和虚数组成。
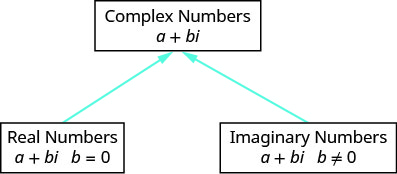
加上或减去复数
我们现在可以对复数执行加法、减法、乘法和除法运算了,就像我们对待实数一样。
相加和减去复数很像将项相加或减去。 我们加上或减去实部,然后加上或减去虚部。 我们的最终结果应该是标准形式。
添加:\(\sqrt{-12}+\sqrt{-27}\)。
解决方案:
\(\sqrt{-12}+\sqrt{-27}\)
使用负数平方根的定义。
\(\sqrt{12} i+\sqrt{27} i\)
简化平方根。
\(2 \sqrt{3} i+3 \sqrt{3} i\)
添加。
\(5 \sqrt{3} i\)
添加:\(\sqrt{-8}+\sqrt{-32}\)。
- 回答
-
\(6 \sqrt{2} i\)
添加:\(\sqrt{-27}+\sqrt{-48}\)
- 回答
-
\(7 \sqrt{3} i\)
记得在下一个示例中将实数部分和虚部相加。
简化:
- \((4-3 i)+(5+6 i)\)
- \((2-5 i)-(5-2 i)\)
解决方案:
一个。
\((4-3 i)+(5+6 i)\)
使用关联属性将实部和虚部放在一起。
\((4+5)+(-3 i+6 i)\)
简化。
\(9+3i\)
b。
\((2-5 i)-(5-2 i)\)
分发。
\(2-5 i-5+2 i\)
使用关联属性将实部和虚部放在一起。
\(2-5-5 i+2 i\)
简化。
\(-3-3 i\)
简化:
- \((2+7 i)+(4-2 i)\)
- \((8-4 i)-(2-i)\)
- 回答
-
- \(6+5i\)
- \(6-3i\)
简化:
- \((3-2 i)+(-5-4 i)\)
- \((4+3 i)-(2-6 i)\)
- 回答
-
- \(-2-6i\)
- \(2+9i\)
将复数相乘
将复数相乘也很像将表达式与系数和变量相乘。 我们只需要考虑一个特殊情况。 我们将在接下来的两个示例中练习之后再看一下。
乘以:\(2 i(7-5 i)\)
解决方案:
\(2 i(7-5 i)\)
分发。
\(14 i-10 i^{2}\)
简化\(i^{2}\)。
\(14 i-10(-1)\)
乘以。
\(14 i+10\)
以标准形式书写。
\(10+14i\)
乘以:\(4 i(5-3 i)\)。
- 回答
-
\(12+20i\)
乘以:\(-3 i(2+4 i)\)。
- 回答
-
\(12-6i\)
在下一个示例中,我们使用分布属性或 FOIL 将二项式相乘。
乘以:\((3+2 i)(4-3 i)\)。
解决方案:
\((3+2 i)(4-3 i)\)
使用铝箔。
\(12-9 i+8 i-6 i^{2}\)
简\(i^{2}\)化和合并相似的术语。
\(12-i-6(-1)\)
乘以。
\(12-i+6\)
将真实部分组合在一起。
\(18-i\)
多个:\((5-3 i)(-1-2 i)\)。
- 回答
-
\(-11-7i\)
多个:\((-4-3 i)(2+i)\)。
- 回答
-
\(-5-10i\)
在下一个示例中,我们可以使用 F OIL 或二项式方块乘积图案。
乘以:\((3+2 i)^{2}\)
解决方案:
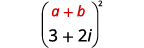 |
|
| 使用二项式正方形图案的乘积,\((a+b)^{2}=a^{2}+2 a b+b^{2}\)。 |  |
| 简化。 | 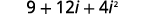 |
| 简化\(i^{2}\)。 | 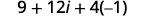 |
| 简化。 | 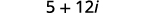 |
使用二项式正方形图案进行乘法:\((-2-5 i)^{2}\).
- 回答
-
\(-21+20 i\)
使用二项式正方形图案进行乘法:\((-5+4 i)^{2}\).
- 回答
-
\(9-40i\)
由于负数的平方根不是实数,因此我们不能使用基数的乘积属性。 为了将负数的平方根相乘,我们应该首先将它们写成复数,使用\(\sqrt{-b}=\sqrt{b}i\) .This 是学生容易出错的地方,所以当你看到乘以负平方根时要小心。
乘以:\(\sqrt{-36} \cdot \sqrt{-4}\)。
解决方案:
要将负数的平方根相乘,我们首先将它们写成复数。
\(\sqrt{-36} \cdot \sqrt{-4}\)
使用作为复数写入\(\sqrt{-b}=\sqrt{b}i\)。
\(\sqrt{36} i \cdot \sqrt{4} i\)
简化。
\(6 i \cdot 2 i\)
乘以。
\(12i^{2}\)
简化\(i^{2}\)并乘以。
\(-12\)
乘以:\(\sqrt{-49} \cdot \sqrt{-4}\)。
- 回答
-
\(-14\)
乘以:\(\sqrt{-36} \cdot \sqrt{-81}\)。
- 回答
-
\(-54\)
在下一个示例中,每个二项式都有一个负数的平方根。 在乘法之前,必须将负数的每个平方根写成复数。
乘以:\((3-\sqrt{-12})(5+\sqrt{-27})\)。
解决方案:
要将负数的平方根相乘,我们首先将它们写成复数。
\((3-\sqrt{-12})(5+\sqrt{-27})\)
使用作为复数写入\(\sqrt{-b}=\sqrt{b}i\)。
\((3-2 \sqrt{3} i)(5+3 \sqrt{3} i)\)
使用铝箔。
\(15+9 \sqrt{3} i-10 \sqrt{3} i-6 \cdot 3 i^{2}\)
合并相似的术语并进行简化\(i^{2}\)。
\(15-\sqrt{3} i-6 \cdot(-3)\)
相似的项相乘和合并。
\(33-\sqrt{3} i\)
乘以:\((4-\sqrt{-12})(3-\sqrt{-48})\)。
- 回答
-
\(-12-22 \sqrt{3} i\)
乘以:\((-2+\sqrt{-8})(3-\sqrt{-18})\)。
- 回答
-
\(6+12 \sqrt{2} i\)
我们在研究多项式时首先研究了共轭对。 我们说过,一对二项式的第一个项和最后一个项相同,但一个是总和,一个是差值,被称为共轭对,其形式是这样\((a−b),(a+b)\)。
复杂的共轭对非常相似。 对于形式的复数\(a+bi\),其共轭为\(a−bi\)。 请注意,它们的第一个项和最后一个项相同,但是一个是总和,一个是差值。
定义\(\PageIndex{4}\)
复杂共轭对的形式为\(a+bi,a-bi\)。
在下一个示例中,我们将乘以一个复数共轭对。
乘以:\((3-2 i)(3+2 i)\)。
解决方案:
\((3-2 i)(3+2 i)\)
使用铝箔
\(9+6 i-6 i-4 i^{2}\)
合并相似的术语并进行简化\(i^{2}\)。
\(9-4(-1)\)
相似的项相乘和合并。
\(13\)
乘以:\((4-3 i) \cdot(4+3 i)\)。
- 回答
-
\(25\)
乘以:\((-2+5 i) \cdot(-2-5 i)\)。
- 回答
-
\(29\)
根据我们对多项式的研究,我们知道共轭物的乘积始终是\((a-b)(a+b)=a^{2}-b^{2}\)这种形式。结果称为平方差。 我们可以使用这个模式乘以一个复杂的共轭对。
最后一个例子我们使用了 FOIL。 现在我们将使用共轭乘积模式。
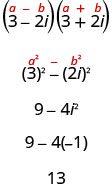
请注意,这与我们在示例 8.8.9 中找到的结果相同。
当我们将复数共轭物相乘时,最后一项的乘积将始终\(i^{2}\)具有简化为\(−1\)。
\(\begin{array}{c}{(a-b i)(a+b i)} \\ {a^{2}-(b i)^{2}} \\ {a^{2}-b^{2} i^{2}} \\ {a^{2}-b^{2}(-1)} \\ {a^{2}+b^{2}}\end{array}\)
这使我们得出了复杂共轭物模式的乘积:\((a-b i)(a+b i)=a^{2}+b^{2}\)
定义\(\PageIndex{5}\)
复合偶联物的乘积
如果\(a\)和\(b\)是实数,那么
\((a-b i)(a+b i)=a^{2}+b^{2}\)
使用复杂共轭物模式的乘积进行乘法:\((8-2 i)(8+2 i)\).
解决方案:
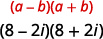 |
|
| 使用复杂共轭物图案的乘积,\((a-b i)(a+b i)=a^{2}+b^{2}\)。 | 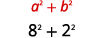 |
| 简化方块。 | 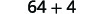 |
| 添加。 | 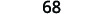 |
使用复杂共轭物模式的乘积进行乘法:\((3-10 i)(3+10 i)\).
- 回答
-
\(109\)
使用复杂共轭物模式的乘积进行乘法:\((-5+4 i)(-5-4 i)\).
- 回答
-
\(41\)
除以复数
除以复数很像合理化分母。 我们希望结果采用标准形式,分母中没有虚数。
除以:\(\frac{4+3 i}{3-4 i}\)。
解决方案:
| 步骤 1:用标准形式写下分子和分母。 | 它们都是标准形式。 | \(\frac{4+3 i}{3-4 i}\) |
| 步骤 2:将分子和分母乘以分母的复共轭。 | 的复共轭\(3-4i\)是\(3+4i\)。 | \(\frac{(4+3 i)\color{red}{(3+4 i)}}{(3-4 i)\color{red}{(3+4 i)}}\) |
| 第 3 步:简化结果并将其写入标准格式。 |
使用分母\((a-b i)(a+b i)=a^{2}+b^{2}\)中的图案。 将相似的术语组合在一起。 简化。 以标准形式写出结果。 |
\(\begin{array}{c}{\frac{12+16 i+9 i+12 i^{2}}{9+16}} \\ {\frac{12+25 i-12}{25}} \\ {\frac{25 i}{25}} \\ {i}\end{array}\) |
除以:\(\frac{2+5 i}{5-2 i}\)。
- 回答
-
\(i\)
除以:\(\frac{1+6 i}{6-i}\)。
- 回答
-
\(i\)
我们在这里总结一下步骤。
如何除以复数
- 用标准形式写下分子和分母。
- 将分子和分母乘以分母的复共轭。
- 简化结果并将其写入标准格式。
划分,以标准形式写出答案:\(\frac{-3}{5+2 i}\)。
解决方案:
\(\frac{-3}{5+2 i}\)
将分子和分母乘以分母的复共轭。
\(\frac{-3(5-2 i)}{(5+2 i)(5-2 i)}\)
将分子相乘,然后在分母中使用复共轭模式的乘积。
\(\frac{-15+6 i}{5^{2}+2^{2}}\)
简化。
\(\frac{-15+6 i}{29}\)
以标准形式书写。
\(-\frac{15}{29}+\frac{6}{29} i\)
除以,用标准形式写出答案:\(\frac{4}{1-4 i}\)。
- 回答
-
\(\frac{4}{17}+\frac{16}{17} i\)
除以,用标准形式写出答案:\(\frac{-2}{-1+2 i}\)。
- 回答
-
\(\frac{2}{5}+\frac{4}{5} i\)
在找到分母的共轭时要小心。
除以:\(\frac{5+3 i}{4 i}\)。
解决方案:
\(\frac{5+3 i}{4 i}\)
用标准形式写下分母。
\(\frac{5+3 i}{0+4 i}\)
将分子和分母乘以分母的复共轭。
\(\frac{(5+3 i)(0-4 i)}{(0+4 i)(0-4 i)}\)
简化。
\(\frac{(5+3 i)(-4 i)}{(4 i)(-4 i)}\)
乘以。
\(\frac{-20 i-12 i^{2}}{-16 i^{2}}\)。
简化\(i^{2}\).
\(\frac{-20 i+12}{16}\)
以标准形式重写。
\(\frac{12}{16}-\frac{20}{16} i\)
简化分数。
\(\frac{3}{4}-\frac{5}{4} i\)
除以:\(\frac{3+3 i}{2 i}\)。
- 回答
-
\(\frac{3}{2}-\frac{3}{2} i\)
除以:\(\frac{2+4 i}{5 i}\)。
- 回答
-
\(\frac{4}{5}-\frac{2}{5} i\)
简化 Power of\(i\)
\(i\)制作有趣模式的力量将帮助我们简化更高的功率\(i\)。 让我们评估一下的功\(i\)率以查看模式。
\(\begin{array}{ccc}{i^{1}} & {i^{2}} & {i^{3}} & {i^{4}} \\ {i} & {-1} & {i^{2}\cdot i} & {i^{2}\cdot i^{2}}\\ {}&{}&{-1\cdot i}&{(-1)(-1)}\\ {}&{}&{-i}&{1}\end{array}\)
\(\begin{array}{cccc}{i^{5}} & {i^{6}} & {i^{7}} & {i^{8}} \\ {i^{4} \cdot i} & {i^{4} \cdot i^{2}} & {i^{4} \cdot i^{3}} & {i^{4} \cdot i^{4}} \\ {1 \cdot i} & {1 \cdot i^{2}} & {1 \cdot i^{3}} & {1 \cdot 1} \\ {i} & {i^{2}} & {i^{3}} & {1} \\ {}&{-1} & {-i}\end{array}\)
我们现在总结一下。
\(\begin{array}{ll}{i^{1}=i} & {i^{5}=i} \\ {i^{2}=-1} & {i^{6}=-1} \\ {i^{3}=-i} & {i^{7}=-i} \\ {i^{4}=1} & {i^{8}=1}\end{array}\)
如果我们继续下去,这种模式将继续以四组为单位重复。 我们可以使用这种模式来帮助我们简化功能\(i\)。 从那以后\(i^{4}=1\),我们将每个 power 重写为一个乘积\(i^{n}\),再\(i^{4}\)将另一个功率改为 power\(i\)。
我们用以下形式重写它\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\)\(q\),其中指数是\(n\)除以的商\(r\),\(4\)而指数是该除法的余数。 例如,为了简化起\(i^{57}\)见,我们\(57\)除\(4\)以,然后得\(14\)出余数\(1\)。 换句话说,\(57=4⋅14+1\)。 所以我们编写\(i^{57}=\left(1^{4}\right)^{14} \cdot i^{1}\)然后从那里进行简化。
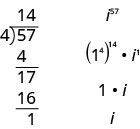
简化:\(i^{86}\)。
解决方案:
\(i^{86}\)
除\(86\)以\(4\),然后在\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\)表单\(i^{86}\)中重写。
\(\left(1^{4}\right)^{21} \cdot i^{2}\)
简化。
\((1)^{21} \cdot(-1)\)
简化。
\(-1\)
简化:\(i^{74}\)。
- 回答
-
\(-1\)
简化:\(i^{92}\)。
- 回答
-
\(1\)
访问这些在线资源,获取有关复数系统的更多指导和练习。
- 用 i 表示负数的平方根
- 减去和乘以复数
- 除以复数
- 重写 i 的力量
关键概念
- 负数的平方根
- 如果\(b\)是正实数,那么\ (\ sqrt {-b} =\ sqrt {b} i\
| \(a+bi\) | ||
| \(b=0\) |
\(a+0\cdot i\) \(a\) |
实数 |
| \(b\neq 0\) | \(a+bi\) | 虚数 |
| \(a=0\) |
\(0+bi\) \(bi\) |
纯虚数 |
-
- 复数写成 a + bi 时采用标准形式,其中 a, b 是实数。
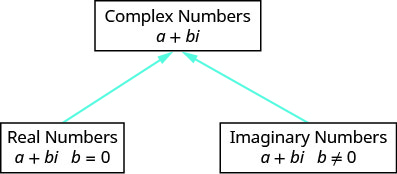
图 8.8.2
- 复数写成 a + bi 时采用标准形式,其中 a, b 是实数。
- 复合偶联物的乘积
- 如果\(a, b\)是实数,那么
\((a−bi)(a+bi)=a^{2}+b^{2}\)
- 如果\(a, b\)是实数,那么
- 如何除以复数
- 用标准形式写下分子和分母。
- 将分子和分母乘以分母的复共轭。
- 简化结果并将其写入标准格式。
词汇表
- 复数共轭对
- 复杂共轭对的形式为\(a+bi, a-bi\)。
- 复数
- 复数的形式为\(a+bi\),其中\(a\)和\(b\)是实数。 我们称\(a\)之为真实\(b\)部分和虚部。
- 复数系统
- 复数系统由实数和虚数组成。
- 虚数单位
- 虚数单位\(i\)是平方为的数字\(–1\)。 \(i^{2}=-1\)或\(i=\sqrt{−1}\)。
- 标准表单
- 复数写成时采用标准形式\(a+bi\),其中\(a, b\)是实数。


