8.8E：练习

Last updated

Nov 1, 2022
Page ID
203974
Save as PDF
- 8.8: 在函数中使用自由基
- 8.9: 使用复数系统

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

练习成就完美

练习 $\PageIndex{17}$ Evaluate a Radical Function

在以下练习中，评估每个函数。

$f(x)=\sqrt{4 x-4}$ ，找到
1. $f(5)$
2. $f(0)$
$f(x)=\sqrt{6 x-5}$ ，找到
1. $f(5)$
2. $f(-1)$
$g(x)=\sqrt{6 x+1}$ ，找到
1. $g(4)$
2. $g(8)$
$g(x)=\sqrt{3 x+1}$ ，找到
1. $g(8)$
2. $g(5)$
$F(x)=\sqrt{3-2 x}$ ，找到
1. $F(1)$
2. $F(-11)$
$F(x)=\sqrt{8-4 x}$ ，找到
1. $F(1)$
2. $F(-2)$
$G(x)=\sqrt{5 x-1}$ ，找到
1. $G(5)$
2. $G(2)$
$G(x)=\sqrt{4 x+1}$ ，找到
1. $G(11)$
2. $G(2)$
$g(x)=\sqrt[3]{2 x-4}$ ，找到
1. $g(6)$
2. $g(-2)$
$g(x)=\sqrt[3]{7 x-1}$ ，找到
1. $g(4)$
2. $g(-1)$
$h(x)=\sqrt[3]{x^{2}-4}$ ，找到
1. $h(-2)$
2. $h(6)$
$h(x)=\sqrt[3]{x^{2}+4}$ ，找到
1. $h(-2)$
2. $h(6)$
对于该函数 $f(x)=\sqrt[4]{2 x^{3}}$ ，请找到
1. $f(0)$
2. $f(2)$
对于该函数 $f(x)=\sqrt[4]{3 x^{3}}$ ，请找到
1. $f(0)$
2. $f(3)$
对于该函数 $g(x)=\sqrt[4]{4-4 x}$ ，请找到
1. $g(1)$
2. $g(-3)$
对于该函数 $g(x)=\sqrt[4]{8-4 x}$ ，请找到
1. $g(-6)$
2. $g(2)$

回答

1。

$f(5)=4$
此处没有价值 $x=0$

3。

$g(4)=5$
$g(8)=7$

5。

$F(1)=1$
$F(-11)=5$

7。

$G(5)=2 \sqrt{6}$
$G(2)=3$

9。

$g(6)=2$
$g(-2)=-2$

11。

$h(-2)=0$
$h(6)=2 \sqrt[3]{4}$

13。

$f(0)=0$
$f(2)=2$

15。

$g(1)=0$
$g(-3)=2$

练习 $\PageIndex{18}$ Find the Domain of a Radical Function

在以下练习中，找到函数的域，然后用区间表示法写下该域。

$f(x)=\sqrt{3 x-1}$
$f(x)=\sqrt{4 x-2}$
$g(x)=\sqrt{2-3 x}$
$g(x)=\sqrt{8-x}$
$h(x)=\sqrt{\frac{5}{x-2}}$
$h(x)=\sqrt{\frac{6}{x+3}}$
$f(x)=\sqrt{\frac{x+3}{x-2}}$
$f(x)=\sqrt{\frac{x-1}{x+4}}$
$g(x)=\sqrt[3]{8 x-1}$
$g(x)=\sqrt[3]{6 x+5}$
$f(x)=\sqrt[3]{4 x^{2}-16}$
$f(x)=\sqrt[3]{6 x^{2}-25}$
$F(x)=\sqrt[4]{8 x+3}$
$F(x)=\sqrt[4]{10-7 x}$
$G(x)=\sqrt[5]{2 x-1}$
$G(x)=\sqrt[5]{6 x-3}$

回答

1。 $\left[\frac{1}{3}, \infty\right)$

3。 $\left(-\infty, \frac{2}{3}\right]$

5。 $(2, \infty)$

7。 $(-\infty,-3] \cup(2, \infty)$

9。 $(-\infty, \infty)$

11。 $(-\infty, \infty)$

13。 $\left[-\frac{3}{8}, \infty\right)$

15。 $(-\infty, \infty)$

练习 $\PageIndex{19}$ graph radical functions

在以下练习中，

找到函数的域
绘制函数图
使用图表确定范围
1. $f(x)=\sqrt{x+1}$
2. $f(x)=\sqrt{x-1}$
3. $g(x)=\sqrt{x+4}$
4. $g(x)=\sqrt{x-4}$
5. $f(x)=\sqrt{x}+2$
6. $f(x)=\sqrt{x}-2$
7. $g(x)=2 \sqrt{x}$
8. $g(x)=3 \sqrt{x}$
9. $f(x)=\sqrt{3-x}$
10. $f(x)=\sqrt{4-x}$
11. $g(x)=-\sqrt{x}$
12. $g(x)=-\sqrt{x}+1$
13. $f(x)=\sqrt[3]{x+1}$
14. $f(x)=\sqrt[3]{x-1}$
15. $g(x)=\sqrt[3]{x+2}$
16. $g(x)=\sqrt[3]{x-2}$
17. $f(x)=\sqrt[3]{x}+3$
18. $f(x)=\sqrt[3]{x}-3$
19. $g(x)=\sqrt[3]{x}$
20. $g(x)=-\sqrt[3]{x}$
21. $f(x)=2 \sqrt[3]{x}$
22. $f(x)=-2 \sqrt[3]{x}$

回答

1。

域: $[-1, \infty)$
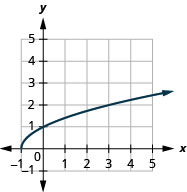
$该图显示了 x y 坐标平面上的平方根函数图。平面的 x 轴从负 1 延伸到 7。 y 轴从负 2 延伸到 10。该函数的起点为（负 1, 0），并穿过两个点 (0, 1) 和 (3, 2)。$
图 8.7.8
$[0, \infty)$

3。

域: $[-4, \infty)$
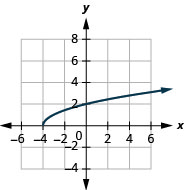
$该图显示了 x y 坐标平面上的平方根函数图。飞机的 x 轴从负 4 延伸到 4。 y 轴从负 2 延伸到 6。该函数的起点为（负 4, 0），并穿过两个点（负 3, 1）和（0, 2）。$
图 8.7.9
$[0, \infty)$

5。

域: $[0, \infty)$
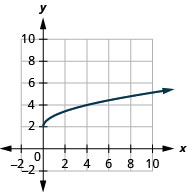
$该图显示了 x y 坐标平面上的平方根函数图。飞机的 x 轴从 0 到 8 延伸。 y 轴从 0 到 8 延伸。该函数的起点为 (0, 2)，并穿过点 (1, 3) 和 (4, 4)。$
图 8.7.10
$[2, \infty)$

7。

域: $[0, \infty)$
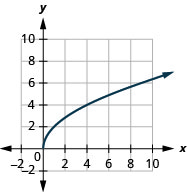
$该图显示了 x y 坐标平面上的平方根函数图。飞机的 x 轴从 0 到 8 延伸。 y 轴从 0 到 8 延伸。该函数的起点为 (0, 0)，并穿过点 (1, 2) 和 (4, 4)。$
图 8.7.11
$[0, \infty)$

9。

域: $(-\infty, 3]$
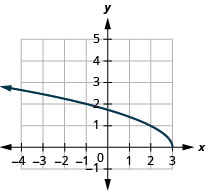
$该图显示了 x y 坐标平面上的平方根函数图。飞机的 x 轴从负 6 延伸到 4。 y 轴从 0 到 8 延伸。该函数的起点为 (3, 0)，穿过点 (2, 1)、(负 1、2) 和 (负 6、3)。$
图 8.7.12
$[0, \infty)$

11。

域: $[0, \infty)$
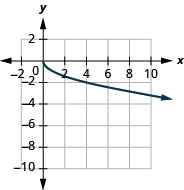
$该图显示了 x y 坐标平面上的平方根函数图。飞机的 x 轴从 0 到 8 延伸。 y 轴从负 8 到 0 延伸。该函数的起点为 (0, 0)，并穿过点 (1，负 1) 和 (4，负 2)。$
图 8.7.13
$(-\infty, 0]$

13。

域: $(-\infty, \infty)$
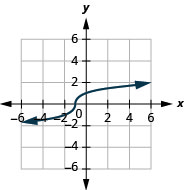
$该图显示了 x y 坐标平面上的立方根函数图。飞机的 x 轴从负 4 延伸到 4。 y 轴从负 4 延伸到 4。该函数的中心点位于（负 1, 0）并穿过各点（负 2、负 1）和（0, 1）。$
图 8.7.14
$(-\infty, \infty)$

15。

域: $(-\infty, \infty)$
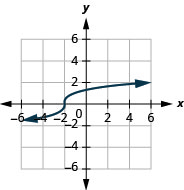
$该图显示了 x y 坐标平面上的立方根函数图。飞机的 x 轴从负 4 延伸到 4。 y 轴从负 4 延伸到 4。该函数的中心点位于（负 4, 0）并穿过各点（负 3、负 1）和（负 1、1）。$
图 8.7.15
$(-\infty, \infty)$

17。

域: $(-\infty, \infty)$
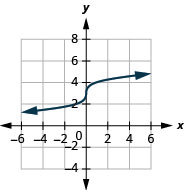
$该图显示了 x y 坐标平面上的立方根函数图。飞机的 x 轴从负 4 延伸到 4。 y 轴从负 2 延伸到 6。该函数的中心点位于 (0, 3) 并穿过这些点 (负 1, 2) 和 (1, 4)。$
图 8.7.16
$(-\infty, \infty)$

19。

域: $(-\infty, \infty)$
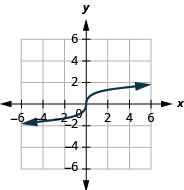
$该图显示了 x y 坐标平面上的立方根函数图。飞机的 x 轴从负 4 延伸到 4。 y 轴从负 4 延伸到 4。该函数的中心点位于 (0, 0) 并穿过点 (1, 1) 和 (负 1, 负 1)。$
图 8.7.17
$(-\infty, \infty)$

21。

域: $(-\infty, \infty)$
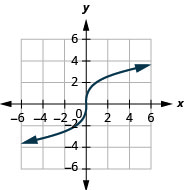
$该图显示了 x y 坐标平面上的立方根函数图。飞机的 x 轴从负 4 延伸到 4。 y 轴从负 4 延伸到 4。该函数的中心点位于 (0, 0) 并穿过点 (1, 2) 和 (负 1, 负 2)。$
图 8.7.18
$(-\infty, \infty)$

练习 $\PageIndex{20}$ writing exercises

解释如何找到第四个根函数的域。
解释如何找到第五个根函数的域。
解释为什么 $y=\sqrt[3]{x}$ 是函数。
解释为什么查找具有偶数索引的激进函数的域的过程与索引为奇数时的过程不同。

回答

1。答案可能有所不同

3。答案可能有所不同

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

该表有 4 列和 4 行。第一行是标题行，标题为 “我可以”、“confidently¿ €”、“有帮助。” 还有 “不行”，还有 “我不明白！™ £€。第一列包含短语 “评估激进函数”、“找到激进函数的域” 和 “绘制激进函数”。其他栏留空，以便学员可以表明自己的理解水平。 — 图 8.7.19

b. 关于你对本部分的掌握程度，这份清单告诉了你什么？你会采取哪些措施来改进？

练习成就完美

练习17\PageIndex{17} Evaluate a Radical Function

练习18\PageIndex{18} Find the Domain of a Radical Function

练习19\PageIndex{19} graph radical functions

练习20\PageIndex{20} writing exercises

自检

练习 $\PageIndex{17}$ Evaluate a Radical Function

练习 $\PageIndex{18}$ Find the Domain of a Radical Function

练习 $\PageIndex{19}$ graph radical functions

练习 $\PageIndex{20}$ writing exercises