8.8: 在函数中使用自由基
- Page ID
- 203964
在本节结束时,您将能够:
- 评估激进函数
- 找到激进函数的域
- 图表激进函数
在开始之前,请参加这个准备测验。
- 解决:\(1−2x≥0\)。
如果你错过了这个问题,请查看示例 2.50。 - 对于\(f(x)=3x−4\),评估\(f(2),f(−1),f(0)\)。
如果您错过了此问题,请查看示例 3.48。 - 图表\(f(x)=\sqrt{x}\)。 用区间表示法陈述函数的域和范围。
如果你错过了这个问题,请查看示例 3.56。
评估激进函数
在本节中,我们将扩展我们之前的函数研究范围,将激进分子包括在内。 如果一个函数是由激进表达式定义的,我们称之为激进函数。
- 平方根函数是\(f(x)=\sqrt{x}\)。
- 立方根函数是\(f(x)=\sqrt[3]{x}\)。
激进函数是由激进表达式定义的函数。
为了评估激进函数,我们发现给定值的值为,\(x\)就像我们在之前使用函数时所做的那样。\(f(x)\)
对于该函数\(f(x)=\sqrt{2 x-1}\),请找到
- \(f(5)\)
- \(f(-2)\)
解决方案:
一个。
\(f(x)=\sqrt{2 x-1}\)
要进行评估\(f(5)\),请\(5\)替换\(x\)。
\(f(5)=\sqrt{2 \cdot 5-1}\)
简化。
\(f(5)=\sqrt{9}\)
取平方根。
\(f(5)=3\)
b。
\(f(x)=\sqrt{2 x-1}\)
要进行评估\(f(-2)\),请\(-2\)替换\(x\)。
\(f(-2)=\sqrt{2(-2)-1}\)
简化。
\(f(-2)=\sqrt{-5}\)
由于负数的平方根不是实数,因此该函数的值不在\(x=-2\)。
对于该函数\(f(x)=\sqrt{3 x-2}\),请找到
- \(f(6)\)
- \(f(0)\)
- 回答
-
- \(f(6)=4\)
- 此处没有价值\(x=0\)
对于该函数\(g(x)=\sqrt{5x+5}\),请找到
- \(g(4)\)
- \(g(-3)\)
- 回答
-
- \(g(4)=5\)
- 此处没有价值\(f(-3)\)
我们按照相同的程序来评估立方根值。
对于该函数\(g(x)=\sqrt[3]{x-6}\),请找到
- \(g(14)\)
- \(g(-2)\)
解决方案:
一个。
\(g(x)=\sqrt[3]{x-6}\)
要进行评估\(g(14)\),请\(14\)替换\(x\)。
\(g(14)=\sqrt[3]{14-6}\)
简化。
\(g(14)=\sqrt[3]{8}\)
取立方体根。
\(g(14)=2\)
b。
\(g(x)=\sqrt[3]{x-6}\)
要进行评估\(g(-2)\),请\(-2\)替换\(x\)。
\(g(-2)=\sqrt[3]{-2-6}\)
简化。
\(g(-2)=\sqrt[3]{-8}\)
取立方体根。
\(g(-2)=-2\)
对于该函数\(g(x)=\sqrt[3]{3 x-4}\),请找到
- \(g(4)\)
- \(g(1)\)
- 回答
-
- \(g(4)=2\)
- \(g(1)=-1\)
对于该函数\(h(x)=\sqrt[3]{5 x-2}\),请找到
- \(h(2)\)
- \(h(-5)\)
- 回答
-
- \(h(2)=2\)
- \(h(-5)=-3\)
下一个例子有第四个根源。
对于该函数\(f(x)=\sqrt[4]{5 x-4}\),请找到
- \(f(4)\)
- \(f(-12)\)
解决方案:
一个。
\(f(x)=\sqrt[4]{5 x-4}\)
要进行评估\(f(4)\),请\(4\)替换\(x\)。
\(f(4)=\sqrt[4]{5 \cdot 4-4}\)
简化。
\(f(4)=\sqrt[4]{16}\)
取第四根根。
\(f(4)=2\)
b。
\(f(x)=\sqrt[4]{5 x-4}\)
要进行评估\(f(-12)\),请\(-12\)替换\(x\)。
\(f(-12)=\sqrt[4]{5(-12)-4}\)
简化。
\(f(-12)=\sqrt[4]{-64}\)
由于负数的第四个根不是实数,因此该函数的值不在\(x=-12\)。
对于该函数\(f(x)=\sqrt[4]{3 x+4}\),请找到
- \(f(4)\)
- \(f(-1)\)
- 回答
-
- \(f(4)=2\)
- \(f(-1)=1\)
对于该函数\(g(x)=\sqrt[4]{5 x+1}\),请找到
- \(g(16)\)
- \(g(3)\)
- 回答
-
- \(g(16)=3\)
- \(g(3)=2\)
找到激进函数的域
为了找到自由基函数的域和范围,我们使用自由基的特性。 对于指数为偶数的激进,我们说激进数必须大于或等于零,因为即使是负数的根也不是实数。 对于奇数索引,基数可以是任何实数。 我们在这里重述这些属性以供参考。
的属性\(\sqrt[n]{a}\)
什么时候\(n\)是偶数,并且:
- \(a \geq 0\),则\(\sqrt[n]{a}\)是一个实数。
- \(a<0\),\(\sqrt[n]{a}\)则不是实数。
如果\(n\)是奇数,\(\sqrt[n]{a}\)则是所有值的实数\(a\)。
因此,为了找到具有偶数索引的激进函数的域,我们将基数设置为大于或等于零。 对于奇数索引部首,基数可以是任何实数。
自由基函数的域
当激进的索引为偶数时,基数必须大于或等于零。
当激进的索引为奇数时,radicand 可以是任何实数。
找到函数的域,\(f(x)=\sqrt{3 x-4}\)。 用间隔表示法写下域。
解决方案:
由于函数\(f(x)=\sqrt{3 x-4}\)有一个索引为偶数的基数\(2\),因此我们知道基数必须大于或等于\(0\)。 我们将 radicand 设置为大于或等于,\(0\)然后求解以找到该域。
解决。
\(\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}\)
的域\(f(x)=\sqrt{3 x-4}\)是所有值\(x \geq \frac{4}{3}\),我们用间隔表示法将其写成\(\left[\frac{4}{3}, \infty\right)\)。
找到函数的域,\(f(x)=\sqrt{6 x-5}\)。 用间隔表示法写下域。
- 回答
-
\(\left[\frac{5}{6}, \infty\right)\)
找到函数的域,\(f(x)=\sqrt{4-5 x}\)。 用间隔表示法写下域。
- 回答
-
\(\left(-\infty, \frac{4}{5}\right]\)
找到函数的域,\(g(x)=\sqrt{\frac{6}{x-1}}\)。 用间隔表示法写下域。
解决方案:
求解函数,\(g(x)=\sqrt{\frac{6}{x-1}}\)有一个索引为偶数的\(2\)基数,我们知道 radicand 必须大于或等于\(0\)。
由于分子不为零,因此基数不能为零。
\(\frac{6}{x-1}\)要大于零,则分母必须为正,因为分子为正。 我们知道正数除以正数是正数。
我们设置\(x-1>0\)并解决。
\(x-1>0\)
解决。
\(x>1\)
另外,由于基数是一个分数,我们必须意识到分母不能为零。
我们下\(x-1=0\)定决心找到必须从域中消除的值。
\(x-1=0\)
解决。
\(x=1\)所以\(x/neq 1\)在域中。
把这个放在一起,我们就得到域名是\(x>1\),我们把它写成\((1, \infty)\)。
找到函数的域,\(f(x)=\sqrt{\frac{4}{x+3}}\)。 用间隔表示法写下域。
- 回答
-
\((-3, \infty)\)
找到函数的域,\(h(x)=\sqrt{\frac{9}{x-5}}\)。 用间隔表示法写下域。
- 回答
-
\((5, \infty)\)
下一个例子涉及立方根,因此需要不同的思考。
找到函数的域,\(f(x)=\sqrt[3]{2 x^{2}+3}\)。 用间隔表示法写下域。
解决方案:
由于函数\(f(x)=\sqrt[3]{2 x^{2}+3}\)有一个索引为奇数的基数\(3\),因此我们知道 radicand 可以是任何实数。 这告诉我们域名是任何实数。 用间隔表示法,我们写\((-\infty, \infty)\)。
的域\(f(x)=\sqrt[3]{2 x^{2}+3}\)都是实数,我们用间隔表示法将其写成\((-\infty, \infty)\)。
找到函数的域,\(f(x)=\sqrt[3]{3 x^{2}-1}\)。 用间隔表示法写下域。
- 回答
-
\((-\infty, \infty)\)
找到函数的域,\(g(x)=\sqrt[3]{5 x-4}\)。 用间隔表示法写下域。
- 回答
-
\((-\infty, \infty)\)
图表激进函数
在我们绘制任何激进函数的图形之前,我们首先要找到该函数的域。 对于函数\(f(x)=\sqrt{x}\),索引为偶数,因此基数必须大于或等于\(0\)。
这告诉我们域是\(x≥0\),我们用间隔表示法将其写成\([0,∞)\)。
之前我们使用点图来绘制函数的图形\(f(x)=\sqrt{x}\)。 我们选择了\(x\)-values,将它们替换成了,然后创建了一个图表。 请注意,我们选择完美正方形的点是为了更轻松地计算平方根。
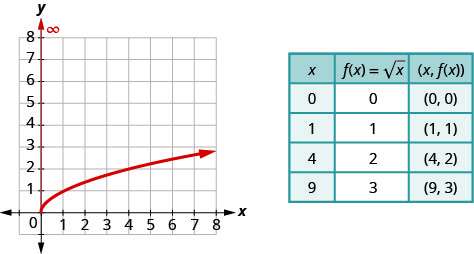
看到图表后,我们就能找到函数的范围。 函数的\(y\)-values 大于或等于零。 那么范围是\([0,∞)\)。
对于这个函数\(f(x)=\sqrt{x+3}\),
- 找到域名
- 绘制函数图
- 使用图表确定范围
解决方案:
- 由于激进有索引\(2\),我们知道基数必须大于或等于零。 如果\(x+3 \geq 0\),那么\(x \geq-3\)。 这告诉我们域是所有值\(x \geq-3\),用间隔表示法写成\([-3, \infty)\)。
- 为了绘制函数的图形,我们在区间中选择点\([-3, \infty)\),这些点也会给出一个很容易取平方根的基数。
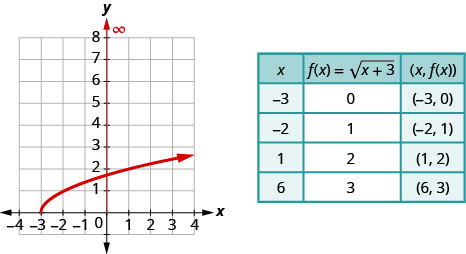
c. 从图表中可以看出,函数的\(y\)-values 大于或等于零。 那么范围是\([0, \infty)\)。
对于这个函数\(f(x)=\sqrt{x+2}\),
- 找到域名
- 绘制函数图
- 使用图表确定范围
- 回答
-
- 域:\([-2, \infty)\)
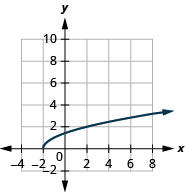
图 8.7.3- 范围:\([0, \infty)\)
对于这个函数\(f(x)=\sqrt{x-2}\),
- 找到域名
- 绘制函数图
- 使用图表确定范围
- 回答
-
- 域:\([2, \infty)\)
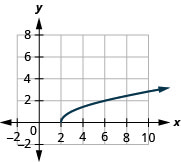
图 8.7.4- 范围:\([0, \infty)\)
在我们之前的绘制函数的工作中,我们绘制了图形,\(f(x)=x^{3}\)但没有绘制函数图\(f(x)=\sqrt[3]{x}\)。 我们现在将在下一个示例中执行此操作。
对于该函数\(f(x)=\sqrt[3]{x}\),
- 找到域名
- 绘制函数图
- 使用图表确定范围
解决方案:
a. 既然激进有索引\(3\),我们知道激进分子可以是任何实数。 这告诉我们域都是实数,用间隔表示法写成\((-\infty, \infty)\)
b. 为了绘制函数的图形,我们在区间中选择点\((-\infty, \infty)\),这也会给我们一个基数,它很容易取立方根。

c. 从图表中可以看出,\(y\)函数的-values 都是实数。 那么范围是\((-\infty, \infty)\)。
对于这个函数\(f(x)=-\sqrt[3]{x}\),
- 找到域名
- 绘制函数图
- 使用图表确定范围
- 回答
-
- 域:\((-\infty, \infty)\)
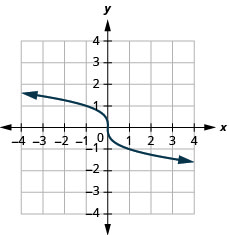
图 8.7.6- 范围:\((-\infty, \infty)\)
对于这个函数\(f(x)=\sqrt[3]{x-2}\),
- 找到域名
- 绘制函数图
- 使用图表确定范围
- 回答
-
- 域:\((-\infty, \infty)\)
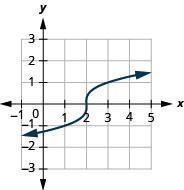
图 8.7.7- 范围:\((-\infty, \infty)\)
访问这些在线资源,获取更多指导和使用激进功能进行练习。
- 自由基函数的域
- 自由基函数域 2
- 寻找激进函数的域
关键概念
- 的属性\(\sqrt[n]{a}\)
- W\(n\) hen 是偶数
\(a≥0\),而:则\(\sqrt[n]{a}\)是实数。
\(a<0\),\(\sqrt[n]{a}\)则不是实数。 - 如果\(n\)是奇数,\(\sqrt[n]{a}\)则是所有值的实数\(a\)。
- W\(n\) hen 是偶数
- 自由基函数的域
- 当激进的索引为偶数时,基数必须大于或等于零。
- 当激进的索引为奇数时,radicand 可以是任何实数。
词汇表
- 激进函数
- 激进函数是由激进表达式定义的函数。


