Skip to main content
Global

第 8 章复习练习

  1. Last updated
  2. Save as PDF
  • Page ID
    204044

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    章节复习练习

    使用根简化表达式

    练习\(\PageIndex{1}\) Simplify Expressions with Roots

    在以下练习中，简化。

      1. \(\sqrt{225}\)
      2. \(-\sqrt{16}\)
      1. \(-\sqrt{169}\)
      2. \(\sqrt{-8}\)
      1. \(\sqrt[3]{8}\)
      2. \(\sqrt[4]{81}\)
      3. \(\sqrt[5]{243}\)
      1. \(\sqrt[3]{-512}\)
      2. \(\sqrt[4]{-81}\)
      3. \(\sqrt[5]{-1}\)
    回答

    1。

    1. \(15\)
    2. \(-4\)

    3。

    1. \(2\)
    2. \(3\)
    3. \(3\)
    练习\(\PageIndex{2}\) Estimate and Approximate Roots

    在以下练习中，估计两个连续整数之间的每个根。

      1. \(\sqrt{68}\)
      2. \(\sqrt[3]{84}\)
    回答

    1。

    1. \(8<\sqrt{68}<9\)
    2. \(4<\sqrt[3]{84}<5\)
    练习\(\PageIndex{3}\) Estimate and Approximate Roots

    在以下练习中，近似每个根并四舍五入到小数点后两位。

      1. \(\sqrt{37}\)
      2. \(\sqrt[3]{84}\)
      3. \(\sqrt[4]{125}\)
    回答

    1。 自己解决

    练习\(\PageIndex{4}\) Simplify Variable Expressions with Roots

    在以下练习中，根据需要简化绝对值的使用。

      1. \(\sqrt[3]{a^{3}}\)
      2. \(\sqrt[7]{b^{7}}\)
      1. \(\sqrt{a^{14}}\)
      2. \(\sqrt{w^{24}}\)
      1. \(\sqrt[4]{m^{8}}\)
      2. \(\sqrt[5]{n^{20}}\)
      1. \(\sqrt{121 m^{20}}\)
      2. \(-\sqrt{64 a^{2}}\)
      1. \(\sqrt[3]{216 a^{6}}\)
      2. \(\sqrt[5]{32 b^{20}}\)
      1. \(\sqrt{144 x^{2} y^{2}}\)
      2. \(\sqrt{169 w^{8} y^{10}}\)
      3. \(\sqrt[3]{8 a^{51} b^{6}}\)
    回答

    1。

    1. \(a\)
    2. \(|b|\)

    3。

    1. \(m^{2}\)
    2. \(n^{4}\)

    5。

    1. \(6a^{2}\)
    2. \(2b^{4}\)

    简化激进表达式

    练习\(\PageIndex{5}\) Use the Product Property to Simplify Radical Expressions

    在以下练习中，使用产品属性来简化激进表达式。

    1. \(\sqrt{125}\)
    2. \(\sqrt{675}\)
      1. \(\sqrt[3]{625}\)
      2. \(\sqrt[6]{128}\)
    回答

    1。 \(5\sqrt{5}\)

    3。

    1. \(5 \sqrt[3]{5}\)
    2. \(2 \sqrt[6]{2}\)
    练习\(\PageIndex{6}\) Use the Product Property to Simplify Radical Expressions

    在以下练习中，根据需要简化绝对值符号的使用。

      1. \(\sqrt{a^{23}}\)
      2. \(\sqrt[3]{b^{8}}\)
      3. \(\sqrt[8]{c^{13}}\)
      1. \(\sqrt{80 s^{15}}\)
      2. \(\sqrt[5]{96 a^{7}}\)
      3. \(\sqrt[6]{128 b^{7}}\)
      1. \(\sqrt{96 r^{3} s^{3}}\)
      2. \(\sqrt[3]{80 x^{7} y^{6}}\)
      3. \(\sqrt[4]{80 x^{8} y^{9}}\)
      1. \(\sqrt[5]{-32}\)
      2. \(\sqrt[8]{-1}\)
      1. \(8+\sqrt{96}\)
      2. \(\frac{2+\sqrt{40}}{2}\)
    回答

    2。

    1. \(4\left|s^{7}\right| \sqrt{5 s}\)
    2. \(2 a \sqrt[5]{3 a^{2}}\)
    3. \(2|b| \sqrt[6]{2 b}\)

    4。

    1. \(-2\)
    2. 不是真的
    练习\(\PageIndex{7}\) Use the Quotient Property to Simplify Radical Expressions

    在以下练习中，使用 Quotient 属性简化平方根。

      1. \(\sqrt{\frac{72}{98}}\)
      2. \(\sqrt[3]{\frac{24}{81}}\)
      3. \(\sqrt[4]{\frac{6}{96}}\)
      1. \(\sqrt{\frac{y^{4}}{y^{8}}}\)
      2. \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
      3. \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
    3. \(\sqrt{\frac{300 m^{5}}{64}}\)
      1. \(\sqrt{\frac{28 p^{7}}{q^{2}}}\)
      2. \(\sqrt[3]{\frac{81 s^{8}}{t^{3}}}\)
      3. \(\sqrt[4]{\frac{64 p^{15}}{q^{12}}}\)
      1. \(\sqrt{\frac{27 p^{2} q}{108 p^{4} q^{3}}}\)
      2. \(\sqrt[3]{\frac{16 c^{5} d^{7}}{250 c^{2} d^{2}}}\)
      3. \(\sqrt[6]{\frac{2 m^{9} n^{7}}{128 m^{3} n}}\)
      1. \(\frac{\sqrt{80 q^{5}}}{\sqrt{5 q}}\)
      2. \(\frac{\sqrt[3]{-625}}{\sqrt[3]{5}}\)
      3. \(\frac{\sqrt[4]{80 m^{7}}}{\sqrt[4]{5 m}}\)
    回答

    1。

    1. \(\frac{6}{7}\)
    2. \(\frac{2}{3}\)
    3. \(\frac{1}{2}\)

    3。 \(\frac{10 m^{2} \sqrt{3 m}}{8}\)

    5。

    1. \(\frac{1}{2|p q|}\)
    2. \(\frac{2 c d \sqrt[5]{2 d^{2}}}{5}\)
    3. \(\frac{|m n| \sqrt[6]{2}}{2}\)

    简化有理指数

    练习\(\PageIndex{8}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    在以下练习中，写成激进表达式。

      1. \(r^{\frac{1}{2}}\)
      2. \(s^{\frac{1}{3}}\)
      3. \(t^{\frac{1}{4}}\)
    回答

    1。

    1. \(\sqrt{r}\)
    2. \(\sqrt[3]{s}\)
    3. \(\sqrt[4]{t}\)
    练习\(\PageIndex{9}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    在以下练习中，用有理指数书写。

      1. \(\sqrt{21p}\)
      2. \(\sqrt[4]{8q}\)
      3. \(4\sqrt[6]{36r}\)
    回答

    1。 自己解决

    练习\(\PageIndex{10}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    在以下练习中，简化。

      1. \(625^{\frac{1}{4}}\)
      2. \(243^{\frac{1}{5}}\)
      3. \(32^{\frac{1}{5}}\)
      1. \((-1,000)^{\frac{1}{3}}\)
      2. \(-1,000^{\frac{1}{3}}\)
      3. \((1,000)^{-\frac{1}{3}}\)
      1. \((-32)^{\frac{1}{5}}\)
      2. \((243)^{-\frac{1}{5}}\)
      3. \(-125^{\frac{1}{3}}\)
    回答

    1。

    1. \(5\)
    2. \(3\)
    3. \(2\)

    3。

    1. \(-2\)
    2. \(\frac{1}{3}\)
    3. \(-5\)
    练习\(\PageIndex{11}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    在以下练习中，用有理指数书写。

      1. \(\sqrt[4]{r^{7}}\)
      2. \((\sqrt[5]{2 p q})^{3}\)
      3. \(\sqrt[4]{\left(\frac{12 m}{7 n}\right)^{3}}\)
    回答

    1。 自己解决

    练习\(\PageIndex{12}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    在以下练习中，简化。

      1. \(25^{\frac{3}{2}}\)
      2. \(9^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{2}{3}}\)
      1. \(-64^{\frac{3}{2}}\)
      2. \(-64^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{3}{2}}\)
    回答

    1。

    1. \(125\)
    2. \(\frac{1}{27}\)
    3. \(16\)
    练习\(\PageIndex{13}\) Use the Laws of Exponents to Simplify Expressions with Rational Exponents

    在以下练习中，简化。

      1. \(6^{\frac{5}{2}} \cdot 6^{\frac{1}{2}}\)
      2. \(\left(b^{15}\right)^{\frac{3}{5}}\)
      3. \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
      1. \(\frac{a^{\frac{3}{4}} \cdot a^{-\frac{1}{4}}}{a^{-\frac{10}{4}}}\)
      2. \(\left(\frac{27 b^{\frac{2}{3}} c^{-\frac{5}{2}}}{b^{-\frac{7}{3}} c^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    回答

    1。

    1. \(6^{3}\)
    2. \(b^{9}\)
    3. \(\frac{1}{w}\)

    加、减和乘以激进表达式

    练习\(\PageIndex{14}\) add and Subtract Radical Expressions

    在以下练习中，简化。

      1. \(7 \sqrt{2}-3 \sqrt{2}\)
      2. \(7 \sqrt[3]{p}+2 \sqrt[3]{p}\)
      3. \(5 \sqrt[3]{x}-3 \sqrt[3]{x}\)
      1. \(\sqrt{11 b}-5 \sqrt{11 b}+3 \sqrt{11 b}\)
      2. \(8 \sqrt[4]{11 c d}+5 \sqrt[4]{11 c d}-9 \sqrt[4]{11 c d}\)
      1. \(\sqrt{48}+\sqrt{27}\)
      2. \(\sqrt[3]{54}+\sqrt[3]{128}\)
      3. \(6 \sqrt[4]{5}-\frac{3}{2} \sqrt[4]{320}\)
      1. \(\sqrt{80 c^{7}}-\sqrt{20 c^{7}}\)
      2. \(2 \sqrt[4]{162 r^{10}}+4 \sqrt[4]{32 r^{10}}\)
    5. \(3 \sqrt{75 y^{2}}+8 y \sqrt{48}-\sqrt{300 y^{2}}\)
    回答

    1。

    1. \(4\sqrt{2}\)
    2. \(9\sqrt[3]{p}\)
    3. \(2\sqrt[3]{x}\)

    3。

    1. \(7\sqrt{3}\)
    2. \(7\sqrt[3]{2}\)
    3. \(3\sqrt[4]{5}\)

    5。 \(37 y \sqrt{3}\)

    练习\(\PageIndex{15}\) Multiply Radical Expressions

    在以下练习中，简化。

      1. \((5 \sqrt{6})(-\sqrt{12})\)
      2. \((-2 \sqrt[4]{18})(-\sqrt[4]{9})\)
      1. \(\left(3 \sqrt{2 x^{3}}\right)\left(7 \sqrt{18 x^{2}}\right)\)
      2. \(\left(-6 \sqrt[3]{20 a^{2}}\right)\left(-2 \sqrt[3]{16 a^{3}}\right)\)
    回答

    2。

    1. \(126 x^{2} \sqrt{2}\)
    2. \(48 a \sqrt[3]{a^{2}}\)
    练习\(\PageIndex{16}\) Use Polynomial Multiplication to Multiply Radical Expressions

    在以下练习中，乘以。

      1. \(\sqrt{11}(8+4 \sqrt{11})\)
      2. \(\sqrt[3]{3}(\sqrt[3]{9}+\sqrt[3]{18})\)
      1. \((3-2 \sqrt{7})(5-4 \sqrt{7})\)
      2. \((\sqrt[3]{x}-5)(\sqrt[3]{x}-3)\)
    3. \((2 \sqrt{7}-5 \sqrt{11})(4 \sqrt{7}+9 \sqrt{11})\)
      1. \((4+\sqrt{11})^{2}\)
      2. \((3-2 \sqrt{5})^{2}\)
    5. \((7+\sqrt{10})(7-\sqrt{10})\)
    6. \((\sqrt[3]{3 x}+2)(\sqrt[3]{3 x}-2)\)
    回答

    2。

    1. \(71-22 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-8 \sqrt[3]{x}+15\)

    4。

    1. \(27+8 \sqrt{11}\)
    2. \(29-12 \sqrt{5}\)

    6。 \(\sqrt[3]{9 x^{2}}-4\)

    划分激进表达式

    练习\(\PageIndex{17}\) Divide Square Roots

    在以下练习中，简化。

      1. \(\frac{\sqrt{48}}{\sqrt{75}}\)
      2. \(\frac{\sqrt[3]{81}}{\sqrt[3]{24}}\)
      1. \(\frac{\sqrt{320 m n^{-5}}}{\sqrt{45 m^{-7} n^{3}}}\)
      2. \(\frac{\sqrt[3]{16 x^{4} y^{-2}}}{\sqrt[3]{-54 x^{-2} y^{4}}}\)
    回答

    2。

    1. \(\frac{8 m^{4}}{3 n^{4}}\)
    2. \(-\frac{x^{2}}{2 y^{2}}\)
    练习\(\PageIndex{18}\) rationalize a One Term Denominator

    在以下练习中，合理化分母。

      1. \(\frac{8}{\sqrt{3}}\)
      2. \(\sqrt{\frac{7}{40}}\)
      3. \(\frac{8}{\sqrt{2 y}}\)
      1. \(\frac{1}{\sqrt[3]{11}}\)
      2. \(\sqrt[3]{\frac{7}{54}}\)
      3. \(\frac{3}{\sqrt[3]{3 x^{2}}}\)
      1. \(\frac{1}{\sqrt[4]{4}}\)
      2. \(\sqrt[4]{\frac{9}{32}}\)
      3. \(\frac{6}{\sqrt[4]{9 x^{3}}}\)
    回答

    2。

    1. \(\frac{\sqrt[3]{121}}{11}\)
    2. \(\frac{\sqrt[3]{28}}{6}\)
    3. \(\frac{\sqrt[3]{9 x}}{x}\)
    练习\(\PageIndex{19}\) Rationalize a Two Term Denominator

    在以下练习中，简化。

    1. \(\frac{7}{2-\sqrt{6}}\)
    2. \(\frac{\sqrt{5}}{\sqrt{n}-\sqrt{7}}\)
    3. \(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}-\sqrt{8}}\)
    回答

    1。 \(-\frac{7(2+\sqrt{6})}{2}\)

    3。 \(\frac{(\sqrt{x}+2 \sqrt{2})^{2}}{x-8}\)

    求解激进方程

    练习\(\PageIndex{20}\) Solve Radical Equations

    在以下练习中，求解。

    1. \(\sqrt{4 x-3}=7\)
    2. \(\sqrt{5 x+1}=-3\)
    3. \(\sqrt[3]{4 x-1}=3\)
    4. \(\sqrt{u-3}+3=u\)
    5. \(\sqrt[3]{4 x+5}-2=-5\)
    6. \((8 x+5)^{\frac{1}{3}}+2=-1\)
    7. \(\sqrt{y+4}-y+2=0\)
    8. \(2 \sqrt{8 r+1}-8=2\)
    回答

    2. 没有解决办法

    4。 \(u=3, u=4\)

    6。 \(x=-4\)

    8。 \(r=3\)

    练习\(\PageIndex{21}\) Solve Radical Equations with Two Radicals

    在以下练习中，求解。

    1. \(\sqrt{10+2 c}=\sqrt{4 c+16}\)
    2. \(\sqrt[3]{2 x^{2}+9 x-18}=\sqrt[3]{x^{2}+3 x-2}\)
    3. \(\sqrt{r}+6=\sqrt{r+8}\)
    4. \(\sqrt{x+1}-\sqrt{x-2}=1\)
    回答

    2。 \(x=-8, x=2\)

    4。 \(x=3\)

    练习\(\PageIndex{22}\) Use Radicals in Applications

    在以下练习中，求解。 将近似值四舍五入到小数点后一位。

    1. 园林绿化 Reed 想在他的后院有一块方形的花园。 他有足够的堆肥来覆盖一\(75\)平方英尺的面积。 使用公式\(s=\sqrt{A}\)求出他花园两边的长度。 将答案四舍五入到最接近的十分之一英尺。
    2. 事故调查一名事故调查员测量了其中一辆发生事故的车辆的防滑痕迹。 防滑痕迹的长度为\(175\)英尺。 在施加制动之前，使用该公式\(s=\sqrt{24d}\)找出车辆的速度。 将答案四舍五入到最接近的十分之一。
    回答

    2。 \(64.8\)英尺

    在函数中使用自由基

    练习\(\PageIndex{23}\) Evaluate a Radical Function

    在以下练习中，评估每个函数。

    1. \(g(x)=\sqrt{6 x+1}\)，找到
      1. \(g(4)\)
      2. \(g(8)\)
    2. \(G(x)=\sqrt{5 x-1}\)，找到
      1. \(G(5)\)
      2. \(G(2)\)
    3. \(h(x)=\sqrt[3]{x^{2}-4}\)，找到
      1. \(h(-2)\)
      2. \(h(6)\)
    4. 对于该函数\(g(x)=\sqrt[4]{4-4 x}\)，请找到
      1. \(g(1)\)
      2. \(g(-3)\)
    回答

    2。

    1. \(G(5)=2 \sqrt{6}\)
    2. \(G(2)=3\)

    4。

    1. \(g(1)=0\)
    2. \(g(-3)=2\)
    练习\(\PageIndex{24}\) Find the Domain of a Radical Function

    在以下练习中，找到函数的域，然后用区间表示法写下该域。

    1. \(g(x)=\sqrt{2-3 x}\)
    2. \(F(x)=\sqrt{\frac{x+3}{x-2}}\)
    3. \(f(x)=\sqrt[3]{4 x^{2}-16}\)
    4. \(F(x)=\sqrt[4]{10-7 x}\)
    回答

    2。 \((2, \infty)\)

    4。 \(\left[\frac{7}{10}, \infty\right)\)

    练习\(\PageIndex{25}\) graph Radical Functions

    在以下练习中，

    1. 找到函数的域
    2. 绘制函数图
    3. 使用图表确定范围
    1. \(g(x)=\sqrt{x+4}\)
    2. \(g(x)=2 \sqrt{x}\)
    3. \(f(x)=\sqrt[3]{x-1}\)
    4. \(f(x)=\sqrt[3]{x}+3\)
    回答

    2。

    1. 域:\([0, \infty)\)

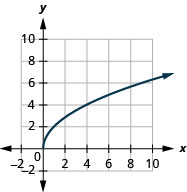
    2. 该图显示了 x y 坐标平面上的平方根函数图。 飞机的 x 轴从 0 到 8 延伸。 y 轴从 0 到 8 延伸。 该函数的起点为 (0, 0)，并穿过点 (1, 2) 和 (4, 4)。
      图 8.E.1
    3. 范围：\([0, \infty)\)

    4。

    1. 域:\((-\infty, \infty)\)

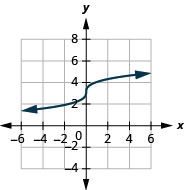
    2. 该图显示了 x y 坐标平面上的立方根函数图。 飞机的 x 轴从负 4 延伸到 4。 y 轴从负 2 延伸到 6。 该函数的中心点位于 (0, 3) 并穿过这些点 (负 1, 2) 和 (1, 4)。
      图 8.E.2
    3. 范围：\((-\infty, \infty)\)

    使用复数系统

    练习\(\PageIndex{26}\) evaluate the Square Root of a Negative Number

    在以下练习中，按顺序编写每个表达式，\(i\)并尽可能简化。

      1. \(\sqrt{-100}\)
      2. \(\sqrt{-13}\)
      3. \(\sqrt{-45}\)
    回答

    自己解决

    练习\(\PageIndex{27}\) Add or Subtract Complex Numbers

    在以下练习中，加或减。

    1. \(\sqrt{-50}+\sqrt{-18}\)
    2. \((8-i)+(6+3 i)\)
    3. \((6+i)-(-2-4 i)\)
    4. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)
    回答

    1。 \(8 \sqrt{2} i\)

    3。 \(8+5 i\)

    练习\(\PageIndex{28}\) Multiply Complex Numbers

    在以下练习中，乘以。

    1. \((-2-5 i)(-4+3 i)\)
    2. \(-6 i(-3-2 i)\)
    3. \(\sqrt{-4} \cdot \sqrt{-16}\)
    4. \((5-\sqrt{-12})(-3+\sqrt{-75})\)
    回答

    1。 \(23+14 i\)

    3。 \(-6\)

    练习\(\PageIndex{29}\) Multiply Complex Numbers

    在以下练习中，使用二项式方块的乘积图案进行乘法。

    1. \((-2-3 i)^{2}\)
    回答

    1。 \(-5-12 i\)

    练习\(\PageIndex{30}\) Multiply Complex Numbers

    在以下练习中，使用复杂共轭物乘积图案进行乘法。

    1. \((9-2 i)(9+2 i)\)
    回答

    自己解决

    练习\(\PageIndex{31}\) divide Complex Numbers

    在以下练习中，除以。

    1. \(\frac{2+i}{3-4 i}\)
    2. \(\frac{-4}{3-2 i}\)
    回答

    1。 \(\frac{2}{25}+\frac{11}{25} i\)

    练习\(\PageIndex{32}\) Simplify Powers of \(i\)

    在以下练习中，简化。

    1. \(i^{48}\)
    2. \(i^{255}\)
    回答

    1。 \(1\)

    练习测试

    练习\(\PageIndex{33}\)

    在以下练习中，根据需要简化绝对值的使用。

    1. \(\sqrt[3]{125 x^{9}}\)
    2. \(\sqrt{169 x^{8} y^{6}}\)
    3. \(\sqrt[3]{72 x^{8} y^{4}}\)
    4. \(\sqrt{\frac{45 x^{3} y^{4}}{180 x^{5} y^{2}}}\)
    回答

    1。 \(5x^{3}\)

    3。 \(2 x^{2} y \sqrt[3]{9 x^{2} y}\)

    练习\(\PageIndex{34}\)

    在以下练习中，简化。 假设所有变量均为正。

      1. \(216^{-\frac{1}{4}}\)
      2. \(-49^{\frac{3}{2}}\)
    2. \(\sqrt{-45}\)
    3. \(\frac{x^{-\frac{1}{4}} \cdot x^{\frac{5}{4}}}{x^{-\frac{3}{4}}}\)
    4. \(\left(\frac{8 x^{\frac{2}{3}} y^{-\frac{5}{2}}}{x^{-\frac{7}{3}} y^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    5. \(\sqrt{48 x^{5}}-\sqrt{75 x^{5}}\)
    6. \(\sqrt{27 x^{2}}-4 x \sqrt{12}+\sqrt{108 x^{2}}\)
    7. \(2 \sqrt{12 x^{5}} \cdot 3 \sqrt{6 x^{3}}\)
    8. \(\sqrt[3]{4}(\sqrt[3]{16}-\sqrt[3]{6})\)
    9. \((4-3 \sqrt{3})(5+2 \sqrt{3})\)
    10. \(\frac{\sqrt[3]{128}}{\sqrt[3]{54}}\)
    11. \(\frac{\sqrt{245 x y^{-4}}}{\sqrt{45 x^{4} y^{3}}}\)
    12. \(\frac{1}{\sqrt[3]{5}}\)
    13. \(\frac{3}{2+\sqrt{3}}\)
    14. \(\sqrt{-4} \cdot \sqrt{-9}\)
    15. \(-4 i(-2-3 i)\)
    16. \(\frac{4+i}{3-2 i}\)
    17. \(i^{172}\)
    回答

    1。

    1. \(\frac{1}{4}\)
    2. \(-343\)

    3。 \(x^{\frac{7}{4}}\)

    5。 \(-x^{2} \sqrt{3 x}\)

    7。 \(36 x^{4} \sqrt{2}\)

    9。 \(2-7 \sqrt{3}\)

    11。 \(\frac{7 x^{5}}{3 y^{7}}\)

    13。 \(3(2-\sqrt{3})\)

    15。 \(-12+8i\)

    17。 \(-i\)

    练习\(\PageIndex{35}\)

    在以下练习中，求解。

    1. \(\sqrt{2 x+5}+8=6\)
    2. \(\sqrt{x+5}+1=x\)
    3. \(\sqrt[3]{2 x^{2}-6 x-23}=\sqrt[3]{x^{2}-3 x+5}\)
    回答

    2。 \(x=4\)

    练习\(\PageIndex{36}\)

    在以下练习中，

    1. 找到函数的域
    2. 绘制函数图
    3. 使用图表确定范围
    1. \(g(x)=\sqrt{x+2}\)
    回答

    1。

    1. 域:\([-2, \infty)\)

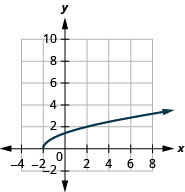
    2. 该图显示了 x y 坐标平面上的平方根函数图。 平面的 x 轴从负 2 延伸到 6。 y 轴从 0 到 8 延伸。 该函数的起点为（负 2, 0），并穿过两个点（负 1, 1）和（2, 2）。
      图 8.E.3
    3. 范围：\([0, \infty)\)