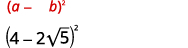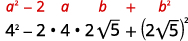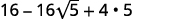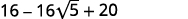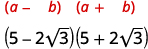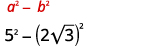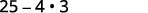8.5：加、减和乘激进表达式

Last updated
Save as PDF

Page ID: 204026

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

加减激进表达式
乘以激进表达式
使用多项式乘法将激进表达式相乘

在开始之前，请参加这个准备测验。

添加：$3x^{2}+9x−5−(x^{2}−2x+3)$。
如果您错过了此问题，请查看示例 5.5。
简化：$(2+a)(4−a)$。
如果您错过了此问题，请查看示例 5.28。
简化：$(9−5y)^{2}$。
如果您错过了此问题，请查看示例 5.31。

添加和减去激进表达式

添加具有相同索引和相同基数的激进表达式就像添加相似的术语一样。我们将激进分子的指数和激进分子称为激进分子，以提醒我们它们的作用与相似术语相同。

定义$\PageIndex{1}$: Like Radicals

类似 radicals 是具有相同索引和相同基数的激进表达式。

我们像激进项一样添加和减去，就像加减相似项一样。我们知道那$3x+8x$是$11x$。同样，我们$3 \sqrt{x}+8 \sqrt{x}$加上，结果是$11 \sqrt{x}$。

考虑在接下来的几个示例中添加带有变量的相似术语。当你有类似的自由基时，你只需将系数相加或减去即可。当激进分子不一样时，你就无法将这两个术语组合起来。

示例$\PageIndex{1}$

简化：

$2 \sqrt{2}-7 \sqrt{2}$
$5 \sqrt[3]{y}+4 \sqrt[3]{y}$
$7 \sqrt[4]{x}-2 \sqrt[4]{y}$

解决方案：

一个。

$2 \sqrt{2}-7 \sqrt{2}$

由于自由基是相似的，所以我们减去系数。

$-5 \sqrt{2}$

b。

$5 \sqrt[3]{y}+4 \sqrt[3]{y}$

由于自由基是相似的，所以我们添加系数。

$9 \sqrt[3]{y}$

c。

$7 \sqrt[4]{x}-2 \sqrt[4]{y}$

指数相同，但激进分子不同。他们不像激进分子。既然激进分子不一样，我们就无法减去他们。

练习$\PageIndex{1}$

简化：

$8 \sqrt{2}-9 \sqrt{2}$
$4 \sqrt[3]{x}+7 \sqrt[3]{x}$
$3 \sqrt[4]{x}-5 \sqrt[4]{y}$

回答

$-\sqrt{2}$
$11 \sqrt[3]{x}$
$3 \sqrt[4]{x}-5 \sqrt[4]{y}$

练习$\PageIndex{2}$

简化：

$5 \sqrt{3}-9 \sqrt{3}$
$5 \sqrt[3]{y}+3 \sqrt[3]{y}$
$5 \sqrt[4]{m}-2 \sqrt[3]{m}$

回答

$-4 \sqrt{3}$
$8 \sqrt[3]{y}$
$5 \sqrt[4]{m}-2 \sqrt[3]{m}$

要使激进分子相似，它们必须具有相同的指数和激进分数。当基数包含多个变量时，只要所有变量及其指数相同，则基数是相同的。

示例$\PageIndex{2}$

简化：

$2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}$
$\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}$

解决方案：

一个。

$2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}$

既然激进分子就像这样，我们就把他们结合起来。

$0 \sqrt{5 n}$

简化。

$0$

b。

$\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}$

既然激进分子就像这样，我们就把他们结合起来。

$2 \sqrt[4]{3 x y}$

练习$\PageIndex{3}$

简化：

$\sqrt{7 x}-7 \sqrt{7 x}+4 \sqrt{7 x}$
$4 \sqrt[4]{5 x y}+2 \sqrt[4]{5 x y}-7 \sqrt[4]{5 x y}$

回答

$-2 \sqrt{7 x}$
$-\sqrt[4]{5 x y}$

练习$\PageIndex{4}$

简化：

$4 \sqrt{3 y}-7 \sqrt{3 y}+2 \sqrt{3 y}$
$6 \sqrt[3]{7 m n}+\sqrt[3]{7 m n}-4 \sqrt[3]{7 m n}$

回答

$-\sqrt{3 y}$
$3 \sqrt[3]{7 m n}$

请记住，我们总是通过从基数中移除最大因子（即指数的幂次方）来简化激进值。一旦每个激进分子都被简化了，我们就可以决定它们是否像激进分子一样。

示例$\PageIndex{3}$

简化：

$\sqrt{20}+3 \sqrt{5}$
$\sqrt[3]{24}-\sqrt[3]{375}$
$\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}$

解决方案：

一个。

$\sqrt{20}+3 \sqrt{5}$

尽可能简化激进分子。

$\sqrt{4} \cdot \sqrt{5}+3 \sqrt{5}$

$2 \sqrt{5}+3 \sqrt{5}$

将类似的激进分子结合起来。

$5 \sqrt{5}$

b。

$\sqrt[3]{24}-\sqrt[3]{375}$

简化激进分子。

$\sqrt[3]{8} \cdot \sqrt[3]{3}-\sqrt[3]{125} \cdot \sqrt[3]{3}$

$2 \sqrt[3]{3}-5 \sqrt[3]{3}$

将类似的激进分子结合起来。

$-3 \sqrt[3]{3}$

c。

$\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}$

简化激进分子。

$\frac{1}{2} \sqrt[4]{16} \cdot \sqrt[4]{3}-\frac{2}{3} \sqrt[4]{81} \cdot \sqrt[4]{3}$

$\frac{1}{2} \cdot 2 \cdot \sqrt[4]{3}-\frac{2}{3} \cdot 3 \cdot \sqrt[4]{3}$

$\sqrt[4]{3}-2 \sqrt[4]{3}$

将类似的激进分子结合起来。

$-\sqrt[4]{3}$

练习$\PageIndex{5}$

简化：

$\sqrt{18}+6 \sqrt{2}$
$6 \sqrt[3]{16}-2 \sqrt[3]{250}$
$\frac{2}{3} \sqrt[3]{81}-\frac{1}{2} \sqrt[3]{24}$

回答

$9 \sqrt{2}$
$2 \sqrt[3]{2}$
$\sqrt[3]{3}$

练习$\PageIndex{6}$

简化：

$\sqrt{27}+4 \sqrt{3}$
$4 \sqrt[3]{5}-7 \sqrt[3]{40}$
$\frac{1}{2} \sqrt[3]{128}-\frac{5}{3} \sqrt[3]{54}$

回答

$7 \sqrt{3}$
$-10 \sqrt[3]{5}$
$-3 \sqrt[3]{2}$

在下一个示例中，我们将从基数中移除常数和可变因子。既然我们已经练习了取变量的偶数根和奇数根，现在我们通常的做法是假设所有变量都大于或等于零，这样就不需要绝对值了。在本章的其余部分中，我们将使用这个假设。

示例$\PageIndex{4}$

简化：

$9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}$
$\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}$

解决方案：

一个。

$9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}$

简化激进分子。

$9 \sqrt{25 m^{2}} \cdot \sqrt{2}-6 \sqrt{16 m^{2}} \cdot \sqrt{3}$

$9 \cdot 5 m \cdot \sqrt{2}-6 \cdot 4 m \cdot \sqrt{3}$

$45 m \sqrt{2}-24 m \sqrt{3}$

激进分子不一样，因此无法合并。

b。

$\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}$

简化激进分子。

$\sqrt[3]{27 n^{3}} \cdot \sqrt[3]{2 n^{2}}-\sqrt[3]{8 n^{3}} \cdot \sqrt[3]{2 n^{2}}$

$3 n \sqrt[3]{2 n^{2}}-2 n \sqrt[3]{2 n^{2}}$

将类似的激进分子结合起来。

$n \sqrt[3]{2 n^{2}}$

练习$\PageIndex{7}$

简化：

$\sqrt{32 m^{7}}-\sqrt{50 m^{7}}$
$\sqrt[3]{135 x^{7}}-\sqrt[3]{40 x^{7}}$

回答

$-m^{3} \sqrt{2 m}$
$x^{2} \sqrt[3]{5 x}$

练习$\PageIndex{8}$

简化：

$\sqrt{27 p^{3}}-\sqrt{48 p^{3}}$
$\sqrt[3]{256 y^{5}}-\sqrt[3]{32 n^{5}}$

回答

$-p \sqrt{3 p}$
$4 y \sqrt[3]{4 y^{2}}-2 n \sqrt[3]{4 n^{2}}$

乘以激进表达式

我们使用根的乘积属性通过移除完美平方因子来简化平方根。我们可以使用根的乘积属性 “反向” 来乘以平方根。请记住，我们假设所有变量都大于或等于零。

我们将重写 Roots 的产品属性，这样我们就可以一起看清两种情况。

定义$\PageIndex{2}$: Product Property of Roots

对于任何实数，$\sqrt[n]{a}$和$\sqrt[b]{n}$，对于任何整数$n≥2$

$\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b} \quad \text { and } \quad \sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}$

当我们将两个自由基相乘时，它们的索引必须相同。一旦我们乘以激进，我们就会寻找构成指数幂的因子，并尽可能简化激进。

将自由基与系数相乘很像将变量与系数相乘。要乘以$4x⋅3y$我们将系数乘在一起，然后再乘以变量。结果是$12xy$。在做这些例子时，请记住这一点。

示例$\PageIndex{5}$

简化：

$(6 \sqrt{2})(3 \sqrt{10})$
$(-5 \sqrt[3]{4})(-4 \sqrt[3]{6})$

解决方案：

一个。

$(6 \sqrt{2})(3 \sqrt{10})$

使用产品属性乘以。

$18\sqrt{20}$

简化激进。

$18 \sqrt{4} \cdot \sqrt{5}$

简化。

$18 \cdot 2 \cdot \sqrt{5}$

$36 \sqrt{5}$

b。

$(-5 \sqrt[3]{4})(-4 \sqrt[3]{6})$

使用产品属性乘以。

$20 \sqrt[3]{24}$

简化激进。

$20 \sqrt[3]{8} \cdot \sqrt[3]{3}$

简化。

$20 \cdot 2 \cdot \sqrt[3]{3}$

$40 \sqrt[3]{3}$

练习$\PageIndex{9}$

简化：

$(3 \sqrt{2})(2 \sqrt{30})$
$(2 \sqrt[3]{18})(-3 \sqrt[3]{6})$

回答

$12 \sqrt{15}$
$-18 \sqrt[3]{2}$

练习$\PageIndex{10}$

简化：

$(3 \sqrt{3})(3 \sqrt{6})$
$(-4 \sqrt[3]{9})(3 \sqrt[3]{6})$

回答

$27 \sqrt{2}$
$-36 \sqrt[3]{2}$

当激进分子中有变量时，我们遵循相同的程序。

示例$\PageIndex{6}$

简化：

$\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})$
$\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)$

解决方案：

一个。

$\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})$

乘以。

$40 \sqrt{18 p^{4}}$

简化激进。

$40 \sqrt{9 p^{4}} \cdot \sqrt{2}$

简化。

$40 \cdot 3 p^{2} \cdot \sqrt{3}$

$120 p^{2} \sqrt{3}$

b. 当激进分子涉及大量人员时，为了找到完美的力量，将它们考虑在内通常是有利的。

$\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)$

乘以。

$6 \sqrt[4]{4 \cdot 5 \cdot 4 \cdot 7 y^{5}}$

简化激进。

$6 \sqrt[4]{16 y^{4}} \cdot \sqrt[4]{35 y}$

简化。

$6 \cdot 2 y \sqrt[4]{35 y}$

乘以。

$12 y \sqrt[4]{35 y}$

练习$\PageIndex{11}$

简化：

$\left(6 \sqrt{6 x^{2}}\right)\left(8 \sqrt{30 x^{4}}\right)$
$\left(-4 \sqrt[4]{12 y^{3}}\right)\left(-\sqrt[4]{8 y^{3}}\right)$

回答

$36 x^{3} \sqrt{5}$
$8 y \sqrt[4]{3 y^{2}}$

练习$\PageIndex{12}$

简化：

$\left(2 \sqrt{6 y^{4}}\right)(12 \sqrt{30 y})$
$\left(-4 \sqrt[4]{9 a^{3}}\right)\left(3 \sqrt[4]{27 a^{2}}\right)$

回答

$144 y^{2} \sqrt{5 y}$
$-36 \sqrt[4]{3 a}$

使用多项式乘法将激进表达式相乘

在接下来的几个例子中，我们将使用 Di stributive Prop erty 将表达式与基数相乘。首先，我们将分发激进分子，然后尽可能简化激进分子。

示例$\PageIndex{7}$

简化：

$\sqrt{6}(\sqrt{2}+\sqrt{18})$
$\sqrt[3]{9}(5-\sqrt[3]{18})$

解决方案：

一个。

$\sqrt{6}(\sqrt{2}+\sqrt{18})$

乘以。

$\sqrt{12}+\sqrt{108}$

简化。

$\sqrt{4} \cdot \sqrt{3}+\sqrt{36} \cdot \sqrt{3}$

简化。

$2 \sqrt{3}+6 \sqrt{3}$

像激进分子一样结合。

$8\sqrt{3}$

b。

$\sqrt[3]{9}(5-\sqrt[3]{18})$

分发。

$5 \sqrt[3]{9}-\sqrt[3]{162}$

简化。

$5 \sqrt[3]{9}-\sqrt[3]{27} \cdot \sqrt[3]{6}$

简化。

$5 \sqrt[3]{9}-3 \sqrt[3]{6}$

练习$\PageIndex{13}$

简化：

$\sqrt{6}(1+3 \sqrt{6})$
$\sqrt[3]{4}(-2-\sqrt[3]{6})$

回答

$18+\sqrt{6}$
$-2 \sqrt[3]{4}-2 \sqrt[3]{3}$

练习$\PageIndex{14}$

简化：

$\sqrt{8}(2-5 \sqrt{8})$
$\sqrt[3]{3}(-\sqrt[3]{9}-\sqrt[3]{6})$

回答

$-40+4 \sqrt{2}$
$-3-\sqrt[3]{18}$

当我们处理多项式时，我们将二项式乘以二项式。请记住，在我们合并任何类似术语之前，这给了我们四种产品。为了确保获得所有四种产品，我们组织了工作——通常采用FOIL方法。

示例$\PageIndex{8}$

简化：

$(3-2 \sqrt{7})(4-2 \sqrt{7})$
$(\sqrt[3]{x}-2)(\sqrt[3]{x}+4)$

解决方案：

一个。

$(3-2 \sqrt{7})(4-2 \sqrt{7})$

乘以。

$12-6 \sqrt{7}-8 \sqrt{7}+4 \cdot 7$

简化。

$12-6 \sqrt{7}-8 \sqrt{7}+28$

将相似的术语组合在一起。

$40-14 \sqrt{7}$

b。

$(\sqrt[3]{x}-2)(\sqrt[3]{x}+4)$

乘以。

$\sqrt[3]{x^{2}}+4 \sqrt[3]{x}-2 \sqrt[3]{x}-8$

将相似的术语组合在一起。

$\sqrt[3]{x^{2}}+2 \sqrt[3]{x}-8$

练习$\PageIndex{15}$

简化：

$(6-3 \sqrt{7})(3+4 \sqrt{7})$
$(\sqrt[3]{x}-2)(\sqrt[3]{x}-3)$

回答

$-66+15 \sqrt{7}$
$\sqrt[3]{x^{2}}-5 \sqrt[3]{x}+6$

练习$\PageIndex{16}$

简化：

$(2-3 \sqrt{11})(4-\sqrt{11})$
$(\sqrt[3]{x}+1)(\sqrt[3]{x}+3)$

回答

$41-14 \sqrt{11}$
$\sqrt[3]{x^{2}}+4 \sqrt[3]{x}+3$

示例$\PageIndex{9}$

简化：$(3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})$

解决方案：

$(3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})$

乘以。

$3 \cdot 2+12 \sqrt{10}-\sqrt{10}-4 \cdot 5$

简化。

$6+12 \sqrt{10}-\sqrt{10}-20$

将相似的术语组合在一起。

$-14+11 \sqrt{10}$

练习$\PageIndex{17}$

简化：$(5 \sqrt{3}-\sqrt{7})(\sqrt{3}+2 \sqrt{7})$

回答: $1+9 \sqrt{21}$

练习$\PageIndex{18}$

简化：$(\sqrt{6}-3 \sqrt{8})(2 \sqrt{6}+\sqrt{8})$

回答: $-12-20 \sqrt{3}$

当我们之前乘以二项式时，识别一些特殊产品使我们的工作变得更容易。当我们乘以激进分子时也是如此。我们使用的特殊产品配方如下所示。

特殊产品

二项式方块

$\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}$

共轭物的乘积

$(a+b)(a-b)=a^{2}-b^{2}$

我们将在接下来的几个示例中使用特殊的产品配方。我们将从二项式方块图案的乘积开始。

示例$\PageIndex{10}$

简化：

$2+\sqrt{3})^{2}$
$(4-2 \sqrt{5})^{2}$

解决方案：

一个。

表 8.4.1
	$。$
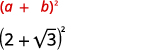使用二项式正方形图案的乘积进行乘法。	$。$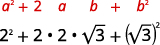
简化。	$。$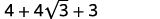
将相似的术语组合在一起。	$。$

b。

表 8.4.2
	$。$
多重，使用二项式正方形图案的乘积。	$。$
简化。	$。$
	$。$
将相似的术语组合在一起。	$。$

练习$\PageIndex{19}$

简化：

$(10+\sqrt{2})^{2}$
$(1+3 \sqrt{6})^{2}$

回答

$102+20 \sqrt{2}$
$55+6 \sqrt{6}$

练习$\PageIndex{20}$

简化：

$(6-\sqrt{5})^{2}$
$(9-2 \sqrt{10})^{2}$

回答

$41-12 \sqrt{5}$
$121-36 \sqrt{10}$

在下一个示例中，我们将使用共轭乘积模式。请注意，最终产品没有激进。

示例$\PageIndex{11}$

简化：$(5-2 \sqrt{3})(5+2 \sqrt{3})$

解决方案：

表 8.4.3
	$。$
使用共轭物乘积图案进行乘法。	$。$
简化。	$。$
	$。$

练习$\PageIndex{21}$

简化：$(3-2 \sqrt{5})(3+2 \sqrt{5})$

回答: $-11$

练习$\PageIndex{22}$

简化：$(4+5 \sqrt{7})(4-5 \sqrt{7})$

回答: $-159$

访问这些在线资源，获取更多指导和练习，包括加法、减法和乘法激进表达式。

乘法加减去自由基
乘以特殊产品：包含平方根的平方二项式
乘以共轭物

关键概念

根的产品特性
- 对于任何实数，$\sqrt[n]{a}$和$\sqrt[n]{b}$，对于任何整数$n≥2$$\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b}$和$\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}$
特殊产品

$\begin{array}{c c}{\text { Binomial Squares }}& {\text{Product of Conjugates}} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a+b)(a-b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}$

词汇表

像激进分子一样: 类似 radicals 是具有相同索引和相同基数的激进表达式。

定义\(\PageIndex{1}\): Like Radicals

示例\(\PageIndex{1}\)

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

示例\(\PageIndex{3}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

示例\(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

示例\(\PageIndex{5}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

示例\(\PageIndex{6}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

示例\(\PageIndex{7}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

示例\(\PageIndex{8}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

示例\(\PageIndex{9}\)

练习\(\PageIndex{17}\)

练习\(\PageIndex{18}\)

示例\(\PageIndex{10}\)

练习\(\PageIndex{19}\)

练习\(\PageIndex{20}\)

示例\(\PageIndex{11}\)

练习\(\PageIndex{21}\)

练习\(\PageIndex{22}\)