8.2: 使用根简化表达式
- Page ID
- 203993
在本节结束时,您将能够:
- 使用根简化表达式
- 估计和近似根源
- 使用根简化变量表达式
在开始之前,请参加这个准备测验。
- 简化:a.\((−9)^{2}\) b.\(-9^{2}\) c.\((−9)^{3}\)
如果你错过了这个问题,请查看示例 2.21。 - 四舍五入\(3.846\)到最接近的百分之一。
如果你错过了这个问题,请查看示例 1.34。 - 简化:a.\(x^{3} \cdot x^{3}\) b.\(y^{2} \cdot y^{2} \cdot y^{2}\) c.\(z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}\)
如果你错过了这个问题,请查看示例 5.12。
使用根简化表达式
在基金会中,我们简要介绍了平方根。 请记住,当一个实数\(n\)乘以自身时,我们将其写入\(n^{2}\)和读取 “\(n^{2}\)平方”。 这个数字被称为的平方\(n\),\(n\)被称为平方根。 例如,
\(13^{2}\)读为 “\(13\)平方”
\(169\)被称为 square of\(13\),因为\(13^{2}=169\)
\(13\)是的平方根\(169\)
正方形
如果\(n^{2}=m\),则\(m\)是的平方\(n\)。
平方根
如果\(n^{2}=m\),\(n\)则为的平方根\(m\)。
\((−13)^{2} = 169\)另请注意,的平方根\(−13\)也是如此\(169\)。 因此,\(13\)和\(−13\)都是的平方根\(169\)。
因此,每个正数都有两个平方根——一个正数和一个负数。 如果我们只想要一个正数的正平方根呢? 我们使用激进符号\(\sqrt{m}\),然后写上,表示的正平方根\(m\)。 正平方根也称为主平方根。
我们还使用激进符号来表示零的平方根。 因为\(0^{2}=0, \sqrt{0}=0\)。 请注意,零只有一个平方根。
\(\sqrt{m}\)读作 “的平方根”\(m\)。
如果\(n^{2}=m\),那么\(n=\sqrt{m}\),对于\(n\geq 0\)。
我们知道每个正数都有两个平方根,激进符号表示正数。 我们写\(\sqrt{169}=13\)。 如果我们想找到一个数字的负平方根,我们在激进符号前面放一个负数。 例如,\(-\sqrt{169}=-13\)。
简化:
- \(\sqrt{144}\)
- \(-\sqrt{289}\)
解决方案:
一个。
\(\sqrt{144}\)
从那以后\(12^{2}=144\)。
\(12\)
b。
\(-\sqrt{289}\)
Since\(17^{2}=289\) 和负数在激进符号的前面。
\(-17\)
简化:
- \(-\sqrt{64}\)
- \(\sqrt{225}\)
- 回答
-
- \(-8\)
- \(15\)
简化:
- \(\sqrt{100}\)
- \(-\sqrt{121}\)
- 回答
-
- \(10\)
- \(-11\)
我们可以简化\(-\sqrt{49}\)吗? 有数字的正方形\(-49\)吗?
\((\)___\( )^{2}=-49\)
任何正数的平方均为正数。 任何负数平方均为正数。 没有实数等于\(\sqrt{-49}\)。 负数的平方根不是实数。
简化:
- \(\sqrt{-196}\)
- \(-\sqrt{64}\)
解决方案:
一个。
\(\sqrt{-196}\)
没有实数的平方是\(-196\)。
\(\sqrt{-196}\)不是实数。
b。
\(-\sqrt{64}\)
负面因素在激进分子面前。
\(-8\)
简化:
- \(\sqrt{-169}\)
- \(-\sqrt{81}\)
- 回答
-
- 不是实数
- \(-9\)
简化:
- \(-\sqrt{49}\)
- \(\sqrt{-121}\)
- 回答
-
- \(-7\)
- 不是实数
到目前为止,我们只讨论了平方和平方根。 现在,让我们扩大工作范围,将更高的权力和更高的根源包括在内。
让我们先回顾一些词汇。
\(\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}\)
术语 “平方” 和 “立方体” 来自正方形面积和立方体体积的公式。
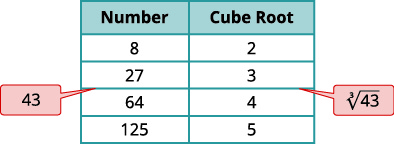
如果有一张表列出从\(−5\)到的整数的幂会很有帮助\(5\)。 参见图 8.1.2
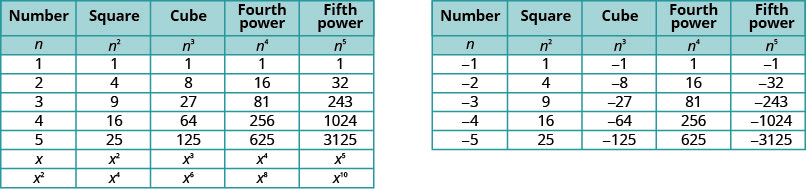
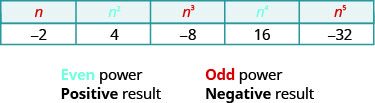
注意表格中的标志。 当然,所有正数的幂都是正数。 但是当我们有一个负数时,偶数幂是正数,奇数次方是负数。 我们将复制具有强度的行,\(−2\)以帮助您查看此内容。
现在,我们将把平方根定义扩展到更高的根。
如果\(b^{n}=a\),则\(b\)是的\(n^{th}\)根\(a\)。
的主要\(n^{th}\)根源\(a\)已写入\(\sqrt[n]{a}\)。
这\(n\)被称为激进分子的指数。
就像我们使用 “cubed” 这个词一样\(b^{3}\),我们使用 “cube root” 一词来表示\(\sqrt[3]{a}\)。
我们可以参考图 8.1.2 来帮助找到更高的根源。
\(\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}\)
我们可以有一个负数的偶数根吗? 我们知道负数的平方根不是实数。 任何偶数根也是如此。 负数的@@ 偶数根不是实数。 负数的@@ 奇数根是实数。
的属性\(\sqrt[n]{a}\)
什么时候\(n\)是偶数和
- \(a \geq 0\),则\(\sqrt[n]{a}\)是一个实数。
- \(a<0\),\(\sqrt[n]{a}\)则不是实数。
如果\(n\)是奇数,\(\sqrt[n]{a}\)则是所有值的实数\(a\)。
我们将在接下来的两个示例中应用这些属性。
简化:
- \(\sqrt[3]{64}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{32}\)
解决方案:
一个。
\(\sqrt[3]{64}\)
从那以后\(4^{3}=64\)。
\(4\)
b。
\(\sqrt[4]{81}\)
从那以后\((3)^{4}=81\)。
\(3\)
c。
\(\sqrt[5]{32}\)
从那以后\((2)^{5}=32\)。
\(2\)
简化:
- \(\sqrt[3]{27}\)
- \(\sqrt[4]{256}\)
- \(\sqrt[5]{243}\)
- 回答
-
- \(3\)
- \(4\)
- \(3\)
简化:
- \(\sqrt[3]{1000}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{243}\)
- 回答
-
- \(10\)
- \(2\)
- \(3\)
在这个例子中,要警惕负号以及偶数和奇数。
简化:
- \(\sqrt[3]{-125}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{-243}\)
解决方案:
一个。
\(\sqrt[3]{-125}\)
从那以后\((-5)^{3}=-125\)。
\(-5\)
b。
\(\sqrt[4]{16}\)
想想,\((?)^{4}=-16\)。 提高到第四次幂的实数都不是负数。
不是一个实数。
c。
\(\sqrt[5]{-243}\)
从那以后\((-3)^{5}=-243\)。
\(-3\)
简化:
- \(\sqrt[3]{-27}\)
- \(\sqrt[4]{-256}\)
- \(\sqrt[5]{-32}\)
- 回答
-
- \(-3\)
- 不是真的
- \(-2\)
简化:
- \(\sqrt[3]{-216}\)
- \(\sqrt[4]{-81}\)
- \(\sqrt[5]{-1024}\)
- 回答
-
- \(-6\)
- 不是真的
- \(-4\)
估计和近似根
当我们看到一个带有激进符号的数字时,我们通常不会考虑它的数值。 虽然我们可能知道\(\sqrt{4}=2\),但\(\sqrt{21}\)或的价值是多\(\sqrt[3]{50}\)少? 在某些情况下,快速估计是有意义的,而在另一些情况下,使用十进制近似值很方便。
为了获得平方根的数值估计值,我们寻找最接近基数的完美平方数。 为了得出估计值\(\sqrt{11}\),我们看到\(11\)的是介于完美平方数\(9\)和\(16\)更接近的之间\(9\)。 然后它的平方根将介于\(3\)和之间\(4\),但更接近\(3\)。
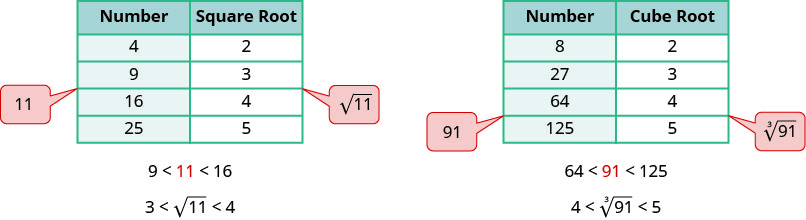
同样,为了估计\(\sqrt[3]{91}\),我们看到\(91\)的是介于完美立方数\(64\)和之间\(125\)。 然后,立方根将介于\(4\)和之间\(5\)。
估计两个连续整数之间的每个根:
- \(\sqrt{105}\)
- \(\sqrt[3]{43}\)
解决方案:
a. 想想最接近的完美平方数\(105\)。 用这些完美的正方形和它们的正方根做一张小桌子。
| \(\sqrt{105}\) | |
 |
|
| 位于两个连续的完美正方形\(105\)之间。 | \(100<\color{red}105 \color{black} <121\) |
| \(\sqrt{105}\)在它们的平方根之间。 | \(10< \color{red}\sqrt{105}< \color{black}11\) |
b. 同样,我们在两个完美的立方体数字\(43\)之间定位。
| \(\sqrt[3]{43}\) | |
 |
|
| 在两个连续的完美立方体\(43\)之间定位。 |  |
| \(\sqrt[3]{43}\)位于它们的立方根之间。 |  |
估计两个连续整数之间的每个根:
- \(\sqrt{38}\)
- \(\sqrt[3]{93}\)
- 回答
-
- \(6<\sqrt{38}<7\)
- \(4<\sqrt[3]{93}<5\)
估计两个连续整数之间的每个根:
- \(\sqrt{84}\)
- \(\sqrt[3]{152}\)
- 回答
-
- \(9<\sqrt{84}<10\)
- \(5<\sqrt[3]{152}<6\)
有一些数学方法可以近似平方根,但是现在大多数人使用计算器来计算平方根。 要找到平方根,你将使用计算器上的\(\sqrt{x}\)密钥。 要找到多维数据集根或任何具有更高索引的根,您将使用\(\sqrt[y]{x}\)密钥。
当你使用这些键时,你会得到一个近似值。 它是一个近似值,精确到计算器显示屏上显示的位数。 近似值的符号为\(≈\),读为 “近似”。
假设你的计算器有\(10\)数字显示屏。 你会明白的
\(\sqrt{5} \approx 2.236067978\)四舍五入到小数点后两位是\(\sqrt{5} \approx 2.24\)
\(\sqrt[4]{93} \approx 3.105422799\)四舍五入到小数点后两位是\(\sqrt[4]{93} \approx 3.11\)
我们怎么知道这些值是近似值而不是精确值? 看看当我们把它们对齐时会发生什么:
\(\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}\)
它们的平方接近\(5\)但不完全等于\(5\)。 第四次幂接近\(93\),但不等于\(93\)。
四舍五入到小数点后两位:
- \(\sqrt{17}\)
- \(\sqrt[3]{49}\)
- \(\sqrt[4]{51}\)
解决方案:
一个。
\(\sqrt{17}\)
使用计算器平方根键。
\(4.123105626 \dots\)
四舍五入到小数点后两位。
\(4.12\)
\(\sqrt{17} \approx 4.12\)
b。
\(\sqrt[3]{49}\)
使用计算器\(\sqrt[y]{x}\)密钥。
\(3.659305710 \ldots\)
四舍五入到小数点后两位。
\(3.66\)
\(\sqrt[3]{49} \approx 3.66\)
c。
\(\sqrt[4]{51}\)
使用计算器\(\sqrt[y]{x}\)密钥。
\(2.6723451177 \ldots\)
四舍五入到小数点后两位。
\(2.67\)
\(\sqrt[4]{51} \approx 2.67\)
四舍五入到小数点后两位:
- \(\sqrt{11}\)
- \(\sqrt[3]{71}\)
- \(\sqrt[4]{127}\)
- 回答
-
- \(\approx 3.32\)
- \(\approx 4.14\)
- \(\approx 3.36\)
四舍五入到小数点后两位:
- \(\sqrt{13}\)
- \(\sqrt[3]{84}\)
- \(\sqrt[4]{98}\)
- 回答
-
- \(\approx 3.61\)
- \(\approx 4.38\)
- \(\approx 3.15\)
使用根简化变量表达式
数字的奇数根可以是正数也可以是负数。 例如,
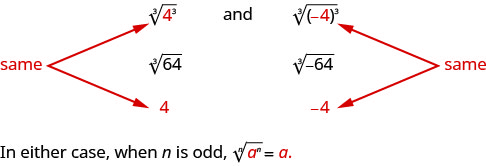
但是一个均匀的根呢? 我们想要主根,所以\(\sqrt[4]{625}=5\)。
但是请注意,
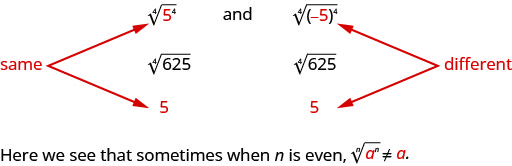
我们怎样才能确定\(−5\)提升到第四次幂的第四个根是\(5\)? 我们可以使用绝对值。 \(|−5|=5\)。 所以我们这样说什么时候\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)。 这保证了主根是正数。
对于任何整数\(n\geq 2\),
当索引\(n\)为奇数时\(\sqrt[n]{a^{n}}=a\)
当索引\(n\)为偶数时\(\sqrt[n]{a^{n}}=|a|\)
当我们取一个表达式的偶数根时,我们必须使用绝对值符号,其中一个变量是激进的。
简化:
- \(\sqrt{x^{2}}\)
- \(\sqrt[3]{n^{3}}\)
- \(\sqrt[4]{p^{4}}\)
- \(\sqrt[5]{y^{5}}\)
解决方案:
a. 我们使用绝对值来确保得到正根。
\(\sqrt{x^{2}}\)
由于索引\(n\)是偶数,\(\sqrt[n]{a^{n}}=|a|\).
b. 这是一个奇数索引根,因此不需要绝对值符号。
\(\sqrt[3]{m^{3}}\)
由于索引\(n\)是奇数,\(\sqrt[n]{a^{n}}=a\).
\(m\)
c。
\(\sqrt[4]{p^{4}}\)
由于索引\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)。
\(|p|\)
d。
\(\sqrt[5]{y^{5}}\)
由于索引\(n\)很奇怪,\(\sqrt[n]{a^{n}}=a\).
\(y\)
简化:
- \(\sqrt{b^{2}}\)
- \(\sqrt[3]{w^{3}}\)
- \(\sqrt[4]{m^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- 回答
-
- \(|b|\)
- \(w\)
- \(|m|\)
- \(q\)
简化:
- \(\sqrt{y^{2}}\)
- \(\sqrt[3]{p^{3}}\)
- \(\sqrt[4]{z^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- 回答
-
- \(|y|\)
- \(p\)
- \(|z|\)
- \(q\)
那么较高变量幂的平方根呢? 指数的力量属性是这样说\(\left(a^{m}\right)^{n}=a^{m \cdot n}\)的。 因此,如果我们进行平方\(a^{m}\),则指数将变成\(2m\)。
\(\left(a^{m}\right)^{2}=a^{2 m}\)
现在看平方根。
\(\sqrt{a^{2 m}}\)
从那以后\(\left(a^{m}\right)^{2}=a^{2 m}\)。
\(\sqrt{\left(a^{m}\right)^{2}}\)
因为\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)。
\(\left|a^{m}\right|\)
所以\(\sqrt{a^{2 m}}=\left|a^{m}\right|\)。
我们在下一个示例中应用了这个概念。
简化:
- \(\sqrt{x^{6}}\)
- \(\sqrt{y^{16}}\)
解决方案:
一个。
\(\sqrt{x^{6}}\)
从那以后\(\left(x^{3}\right)^{2}=x^{6}\)。
\(\sqrt{\left(x^{3}\right)^{2}}\)
由于索引\(n\)是偶数\(\sqrt{a^{n}}=|a|\)。
\(\left|x^{3}\right|\)
b。
\(\sqrt{y^{16}}\)
从那以后\(\left(y^{8}\right)^{2}=y^{16}\)。
\(\sqrt{\left(y^{8}\right)^{2}}\)
由于索引\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)。
\(y^{8}\)
在这种情况下,不需要绝对值符号,因为\(y^{8}\)它是正数。
简化:
- \(\sqrt{y^{18}}\)
- \(\sqrt{z^{12}}\)
- 回答
-
- \(|y^{9}|\)
- \(z^{6}\)
简化:
- \(\sqrt{m^{4}}\)
- \(\sqrt{b^{10}}\)
- 回答
-
- \(m^{2}\)
- \(|b^{5}|\)
下一个例子对更高的根使用相同的概念。
简化:
- \(\sqrt[3]{y^{18}}\)
- \(\sqrt[4]{z^{8}}\)
解决方案:
一个。
\(\sqrt[3]{y^{18}}\)
从那以后\(\left(y^{6}\right)^{3}=y^{18}\)。
\(\sqrt[3]{\left(y^{6}\right)^{3}}\)
因为\(n\)很奇怪,\(\sqrt[n]{a^{n}}=a\).
\(y^{6}\)
b。
\(\sqrt[4]{z^{8}}\)
从那以后\(\left(z^{2}\right)^{4}=z^{8}\)。
\(\sqrt[4]{\left(z^{2}\right)^{4}}\)
由于\(z^{2}\)是正数,因此我们不需要绝对值符号。
\(z^{2}\)
简化:
- \(\sqrt[4]{u^{12}}\)
- \(\sqrt[3]{v^{15}}\)
- 回答
-
- \(|u^{3}|\)
- \(v^{5}\)
简化:
- \(\sqrt[5]{c^{20}}\)
- \(\sqrt[6]{d^{24}}\)
- 回答
-
- \(c^{4}\)
- \(d^{4}\)
在下一个示例中,我们现在在变量前面有一个系数。 这个概念的\(\sqrt{a^{2 m}}=\left|a^{m}\right|\)运作方式大致相同。
\(\sqrt{16 r^{22}}=4\left|r^{11}\right|\)因为\(\left(4 r^{11}\right)^{2}=16 r^{22}\)。
但是请注意\(\sqrt{25 u^{8}}=5 u^{4}\),不需要绝对值符号,因为总是\(u^{4}\)正数。
简化:
- \(\sqrt{16 n^{2}}\)
- \(-\sqrt{81 c^{2}}\)
解决方案:
一个。
\(\sqrt{16 n^{2}}\)
从那以后\((4 n)^{2}=16 n^{2}\)。
\(\sqrt{(4 n)^{2}}\)
由于索引\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)。
\(4|n|\)
b。
\(-\sqrt{81 c^{2}}\)
从那以后\((9 c)^{2}=81 c^{2}\)。
\(-\sqrt{(9 c)^{2}}\)
由于索引\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)。
\(-9|c|\)
简化:
- \(\sqrt{64 x^{2}}\)
- \(-\sqrt{100 p^{2}}\)
- 回答
-
- \(8|x|\)
- \(-10|p|\)
简化:
- \(\sqrt{169 y^{2}}\)
- \(-\sqrt{121 y^{2}}\)
- 回答
-
- \(13|y|\)
- \(-11|y|\)
这个例子只是把这个想法推得更远,因为它的根源在于更高的指数。
简化:
- \(\sqrt[3]{64 p^{6}}\)
- \(\sqrt[4]{16 q^{12}}\)
解决方案:
一个。
\(\sqrt[3]{64 p^{6}}\)
重写\(64p^{6}\)为\(\left(4 p^{2}\right)^{3}\)。
\(\sqrt[3]{\left(4 p^{2}\right)^{3}}\)
取立方体根。
\(4p^{2}\)
b。
\(\sqrt[4]{16 q^{12}}\)
将激进分子重写为第四种力量。
\(\sqrt[4]{\left(2 q^{3}\right)^{4}}\)
取第四根根。
\(2|q^{3}|\)
简化:
- \(\sqrt[3]{27 x^{27}}\)
- \(\sqrt[4]{81 q^{28}}\)
- 回答
-
- \(3x^{9}\)
- \(3|q^{7}|\)
简化:
- \(\sqrt[3]{125 q^{9}}\)
- \(\sqrt[5]{243 q^{25}}\)
- 回答
-
- \(5p^{3}\)
- \(3q^{5}\)
接下来的例子有两个变量。
简化:
- \(\sqrt{36 x^{2} y^{2}}\)
- \(\sqrt{121 a^{6} b^{8}}\)
- \(\sqrt[3]{64 p^{63} q^{9}}\)
解决方案:
一个。
\(\sqrt{36 x^{2} y^{2}}\)
由于\((6 x y)^{2}=36 x^{2} y^{2}\)
\(\sqrt{(6 x y)^{2}}\)
取平方根。
\(6|xy|\)
b。
\(\sqrt{121 a^{6} b^{8}}\)
由于\(\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}\)
\(\sqrt{\left(11 a^{3} b^{4}\right)^{2}}\)
取平方根。
\(11\left|a^{3}\right| b^{4}\)
c。
\(\sqrt[3]{64 p^{63} q^{9}}\)
由于\(\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}\)
\(\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}\)
取立方体根。
\(4p^{21}q^{3}\)
简化:
- \(\sqrt{100 a^{2} b^{2}}\)
- \(\sqrt{144 p^{12} q^{20}}\)
- \(\sqrt[3]{8 x^{30} y^{12}}\)
- 回答
-
- \(10|ab|\)
- \(12p^{6}q^{10}\)
- \(2x^{10}y^{4}\)
简化:
- \(\sqrt{225 m^{2} n^{2}}\)
- \(\sqrt{169 x^{10} y^{14}}\)
- \(\sqrt[3]{27 w^{36} z^{15}}\)
- 回答
-
- \(15|mn|\)
- \(13\left|x^{5} y^{7}\right|\)
- \(3w^{12}z^{5}\)
访问此在线资源以获取更多指导和练习,使用根简化表达式。
- 使用绝对值简化变量带根的指数
关键概念
- 平方根表示法
- \(\sqrt{m}\)被读为 “的平方根\(m\)”
- 如果\(n^{2}=m\),那么\(n=\sqrt{m}\),对于\(n≥0\)。
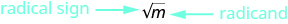
图 8.1.1 - 的平方根是一个正数\(m\)\(\sqrt{m}\),其平方为\(m\)。
- n 个数字的根
- 如果\(b^{n}=a\),则\(b\)是的\(n^{th}\)根\(a\)。
- 的主要\(n^{th}\)根源\(a\)已写入\(\sqrt[n]{a}\)。
- \(n\)被称为激进分子的指数。
- 的属性\(\sqrt[n]{a}\)
- 什么时候\(n\)是偶数和
- \(a≥0\),那么\(\sqrt[n]{a}\)是一个实数
- \(a<0\),那么\(\sqrt[n]{a}\)不是一个实数
- 如果\(n\)是奇数,\(\sqrt[n]{a}\)则是所有值的实数\(a\)。
- 什么时候\(n\)是偶数和
- 简化奇数和偶数根
- 对于任何整数\(n≥2\),
- 什么时候\(n\)是奇数\(\sqrt[n]{a^{n}}=a\)
- 什么时候\(n\)是偶数\(\sqrt[n]{a^{n}}=|a|\)
- 当我们取一个表达式的偶数根时,我们必须使用绝对值符号,其中一个变量是激进的。
- 对于任何整数\(n≥2\),
词汇表
- 数字的平方
- 如果\(n^{2}=m\),则\(m\)是的平方\(n\)。
- 数字的平方根
- 如果\(n^{2}=m\),\(n\)则为的平方根\(m\)。


