2.7E：练习

Last updated
Save as PDF

Page ID: 204322

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

练习成就完美

用 “and” 求解复合不等式

在以下练习中，求解每个不等式，绘出解图，然后用区间表示法写出解。

1。 $x<3$和$x\geq 1$

2。 $x\leq 4$和$x>−2$

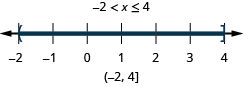
回答: $解为负 2 小于 x，即小于或等于 4。它的图形在 1negative 2 处有一个开圆，在 4 处有一个封闭的圆，开放圆和封闭的圆之间有阴影。它的间隔符号在圆括号和括号内为负 2 到 4。$

3。 $x\geq −4$和$x\leq −1$

4。 $x>−6$和$x<−3$

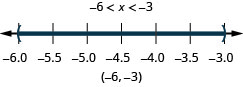
回答: $解为负 6 小于 x，后者小于负 3。它的图形在负6处有一个空圆，在负3处有一个空圆，空心圆之间有阴影。其间隔表示法在括号内为负 6 到负 3。$

5。 $5x−2<8$和$6x+9\geq 3$

6。 $4x−1<7$和$2x+8\geq 4$

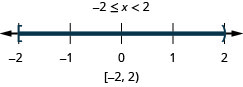
回答: $解为负 2 小于或等于 x，后者小于 2。它的图形在负2处有一个封闭的圆，在2处有一个空圆，封闭圆和空心圆之间有阴影。在方括号和括号中，它的间隔表示法是负数 2 到 2。$

7。 $4x+6\leq 2$和$2x+1\geq −5$

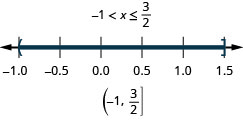
8。 $4x−2\leq 4$和$7x−1>−8$

回答: $解为负 1 小于 x，即小于或等于三半。它的图形在负1处有一个开圆，在三半处有一个封闭的圆，开放圆和封闭的圆之间有阴影。它的间隔表示法在圆括号和括号内为负 1 到三半。$

9。 $2x−11<5$和$3x−8>−5$

10。 $7x−8<6$和$5x+7>−3$

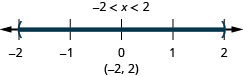
回答: $解为负 2 小于 x，后者小于 2。它的图形在负2处有一个空圆，在2处有一个空圆，空心圆之间有阴影。其间隔表示法在括号内为负 2 到 2。$

11。 $4(2x−1)\leq 12$和$2(x+1)<4$

12。 $5(3x−2)\leq 5$和$3(x+3)<3$

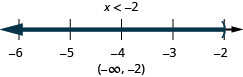
回答: $解是 x 小于负 2。它的图形在负 2 处有一个空心圆圈，左边有阴影。其间隔表示法在括号内为负无穷大到负 2。$

13。 $3(2x−3)>3$和$4(x+5)\geq 4$

14。 $−3(x+4)<0$和$−1(3x−1)\leq 7$

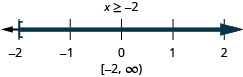
回答: $解是 x 大于或等于负 2。它的图形在负 2 处有一个封闭的圆圈，右边有阴影。它的间隔表示法在方括号和括号内为负 2 到无穷大。$

15。 $\frac{1}{2}(3x−4)\leq 1$和$\frac{1}{3}(x+6)\leq 4$

16。 $\frac{3}{4}(x−8)\leq 3$和$\frac{1}{5}(x−5)\leq 3$

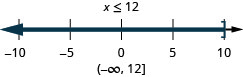
回答: $解是 x 小于或等于 12。它的图形在 12 点处有一个封闭的圆圈，左边有阴影。它的间隔表示法在圆括号和括号内为负无穷大到 12。$

17。 $5x−2\leq 3x+4$和$3x−4\geq 2x+1$

18。 $\frac{3}{4}x−5\geq −2$和$−3(x+1)\geq 6$

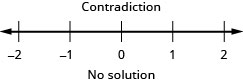
回答: $解决方案是矛盾的。所以，没有解决办法。因此，没有图表、数字线或间隔符号。$

19。 $\frac{2}{3}x−6\geq −4$和$−4(x+2)\geq 0$

20。 $\frac{1}{2}(x−6)+2<−5$和$4−\frac{2}{3}x<6$

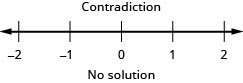
回答: $解决方案是矛盾的。所以，没有解决办法。因此，没有图表、数字线或间隔符号。$

21。 $−5\leq 4x−1<7$

22。 $−3<2x−5\leq 1$

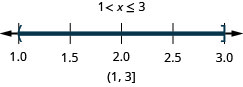
回答: $解为 1 小于 x，即小于或等于 3。它的图形在 1 处有一个开的圆，在 3 处有一个封闭的圆，在开放圆和封闭的圆之间有阴影。在圆括号和括号中，其间隔符号为 1 到 3。$

23。 $5<4x+1<9$

24。 $−1<3x+2<8$

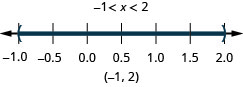
回答: $解为负 1 小于 x，后者小于 2。它的图形在负 1 处有一个空圆，在 2 处有一个空圆，中间有阴影。其间隔表示法在括号内为负 1 到 2。$

25。 $−8<5x+2\leq −3$

26。 $−6\leq 4x−2<−2$

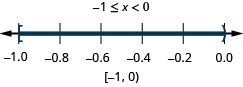
回答: $解为负 1 小于或等于 x，后者小于或 0。它的图形在负 1 处有一个封闭的圆，在 0 处有一个开的圆，在封闭圆和空心圆之间有阴影。在方括号和括号中，它的间隔表示法是负数 1 到 0。$

用 “或” 求解复合不等式

在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

27。 $x\leq −2$或$x>3$

28。 $x\leq −4$或$x>−3$

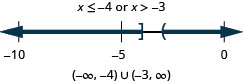
回答: $解是 x 小于或等于负 4 或 x 大于负 3。数字线上的解图在负4处有一个闭合的圆圈，左边是阴影，在负3处有一个空的圆圈，右边是阴影。间隔表示法是圆括号和方括号内的负无穷大与负 4 的并集，括号中的负 3 和无穷大的并集。$

29。 $x<2$或$x\geq 5$

30。 $x<0$或$x\geq 4$

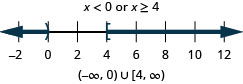
回答: $解是 x 小于 0 或 x 大于或等于 2。数字线上的解图在 0 处有一个空心圆圈，左边是阴影，4 处有一个封闭的圆圈，右边是阴影。间隔表示法是圆括号内负无穷大到 0 的并集，括号和圆括号内的 4 到无穷大的并集。$

31。 $2+3x\leq 4$或$5−2x\leq −1$

32。 $4−3x\leq −2$或$2x−1\leq −5$

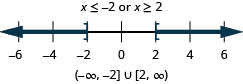
回答: $解是 x 小于或等于负 2 或 x 大于或等于 2。数字线上的解图在负 2 处有一个封闭的圆圈，左边是阴影，2 处有一个封闭的圆圈，右边是阴影。间隔表示法是指在圆括号和方括号内负无穷大到负 2 的并集，以及方括号和括号内的 2 到无穷大的并集。$

33。 $2(3x−1)<4$或$3x−5>1$

34。 $3(2x−3)<−5$或
$4x−1>3$

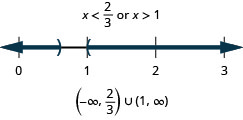
回答: $解是 x 小于三分之二或 x 大于 1。数字线上的解图在三分之二处有一个空心圆圈，左边是阴影，在1处有一个空的圆圈，右边是阴影。区间表示法是圆括号内负无穷大与三分之二的并集，圆括号内为 1 和无穷大。$

35。 $\frac{3}{4}x−2>4$或$4(2−x)>0$

36。 $\frac{2}{3}x−3>5$或$3(5−x)>6$

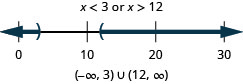
回答: $解是 x 小于 3 或 x 大于 12。数字线上的解图在 3 处有一个空心圆圈，左边是阴影，12 处有一个空的圆圈，右边是阴影。区间表示法是圆括号内负无穷大与 3 的并集，括号内为 12 和无穷大。$

37。 $3x−2>4$或$5x−3\leq 7$

38。 $2(x+3)\geq 0$或$3(x+4)\leq 6$

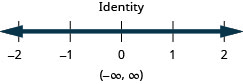
回答: $解决方案是身份。它在数字线上的解为所有值的阴影。区间表示法中的解是圆括号内的负无穷大到无穷大。$

39。 $\frac{1}{2}x−3\leq 4$或$\frac{1}{3}(x−6)\geq −2$

40。 $\frac{3}{4}x+2\leq −1$或$\frac{1}{2}(x+8)\geq −3$

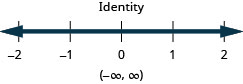
回答: $解决方案是身份。它在数字线上的解为所有值的阴影。区间表示法中的解是圆括号内的负无穷大到无穷大。$

混合练习

在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

41。 $3x+7\leq 1$和$2x+3\geq −5$

42。 $6(2x−1)>6$和$5(x+2)\geq 0$

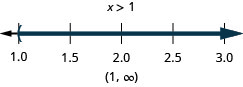
回答: $解是 x 小于 1。它的图形在负1处有一个开放的圆圈，右边有阴影。它的间隔表示法在圆括号内为 1 到无穷大。$

43。 $4−7x\geq −3$或$5(x−3)+8>3$

44。 $\frac{1}{2}x−5\leq 3$或$\frac{1}{4}(x−8)\geq −3$

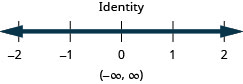
回答: $解决方案是身份。它在数字线上的解为所有值的阴影。区间表示法中的解是圆括号内的负无穷大到无穷大。$

45。 $−5\leq 2x−1<7$

46。 $\frac{1}{5}(x−5)+6<4$和$3−\frac{2}{3}x<5$

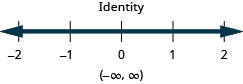
回答: $不平等是矛盾的。所以，没有解决办法。因此，数字线或间隔符号上没有图表。$

47。 $4x−2>6$或$3x−1\leq −2$

48。 $6x−3\leq 1$和$5x−1>−6$

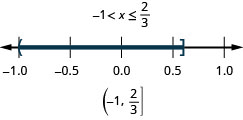
回答: $解为负 1 小于 x，即小于或等于三分之二。它的图形在负1处有一个开圆，在三分之二处有一个封闭的圆，在开圆和闭合的圆之间有阴影。在圆括号和括号中，它的间隔表示法为负数 1 到三分之二。$

49。 $−2(3x−4)\leq 2$和$−4(x−1)<2$

50。 $−5\leq 3x−2\leq 4$

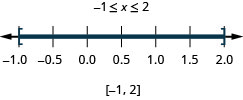
回答: $解为负 1 小于或等于 x，后者小于 2。它的图形在负1处有一个封闭的圆，在2处有一个封闭的圆，并且在封闭的圆之间有阴影。其间隔表示法在方括号内为负 1 到 4。$

使用复合不等式求解应用程序

在以下练习中，求解。

51。佩内洛普正在和姐姐 June 玩数字游戏。佩内洛普正在考虑一个数字，想让六月猜出来。她的号码超过三倍的五倍介于 2 和 32 之间。写一个复合不等式，显示佩内洛普可能想到的数字范围。

52。格雷戈里在想一个数字，他想让他的妹妹劳伦猜出这个数字。他的第一个线索是，六个小于他数字的两倍在四到四十二之间。写一个复合不等式，显示格雷戈里可能想到的数字范围。

回答: $5\leq n\leq 24$

53。安德鲁正在他的后院制作一只矩形的狗跑道。狗跑的长度为 18 英尺。狗跑的周长必须至少为 42 英尺且不超过 72 英尺。使用复合不等式来找出狗跑宽度的值范围。

54。 Elouise 正在她的后院建造一个矩形花园。花园的长度为 12 英尺。花园的周长必须至少为 36 英尺且不超过 48 英尺。使用复合不等式来查找花园宽度的值范围。

回答: $6\leq w\leq 12$

日常数学

55。血压一个人的血压是用两个数字来衡量的。收缩压测量心跳时动脉血液的压力。舒张压测量心脏休息时的压力。

ⓐ 让 x 成为你的收缩压。研究然后写出复合不等式，告诉你这个年龄的人的正常收缩压应该是多少。

ⓑ 让 y 成为你的舒张压。研究然后写出复合不等式，告诉你这个年龄的人的正常舒张压应该是多少。

56。体重指数（BMI）是根据您的身高和体重来衡量体内脂肪的指标。

ⓐ 让 x 成为你的 BMI。研究然后写出复合不等式来显示体重指数范围，让你被视为正常体重。

ⓑ 研究一个 BMI 计算器并确定你的 BMI。这是解决（a）部分不平等的解决方案吗？

回答: ⓐ 答案各不相同 ⓑ 答案各不相同

写作练习

57。用你自己的话说，解释平等的属性和不等式的属性之间的区别。

58。解释解决复合不等式的步骤$2−7x\geq −5$或$4(x−3)+7>3$.

回答: 答案会有所不同。

自检

ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。

$此表有四列和四行。第一行是标题，它会将每列标记为 “我可以...”、“自信”、“有帮助” 和 “不我不明白！” 在第 2 行中，我能用 “and” 求解复合不等式。在第 3 行中，“我能” 是用 “或” 求解复合不等式。在第 4 行中，“我能” 是求解具有复合不等式的应用程序。$

ⓑ 这份清单告诉你你对本部分的掌握情况了什么？你会采取哪些措施来改进？