2.8: 求解绝对值不等式
- Page ID
- 204224
在本节结束时,您将能够:
- 求解绝对值方程
- 用 “小于” 求解绝对值不等式
- 用 “大于” 求解绝对值不等式
- 用绝对值求解应用程序
在开始之前,请参加这个准备测验。
求解绝对值方程
在我们准备求解绝对值方程时,我们会回顾我们对绝对值的定义。
数字的绝对值是它在数字线上与零的距离。
数字 n 的绝对值写成所有数字\(|n|\)的\(|n|\geq 0\) and。
绝对值始终大于或等于零。
我们了解到,在数字线上,数字及其对数与零的距离是相同的。 由于它们与零的距离相同,因此它们的绝对值相同。 例如:
- \(−5\)距离 0 有 5 个单位的距离,所以\(|−5|=5\)。
- \(5\)距离 0 有 5 个单位的距离,所以\(|5|=5\)。
该图\(\PageIndex{1}\)说明了这个想法。
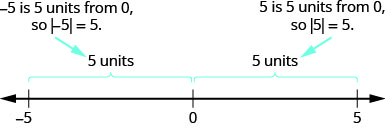
对于方程 |x|=5, |x|=5,我们正在寻找所有能使其成为真实陈述的数字。 我们正在寻找与零的距离为 5 的数字。 我们刚刚看到 5 和 −5−5 在数字行上都是从零开始的五个单位。 它们是方程的解。
\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)
通过写作,可以将解决方案简化为单个语句\(x=\pm 5\)。 读作 “x 等于正或负 5”。
我们可以将其概括为绝对值方程的以下属性。
对于任何代数表达式 u 和任何正实数 a
\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]
请记住,绝对值不能是负数。
解决:
- \(|x|=8\)
- \(|y|=−6\)
- \(|z|=0\)
- 解决方案 a
-
\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)
- 解决方案 b
-
\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\)
由于绝对值始终为正,因此该方程没有解。 - 解决方案 c
-
\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\)
两个方程都告诉我们 z=0z=0 所以只有一个解。
解决:
- \(|x|=2\)
- \(|y|=−4\)
- \(|z|=0\)
- 回答 a
-
\(\pm 2\)
- 答案 b
-
没有解决办法
- 答案 c
-
0
解决:
- \(|x|=11\)
- \(|y|=−5\)
- \(|z|=0\)
- 回答 a
-
\(\pm 11\)
- 答案 b
-
没有解决办法
- 答案 c
-
0
为了求解绝对值方程,我们首先使用与求解线性方程相同的程序隔离绝对值表达式。 隔离绝对值表达式后,我们将其重写为两个等效方程。
如何求解绝对值方程
解决\(|5x−4|−3=8\)。
- 解决方案
-




解决:\(|3x−5|−1=6\)。
- 回答
-
\(x=4, \space x=−\frac{2}{3}\)
解决:\(|4x−3|−5=2\)。
- 回答
-
\(x=−1,\space x=\frac{5}{2}\)
这里总结了求解绝对值方程的步骤。
- 隔离绝对值表达式。
- 写出等效方程式。
- 求解每个方程。
- 检查每种解决方案。
解决\(2|x−7|+5=9\).
- 解决方案
-
\(2|x−7|+5=9\) 隔离绝对值表达式。 \(2|x−7|=4\) \(|x−7|=2\) 写出等效方程式。 \(x−7=−2\)或\(x−7=2\) 求解每个方程。 \(x=5\)或\(x=9\) 查看:
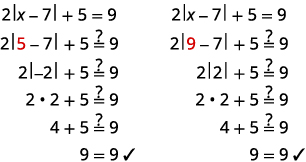
解决:\(3|x−4|−4=8\)。
- 回答
-
\(x=8,\space x=0\)
解决:\(2|x−5|+3=9\)。
- 回答
-
\(x=8,\space x=2\)
记住,绝对值总是正数!
解决:\(|\frac{2}{3}x−4|+11=3\)。
- 解决方案
-
\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)
解决:\(|\frac{3}{4}x−5|+9=4\)。
- 回答
-
没有解决办法
解决:\(|\frac{5}{6}x+3|+8=6\)。
- 回答
-
没有解决办法
我们的一些绝对值方程可能采用其\(|u|=|v|\)中 u 和 v 是代数表达式的形式。 例如,\(|x−3|=|2x+1|\)。
我们将如何解决这些问题? 如果两个代数表达式的绝对值相等,则它们要么彼此相等,要么彼此为负数。 绝对值方程的属性表示,对于任何代数表达式 u 和正实数,a、if\(|u|=a\)、then\(u=−a\) 或\(u=a\)。
这告诉我们了
\ (\ begin {array}
{lll} {\ text {if}} & {|u|=|v|}
& {}\\ {\ text {then}} & {|u|=v} & {|u|=−v}
\\ {\ text {and so}} & {u=v\ text {or} u = −v} & {\ text {or}} & {u=−v\ text {or} u = − (−v)}
\\\ end {array}\)
这使我们得出具有两个绝对值的方程的以下属性。
对于任何代数表达式 u 和 v,
\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]
当我们取与数量相反的值时,我们必须谨慎对待符号,并在需要时添加圆括号。
解决:\(|5x−1|=|2x+3|\)。
- 解决方案
-
\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)
解决:\(|7x−3|=|3x+7|\)。
- 回答
-
\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)
解决:\(|6x−5|=|3x+4|\)。
- 回答
-
\(x=3, x=19\)
用 “小于” 求解绝对值不等式
现在让我们来看看当我们存在绝对值不等式时会发生什么。 我们所学到的关于解决不平等的一切仍然有效,但我们必须考虑绝对价值如何影响我们的工作。 再说一遍,我们将看看我们对绝对值的定义。 数字的绝对值是它在数字线上与零的距离。 对于方程\(|x|=5\),我们看到数字线上\(−5\)的 5 和 5 都是 0 的五个单位。 它们是方程的解。
\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]
那不平等\(|x|\leq 5\)呢? 距离小于或等于 5 的数字在哪里? 我们知道\(−5\)和 5 都是从零开始的五个单位。 \(−5\)和 5 之间的所有数字从零开始小于五个单位(图\(\PageIndex{2}\))。
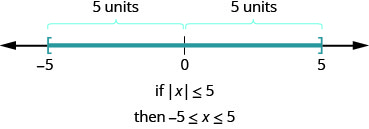
用更一般的方式,我们可以看出 if\(|u|\leq a\),那么\(−a\leq u\leq a\)(图\(\PageIndex{3}\))。
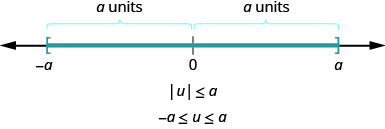
此处总结了此结果。
对于任何代数表达式 u 和任何正实数 a
\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]
求解不等式后,检查一些点以查看解是否有意义通常会很有帮助。 解的图形将数字线分为三个部分。 在每个部分中选择一个值,然后将其替换为原始不等式,以查看它是否使不等式成立。 虽然这不是一项完整的检查,但它通常有助于验证解决方案。
解决\(|x|<7\)。 绘制解图并用区间表示法写出解。
- 解决方案
-
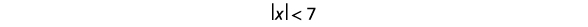
写下等效的不等式。 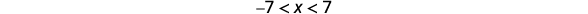
绘制解决方案的图表。 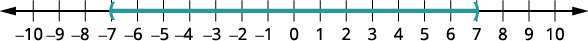
使用间隔表示法写出解。 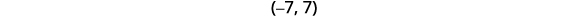
查看:
要进行验证,请检查显示解决方案的数字行的每个部分中的一个值。 选择诸如 −8、−8、1 和 9 之类的数字。
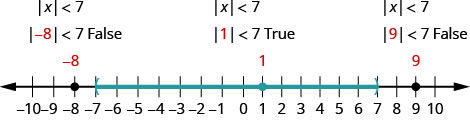
绘制解图并用区间表示法写出解:\(|x|<9\).
- 回答
-
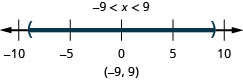
绘制解图并用区间表示法写出解:\(|x|<1\).
- 回答
-
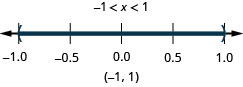
解决\(|5x−6|\leq 4\)。 绘制解图并用区间表示法写出解。
- 解决方案
-
第 1 步。 隔离绝对值表达式。
它是孤立的。\(|5x−6|\leq 4\) 第 2 步。 写出等效的复合不等式。 \(−4\leq 5x−6\leq 4\) 第 3 步。 解决复合不等式。 \(2\leq 5x\leq 10\)
\(\frac{2}{5}\leq x\leq 2\)第 4 步。 绘制解决方案的图表。 
第 5 步。 使用间隔表示法写出解。 \([\frac{2}{5}, 2]\) 支票:
支票留给你。
解决\(|2x−1|\leq 5\)。 绘制解图并用区间表示法写出解:
- 回答
-
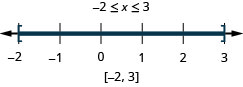
解决\(|4x−5|\leq 3\)。 绘制解图并用区间表示法写出解:
- 回答
-
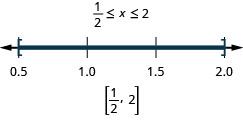
- 隔离绝对值表达式。
- 写出等效的复合不等式。
\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]
- 解决复合不等式。
- 绘制解决方案的图表
- 使用间隔表示法写出解。
用 “大于” 求解绝对值不等式
“大于” 的绝对值不等式会怎样? 再说一遍,我们将看看我们对绝对值的定义。 数字的绝对值是它在数字线上与零的距离。
我们从不平等开始\(|x|\leq 5\)。 我们看到,数字线上距离小于或等于零到五的数字是\(−5\)和 5,所有介于和 5 之间的\(−5\)数字都是(图\(\PageIndex{4}\))。
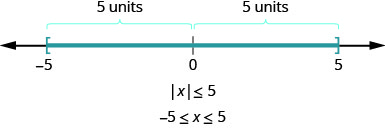
现在我们要看看不平等性\(|x|\geq 5\)。 与零的距离大于或等于五的数字在哪里?
同样,\(−5\)和 5 都是从零开始的五个单位,因此包含在解中。 与零的距离大于五个单位的数字在数字行上将小于\(−5\)或大于 5(图\(\PageIndex{5}\))。
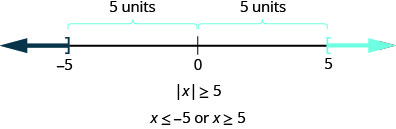
更一般地说,我们可以看出 if\(|u|\geq a\)、then\(u\leq −a\) 或\(u\leq a\)。 见图。
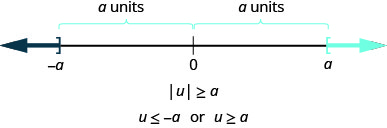
此处总结了此结果。
对于任何代数表达式 u 和任何正实数 a
\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]
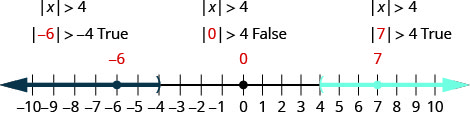
解决\(|x|>4\)。 绘制解图并用区间表示法写出解。
- 解决方案
-
\(|x|>4\) 写下等效的不等式。 \(x<−4\)或\(x>4\) 绘制解决方案的图表。 
使用间隔表示法写出解。 \((−\inf ,−4)\cup (4,\inf )\) 查看: 要进行验证,请检查显示解决方案的数字行的每个部分中的一个值。 选择诸如 −6、−6、0 和 7 之类的数字。
解决\(|x|>2\)。 绘制解图并用区间表示法写出解。
- 回答
-
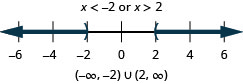
解决\(|x|>1\)。 绘制解图并用区间表示法写出解。
- 回答
-
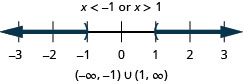
解决\(|2x−3|\geq 5\)。 绘制解图并用区间表示法写出解。
- 解决方案
-
\(|2x−3|\geq 5\) 第 1 步。 隔离绝对值表达式。 它是孤立的。 第 2 步。 写出等效的复合不等式。 \(2x−3\leq −5\)或\(2x−3\geq 5\) 第 3 步。 解决复合不等式。 \(2x\leq −2\)或者\(2x\geq 8\)
\(x\leq −1\)或\(x\geq 4\)第 4 步。 绘制解决方案的图表。 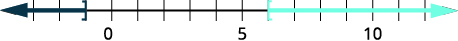
第 5 步。 使用间隔表示法写出解。 \((−\inf ,−1]\cup [4,\inf )\) 支票:
支票留给你。
解决\(|4x−3|\geq 5\)。 绘制解图并用区间表示法写出解。
- 回答
-
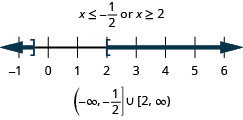
解决\(|3x−4|\geq 2\)。 绘制解图并用区间表示法写出解。
- 回答
-
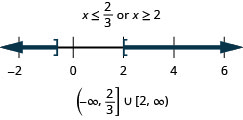
- 隔离绝对值表达式。
- 写出等效的复合不等式。
\ [\ begin {array}
{ll} {|u| >a} & {\ quad\ text {相当于}} & {u<−a\ quad\ text {或}
\ quad u>a}\\ {|u|\ geq a} & {\ quad\ text {或}\ quad u\ geq a}
\\ {|u| >a} & {\ quad\ text {相当于}} & {u<−a\ quad\ text {或}
\ quad u>a}\\ {|u|\ geq a} & {\ quad\ text {或}\ quad u\ geq a}
\\\nonumber\ end {array}\] - 解决复合不等式。
- 绘制解决方案的图表
- 使用间隔表示法写出解。
使用绝对值求解应用程序
绝对值不等式通常用于制造过程。 商品必须以接近完美的规格制成。 通常,允许的规格差异有一定的容差。 如果与规格的差异超过容差,则该商品将被拒收。
\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]
机器所需杆的理想直径为 60 mm。 实际直径可能与理想直径之间有\(0.075\) mm 的差异。 在不导致棒材被拒收的情况下,客户可以接受哪种直径范围?
- 解决方案
-
\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)
机器所需杆的理想直径为 80 mm。 实际直径可能与理想直径相差 0.009 mm。 在不导致棒材被拒收的情况下,客户可以接受哪种直径范围?
- 回答
-
杆的直径可以在 79.991 到 80.009 毫米之间。
机器所需杆的理想直径为 75 mm。 实际直径可能与理想直径相差 0.05 mm。 在不导致棒材被拒收的情况下,客户可以接受哪种直径范围?
- 回答
-
杆的直径可以介于 74.95 和 75.05 毫米之间。
访问此在线资源,获取有关求解线性绝对值方程和不等式的更多指导和练习。
- 求解线性绝对值方程和不等式
关键概念
- 绝对值数字
的绝对值是它在数字线上距离 0 的距离。
数字 n 的绝对值写成所有数字\(|n|\)的\(|n|\geq 0\) and。
绝对值始终大于或等于零。 - 绝对值方程
对于任何代数表达式 u 和任何正实数 a,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\)
请记住绝对值不能是负数。 - 如何求解绝对值方程
- 隔离绝对值表达式。
- 写出等效方程式。
- 求解每个方程。
- 检查每种解决方案。
- 具有两个绝对值的方程
对于任何代数表达式 u 和 v,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\) - 带\(<\)或的绝对值不等式\(\leq\)
对于任何代数表达式 u 和任何正实数 a,
\(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\) - 如何用\(<\)或求解绝对值不等式\(\leq\)
- 隔离绝对值表达式。
- 写出等效的复合不等式。
\(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\) - 解决复合不等式。
- 绘制解决方案的图表
- 使用间隔表示法写出解
- 带\(>\)或的绝对值不等式\(\geq\)
对于任何代数表达式 u 和任何正实数 a,
\(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\) - 如何用\(>\)或求解绝对值不等式\(\geq\)
- 隔离绝对值表达式。
- 写出等效的复合不等式。
\(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\) - 解决复合不等式。
- 绘制解决方案的图表
- 使用间隔表示法写出解


