2.8E：练习

Last updated
Save as PDF

Page ID: 204244

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

练习成就完美

求解绝对值方程

在以下练习中，求解。

1. a.$|x|=6$ b.$|y|=−3$ c.$|z|=0$

2. a.$ |x|=4$ b.$|y|=−5$ c.$|z|=0$

回答: a.$x=4,x=−4$ b. 没有解决方案 c.$z=0$

3. a.$|x|=7$ b.$|y|=−11$ c.$|z|=0$

4. a.$|x|=3$ b.$|y|=−1$ c.$|z|=0$

回答: a.$x=3,x=−3$ b. 没有解决方案 c.$z=0$

5。 $|2x−3|−4=1$

6。 $|4x−1|−3=0$

回答: $x=1, \,x=−\frac{1}{2}$

7。 $|3x−4|+5=7$

8。 $|4x+7|+2=5$

回答: $x=−1, \,x=−\frac{5}{2}$

9。 $4|x−1|+2=10$

10。 $3|x−4|+2=11$

回答: $x=7, \,x=1$

11。 $3|4x−5|−4=11$

12。 $3|x+2|−5=4$

回答: $x=1, \,x=−5$

13。 $−2|x−3|+8=−4$

14。 $−3|x−4|+4=−5$

回答: $x=7, \,x=1$

15。 $|34x−3|+7=2$

16。 $|35x−2|+5=2$

回答: 没有解决办法

17。 $|12x+5|+4=1$

18。 $|14x+3|+3=1$

回答: 没有解决办法

19。 $|3x−2|=|2x−3|$

20。 $|4x+3|=|2x+1|$

回答: $x=−1, \,x=−\frac{2}{3}$

21。 $|6x−5|=|2x+3|$

22。 $|6−x|=|3−2x|$

回答: $x=−3, \,x=3$

用 “小于” 求解绝对值不等式

在以下练习中，求解每个不等式。绘制解图并用区间表示法写出解。

23。 $|x|<5$

24。 $|x|<1$

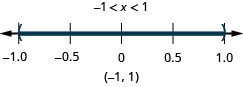
回答: $解为负 1 小于 x，后者小于 1。数字线显示负数 1 处的空心圆圈，1 处的空心圆圈以及圆圈之间的阴影。括号内的间隔表示法是负数 1 到 1。$

25。 $|x|\leq 8$

26。 $|x|\leq 3$

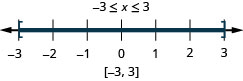
回答: $解为负 3 小于或等于 x，后者小于或等于 3。数字线在负 3 处显示一个封闭的圆圈，在 3 处显示一个封闭的圆圈，以及两个圆之间的阴影。方括号内的间隔符号为负 3 到 3。$

27。 $|3x−3|\leq 6$

28。 $|2x−5|\leq 3$

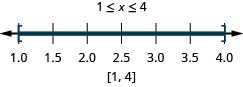
回答: $解为 1 小于或等于 x，后者小于或等于 4。数字线在 1 处显示一个封闭的圆圈，在 4 处显示一个封闭的圆圈，以及两个圆之间的阴影。方括号内的间隔符号为 1 到 4。$

29。 $|2x+3|+5<4$

30。 $|3x−7|+3<1$

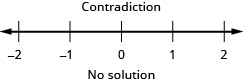
回答: $解决方案是矛盾的。所以，没有解决办法。因此，没有图表、数字线或间隔符号。$

31。 $|4x−3|<1$

32。 $|6x−5|<7$

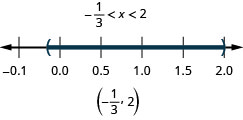
回答: $解为负三分之一小于 x，后者小于 2。数字线在负一半处显示一个空心圆，在 2 处显示一个空圆，圆圈之间的阴影。括号内的间隔表示法为负三分之一到 2。$

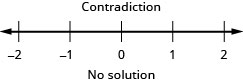
33。 $|x−4|\leq −1$

34。 $|5x+1|\leq −2$

回答: $解决方案是矛盾的。所以，没有解决办法。因此，没有图表、数字线或间隔符号。$

用 “大于” 求解绝对值不等式

在以下练习中，求解每个不等式。绘制解图并用区间表示法写出解。

35。 $|x|>3$

36。 $|x|>6$

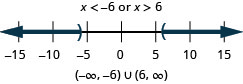
回答: $解是 x 小于负 6 或 x 大于 6。数字线在负数 6 处显示一个空心圆圈，左边有阴影，6 处有一个空心圆圈，右边有阴影。区间表示法是圆括号内负无穷大到负 6 和括号内的 6 到无穷大的并集$

37。 $|x|\geq 2$

38。 $|x|\geq 5$

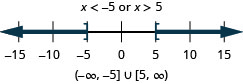
回答: $解是 x 小于负 5 或 x 大于 5。数字线显示一个负数 5 处的空心圆圈，左边有阴影，5 处有一个空心圆圈，右边有阴影。区间表示法是圆括号内负无穷大到负 5 和括号内的 5 到无穷大的并集。$

39。 $|3x−8|>−1$

40。 $|x−5|>−2$

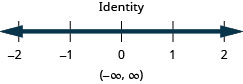
回答: $解决方案是身份。它在数字线上的解为所有值的阴影。区间表示法中的解是圆括号内的负无穷大到无穷大。$

41。 $|3x−2|>4$

42。 $|2x−1|>5$

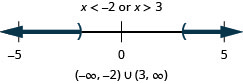
回答: $解是 x 小于负 2 或 x 大于 3。数字线在负 2 处显示一个空心圆，左边有阴影，右边是阴影 3 处有一个空心圆圈，右边是阴影。区间表示法是圆括号内负无穷大与负 2 的并集，括号内的 3 到无穷大的并集。$

43。 $|x+3|\geq 5$

44。 $|x−7|\geq 1$

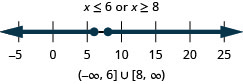
回答: $解是 x 小于或等于 6 或 x 大于或等于 8。数字线在 6 处显示一个封闭的圆圈，左边有阴影，8 处有一个封闭的圆圈，右边是阴影。间隔表示法是圆括号和方括号内负无穷大到 6 的并集，以及方括号和括号内的 8 到无穷大的并集。$

45。 $3|x|+4\geq 1$

46。 $5|x|+6\geq 1$

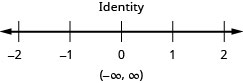
回答: $解决方案是身份。它在数字线上的解为所有值的阴影。区间表示法中的解是圆括号内的负无穷大到无穷大。$

在以下练习中，求解。对于每个不等式，还要绘制解图并用区间表示法写出解。

47。 $2|x+6|+4=8$

48。 $|3x−4|\geq 2$

回答: $x=4,x=27$

49。 $|6x−5|=|2x+3|$

50。 $|4x−3|<5$

回答: $x=3,x=2$

51。 $|2x−5|+2=3$

52。 $|3x+1|−3=7$

回答: $x=3,x=−\frac{11}{3}$

53。 $|7x+2|+8<4$

54。 $5|2x−1|−3=7$

回答: $x=\frac{3}{2},x=−\frac{1}{2}$

55。 $|x−7|>−3$

56。 $|8−x|=|4−3x|$

回答: $解决方案是身份。它在数字线上的解为所有值的阴影。区间表示法中的解是圆括号内的负无穷大到无穷大。$

使用绝对值求解应用程序

在以下练习中，求解。

57。理想情况下，养鸡场每天生产 200,000 个鸡蛋。但是这个总数可能相差多达25,000个鸡蛋。农场的最大和最低预期产量是多少？

58。理想情况下，有机果汁装瓶商每天可生产 215,000 瓶。但是这个总量可能相差多达7,500瓶。装瓶公司的最大和最低预期产量是多少？

回答: 最低至最高预期产量为207,500至2,22.5万瓶

59。为了确保遵守法律，米格尔经常将玉米饼的重量超出0.5克。他刚刚收到一份报告，告诉他，使用这种做法，他每年可能损失多达100,000美元。他现在计划购买新设备，保证玉米饼的厚度在0.005英寸以内。如果玉米饼的理想厚度为 0.04 英寸，则可以保证玉米饼的厚度是多少？

60。在 Lilly's Bakery，一条面包的理想重量为 24 盎司。根据法律，实际重量可能与理想重量相差 1.5 盎司。在不导致面包店被罚款的情况下，检查员可以接受什么范围的重量？

回答: 可接受的重量为 22.5 到 25.5 盎司。

写作练习

61。写一个数字的绝对值的图形描述

62。用你自己的话说，解释如何解决绝对价值不等式，$|3x−2|\geq 4$。

回答: 答案会有所不同。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

$此表有四列五行。第一行是标题，它会将每列标记为 “我可以...”、“自信”、“有帮助” 和 “不我不明白！” 在第 2 行中，“我能” 是求解绝对值方程。在第 3 行中，我能用 “小于” 求解绝对值不等式。在第 4 行中，我能用 “大于” 求解绝对值不等式。在第 5 行中，“我能” 是用绝对值求解应用程序。$

b. 关于你对本部分的掌握程度，这份清单告诉了你什么？你会采取哪些措施来改进？