第 2 章复习练习

章节复习练习

使用通用策略求解线性方程

使用求解线性方程的通用策略求解方程

在以下练习中，确定每个数字是否是方程的解。

1。 \(10x−1=5x,\quad x= \frac{1}{5}\)

2。 \(−12n+5=8n,\quad n=−\frac{5}{4}\)

回答

不

在以下练习中，求解每个线性方程。

3。 \(6(x+6)=24\)

4。 \(−(s+4)=18\)

回答

\(s=−22\)所以解决方案集是：\( \{-22\} \)。

5。 \(23−3(y−7)=8\)

6。 \(\frac{1}{3}(6m+21)=m−7\)

回答

\(m=−14\)

7。 \(4(3.5y+0.25)=365\)

8。 \(0.25(q−8)=0.1(q+7)\)

回答

\(q=18\)

9。 \(8(r−2)=6(r+10)\)

10。 \(5+7(2−5x)=2(9x+1)−(13x−57)\)

回答

\(x=−1\)

11。 \((9n+5)−(3n−7)=20−(4n−2)\)

12。 \(2[−16+5(8k−6)]=8(3−4k)−32\)

回答

\(k=\frac{3}{4}\)

对方程进行分类

在以下练习中，将每个方程归类为条件方程、恒等方程或矛盾，然后陈述解。

13。 \(17y−3(4−2y)=11(y−1)+12y−1\)

14。 \(9u+32=15(u−4)−3(2u+21)\)

回答

矛盾；没有解决办法

15。 \(−8(7m+4)=−6(8m+9)\)

使用分数或十进制系数求解方程

在以下练习中，求解每个方程。

16。 \(\frac{2}{5}n−\frac{1}{10}=\frac{7}{10}\)

回答

\(n=2\)

17。 \(\frac{3}{4}a−\frac{1}{3}=\frac{1}{2}a+\frac{5}{6}\)

18。 \(\frac{1}{2}(k+3)=\frac{1}{3}(k+16)\)

回答

\(k=23\)

19。 \(\frac{5y−1}{3}+4=\frac{-8y+4}{6}\)

20。 \(0.8x−0.3=0.7x+0.2\)

回答

\(x=5\)

21。 \(0.10d+0.05(d−4)=2.05\)

使用问题解决策略

对单词问题使用问题解决策略

在以下练习中，使用问题解决策略解决单词问题。

22。 参加音乐会的人中有四分之三是儿童。 如果有87个孩子，那么参加音乐会的总人数是多少？

回答

有 116 个人。

23。 乐队里有九位萨克斯管演奏者。 萨克斯管演奏者的数量比大号演奏者数量少一倍。 找出大号演奏者的数量。

解决数字词问题

在以下练习中，解决每个数字字的问题。

24。 一个数字和三的总和为四十一。 找到号码。

回答

38

25。 一个数字比另一个数字少九个。 他们的总和为负二十七。 找到数字。

26。 一个数字比另一个数字多四倍。 他们的总和为负十三。 找到数字。

回答

\(−3,−10\)

27。 两个连续整数的总和为\(−135\)。 找到数字。

28。 找出三个连续的偶数整数，总和为 234。

回答

76、78、80

29。 找出三个连续的奇数整数，其总和为 51。

30。 Koji 的储蓄账户里有 5,502 美元。 这比他支票账户金额的六倍少了30美元。 Koji 的支票账户里有多少钱？

回答

922 美元

求解百分比应用程序

在以下练习中，翻译并求解。

31。 250 中的 67% 是多少？

32. 哪个数字的 12.5% 是 20？

回答

\(160\)

33。 125 中的多少百分比是 150？

在以下练习中，求解。

34。 迪诺午餐的账单是19.45美元。 他想把账单总额的20％留作小费。 小费应该是多少？

回答

\($3.89\)

35。 多洛雷斯以350美元的价格购买了一张婴儿床。 销售价格为原价的40％。 婴儿床的原价是多少？

36。 Jaden 每月的收入为 2,680 美元。 他每月支付938美元的租金。 他月薪中有多少百分比用于租金？

回答

\(35%\)

37。 安吉尔的年薪从55,400美元提高到56,785美元。 找出百分比变化。

38。 罗文娜的每月汽油账单从上个月的83.75美元下降到本月的56.95美元。 找出百分比变化。

回答

\(32%\)

39。 Emmett 购买了一双特价鞋，比原价 138 美元低了 40%。 查找 ⓐ 折扣金额和 ⓑ 销售价格。

40。 莱西以95美元的价格买了一双靴子。 这双靴子的原价为200美元。 查找 ⓐ 折扣金额和 ⓑ 折扣率。 （如果需要，四舍五入到最接近的百分之一的十分之一。）

回答

ⓐ\($105\) ⓑ\(52.5%\)

41。 Nga 和 Lauren 在跳蚤市场以 50 美元的价格买了一个箱子。 他们重新完成了它，然后增加了350％的加价。 找到 ⓐ 加价金额和 ⓑ 标价。

解决简单利息申请

在以下练习中，求解。

42。 温斯顿将3,294美元存入银行账户，利率为2.6％ 五年内赚了多少利息？

回答

\($428.22\)

43。 莫伊拉从祖父那里借了4,500美元来支付她上大学第一年的费用。 三年后，她偿还了4,500美元外加243美元的利息。 利率是多少？

44。 海梅的冰箱贷款声明说，他将为四年期贷款支付1,026美元的利息，利息为13.5％。 Jaime 借了多少钱买了冰箱？

回答

\($1,900\)

求解特定变量的公式

求解特定变量的公式

在以下练习中，求解指定变量的公式。

45。 求解 L
\(V=LWH\) 的公式。

46。 求解公
\(A=\frac{1}{2}d_1d_2\)式\(d_2\)。

回答

\(d_2=\frac{2A}{d_1}\)

47。 求解 t
\(h=48t+\frac{1}{2}at^2\) 的公式。

48。 求解 y 的公式
4x−3y=12。

回答

\(y=\frac{4x}{3}−4\)

使用公式求解几何应用程序

在以下练习中，使用几何公式求解。

49。 面积为 67.567.5 平方米、底部为 9 米的三角形的高度是多少？

50。 直角三角形中最小角度的测量值比下一个较大角度的测量值小 45°45°。 找出所有三个角度的测量值。

回答

\(22.5°,\; 67.5°,\; 90°\)

51。 三角形的周长为 97 英尺。 三角形的一侧比最小的一边多十一英尺。 第三边是六英尺，是最小边的两倍多。 找出所有边的长度。

52。 找出斜边的长度。

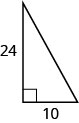
回答

\(26\)

53。 找出缺失边的长度。 如有必要，四舍五入到最接近的十分之一。

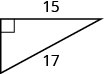
54。 如图所示，塞尔吉奥需要连接一根电线才能将天线固定在他家的屋顶上。 天线高八英尺，塞尔吉奥有 10 英尺的电线。 他能在离天线底部多远的地方连接电线？ 如有必要，请近似至最接近的十分之一。

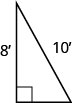
回答

6 英尺

55。 Seong 正在他的车库里搭架子。 架子宽 36 英寸，高 15 英寸。 如图所示，他想在背面放一个对角支架以稳定架子。 支架应该有多长？

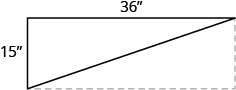
56。 矩形的长度比宽度多 12 厘米。 周长为 74 厘米。 找出长度和宽度。

回答

\(24.5\)厘米，\(12.5\)厘米

57。 矩形的宽度是长度的三倍以上。 周长为 96 英寸。 找出长度和宽度。

58。 三角形的周长为 35 英尺。 三角形的一边比第二边长五英尺。 第三边比第二边长三英尺。 找出每边的长度。

回答

9 英尺、14 英尺、12 英尺

求解混合和均匀运动应用程序

解决硬币单词问题

在以下练习中，求解。

59。 保莱特有140美元的5美元和10美元的钞票。 10美元的钞票数量少于5美元钞票数量的两倍。 她每人有多少个？

60。 Lenny 有 3.69 美元的便士、毛钱和季度。 便士的数量比硬币的数量多三分之一。 季度数是硬币数的两倍。 他每枚硬币有多少？

回答

九便士、六角钱、12 个季度

解决票证和邮票字词问题

在以下练习中，解决每张票或邮票单词的问题。

61。 篮球比赛的门票为学生2美元，成人5美元。 学生人数为三人，少于成人人数的十倍。 门票销售的总收入为619美元。 每张门票售出了多少张？

62. 爵士乐队音乐会共售出125张门票，总额为1,022美元。 学生门票每张花费6美元，普通门票每张花费10美元。 每种门票售出了多少张？

回答

57 名学生，68 名成人

63。 Yumi 花了 34.15 美元购买邮票。 她购买的0.56美元的邮票数量比0.41美元邮票数量少了10张。 她每种都买了多少？

解决混词问题

在以下练习中，求解。

64。 Marquese 正在用葡萄干和坚果制作 10 磅的混合物。 葡萄干每磅的价格为3.45美元，坚果的价格为每磅7.95美元。 Marquese 应该用多少磅的葡萄干和多少磅的坚果作为混合物，每磅花费 6.96 美元？

回答

\(2.2\)磅葡萄干，\(7.8\)磅坚果

65。 Amber 想在厨房柜台的后挡板上铺瓷砖。 她需要 36 平方英尺的瓷砖。 她将使用每平方英尺花费8美元的基本瓷砖和每平方英尺花费20美元的装饰瓷砖。 她应该使用每块瓷砖多少平方英尺，这样后挡板的总成本才能达到每平方英尺10美元？

66。 恩里克借了23,500美元买车。 他向叔叔借的4,500美元向叔叔支付2％的利息，其余的则向银行支付11.5％的利息。 对于总额为23,500美元，他支付的平均利率是多少？ （将答案四舍五入到最接近的百分之一的十分之一。）

回答

\(9.7%\)

求解均匀运动应用程序

在以下练习中，求解。

67。 当 Gabe 从萨克拉曼多开车去雷丁时，他花了 2.2 个小时。 艾尔莎要花两个小时才能开同样的距离。 艾尔莎的速度比加布的速度快七英里/小时。 找出加布的速度和艾尔莎的速度。

68。 Louellen 和 Tracy 在芝加哥和纳什维尔之间的路上的一家餐馆见面。 Louellen 离开芝加哥，开车 3.2 小时前往纳什维尔。 特雷西离开了纳什维尔，开了4个小时前往芝加哥，速度比Louellen的速度快一英里/小时。 芝加哥和纳什维尔之间的距离为 472 英里。 找出 Louellen 的速度和 Tracy 的速度。

回答

Louellen 65 英里/小时，Tracy 66 m

69。 两辆公共汽车同时离开阿马里洛。 阿尔伯克基公交车在I-40公路上以每小时72英里的速度向西行驶，俄克拉荷马城的公交车以每小时78英里的速度在I-40上向东行驶。 他们相隔 375 英里需要多少小时？

70。 凯尔在船上游划了50分钟。 他花了 30 分钟才划回下游。 他向上游行驶的速度比下游的速度每小时慢两英里。 查找 Kyle 的上游和下游速度。

回答

上游 3 英里/小时，下游 5 英里/小时

71。 6:30，德文离开家，在平坦的道路上骑自行车直到 7:30。 然后她开始上坡骑行，一直骑到 8:00。 她总共骑了 15 英里。 她在平坦道路上的速度比上坡时速快三英里/小时。 在平坦的道路上找到德文郡的速度，然后上坡骑行。

72。 安东尼从纽约市开车前往巴尔的摩，距离为192英里。 他于 3:45 离开，交通繁忙直到 5:30。 接下来的路段交通很少，他在 7:30 到达。 他在轻型交通中的速度为每小时四英里，是交通繁忙时速度的两倍多。 查找安东尼在交通繁忙和交通不便时的行驶速度。

回答

交通繁忙 32 英里每小时，轻度交通 66 英里每小时

求解线性不等式

在数字线上绘制不等式图

在以下练习中，在数字行上绘制不等式并用间隔符号书写。

73。 \(x<−1\)

74。 \(x\geq −2.5\)

回答

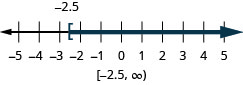
75。 \(x\leq \frac{5}{4}\)

76。 \(x>2\)

回答

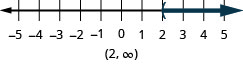
77。 \(−2<x<0\)

78。 \(-5\leq x<−3\)

回答

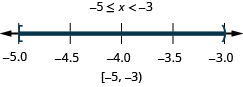
79。 \(0\leq x\leq 3.5\)

求解线性不等式

在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

80。 \(n−12\leq 23\)

回答

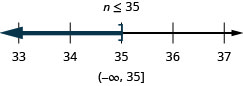
81。 \(a+\frac{2}{3}\geq \frac{7}{12}\)

82。 \(9x>54\)

回答

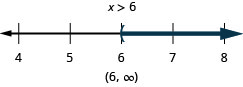
83。 \(\frac{q}{−2}\geq −24\)

84。 \(6p>15p−30\)

回答

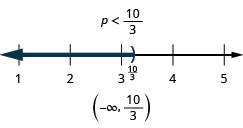
85。 \(9h−7(h−1)\leq 4h−23\)

86。 \(5n−15(4−n)<10(n−6)+10n\)

回答

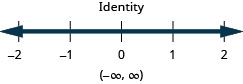
87。 \(\frac{3}{8}a−\frac{1}{12}a>\frac{5}{12}a+\frac{3}{4}\)

将单词转换为不等式并求解

在以下练习中，翻译并求解。 然后用区间表示法在数字行上写下解和图形。

88。 比\(z\)最多多五个 19。

回答

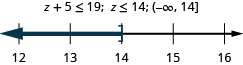
89。 小于三个至少\(c\)为 360。

90。 九次\(n\)超过 42 次。

回答

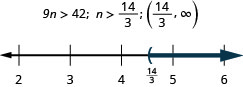
91。 负两倍\(a\)不超过八次。

求解具有线性不等式的应用程序

在以下练习中，求解。

92。 朱莉安每周为家人准备的食物预算为231美元。 如果她计划在一周的七天中每天都用相同的金额预算，那么她每天最多可以花在食物上的金额是多少？

回答

每天 33 美元

93。 罗杰里奥画水彩画。 他在艺术用品商店收到了一张100美元的礼品卡，想用它来购买12英寸×16英寸的画布。 每幅画布的价格为10.99美元。 他可以使用礼品卡购买的最大画布数量是多少？

94。 Briana在另一个城市获得了销售工作。 报价为42,500美元，再加上她总销售额的8％。 为了物有所值，Briana的年薪必须至少为66,500美元。 她的总销售额需要多少才能搬家？

回答

至少 30 万美元

95。 蕾妮的汽车每月花费195美元，外加每英里0.09美元。 蕾妮能开多少英里才能使她每月的汽车开支不超过250美元？

96。 科斯塔是一名会计师。 在纳税季节，他收取125美元的简单纳税申报单。 他购买软件、租用办公室和做广告的费用为6,000美元。 如果他想赚取至少8,000美元的利润，他必须填写多少纳税申报表？

回答

至少 112 个工作岗位

97。 珍娜正计划和她的三个朋友一起度过一个为期五天的度假胜地。 她将花费279美元的机票，300美元的食物和娱乐费用，以及每天65美元的酒店份额。 她有550美元的度假积蓄，在叔叔的摄影工作室当助手每小时可以赚25美元。 她必须工作多少小时才能有足够的钱休假？

求解复合不等式

用 “and” 求解复合不等式

在以下每个练习中，求解每个不等式，绘出解图，然后用区间表示法写出解。

98。 \(x\leq 5\)和\(x>−3\)

回答

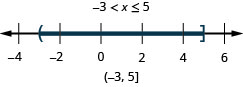
99。 \(4x−2\leq 4\)和\(7x−1>−8\)

100。 \(5(3x−2)\leq 5\)和\(4(x+2)<3\)

回答

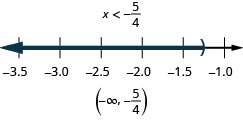
101。 \(34(x−8)\leq 3\)和\(15(x−5)\leq 3\)

102。 \(34x−5\geq −2\)和\(−3(x+1)\geq 6\)

回答

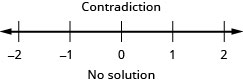
103。 \(−5\leq 4x−1<7\)

用 “或” 求解复合不等式

在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

104。 \(5−2x\leq −1\)或者\(6+3x\leq 4\)

回答

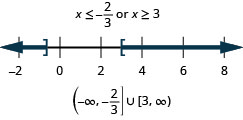
105。 \(3(2x−3)<−5\)或者\(4x−1>3\)

106。 \(34x−2>4\)或者\(4(2−x)>0\)

回答

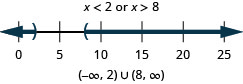
107。 \(2(x+3)\geq 0\)或者\(3(x+4)\leq 6\)

108。 \(12x−3\leq 4\)或者\(13(x−6)\geq −2\)

回答

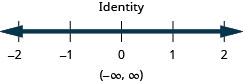
使用复合不等式求解应用程序

在以下练习中，求解。

109。 利亚姆正在和他的妹妹奥德里玩数字游戏。 利亚姆正在想一个数字，想让奥德里猜出来。 她的号码超过三倍的五倍在2到32之间。 写一个复合不等式，显示利亚姆可能想到的数字范围。

110。 Elouise 正在她的后院建造一个矩形花园。 花园的长度为 12 英尺。 花园的周长必须至少为 36 英尺且不超过 48 英尺。 使用复合不等式来查找花园宽度的值范围。

回答

\(6\leq w\leq 12\)

求解绝对值不等式

求解绝对值方程

在以下练习中，求解。

111。 \(|x|=8\)

112。 \(|y|=−14\)

回答

没有解决办法

113。 \(|z|=0\)

114。 \(|3x−4|+5=7\)

回答

\(x=2,x=\frac{2}{3}\)

115。 \(4|x−1|+2=10\)

116。 \(−2|x−3|+8=−4\)

回答

\(x=9,x=−3\)

117。 \(|12x+5|+4=1\)

118。 \(|6x−5|=|2x+3|\)

回答

\(x=2,x=14\)

用 “小于” 求解绝对值不等式

在以下练习中，求解每个不等式。 绘制解图并用区间表示法写出解。

119。 \(|x|\leq 8\)

120。 \(|2x−5|\leq 3\)

回答

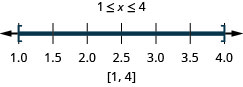
121。 \(|6x−5|<7\)

122。 \(|5x+1|\leq −2\)

回答

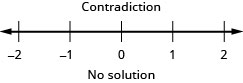
用 “大于” 求解绝对值不等式

在以下练习中，求解。 绘制解图并用区间表示法写出解。

123。 \(|x|>6\)

124。 \(|x|\geq 2\)

回答

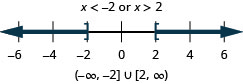
125。 \(|x−5|>−2\)

126。 \(|x−7|\geq 1\)

回答

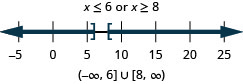
127。 \(3|x|+4\geq 1\)

使用绝对值求解应用程序

在以下练习中，求解。

128。 精酿啤酒酿造商每天需要 215,000 瓶。 但是这个总数可能相差多达5,000瓶。 装瓶公司的最大和最低预期使用量是多少？

回答

预期的最小到最大使用量为 210,000 至 22 万瓶

129。 在 Fancy Grocery，一条面包的理想重量为 16 盎司。 根据法律，实际重量可能与理想重量相差 1.5 盎司。 在不导致面包店被罚款的情况下，检查员可以接受什么范围的重量？

练习测试

在以下练习中，求解每个方程。

1。 \(−5(2x+1)=45\)

回答

\(x=−5\)

2。 \(\frac{1}{4}(12m+28)=6+2(3m+1)\)

3。 \(8(3a+5)−7(4a−3)=20−3a\)

回答

\(a=41\)

4。 \(0.1d+0.25(d+8)=4.1\)

5。 \(14n−3(4n+5)=−9+2(n−8) \)

回答

矛盾；没有解决办法

6。 \(3(3u+2)+4[6−8(u−1)]=3(u−2)\)

7。 \(\frac{3}{4}x−\frac{2}{3}=\frac{1}{2}x+\frac{5}{6}\)

回答

\(x=6\)

8。 \(|3x−4|=8\)

9。 \(|2x−1|=|4x+3|\)

回答

\(x=−2,x=−13\)

10。 求解 y
\(x+2y=5\) 的公式。

在以下练习中，在数字行上绘制不等式并用间隔符号书写。

11。 \(x\geq −3.5\)

回答

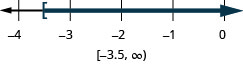
12。 \(x<\frac{11}{4}\)

13。 \(−2\leq x<5\)

回答

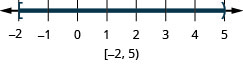
在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

14。 \(8k\geq 5k−120\)

15。 \(3c−10(c−2)<5c+16\)

回答

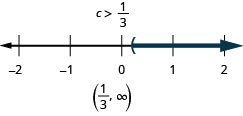
16。 \(\frac{3}{4}x−5\geq −2\)和\(−3(x+1)\geq 6\)

17。 \(3(2x−3)<−5\)或者\(4x−1>3\)

回答

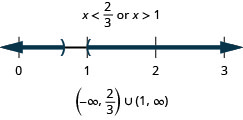
18。 \(\frac{1}{2}x−3\leq 4\)或者\(\frac{1}{3}(x−6)\geq −2\)

19。 \(|4x−3|\geq 5\)

回答

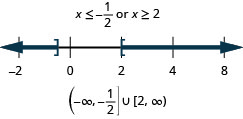
在以下练习中，转换为方程或不等式并求解。

20。 小于两倍的四个 x 等于 16。

21。 找出缺失边的长度。

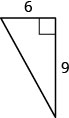
回答

\(10.8\)

22。 一个数字是四比另一个数字的两倍多。 他们的总和是\(−47\)。 找到数字。

23。 两个连续奇数整数的总和为\(−112\)。 找到数字。

回答

\(−57,−55\)

24。 马库斯以626.50美元的价格购买了一台电视机的原价为895美元。 查找 ⓐ 折扣金额和 ⓑ 折扣率。

25。 博尼塔的口袋里有2.95美元的毛钱和四分之一。 如果她的硬币比四分之一多五角钱，那么她每枚硬币有多少钱？

回答

12 毛钱，四分之七

26。 Kim 正在用果汁和苏打水冲泡八加仑的冲击力。 果汁的价格为每加仑6.04美元，苏打水的价格为每加仑4.28美元。 她应该用多少果汁和多少苏打水，这样拳头每加仑的价格为5.71美元？

27。 三角形的一个角度的度量是最小角度的两倍。 第三个角度的测量值是最小角度的三倍。 找出所有三个角度的测量值。

回答

\(30°,60°,90°\)

28。 矩形的长度比宽度的四倍多五英尺。 周长为 60 英尺。 找到矩形的尺寸。

29。 两架飞机同时离开达拉斯。 一个人以每小时 428 英里的速度向东行驶。 另一架飞机以每小时 382 英里的速度向西飞行。 他们相隔 2,025 英里需要多少小时？

回答

\(2.5\)小时

30。 莱昂从辛辛那提的房子开车到他姐姐在克利夫兰的房子里，距离252英里。 他花了好\(4\frac{1}{2}\)几个小时。 在最初的半小时里，他交通繁忙，其余时间他的速度为每小时五英里，不到交通繁忙时速度的两倍。 他在交通繁忙时的速度是多少？

31。 萨拉有1,000美元的预算为她的音乐剧团的18名成员购买服装。 她最多可以花多少钱购买每套服装？

回答

每套服装最多55.56美元。