Skip to main content
Global

2.7：求解复合不等式

  1. Last updated
  2. Save as PDF
  • Page ID
    204303

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 用 “and” 求解复合不等式
    • 用 “或” 求解复合不等式
    • 求解具有复合不等式的应用程序

    在开始之前，请参加这个准备测验。

    1. 简化：\(\frac{2}{5}(x+10)\)。
      如果你错过了这个问题，请查看 [链接]。
    2. 简化：\(−(x−4)\)。
      如果你错过了这个问题，请查看 [链接]。

    用 “and” 求解复合不等式

    既然我们知道如何解决线性不等式，下一步就是研究复合不等式。 复合不等式由两个由单词 “and” 或 “or” 相连的不等式组成。 例如，以下是复合不等式。

    \[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]

    复合不等式

    复合不等式由两个由单词 “and” 或 “or” 相连的不等式组成。

    求解复合不等式意味着找到使复合不等式成为真实陈述的变量的所有值。 我们使用与求解线性不等式相同的技术来求解复合不等式。 我们分别求解每个不等式，然后考虑两个解决方案。

    要用 “and” 一词求解复合不等式，我们要寻找所有能使两个不等式都成真的数字。 要用 “或” 一词求解复合不等式，我们要寻找所有能使任一不等式都成真的数字。

    让我们从带有 “and” 的复合不等式开始。 我们的解决方案将是两个不等式的解的数字，即两个不等式的交集。 假设两条街道的交叉点（街道重叠的部分）属于两条街道。

    该图是两条街道的插图，其交叉路口有阴影

    为了找出 “和” 复合不等式的解，我们查看每个不等式的图，然后找到属于两个图的数字，即图形重叠的地方。

    对于复合不\(x>−3\)等式\(x\leq 2\)，我们绘制每个不等式的图形。 然后，我们寻找图表 “重叠” 的位置。 两张图上带有阴影的数字将在复合不等式解的图上加上阴影。 参见图\(\PageIndex{1}\)。

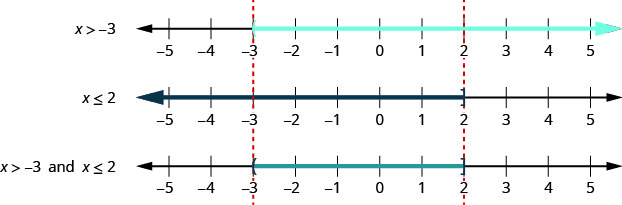
    该图显示 x 的图大于负 3，左括号为负 3，右侧为阴影；x 的图形小于或等于 2，方括号为 2，阴影位于左侧；x 的图大于负 3，x 小于或等于 2，带有左括号在负 3 处，右括号为 2，阴影介于负 3 和 2 之间。 负数 3 和 2 在每个数字行上用行标记。
    图\(\PageIndex{1}\)

    我们可以看到，在前两张图中，\(−3\)和之间的数字\(2\)都是阴影的。 然后，它们将在解决方案图上加上阴影。

    \(−3\)该数字在第一张图上没有阴影，因此由于两张图上都没有阴影，因此它不包含在解图中。

    数字二在第一张和第二张图上都有阴影。 因此，它会在解图上加上阴影。

    在接下来的示例中，我们将以这种方式展示我们的解决方案。

    示例\(\PageIndex{1}\)

    求解\(6x−3<9\)和\(2x+7\geq 3\)。 绘制解图并用区间表示法写出解。

    回答
      \(6x−3<9\) 和 \(2x+9\geq 3\)
    第 1 步。 解决每个
    不等式。    		 \(6x−3<9\)   \(2x+9\geq 3\)
      \(6x<12\)   \(2x\geq −6\)
      \(x<2\) 和 \(x\geq −3\)
    第 2 步。 绘制每个解决方案的图表。 然后绘制使两个不等式都成真的数字。 最后一张图将显示使两个不等式都成真的所有数字，即前两张图上的阴影数字。 。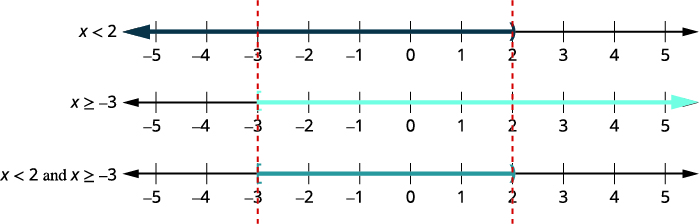
    第 3 步。 用间隔表示法写出解。 \([−3,2)\)
    使两个不等式都成真的所有数字都是复合不等式的解决方案。
    示例\(\PageIndex{2}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(4x−7<9\)和\(5x+8\geq 3\)。

    回答

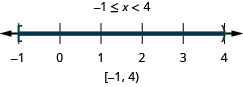
    解为负 1 小于或等于 x，后者小于 4。 在数字线上，它以负1处的封闭圆和4处的空心圆圈显示，封闭圆和空心圆之间有阴影。 在方括号和括号中，它的间隔表示法是负数 1 到 4。

    示例\(\PageIndex{3}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(3x−4<5\)和\(4x+9\geq 1\)。

    回答

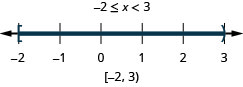
    解为负 2 小于或等于 x，后者小于 3。 在数字线上，它以负2处的封闭圆和3处的空心圆圈显示，封闭圆和空心圆之间有阴影。 在方括号和括号中，它的间隔表示法是负数 2 到 3。

    用 “AND” 求解复合不等式。
    1. 解决每个不等式。
    2. 绘制每个解决方案的图表。 然后绘制使两个不等式都成真的数字的图形。
      这张图显示了复合不等式的解。
    3. 用间隔表示法写出解。
    示例\(\PageIndex{4}\)

    求解\(3(2x+5)\leq 18\)和\(2(x−7)<−6\)。 绘制解图并用区间表示法写出解。

    回答
      \(3(2x+5)\leq 18\) 和 \(2(x−7)<−6\)
    解决每个
    不等式。    		 \(6x+15\leq 18\)   \(2x−14<−6\)
      \(6x\leq 3\)   \(2x<8\)
      \(x\leq \frac{1}{2}\) 和 \(x<4\)
    绘制每个
    解决方案的图表。    		 。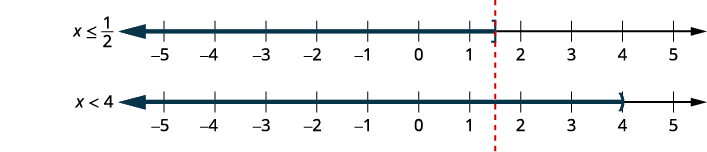
    绘制使两个
    不等式都成真的数字
    。    		 。
    用间隔表示法写出解。
    		 \((−\infty, \frac{1}{2}]\)
    示例\(\PageIndex{5}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(2(3x+1)\leq 20\)和\(4(x−1)<2\)。

    回答

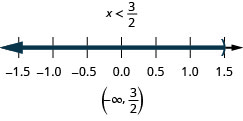
    解决方案是 x 小于三半。 在数字线上，它以三半处的空心圆圈显示，左侧有阴影。 它的间隔表示法是负无穷大到圆括号内的三半。

    示例\(\PageIndex{6}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(5(3x−1)\leq 10\)和\(4(x+3)<8\)。

    回答

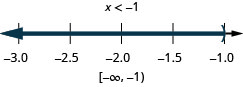
    解是 x 小于负 1。 在数字线上，它以 1 处的空心圆圈显示，左边有阴影。 其间隔表示法在括号内为负无穷大到负 1。

    示例\(\PageIndex{7}\)

    求解\(\frac{1}{3}x−4\geq −2\)和\(−2(x−3)\geq 4\)。 绘制解图并用区间表示法写出解。

    回答
      \(\frac{1}{3}x−4\geq −2\) 和 \(−2(x−3)\geq 4\)
    解决每个不等式。 \(\frac{1}{3}x−4\geq −2\)   \(−2x+6\geq 4\)
      \(\frac{1}{3}x\geq 2\)   \(−2x\geq −2\)
      \(x\geq 6\) 和 \(x\leq 1\)
    绘制每个解决方案的图表。 。。。
    绘制
    使两个不等式都成
    真的数字。    		 。。。
      没有数字可以证明这两个不等式都是正确的。

    这是矛盾的，所以没有解决方案。没有数字可以证明这两个不等式都是正确的。

    这是矛盾的，所以没有解决方案。没有数字可以证明这两个不等式都是正确的。

    这是矛盾的，所以没有解决办法。
    示例\(\PageIndex{8}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(\frac{1}{4}x−3\geq −1\)和\(−3(x−2)\geq 2\)。

    回答

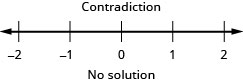
    不平等是矛盾的。 所以，没有解决办法。 因此，没有数字线或间隔符号的图表。

    示例\(\PageIndex{9}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(\frac{1}{5}x−5\geq −3\)和\(−4(x−1)\geq −2\)。

    回答

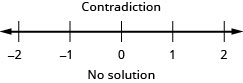
    不平等是矛盾的。 所以，没有解决办法。 因此，没有图表、数字线或间隔符号。

    有时候我们有一个可以写得更简洁的复合不等式。 例如，\(a<x\)和\(x<b\)可以简单地写成，\(a<x<b\)然后我们称之为双不等式。 这两种形式是等效的。

    双重不平等

    双重不等式是一种复合不等式，例如\(a<x<b\)。 它等同于\(a<x\)和\(x<b\)。

    \[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]

    为了解决双不等式，我们对双不等式的所有三个 “部分” 执行相同的运算，目标是将变量隔离在中心。

    示例\(\PageIndex{10}\)

    解决\(−4\leq 3x−7<8\)。 绘制解图并用区间表示法写出解。

    回答
      \(-4 \leq 3x - 7 < 8\)
    在所有三个部分中加上 7。 \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\)
    简化。 \( 3 \le 3x < 15 \)
    将每个部分除以三。 \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \)
    简化。 \( 1 \leq x < 5 \)
    绘制解决方案的图表。 。
    用间隔表示法写出解。 \( [1, 5) \)

    当写成双不等式时\(1\leq x<5\)，很容易看出解是介于一到五之间的数字，包括一，但不包括五。 然后，我们可以像上面那样立即绘制解决方案的图表。

    绘制解图的另一种方法\(1\leq x<5\)是绘制解\(x\geq 1\)和解的图形\(x<5\)。 然后，我们将找到使两个不等式都成真的数字，就像我们在前面的例子中所做的那样。

    示例\(\PageIndex{11}\)

    解决复合不等式。 绘制解图并用区间表示法写出解:\(−5\leq 4x−1<7\).

    回答

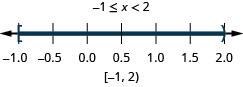
    解为负 1 小于或等于 x，后者小于 2。 它的图形在负1处有一个封闭的圆，在2处有一个空圆，封闭圆和空心圆之间有阴影。 在方括号和括号中，它的间隔表示法是负数 1 到 2。

    示例\(\PageIndex{12}\)

    解决复合不等式。 绘制解图并用区间表示法写出解:\(−3<2x−5\leq 1\).

    回答

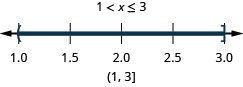
    解为 1 小于 x，即小于或等于 3。 它的图形在 1 处有一个空圆，在 3 处有一个封闭的圆，封闭圆和空心圆之间有阴影。 它的间隔符号在圆括号和括号内为负 1 到 3。

    用 “或” 求解复合不等式

    要用 “或” 求解复合不等式，我们一开始就用 “and” 求解复合不等式，我们求解这两个不等式。 然后我们找到所有使任一不等式都成真的数字。

    正如美国是所有50个州的联盟一样，解决方案将是将所有使不平等成为现实的数字合并。 为了找到复合不等式的解，我们查看每个不等式的图，找到属于任一图的数字，然后将所有这些数字放在一起。

    要用区间表示法写解，我们经常使用联合符\(\cup\)号来显示图中所示解的并集。

    用 “OR” 求解复合不等式。
    1. 解决每个不等式。
    2. 绘制每个解决方案的图表。 然后绘制使任一不等式都成真的数字的图表。
    3. 用间隔表示法写出解。
    示例\(\PageIndex{13}\)

    求解\(5−3x\leq −1\)或\(8+2x\leq 5\)。 绘制解图并用区间表示法写出解。

    回答
      \(5−3x\leq −1\) 要么 \(8+2x\leq 5\)
    解决每个不等式。 \(5−3x\leq −1\)   \(8+2x\leq 5\)
      \(−3x\leq −6\)   \(2x\leq −3\)
      \(x\geq 2\) 要么 \(x\leq −\frac{3}{2}\)
    绘制每个解决方案的图表。 。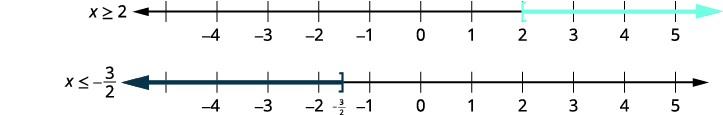

    使任一不等式都
    成真的图形数字。    		 。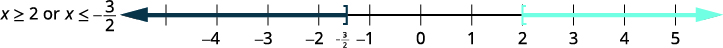
      \((−\infty,−32]\cup[2,\infty)\)
    示例\(\PageIndex{14}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(1−2x\leq −3\)或\(7+3x\leq 4\)。

    回答

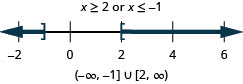
    解是 x 大于或等于 2 或 x 小于或等于 1。 数字线上的解图在负 1 处有一个封闭的圆圈，左边是阴影，2 处有一个封闭的圆圈，右边是阴影。 间隔表示法是圆括号和方括号内负无穷大与负 1 的并集，以及括号和括号内的 2 和无穷大的并集。

    示例\(\PageIndex{15}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(2−5x\leq −3\)或\(5+2x\leq 3\)。

    回答

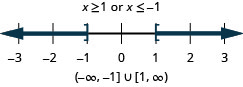
    解是 x 大于或等于 1 或 x 小于或等于负 1。 数字线上的解图在负 1 处有一个封闭的圆圈，左边是阴影，1 处有一个封闭的圆圈，右边是阴影。 间隔表示法是圆括号和方括号内负无穷大与负 1 的并集，以及括号和括号内的 1 和无穷大的并集。

    示例\(\PageIndex{16}\)

    求解\(\frac{2}{3}x−4\leq 3\)或\(\frac{1}{4}(x+8)\geq −1\)。 绘制解图并用区间表示法写出解。

    回答
      \(\frac{2}{3}x−4\leq 3\) 要么 \(\frac{1}{4}(x+8)\geq −1\)
    解决每个
    不等式。    		 \(3(\frac{2}{3}x−4)\leq 3(3)\)   \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\)
      \(2x−12\leq 9\)   \(x+8\geq −4\)
      \(2x\leq 21\)   \(x\geq −12\)
      \(x\leq \frac{21}{2}\)    
      \(x\leq \frac{21}{2}\) 要么 \(x\geq −12\)
    绘制每个
    解决方案的图表。    		 。
    使任一
    不等式都成真的图形数字
    。    		 。
      该解决方案涵盖所有实数。
      \((−\infty ,\infty )\)
    示例\(\PageIndex{17}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(\frac{3}{5}x−7\leq −1\)或\(\frac{1}{3}(x+6)\geq −2\)。

    回答

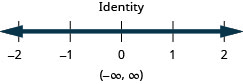
    解决方案是身份。 它在数字线上的解为所有值的阴影。 区间表示法中的解是圆括号内的负无穷大到无穷大。

    示例\(\PageIndex{18}\)

    解决复合不等式。 绘制解图并用区间表示法写出解：\(\frac{3}{4}x−3\leq 3\)或\(\frac{2}{5}(x+10)\geq 0\)。

    回答

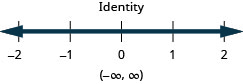
    解决方案是身份。 它在数字线上的解为所有值的阴影。 区间表示法中的解是圆括号内的负无穷大到无穷大。

    使用复合不等式求解应用程序

    现实世界中的情况还涉及复合不平等。 我们将使用与求解线性方程和不等式应用程序相同的问题求解策略。

    回想一下，解决问题的策略是首先阅读问题并确保所有单词都被理解。 然后，确定我们要查找的内容并分配一个变量来表示它。 接下来，用一句话重述问题，以便于将其转化为复合不等式。 最后，我们将解决复合不平等问题。

    示例\(\PageIndex{19}\)

    由于加利福尼亚的干旱，许多社区实行了分级水费。 “保护使用”、“正常使用” 和 “过度使用” 有不同的费率。 使用量以业主使用的百立方英尺（hcf）数来衡量。

    夏季，业主将支付24.72美元，外加每hcf1.54美元的普通使用费。 普通使用的账单将在或等于57.06美元和171.02美元之间。 如果所有者想让自己的使用量保持在正常范围内，他能使用多少 hcf？

    回答
    确定我们在寻找什么。 他可以使用的HCF数量并保持在 “正常使用” 计费范围内。
    说出我们要找的东西。 假设 x=x= 他能使用的 hcf 的数量。
    转化为不平等。 账单是24.72美元，再加上他使用的hcf数量的1.54倍或\(24.72+1.54x\)。
     

    \(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\)

    \(57.06 \leq 24.74 + 1.54x \leq 171.02 \)
    解决不平等问题。

    \(57.06 \leq 24.74 + 1.54x \leq 171.02\)

    \(57.06 \,{\color{red}{- \,24.72}}\leq 24.74 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\)

    \( 32.34 \leq 1.54x \leq 146.3\)

    \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\)

    \( 21 \leq x \leq 95 \)
    回答问题。 业主可以使用\(21–95\) hcf，但仍在 “正常使用” 计费范围内。
    示例\(\PageIndex{20}\)

    由于加利福尼亚的干旱，许多社区现在实行了分级水费。 “保护使用”、“正常使用” 和 “过度使用” 有不同的费率。 使用量以业主使用的百立方英尺（hcf）数来衡量。

    夏季，业主将支付24.72美元，外加每hcf1.32美元用于保护用途。 保护用途的账单将在或等于31.32美元和52.12美元之间。 如果主人想让自己的使用量保持在保护区内，她能使用多少 hcf？

    回答

    房主可以使用\(5–20\) hcf，但仍在 “保护用途” 计费范围内。

    示例\(\PageIndex{21}\)

    由于加利福尼亚的干旱，许多社区实行了分级水费。 “保护使用”、“正常使用” 和 “过度使用” 有不同的费率。 使用量以业主使用的百立方英尺（hcf）数来衡量。

    在冬季，业主将支付24.72美元，外加每hcf1.54美元的普通使用费。 普通使用的账单将在或等于49.36美元和86.32美元之间。 如果他想让自己的使用量保持在正常范围内，他将被允许使用多少 hcf？

    回答

    房主可以使用\(16–40\) hcf，但仍在 “正常使用” 计费范围内。

    访问此在线资源，获取有关解决复合不等式的更多指导和练习。

    • 复合不等式

    关键概念

    • 如何用 “and” 求解复合不等式
      1. 解决每个不等式。
      2. 绘制每个解决方案的图表。 然后绘制使两个不等式都成真的数字的图形。 这张图显示了复合不等式的解。
      3. 用间隔表示法写出解。
    • 双重不等式
      • 双重不等式是一种复合不等式，例如\(a<x<b\)。 它等同于\(a<x\)\(x<b.\)

        和其他形式：\ [\ begin {align*} a<x<b &\ text {等同于} & a<x\;\ text {和}\; x<b\\
        a≤b &\ text {等同于} & a≤x\;\ text {和}\; x≤b\\
        a>x>b &\ text {等同于} & a>x\;\ text {和}\; x>b\\
        a≥x≥b &\ text {等同于} & a≥x\;\ text {和}\; x≥b\ end {align*}\]
    • 如何用 “或” 求解复合不等式
      1. 解决每个不等式。
      2. 绘制每个解决方案的图表。 然后绘制使任一不等式都成真的数字的图表。
      3. 用间隔表示法写出解。

    词汇表

    复合不等式
    复合不等式由两个由单词 “and” 或 “or” 相连的不等式组成。