2.6E：练习

练习成就完美

在数字线上绘制不等式图

在以下练习中，在数字行上绘制每个不等式的图形，然后用间隔符号书写。

1. ⓐ\(x<−2\)
ⓑ\(x\geq −3.5\)
ⓒ\(x\leq \frac{2}{3}\)

2. ⓐ\(x>3\)
ⓑ\(x\leq −0.5\)
ⓒ\(x\geq \frac{1}{3}\)

回答

ⓐ

ⓑ

ⓒ

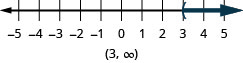
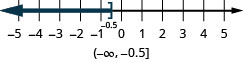
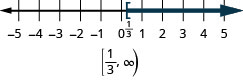
3. ⓐ\(x\geq −4\)
ⓑ\(x<2.5\)
ⓒ\(x>−\frac{3}{2}\)

4. ⓐ\(x\leq 5\)
ⓑ\(x\geq −1.5\)
ⓒ\(x<−\frac{7}{3}\)

回答

ⓐ

ⓑ

ⓒ

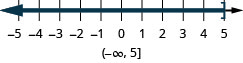
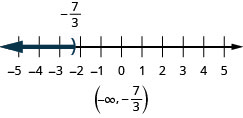
5. ⓐ\(−5<x<2\)
ⓑ\(−3\leq x<−1\)
ⓒ\(0\leq x\leq 1.5\)

6. ⓐ\(−2<x<0\)
ⓑ\(−5\leq x<−3\)
ⓒ\(0\leq x\leq 3.5\)

回答

ⓐ

ⓑ

ⓒ

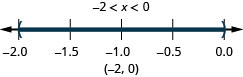
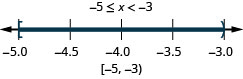
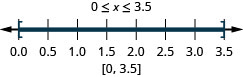
7. ⓐ\(−1<x<3\)
ⓑ\(−3<x\leq −2\)
ⓒ\(−1.25\leq x\leq 0\)

8. ⓐ\(−4<x<2\)
ⓑ\(−5<x\leq −2\)
ⓒ\(−3.75\leq x\leq 0\)

回答

ⓐ

ⓑ

ⓒ

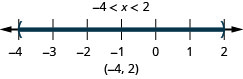
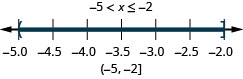
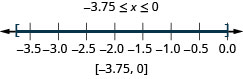
求解线性不等式

在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

9. ⓐ\(a+\frac{3}{4}\geq \frac{7}{10}\)
ⓑ\(8x>72\)
ⓒ\(20>\frac{2}{5}h\)

10. ⓐ\(b+\frac{7}{8}\geq \frac{1}{6}\)
ⓑ\(6y<48\)
ⓒ\(40<\frac{5}{8}k\)

回答

ⓐ

ⓑ

ⓒ

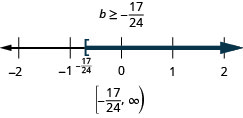
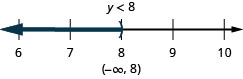
11. ⓐ\(f−\frac{13}{20}<−\frac{5}{12}\)
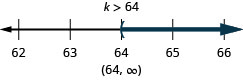
ⓑ\(9t\geq −27\)
ⓒ\(\frac{7}{6}j\geq 42\)

12. ⓐ\(g−\frac{11}{12}<−\frac{5}{18}\)
ⓑ\(7s<−28\)
ⓒ\(\frac{9}{4}g\leq 36\)

回答

ⓐ

ⓑ

ⓒ

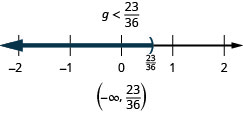
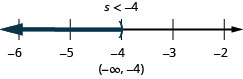
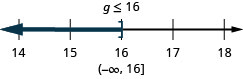
13. ⓐ\(−5u\geq 65\)
ⓑ\(\frac{a}{−3}\leq 9\)

14. ⓐ\(−8v\leq 96\)
ⓑ\(\frac{b}{−10}\geq 30\)

回答

ⓐ

ⓑ

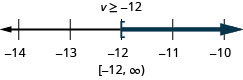
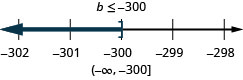
15. ⓐ\(−9c<126\)
ⓑ\(−25<\frac{p}{−5}\)

16. ⓐ\(−7d>105\)
ⓑ\(−18>\frac{q}{−6}\)

回答

ⓐ

ⓑ

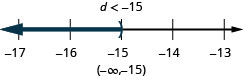
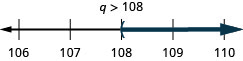
在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

17。 \(4v\geq 9v−40\)

18。 \(5u\leq 8u−21\)

回答

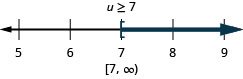
19。 \(13q<7q−29\)

20。 \(9p>14p−18\)

回答

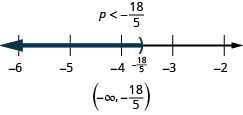
21。 \(12x+3(x+7)>10x−24\)

22。 \(9y+5(y+3)<4y−35\)

回答

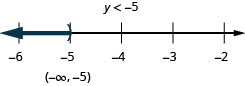
23。 \(6h−4(h−1)\leq 7h−11\)

24。 \(4k−(k−2)\geq 7k−26\)

回答

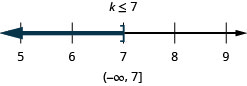
25。 \(8m−2(14−m)\geq 7(m−4)+3m\)

26。 \(6n−12(3−n)\leq 9(n−4)+9n\)

回答

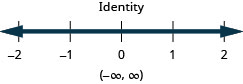
27。 \(\frac{3}{4}b−\frac{1}{3}b<\frac{5}{12}b−\frac{1}{2}\)

28。 \(9u+5(2u−5)\geq 12(u−1)+7u\)

回答

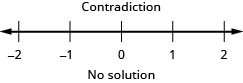
29。 \(\frac{2}{3}g−\frac{1}{2}(g−14)\leq \frac{1}{6}(g+42)\)

30。 \(\frac{4}{5}h−\frac{2}{3}(h−9)\geq \frac{1}{15}(2h+90)\)

回答

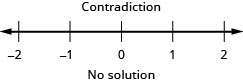
31。 \(\frac{5}{6}a−\frac{1}{4}a>\frac{7}{12}a+\frac{2}{3}\)

32。 \(12v+3(4v−1)\leq 19(v−2)+5v\)

回答

在以下练习中，求解每个不等式，在数字线上绘制解图，然后用区间表示法写出解。

33。 \(15k\leq −40\)

34。 \(35k\geq −77\)

回答

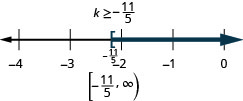
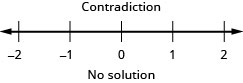
35。 \(23p−2(6−5p)>3(11p−4)\)

36。 \(18q−4(10−3q)<5(6q−8)\)

回答

37。 \(−\frac{9}{4}x\geq −\frac{5}{12}\)

38。 \(−\frac{21}{8}y\leq −\frac{15}{28}\)

回答

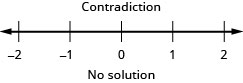
39。 \(c+34<−99\)

40。 \(d+29>−61\)

回答

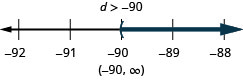
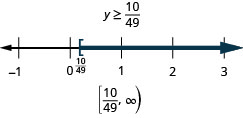
41。 \(\frac{m}{18}\geq −4\)

42。 \(\frac{n}{13}\leq −6\)

回答

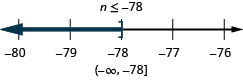
转化为不等式并求解

在以下练习中，翻译并求解。 然后在数字行上绘制解图，并用区间表示法写出解。

43。 三多\(h\)于不少于\(25\)。

44。 \(k\)超过六个\(25\)。

回答

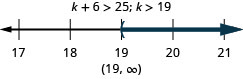
45。 少\(w\)于至少十个\(39\)。

46。 小于十二等\(x\)于不小于\(21\)。

回答

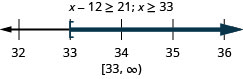
47。 负五倍\(r\)不超过\(95\)。

48。 负两倍低\(s\)于\(56\)。

回答

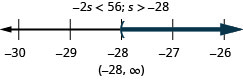
49。 最多比\(b\)现在少十九\(−22\)。

50。 至少\(a\)少十五\(−7\)。

回答

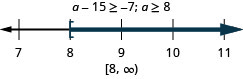
求解具有线性不等式的应用程序

在以下练习中，求解。

51。 艾伦正在装一个托盘，里面装有每个重达 45 磅的箱子。 托盘可以安全地承受不超过 900 磅的重量。 他可以安全地将多少箱子装到托盘上？

52。 Yehire 公寓楼的电梯有一个标志，上面写着最大重量为 2100 磅。 如果一个人的平均体重为 150 磅，那么有多少人可以安全地乘坐电梯？

回答

最多 14 人可以安全地乘坐电梯。

53。 安德烈正在和他的三个朋友一起看公寓。 他们希望月租金不超过2,360美元。 如果室友将租金平均分配给四人，那么每人支付的最高租金是多少？

54。 阿琳得到了一张20美元的咖啡店礼品卡。 她最喜欢的冰饮价格为3.79美元。 她可以使用礼品卡购买的最大饮料数量是多少？

回答

五杯饮料

55。 Teegan 喜欢打高尔夫球。 他下个月的练习场预算为60美元。 他每次去买一桶球要花10.55美元。 下个月他能去练习场的最大次数是多少？

56。 瑞安向邻居收取17.50美元的洗车费。 如果他的目标是赚到至少1,500美元，明年夏天他必须洗多少辆车？

回答

86 辆汽车

57。 Keshad 每月获得 2,400 美元的报酬，外加 6% 的销售额。 他的兄弟每月的收入为3,300美元。 Keshad的月薪会比他兄弟的月薪高出多少总销售额？

58。 Kimuyen 每月需要赚取 4,150 美元才能支付所有费用。 她的工作每月为她支付3,475美元，外加总销售额的4％。 为了支付所有费用，Kimuyen 的最低总销售额必须是多少？

回答

16,875 美元

59。 安德烈获得了一份入门级工作。 该公司每年向他提供48,000美元，外加他总销售额的3.5％。 安德烈知道这份工作的平均工资为62,000美元。 安德烈的总销售额需要多少，他的薪水才能至少与这份工作的平均工资一样高？

60。 娜塔莉正在考虑两份工作机会。 第一份工作每年将向她支付83,000美元。 第二个将向她支付66,500美元，再加上她总销售额的15％。 要使第二个报价的薪水高于第一个报价，她的总销售额需要多少？

回答

110,000 美元

61。 杰克的水费为每月24.80美元，外加每立方英尺（百立方英尺）水2.20美元。 如果Jake希望账单不超过60美元，他最多可以使用多少ccf？

62。 Kiyoshi的电话套餐费用为每月17.50美元，外加每条短信0.15美元。 Kiyoshi 可以使用的最大短信数量是多少，因此电话账单不超过 56.60 美元？

回答

260 条消息

63。 马龙的电视套餐每月收费49.99美元，另加每部首映电影5.49美元。 如果他想将每月账单保持在100美元的最高水平，他能看多少部首映电影？

64。 凯伦想在餐厅租一间宴会厅给她堂兄的婴儿洗澡。 餐厅的宴会厅收费350美元，午餐费用为每人32.50美元。 如果凯伦希望最高费用为1,500美元，她能有多少人去洗澡？

回答

35 个人

65。 Moshde 在她家经营一家发型设计公司。 她为发型和造型收取45美元的费用。 她每月的开支是960美元。 她希望每月能够在储蓄账户中存入至少1200美元，以开设自己的沙龙。 她必须做多少 “剪裁和款式” 才能每月至少节省 1200 美元？

66。 Noe 在家用计算机上安装和配置软件。 他每份工作收取125美元的费用。 他每月的开支为1,600美元。 他必须工作多少工作才能获得至少2400美元的利润？

回答

32 个职位

67。 凯瑟琳是一名私人厨师。 她每顿四人餐收费115美元。 她每月的开支是3,150美元。 她必须卖多少四人餐才能赚取至少1900美元的利润？

68。 Melissa 制作项链并在网上销售。 她每条项链收费88美元。 她每月的开支为3,745美元。 如果她想赚取至少1,650美元的利润，她必须卖多少项链？

回答

62 条项链

69。 五名学生会官员想参加州会议。 注册费用为110美元，交通和食物费用为375美元，酒店每人42美元。 学生会储蓄账户中有450美元的会议预算。 他们可以通过洗车来赚取所需的其余钱。 如果他们每辆车收取5美元，那么他们必须洗多少辆车才能有足够的钱支付旅行费用？

70。 塞萨尔正计划进行为期四天的旅行，去另一个州的一所大学探望他的朋友。 这将花费他198美元的机票，56美元的当地交通费用，每天45美元的食物费用。 他有189美元的储蓄，每修一片草坪可以赚35美元。 他必须修剪多少草坪才能有足够的钱支付旅行费用？

回答

七个草坪

71。 阿隆佐是一名汽车细节设计师。 他每辆车收费175美元。 他正计划搬出父母的房子，租用他的第一套公寓。 他需要支付120美元的申请费，950美元的保证金，以及第一个月和最后一个月的租金，每月1,140美元。 他有1,810美元的储蓄。 他必须详细说明多少辆车才能有足够的钱租公寓？

72。 Eun-Kyung 是一名导师，每小时的收入为 60 美元。 她有792美元的储蓄。 她正计划为父母举行周年派对。 她想邀请 40 位客人。 派对将花费她1,520美元购买食物和饮料，150美元购买摄影师。 她还将为每位客人提供一个礼物，每份礼物的费用为7.50美元。 她必须辅导多少小时才能有足够的钱参加聚会？

回答

20 个小时

日常数学

73。 舞台上的最大负荷 2014年，加利福尼亚州富乐顿的一个高中舞台倒塌了，当时有250名学生登上舞台观看音乐剧的结局。 二十多名学生受伤。 该舞台最多可支撑12,750磅。 如果假设学生的平均体重为140磅，那么最多可以安全上台的学生人数是多少？

74。 船上的最大重量 2004 年，一辆水上出租车在巴尔的摩港沉没，五人溺水身亡。 水上出租车的最大容量为 3,500 磅（25 人，平均体重 140 磅）。 水上出租车沉没时乘坐25人的平均体重为每人168磅。 这种体重的最大人数应该是多少？

回答

20 个人

75。 婚礼预算阿黛尔和沃尔特为他们的婚宴找到了理想的场地。 最多100位客人的费用为9850美元，每增加一位客人的费用为38美元。 如果阿黛尔和沃尔特希望总费用不超过12,500美元，可以有多少客人参加？

76。 淋浴预算 Penny 正计划为她的 daughter 妇洗个澡。 餐厅最多可容纳 25 位客人 950 美元，每增加一位客人 31.95 美元。 如果 Penny 希望总费用不超过 1,500 美元，可以有多少房客参加？

回答

42 位客人

写作练习

77。 解释为什么在求解时必须扭转不等式\(−5x>10\)。

78。 解释为什么在求解时必须扭转不等式\(n−3<12\)。

回答

答案会有所不同。

79。 查找你上个月的电话账单和你在工作中获得的小时工资。 通过写出适当的不等式然后解决这个问题，计算你赚到至少足够的钱来支付电话账单所花费的工作时数。 你觉得这个小时数合适吗？ 这是适合您的电话套餐吗？

80。 找出这个学期结束后你还剩下多少单元来实现你的大学目标，并估算你在大学里每学期可以学习的单元数量。 通过写一个适当的不等式然后解决这个问题来计算你实现大学目标所需的学期数。 在你实现目标之前，这是可接受的术语数量吗？ 有哪些方法可以加快这个过程？

回答

答案会有所不同。

自检

ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。

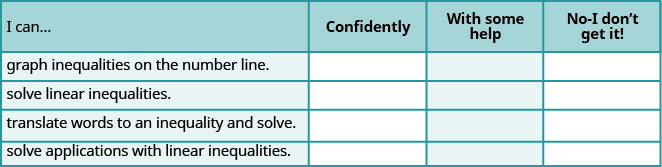
ⓑ 看完清单后，你认为你为下一节做好了充分的准备吗？ 为什么或者为什么不呢？