2.6: 求解线性不等式
- Page ID
- 204242
在本节结束时,您将能够:
- 在数字线上绘制不等式图
- 求解线性不等式
- 将单词翻译成不等式并求解
- 求解具有线性不等式的应用程序
在开始之前,请参加这个准备测验。
在数字线上绘制不等式图
什么数字能使不平等成为\(x>3\)现实? 你在想 “\(x\)可能是四个” 吗? 没错,但也\(x\)可能是 6 或 37,甚至是 3.001。 任何大于三的数字都是不等式的解\(x>3\)。 我们通过在三个右边的所有数字\(x>3\)上加阴影来显示数字线上不等式的所有解,以表明所有大于三的数字都是解。 因为数字三本身不是解,所以我们在三处加了一个左括号。
我们也可以使用区间表示法表示不等式。 这种不平等的解决方案没有上限。 在间隔表示法中,我们表示\(x>3\)为\((3,\infty)\)。 该符号\(\infty\)被读为 “无限”。 这不是一个实际的数字。 图中同时\(\PageIndex{1}\)显示了数字线和间隔符号。
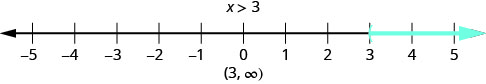
我们使用左括号符号 (, 来表示不等式的端点不包括在内。 左方括号符号 [表示包含端点。
不等\(x\leq 1\)式意味着所有数字小于或等于一。 在这里,我们需要证明一个也是一种解决方案。 我们通过在方括号上加上方括号来做到这一点\(x=1\)。 然后,我们将一个左边的所有数字加上阴影,以表明所有小于一的数字都是解(图\(\PageIndex{2}\))。 这些数字没有下限。 我们用间隔表示法写\(x\leq 1x\leq 1 \)成\((−\infty,1]\)。 该符号\(−\infty\)被读为 “负无穷大”。
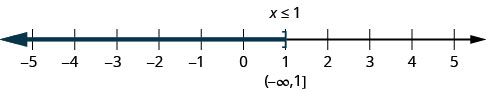
图中同时\(\PageIndex{3}\)显示了数字行和间隔符号。

数字线和区间表示法中的不等式表示法使用相同的符号来表示间隔的端点。
在数字行上绘制每个不等式的图形,并用间隔符号书写。
- \(x\geq −3\)
- \(x<2.5\)
- \(x\leq −\frac{3}{5}\)
- 回答
-
ⓐ
\( x \geq -3 \) 向右移动\(−3\),然后在上面放一个括号\(−3\)。 
用间隔符号书写。 \( [-3, \infty) \) ⓑ
\( x < 2.5 \) 在 2.5 的左侧加上阴影,然后在 2.5 处加上括号。 
用间隔符号书写。 \( (-\infty, 2.5) \) ⓒ
\( x \leq -\dfrac{3}{5} \) 向左移动\(−\frac{3}{5}\),然后在上面放一个括号\(−\frac{3}{5}\)。 
用间隔符号书写。 \( \bigg( -\infty, \dfrac{3}{5}\bigg] \)
在数字行上绘制每个不等式的图形,并用间隔符号书写:
- \(x>2\)
- \(x\leq −1.5\)
- \(x\geq \frac{3}{4}\)。
- 回答
-
ⓐ
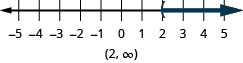
ⓑ
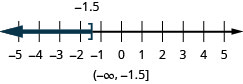
ⓒ
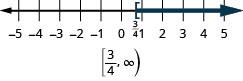
在数字行上绘制每个不等式的图形,并用间隔符号书写:
- \(x\leq −4\)
- \(x\geq 0.5\)
- \(x<−\frac{2}{3}\)。
- 回答
-
ⓐ
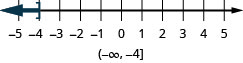
ⓑ

ⓒ
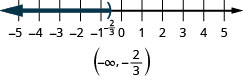
哪些数字大于二但小于五? 你在想说\(2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99\)吗,? 我们可以用不等式来表示二到五之间的所有数字\(2<x<5\)。 我们可以通过将二到五之间的所有数字加\(2<x<5\)上阴影来显示在数字行上。 同样,我们使用圆括号来表示数字二和五不包括在内。 参见图。

在数字行上绘制每个不等式的图形,并用间隔符号书写。
ⓐ\(−3<x<4\) ⓑ\(−6\leq x<−1\) ⓒ\(0\leq x\leq 2.5\)
- 回答
-
ⓐ
\(-3 < x < 4\) 介于\(−3\)和 4 之间的阴影。
在\(−3\)和 4 处加上圆括号。
用间隔符号书写。 \( (-3,4) \) ⓑ
\( -6 \leq x < -1 \) 介于\(−6\)和 −1 之间的阴影。
在 −1 处加上方括号\(−6\)
,在 −1 处加上圆括号。
用间隔符号书写。 \( [-6,1) \) ⓒ
\( 0 \leq x \leq 2.5 \) 阴影介于 0 和 2.5 之间。
在 0 和 2.5 处放置一个括号。
用间隔符号书写。 \( [0, 2.5] \)
在数字行上绘制每个不等式的图形,并用间隔符号书写:
ⓐ\(−2<x<1\) ⓑ\(−5\leq x<−4\) ⓒ\(1\leq x\leq 4.25\)
- 回答
-
ⓐ
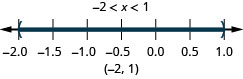
ⓑ
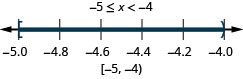
ⓒ
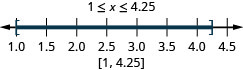
在数字行上绘制每个不等式的图形,并用间隔符号书写:
ⓐ\(−6<x<2\) ⓑ\(−3\leq x< −1\) ⓒ\(2.5\leq x\leq 6\)
- 回答
-
ⓐ
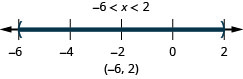
ⓑ
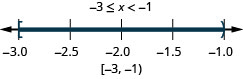
ⓒ
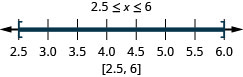
求解线性不等式
线性不等式很像线性方程,但等号被不等号所取代。 线性不等式是一个变量中的不等式,可以用、\(ax+b<c\)\(ax+b\leq c\)\(ax+b>c\)、或的形式写成\(ax+b\geq c\)。
线性不等式是一个变量中的不等式,可以用以下形式之一书写,其中\(a, \, b,\)和\(c\)是实数,并且\(a≠0\):
\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]
当我们求解线性方程时,我们能够使用相等的属性将两边相加、减去、乘或除,同时仍然保持相等。 对于不等式,类似的属性也适用。
我们可以从不等式的两边加上或减去相同的数量,但仍然保持不等式。 例如:
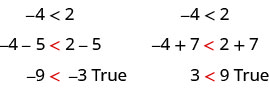
请注意,不等式符号保持不变。
这使我们想到了不等式的加减属性。
对于任何数字\(a, \, b,\)和 i\(c,\) f\(a<b\),那么
\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]
我们可以从不等式的两边加上或减去相同的数量,但仍然保持不等式
当我们将两边除以或乘以一个常数时,不等式会发生什么?
让我们先将两边乘以一个正数。
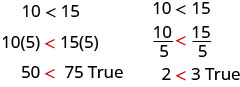
不平等迹象保持不变。
当我们除以或乘以负数时,不等式是否保持不变?
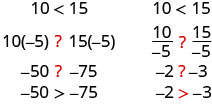
请注意,当我们填写不等式符号时,不平等标志的方向发生了逆转。
当我们将不等式除以或乘以正数时,不等式符号保持不变。 当我们将不等式除以或乘以负数时,不等式符号反转。
这为我们提供了不等式的乘法和除法属性。
对于任何数字\(a, \, b,\)和\(c,\)
\[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]
当我们将不等式除以或乘以时\(a\):
- 正数,不等式保持不变。
- 负数,不等式反转。
有时在求解不等式时,如下一个示例所示,变量在右边结束。 我们可以反向重写不等式,将变量放在左边。
\[x>a \text{ has the same meaning as } a<x \nonumber \]
可以把它当作 “如果 Xander 比 Andy 高,那么 Andy 比 Xander 短。”
解决每个不等式。 在数字行上绘制解图,然后用区间表示法写出解。
ⓐ\(x−\frac{3}{8}\leq \frac{3}{4}\) ⓑ\(9y<54\) ⓒ\(−15<\frac{3}{5}z\)
- 回答
-
ⓐ
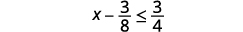
将不等式的两边加上 3838。 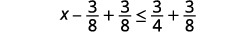
简化。 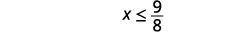
在数字行上绘制解法。 
用间隔表示法写出解。 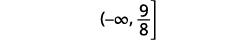
ⓑ
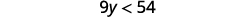
将不等式的两边除以 9;由于
9 为正,因此不等式保持不变。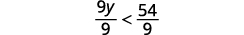
简化。 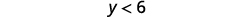
在数字行上绘制解法。 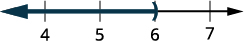
用间隔表示法写出解。 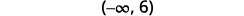
ⓒ
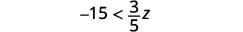
将不等式的两边乘以\(\frac{5}{3}\)。
因为\(\frac{5}{3}\)是正数,所以不等式保持不变。
简化。 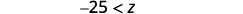
用左边的变量重写。 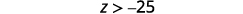
在数字行上绘制解法。 
用间隔表示法写出解。 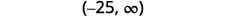
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解:
ⓐ\(p−\frac{3}{4}\geq \frac{1}{6}\) ⓑ\(9c>72\) ⓒ\(24\leq \frac{3}{8}m\)
- 回答
-
ⓐ
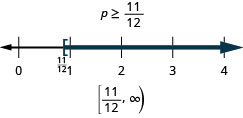
ⓑ
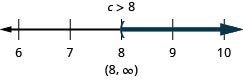
ⓒ
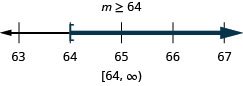
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解:
ⓐ\(r−\frac{1}{3}\leq \frac{7}{12}\) ⓑ\(12d\leq 60\) ⓒ\(−24<\frac{4}{3}n\)
- 回答
-
ⓐ
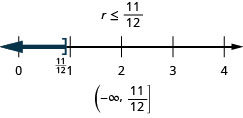
ⓑ
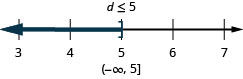
ⓒ
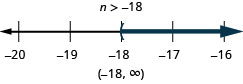
乘以或除以负数时要小心,记得反转不等式符号。
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解。
ⓐ\(−\frac{1}{3}m\geq \frac{6}{5}\) ⓑ\(\frac{n}{−2} \geq 8\)
- 回答
-
ⓐ
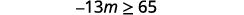
将不平等的两面除以\(−\frac{1}{3}\)。
既然\(−\frac{1}{3}\)是负数,不等式就会逆转。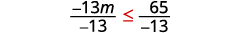
简化。 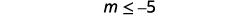
在数字行上绘制解法。 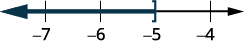
用间隔表示法写出解。 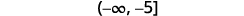
ⓑ
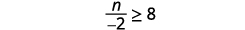
将不等式的两边乘以\(−2\)。
既然\(−2\)是负数,不等式就会逆转。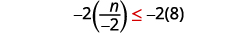
简化。 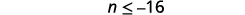
在数字行上绘制解法。 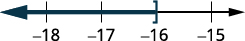
用间隔表示法写出解。 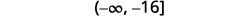
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解:
ⓐ\(−8q<32\) ⓑ\(\frac{k}{−12} \leq 15\)。
- 回答
-
ⓐ
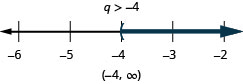
ⓑ
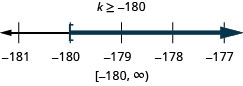
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解:
ⓐ\(−7r\leq −70\) ⓑ\(\frac{u}{−4}\geq −16\)。
- 回答
-
ⓐ
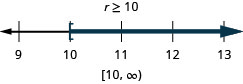
ⓑ
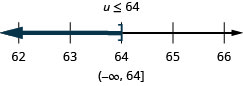
大多数不平等需要不止一个步骤才能解决。 我们遵循在求解线性方程的通用策略中使用的相同步骤,但是在乘法或除法以分离变量时,请务必密切注意。
求解不\(6y\leq 11y+17\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
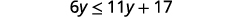
从两边减去 11y11y 以收集左边
的变量。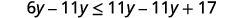
简化。 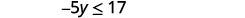
将不等式的两边除以 −5、−5,
然后反转不等式。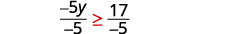
简化。 
在数字行上绘制解法。 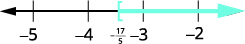
用间隔表示法写出解。 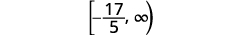
求解不等式,在数字线上绘出解,然后用区间表示法写出解:\(3q\geq 7q−23\)。
- 回答
-
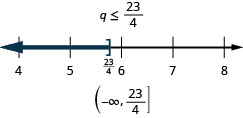
求解不等式,在数字线上绘出解,然后用区间表示法写出解:\(6x<10x+19\)。
- 回答
-
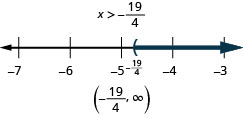
求解不等式时,通常最容易收集变量系数最大的一侧的变量。 这消除了负系数,因此我们不必乘以或除以负数,这意味着我们不必记得反转不等式符号。
求解不\(8p+3(p−12)>7p−28\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
\(8p+3(p−12)>7p−28\) 尽可能简化每一面。 分发。 \(8p+3p−36>7p−28\) 将相似的术语组合在一起。 \(11p−36>7p−28\) \(7p\)从两边减去以收集左边的
变量,因为\(11>7\)。\(11p−36−7p>7p−28−7p\) 简化。 \(4p−36>−28\) \(36\)向两边添加以收集右侧的
常量。\(4p−36+36>−28+36\) 简化。 \(4p>8\) 将不等式的两边除以
\(4\);不等式保持不变。\(\dfrac{4p}{4}>\dfrac{8}{4}\) 简化。 \(p>2\) 在数字行上绘制解法。 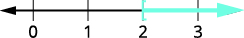
用间隔表示法写出解。 \((2,\infty)\)
求解不\(9y+2(y+6)>5y−24\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
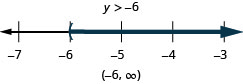
求解不\(6u+8(u−1)>10u+32\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
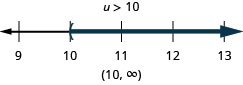
就像有些方程是身份而有些是矛盾一样,不平等也可能是身份或矛盾。 当我们在解决不等式时只剩下常量时,我们就会认出这些形式。 如果结果是真实的陈述,那么我们就有了身份。 如果结果是虚假陈述,那么我们就有矛盾了。
求解不\(8x−2(5−x)<4(x+9)+6x\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
尽可能简化每一面。 \(8x−2(5−x)<4(x+9)+6x\) 分发。 \(8x−10+2x<4x+36+6x\) 将相似的术语组合在一起。 \(10x−10<10x+36\) \({\color{red}{10x}}\)从两边减去以收集左边的变量。 \(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\) 简化。 \(−10<36\) 这些都消失了,我们有了一个真实的
陈述。\(x\)不平等是一种身份。
解决方案都是实数。在数字行上绘制解法。 
用间隔表示法写出解。 \((−\infty,\infty)\)
求解不\(4b−3(3−b)>5(b−6)+2b\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
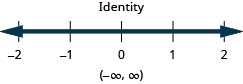
求解不\(9h−7(2−h)<8(h+11)+8h\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
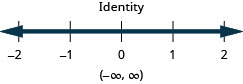
我们可以像在方程中一样清除不等式中的分数。 再说一遍,乘以或除以负数时要小心符号。
求解不\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\) 将两边乘以液晶屏 24
以清除分数。\({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\) 简化。 \( 8a - 3a > 5a + 18 \) 将相似的术语组合在一起。 \( 5a > 5a + 18\) \(5a\)从两边减去以收集左边的
变量。\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\) 简化。 \(0 > 18 \) 这个说法是错误的。 不平等是矛盾的。
没有解决办法。在数字行上绘制解法。 
用间隔表示法写出解。 没有解决办法。
求解不\(\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
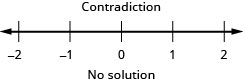
求解不\(\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
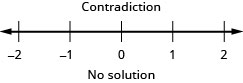
转化为不等式并求解
要将英语句子翻译成不等式,我们需要识别表示不平等的短语。 有些词很简单,比如 “大于” 和 “小于”。 但是其他的并不那么明显。 该@@ 表显示了一些表示不平等的常用短语。
| \(>\) | \(\geq\) | \(<\) | \(\leq\) |
|---|---|---|---|
| \ (>\) “>\)” data-valign= “middle” class= “lt-math-17389” > 大 于大于大 于大于 超过 |
\ (\ geq\)” data-valign= “middle” >大于或等 于至少不小 于最小值 |
\ 小于<\)” data-valign="middle"> 小于 小于小于 小于 小于 |
\ (\ leq\)” data-valign= “middle” >小于或等 于最多不大 于最大值 |
翻译并解决。 然后在数字行上绘制解图,并用区间表示法写出解。
\[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]
- 回答
-

翻译。 \(x - 27 \geq 48\) 求解-向两边加 27。 \( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\) 简化。 \(x \geq 75\) 数字线上的图形。 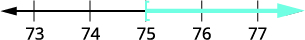
用间隔符号书写。 \([75, \infty)\)
翻译并解决。 然后在数字行上绘制解图,并用区间表示法写出解。
\[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]
- 回答
-
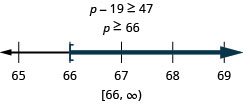
翻译并解决。 然后在数字行上绘制解图,并用区间表示法写出解。
\[\text{Four more than }a\text{ is at most }15.\nonumber\]
- 回答
-
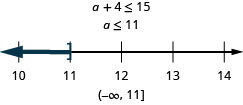
求解具有线性不等式的应用程序
许多现实生活中的情况要求我们解决不平等问题。 我们将用来求解具有线性不等式的应用程序的方法与我们在使用方程求解应用程序时使用的方法非常相似。
我们将阅读问题并确保所有单词都被理解。 接下来,我们将确定要查找的内容,并分配一个变量来表示它。 我们将用一句话重述这个问题,以便于将其转化为不平等。 然后,我们将解决不平等问题。
有时应用程序要求解为整数,但不等式的代数解不是整数。 在这种情况下,我们必须将代数解四舍五入到一个整数。 应用程序的上下文将决定我们是向上还是向下四舍五入。
黎明赢得了4,000美元的小额补助金,用于为她的教室购买平板电脑。 她想购买的平板电脑每台售价为254.12美元,包括税费和运费。 Dawn 可以购买的最大平板电脑数量是多少?
- 回答
-
\(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)
安吉有20美元可以花在果汁盒上,用于儿子的学前野餐。 每包果汁盒的价格为2.63美元。 她最多可以购买多少包?
- 回答
-
安吉可以买 7 包果汁。
丹尼尔想在她最喜欢的餐厅举办生日派对,给女友一个惊喜。 每人晚餐费用为42.75美元,包括小费和税费。 他的派对预算是500美元。 丹尼尔最多能参加派对的人数是多少?
- 回答
-
丹尼尔可以有 11 个人参加派对。
Taleisha的电话套餐每月花费28.80美元,外加每条短信0.20美元。 她可以发送/接收多少条短信,并且每月的电话账单不超过50美元?
- 回答
-
\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)
塞尔吉奥和利泽斯的度假预算非常紧张。 他们计划从一家公司租一辆汽车,每周收费75美元,外加每英里0.25美元。 他们在一周内可以行驶多少里程,但仍保持在 200 美元的预算范围内?
- 回答
-
塞尔吉奥和利泽斯的行驶里程不超过 500 英里。
Rameen的取暖费为每月5.42美元,加上每热1.08美元。 如果 Rameen 想让取暖费最高为 87.50 美元,他能使用多少保温器。
- 回答
-
Rameen的取暖费为每月5.42美元,加上每热1.08美元。 如果 Rameen 想让取暖费最高为 87.50 美元,他能使用多少保温器。
利润是指从收入中减去成本后剩余的钱。 在下一个例子中,我们将找到一个小女商人为了赚取一定利润每个月需要做的工作数量。
Felicity 有一家书法生意。 她每张结婚请柬收取2.50美元的费用。 她每月的开支是650美元。 她必须写多少邀请函才能赚取每月至少2,800美元的利润?
- 回答
-
\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)
Caleb 有一家宠物看护公司。 他每小时收费32美元。 他每月的开支为2,272美元。 他必须工作多少小时才能赚取每月至少800美元的利润?
- 回答
-
Caleb 必须工作至少 96 个小时。
艾略特经营景观维护业务。 他每月的开支为1,100美元。 如果他每份工作收取60美元,那么他必须做多少工作才能赚取每月至少4,000美元的利润?
- 回答
-
艾略特必须工作至少 85 个工作。
在许多情况下,多个数量会占总支出。 当我们解决这样的问题时,我们必须确保将所有个人开支考虑在内。
马利克正计划为期六天的暑假旅行。 他有840美元的储蓄,每小时的辅导收入为45美元。 这次旅行将花费他525美元的机票,780美元的食物和观光费用,每晚95美元的酒店费用。 他必须辅导多少小时才能有足够的钱支付旅行费用?
- 回答
-
\(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)
布伦达最好的朋友正在举行目的地婚礼,活动将持续三天。 布伦达有500美元的储蓄,每小时可以赚15美元的保姆服务。 她预计将支付350美元的机票,375美元的食物和娱乐费用以及每晚60美元的酒店房间份额。 她必须照顾多少小时才能有足够的钱支付旅行费用?
- 回答
-
布伦达必须照看至少 27 个小时。
Josue想在明年春天和朋友一起去10晚的公路旅行。 他将花费180美元购买汽油,450美元购买食物,每晚花费49美元。 他有520美元的储蓄,每条车道铲雪可以赚30美元。 他必须铲多少车道才能有足够的钱支付旅行费用?
- 回答
-
Josue 必须铲掉至少 20 条车道。
关键概念
- 不等式、数字线和间隔记法
\(x>a \quad x\geq a\quad x<a\quad x\leq a\)

- 线性不等式
- 线性不等式是一个变量中的不等式,可以用以下形式写成,其中 a、b 和 c 是实数,并且\(a\neq 0\):
\[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
- 线性不等式是一个变量中的不等式,可以用以下形式写成,其中 a、b 和 c 是实数,并且\(a\neq 0\):
- 不等式的加减特性
- 对于任何数字 a、b 和 c,如果 a<b,那么 na<b,那么
\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- 我们可以从不等式的两边加上或减去相同的数量,但仍然保持不等式。
- 对于任何数字 a、b 和 c,如果 a<b,那么 na<b,那么
- 不等式的乘法和除法特性
- 对于任何数字 a、b 和 c,
\(\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}\)
- 对于任何数字 a、b 和 c,
- 表示不平等的短语
\(>\) \(\geq\) \(<\) \(\leq\) \ (>\) “>大于大
于大
于大于
超过\ (\ geq\)” data-valign= “middle” >大于或等
于至少不小
于最小值
\ 小于<\)” data-valign="middle"> 小于
小于小于
小于
小于\ (\ leq\)” data-valign= “middle” >小于或等
于最多不大
于最大值


