2.7: أمثلة جبر المتجهات
- Page ID
- 199897
يتم تحديد ثلاثة متجهات للإزاحة\(\vec{A}\)\(\vec{B}\)،\(\vec{C}\) وفي المستوى (الشكل 2.3.6) بمقاييسها A = 10.0، B = 7.0، C = 8.0، على التوالي، ومن خلال زوايا الاتجاه الخاصة بكل منها مع الاتجاه الأفقي\(\alpha\) = 35 درجة،\(\beta\) = −110 درجة، و \(\gamma\)= 30 درجة. الوحدات المادية للمقاييس هي سنتيمترات. قم بحل المتجهات إلى مكوناتها العددية وابحث عن مجاميع المتجهات التالية:
- \(\vec{R}\)=\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\)،
- \(\vec{D}\)=\(\vec{A}\) −\(\vec{B}\)، و
- \(\vec{S}\)=\(\vec{A}\) − 3\(\vec{B}\) +\(\vec{C}\).
أولاً، نستخدم المعادلة 2.4.13 لإيجاد المكونات العددية لكل متجه ثم نعبر عن كل متجه في شكل مكون المتجه الخاص به المعطى بـ\(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}\). ثم نستخدم الطرق التحليلية للجبر المتجه للعثور على النتائج.
الحلنقوم بحل المتجهات المعطاة لمكوناتها العددية:
\[ \begin{cases} A_{x} = A \cos \alpha = (10.0\; cm) \cos {35^{o}} = 8.19\; cm \\ A_{y} = A \sin \alpha = (10.0\; cm) \sin{35^{o}} = 5.73\; cm \end{cases}\]
\[ \begin{cases} B_{x} = B \cos \beta = (7.0\; cm) \cos (-110^{o}) = -2.39\; cm \\ B_{y} = B \sin \beta= (7.0\; cm) \sin (-110^{o}) = -6.58\; cm \end{cases}\]
\[ \begin{cases} C_{x} = C \cos \gamma= (8.0\; cm) \cos (30^{o}) = 6.93\; cm \\ C_{y} = C \sin \gamma= (8.0\; cm) \sin(30^{o}) = 4.00\; cm \end{cases}\]
بالنسبة لـ (أ) قد نستبدل مباشرة بالمعادلة 2.6.7 للعثور على المكونات العددية للنتيجة:
\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = 8.19\; cm - 2.39\; cm + 6.93\; cm = 12.73\; cm \\ R_{y} = A_{y} + B_{y} + C_{y} = 5.73\; cm - 6.58\; cm + 4.00\; cm = 3.15\; cm \end{cases}\]
لذلك، يكون المتجه الناتج هو\(\vec{R} = R_{x} \hat{i} + R_{y} \hat{j} = (12.7 \hat{i} + 3.1 \hat{j})\) cm. بالنسبة إلى (b)، قد نرغب في كتابة فرق المتجهات على النحو التالي
\[\vec{D} = \vec{A} - \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j}) - (B_{x} \hat{i} + B_{y} \hat{j}) = (A_{x} - B_{x}) \hat{i} + (A_{y} - B_{y}) \hat{j} \ldotp\]
ومن ثم فإن متجه الفرق هو\(\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (10.6 \hat{i} + 12.3 \hat{j})\) سم.
بالنسبة لـ (c)، يمكننا كتابة المتجه\(\vec{S}\) بالشكل الصريح التالي:
\[ \vec{S} = \vec{A} - 3 \vec{B} + \vec{C} = (A_{x} \hat{i} + A_{y} \hat{j}) - 3(B_{x} \hat{i} + B_{y} \hat{j}) + (C_{x} \hat{i} + C_{y} \hat{j}) = (A_{x} - 3 B_{x} + C_{x}) \hat{i} + (A_{y} - 3 B_{y} + C_{y}) \hat{j} \ldotp\]
ثم المكونات العددية\(\vec{S}\) هي
\[ \begin{cases} S_{x} = A_{x} - 3B_{x} + C_{x} = 8.19\; cm - 3(-2.39\; cm) + 6.93\; cm = 22.29\; cm \\ S_{y} = A_{y} - 3B_{y} + C_{y} = 5.73\; cm -3(-6.58\; cm) + 4.00\; cm = 29.47\; cm \end{cases}\]
المتجه هو\(\vec{S} = S_{x} \hat{i} + S_{y} \hat{j} = (22.3 \hat{i} + 29.5 \hat{j})\) سم.
الدلالةبعد العثور على مكونات المتجهات، يمكننا توضيح المتجهات بالرسم البياني أو يمكننا حساب المقادير وزوايا الاتجاه، كما هو موضح في الشكل\(\PageIndex{1}\). يمكن مقارنة نتائج المقادير في (ب) و (ج) بنتائج نفس المشكلات التي تم الحصول عليها باستخدام الطريقة الرسومية، الموضحة في الشكل 2.3.7 والشكل 2.3.8. لاحظ أن الطريقة التحليلية تنتج نتائج دقيقة وأن دقتها لا تقتصر على دقة المسطرة أو المنقلة، كما كان الحال مع الطريقة الرسومية المستخدمة في المثال 2.3.2 للعثور على نفس النتيجة.
يتم تحديد ثلاثة متجهات للإزاحة\(\vec{A}\)\(\vec{B}\)، و\(\vec{F}\) (الشكل 2.3.6) بمقاييسها A = 10.00، B = 7.00، و F = 20.00، على التوالي، ومن خلال زوايا الاتجاه الخاصة بكل منها مع الاتجاه الأفقي\(\alpha\) = 35 درجة،\(\beta\) = −110 درجة، و\(\varphi\) = 110 °. الوحدات المادية للمقاييس هي سنتيمترات. استخدم الطريقة التحليلية لإيجاد المتجه\(\vec{F}\) =\(\vec{A}\) + 2\(\vec{B}\) −\(\vec{F}\). تحقق من أن G = 28.15 سم وذاك\(\theta_{G}\) = −68.65 درجة.
تلعب أربعة كلاب اسمها أسترو وبالتو وكليفورد ودوغ لعبة شد الحبل باستخدام لعبة (الشكل\(\PageIndex{2}\)). يسحب أسترو اللعبة في الاتجاه\(\alpha\) = 55 درجة جنوب الشرق، ويسحب بالتو في الاتجاه\(\beta\) = 60 درجة شرق الشمال، ويسحب كليفورد في الاتجاه\(\gamma\) = 55 درجة غرب الشمال. يسحب أسترو بقوة بـ 160.0 وحدة من القوة (N)، والتي نختصرها كـ A = 160.0 N. يسحب Balto بقوة أقوى من Astro بقوة مقدارها B = 200.0 N، ويسحب كليفورد بقوة مقدارها C = 140.0 N. عندما يسحب دوغ اللعبة بطريقة تجعل قوته توازن ناتج القوى الثلاث الأخرى، لا تتحرك اللعبة في أي اتجاه. ما حجم القوة وفي أي اتجاه يجب أن يسحب دوغ اللعبة حتى يحدث هذا؟
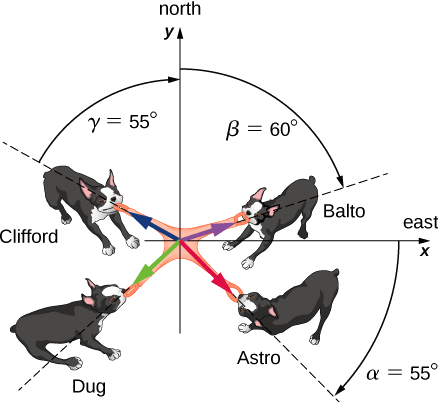
إستراتيجية
نفترض أن الشرق هو اتجاه المحور السيني الموجب والشمال هو اتجاه المحور y الموجب. كما هو الحال في المثال\(\PageIndex{1}\)، يتعين علينا حل القوى الثلاث المعطاة -\(\vec{A}\) (السحب من أسترو)،\(\vec{B}\) (السحب من بالتو)، و\(\vec{C}\) (السحب من كليفورد) - في مكوناتها العددية ثم العثور على المكونات العددية للمتجه الناتج\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) + \(\vec{C}\). عندما تقوم قوة السحب\(\vec{D}\) من Dug بموازنة هذا الناتج، يجب أن يعطي مجموع المتجه الفارغ\(\vec{D}\) +\(\vec{R}\) =\(\vec{D}\)\(\vec{R}\) ويجب أن يعطي ذلك المتجه الفارغ\(\vec{0}\). هذا يعني أن\(\vec{D}\) =\(- \vec{R}\) لذا يجب أن يكون السحب من Dog مضادًا لـ\(\vec{R}\).
الحل
زوايا الاتجاه هي\(\theta_{A}\)\(− \alpha\) = −55°،\(\theta_{B}\) = 90° −\(\beta\) = 30°، و\(\theta_{C}\) = 90° +\(\gamma\) = 145°، واستبدالها في المعادلة 2.4.13 يعطي المكونات العددية للقوى الثلاث المعطاة:
\[ \begin{cases} A_{x} = A \cos \theta_{A} = (160.0\; N) \cos (-55^{o}) = + 91.8\; N \\ A_{y} = A \sin \theta_{A} = (160.0\; N) \sin (-55^{o}) = -131.1\; N \end{cases}\]
\[ \begin{cases} B_{x} = B \cos \theta_{B} = (200.0\; N) \cos 30^{o} = + 173.2\; N \\ B_{y} = B \sin \theta_{B} = (200.0\; N) \sin 30^{o} = + 100.0\; N \end{cases}\]
\[ \begin{cases} C_{x} = C \cos \theta_{C} = (140.0\; N) \cos 145^{o} = -114.7\; N \\ C_{y} = C \sin \theta_{C} = (140.0\; N) \sin 145^{o} = + 80.3\; N \end{cases}\]
الآن نحسب المكونات العددية للمتجه الناتج\(\vec{R} = \vec{A} + \vec{B} + \vec{C}\):
\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = + 91.8\; N+ 173.2\; N- 114.7\; N = +150.3 \; N\\ R_{y} = A_{y} + B_{y} + C_{y} = -131.1\; N + 100.0\; N + 80.3\; N= +49.2\; N\end{cases}\]
المتجه المضاد للنتيجة\(\vec{R}\) هو
\[\vec{D} = -\vec{R} = -R_{x} \hat{i} - R_{y} \hat{j} = (-150.3 \hat{i} - 49.2 \hat{j}) N \ldotp\]
حجم قوة سحب دوغ هو
\[D = \sqrt{D_{x}^{2} + D_{y}^{2}} = \sqrt{(-150.3)^{2} + (-49.2)^{2}} N = 158.1\; N \ldotp\]
اتجاه قوة سحب دوغ هو
\[\theta = \tan^{-1} \left(\dfrac{D_{y}}{D_{x}}\right) = \tan^{-1} \left(\dfrac{-49.2\; N}{-150.3\; N}\right) = \tan^{-1} \left(\dfrac{49.2}{150.3}\right) = 18.1^{o}\ldotp\]
يتم السحب المحفور في اتجاه 18.1 درجة جنوب الغرب لأن كلا المكونين سالبين، مما يعني أن متجه السحب يقع في الربع الثالث (الشكل 2.4.4).
لنفترض أن Balto in Example\(\PageIndex{2}\) يغادر اللعبة ليهتم بأمور أكثر أهمية، لكن Astro و Clifford و Dug يواصلون اللعب. لا تتغير قوة سحب أسترو وكليفورد، لكن دوغ يركض ويعض اللعبة في مكان مختلف. ما مقدار القوة والاتجاه الذي يجب أن يسحبه دوغ في اللعبة الآن لموازنة عمليات السحب المجمعة من كليفورد وأسترو؟ قم بتوضيح هذا الموقف من خلال رسم مخطط متجه يشير إلى جميع القوى المعنية.
أوجد مقدار المتجه\(\vec{C}\) الذي يفي بالمعادلة ٢\(\vec{A}\) − ٦\(\vec{B}\) + ٣\(\vec{C}\) = ٢\(\hat{j}\)،\(\vec{A}\) =\(\hat{i}\) − ٢،\(\hat{k}\)\(\vec{B}\) و= −\(\hat{j}\) +\(\frac{\hat{k}}{2}\).
إستراتيجيةنحل أولاً المعادلة المعطاة للمتجه غير المعروف\(\vec{C}\). ثم نستبدل\(\vec{A}\)\(\vec{B}\) ونجمع المصطلحات على طول كل من الاتجاهات الثلاثة\(\hat{i}\)\(\hat{j}\)،\(\hat{k}\) ونحدد المكونات العددية C x و C y و C z. أخيرًا، نستبدل المعادلة 2.5.6 لإيجاد المقدار C.
الحل\[\begin{split} 2 \vec{A} - 6 \vec{B} +& 3 \vec{C} = 2 \hat{j}\\ & 3 \vec{C} = 2 \hat{j} - 2 \vec{A} + 6 \vec{B} \\ &\vec{C} = \frac{2}{3} \hat{j} - \frac{2}{3} \vec{A} + 2 \vec{B}\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} (\hat{i} - 2\hat{k}) + 2 \big(- \hat{j} + \frac{\hat{k}}{2}\big)\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} \hat{i} + \frac{4}{3} \hat{k} - 2 \hat{j} + \hat{k}\\ & \quad = -\frac{2}{3} \hat{i} + \big(\frac{2}{3} - 2 \big)\hat{j} + \big(\frac{4}{3}\ + 1 \big)\hat{k}\\ & \quad = -\frac{2}{3} \hat{i} - \frac{4}{3} \hat{j} + \frac{7}{3} \hat{k} \end{split}\]
المكونات هي C x =\(-\frac{2}{3}\)، C y =\(-\frac{4}{3}\)، و C z =\(\frac{7}{3}\)، والاستعاضة في المعادلة 2.5.6 تعطي
\[C = \sqrt{C_{x}^{2} + C_{y}^{2} + C_{z}^{2}} = \sqrt{\left(-\dfrac{2}{3}\right)^{2} + \left(-\dfrac{4}{3}\right)^{2} + \left(\dfrac{7}{3}\right)^{2}} = \sqrt{\frac{23}{3}} \ldotp\]
بدءًا من نزل التزلج، يذهب المتزلج الريفي على الثلج لمسافة 5.0 كم شمالًا، ثم 3.0 كم غربًا، وأخيرًا 4.0 كم جنوب غرب قبل أخذ قسط من الراحة. ابحث عن إجمالي متجه الإزاحة بالنسبة إلى النزل عندما يكون في نقطة الراحة. إلى أي مدى وفي أي اتجاه يجب أن يتزلج من نقطة الراحة للعودة مباشرة إلى النزل؟
إستراتيجيةنفترض نظام إحداثيات مستطيل مع الأصل في نزل التزلج ومتجه الوحدة الذي\(\hat{i}\) يشير إلى الشرق ومتجه الوحدة الذي\(\hat{j}\) يشير إلى الشمال. هناك ثلاث عمليات نزوح:\(\vec{D}_{1}\)،\(\vec{D}_{2}\)، و\(\vec{D}_{3}\). نحدد مقاييسها على النحو D 1 = 5.0 كم، D 2 = 3.0 كم، و D 3 = 4.0 كم. نحدد اتجاهاتها وهي الزوايا\(\theta_{1}\) = 90 درجة،\(\theta_{2}\) = 180 درجة، و\(\theta_{3}\) = 180 درجة + 45 درجة = 225 درجة. نقوم بحل كل متجه للإزاحة بمكوناته العددية ونستبدل المكونات في المعادلة 2.6.5 للحصول على المكونات العددية للإزاحة الناتجة\(\vec{D}\) من النزل إلى نقطة الراحة. في طريق العودة من نقطة الراحة إلى النزل، يكون الإزاحة\(\vec{B}\) = −\(\vec{D}\). أخيرًا، نجد حجم واتجاه\(\vec{B}\).
الحلالمكونات العددية لناقلات الإزاحة هي
\[ \begin{cases} D_{1x} = D_{1} \cos \theta_{1} = (5.0\; km) \cos 90^{o} = 0 \\ D_{1y} = D_{1} \sin \theta_{1} = (5.0\; km) \sin 90^{o} = 5.0\; km \end{cases}\]
\[ \begin{cases} D_{2x} = D_{2} \cos \theta_{2} = (3.0\; km) \cos 180^{o} = -3.0 \;km\\ D_{2y} = D_{2} \sin \theta_{2} = (3.0\; km) \sin 180^{o} = 0 \end{cases}\]
\[ \begin{cases} D_{3x} = D_{3} \cos \theta_{3} = (4.0\; km) \cos 225^{o} = -2.8\; km \\ D_{3y} = D_{3} \sin \theta_{3} = (4.0\; km) \sin 225^{o} = -2.8\; km \end{cases}\]
المكونات العددية لناقل الإزاحة الصافي هي
\[ \begin{cases} D_{x} = D_{1x} + D_{2x} + D_{3x} = (0 - 3.0 - 2.8)km = -5.8\; km \\ D_{y} = D_{1y} + D_{2y} + D_{3y} = (5.0 + 0 - 2.8)km = + 2.2\; km \end{cases}\]
وبالتالي، فإن متجه الإزاحة الصافي للمتزلج هو\(\vec{D}\) = D x\(\hat{i}\) + D y\(\hat{j}\) = (−5.8\(\hat{i}\) + 2.2\(\hat{j}\)) كم. في طريق العودة إلى النزل، كانت نزوحته\(\vec{B}\) = −\(\vec{D}\) = (−5.8\(\hat{i}\) + 2.2\(\hat{j}\)) كم = (5.8\(\hat{i}\) - 2.2\(\hat{j}\)) كم. حجمها هو B =\(\sqrt{B_{x}^{2} + B_{y}^{2}}\) =\(\sqrt{(5.8)^{2} + (−2.2)^{2}}\) km = 6.2 كم وزاوية اتجاهها هي\(\theta\) = تان −1\(\left(\dfrac{−2.2}{5.8}\right)\) = −20.8°. لذلك، للعودة إلى النزل، يجب عليه السير لمسافة 6.2 كم في اتجاه حوالي 21 درجة جنوب الشرق.
الأهمية
لاحظ أنه لا توجد حاجة إلى رقم لحل هذه المشكلة بالطريقة التحليلية. الأرقام مطلوبة عند استخدام طريقة رسومية؛ ومع ذلك، يمكننا التحقق مما إذا كان حلنا منطقيًا من خلال رسمه، وهي خطوة نهائية مفيدة في حل أي مشكلة في المتجهات.
يركض عداء في رحلة من 200 خطوة متطابقة إلى أعلى التل ثم يركض على طول قمة التل 50.0 مترًا قبل أن يتوقف عند نافورة الشرب (الشكل\(\PageIndex{3}\)). متجه الإزاحة الخاص به من النقطة A في أسفل الدرجات إلى النقطة B عند النافورة يساوي\(\vec{D}_{AB}\) = (−90.0\(\hat{i}\) + 30.0\(\hat{j}\)) m، ما ارتفاع وعرض كل خطوة في الرحلة؟ ما هي المسافة الفعلية التي يغطيها العداء؟ إذا قام بعمل حلقة وعاد إلى النقطة A، فما هو متجه الإزاحة الصافي الخاص به؟
إستراتيجية
متجه الإزاحة\(\vec{D}_{AB}\) هو المجموع المتجه لمتجه الإزاحة الخاص بالعداء\(\vec{D}_{AT}\) على طول الدرج (من النقطة A في أسفل الدرج إلى النقطة T في أعلى الدرج) ومتجه الإزاحة الخاص به\(\vec{D}_{RB}\) على قمة التل (من النقطة T في أعلى الدرج إلى نافورة عند النقطة B). يجب أن نجد المكونات الأفقية والعمودية لـ\(\vec{D}_{TB}\). إذا كانت كل خطوة لها عرض w وارتفاع h،\(\vec{D}_{TB}\) يجب أن يكون طول المكون الأفقي 200 واط ويجب أن يكون طول المكون الرأسي 200 ساعة. المسافة الفعلية التي يقطعها العداء هي مجموع المسافة التي يجرها صعودًا على الدرج والمسافة 50.0 مترًا التي يجريها على طول قمة التل.
الحل
في نظام الإحداثيات الموضح في الشكل\(\PageIndex{3}\)، يكون متجه الإزاحة الخاص بالمهرول على قمة التل\(\vec{D}_{RB}\) = (−50.0 m)\(\hat{i}\). ناقل الإزاحة الصافي الخاص به هو
\[\vec{D}_{AB} = \vec{D}_{AT} + \vec{D}_{TB} \ldotp \nonumber\]
لذلك، فإن ناقل نزوحه\(\vec{D}_{TB}\) على طول الدرج هو
\[\begin{split} \vec{D}_{AT}& = \vec{D}_{AB} - \vec{D}_{TB} = (-90.0 \hat{i} + 30.0 \hat{j})m - (-50.0 m)\hat{i}) = [(-90.0 50.0) hat{i} + 30.0 \hat{j})]m \\ & = (-40.0 \hat{i} + 30.0 \hat{j})m \ldotp \end{split}\]
مكوناته العددية هي D Tax = −40.0 m و D Tay = 30.0 m، لذلك يجب أن يكون لدينا
\[200 w=|-40.0| \mathrm{m} \text { and } 200 h=30.0 \: \mathrm{m} \ldotp \nonumber\]
وبالتالي، فإن عرض الخطوة هو w\(\frac{40.0\; m}{200}\) = = 0.2 م = 20 سم، وارتفاع الخطوة هو w\(\frac{30.0\; m}{200}\) = 0.15 m = 15 سم. المسافة التي يغطيها العداء على طول الدرج هي
\[\vec{D}_{AT} = \sqrt{\vec{D}_{ATx}^{2} + \vec{D}_{ATy}^{2}} = \sqrt{(-40.0)^{2} + (30.0)^{2}}m = 50.0\; m \ldotp \nonumber\]
وبالتالي، فإن المسافة الفعلية التي يركضها هي D AT + D TB = 50.0 m + 50.0 m = 100.0 m، وعندما يصنع حلقة ويعود من النافورة إلى موضعه الأولي عند النقطة A، فإن المسافة الإجمالية التي يغطيها هي ضعف هذه المسافة، أو 200.0 م، ومع ذلك، فإن متجه الإزاحة الصافي الخاص به هو صفر، لأن عندما يكون موضعه النهائي هو نفس موضعه الأولي، تكون المكونات العددية لمتجه الإزاحة الصافي الخاص به صفرًا (المعادلة 2.4.4).
في العديد من الحالات المادية، نحتاج غالبًا إلى معرفة اتجاه المتجه. على سبيل المثال، قد نرغب في معرفة اتجاه متجه المجال المغناطيسي عند نقطة ما أو اتجاه حركة الجسم. لقد قلنا بالفعل أن الاتجاه يُعطى بواسطة متجه الوحدة، وهو كيان بلا أبعاد - أي أنه لا يحتوي على وحدات مادية مرتبطة به. عندما يقع المتجه المعني على طول أحد المحاور في نظام الإحداثيات الديكارتية، تكون الإجابة بسيطة، لأن متجه الوحدة الخاص به يكون إما موازيًا أو مضادًا لاتجاه متجه الوحدة للمحور. على سبيل المثال، اتجاه المتجه\(\vec{d}\) = -5 m\(\hat{i}\) هو متجه الوحدة\(\vec{d}\) = -\(\hat{i}\). القاعدة العامة لإيجاد متجه\(\vec{V}\) الوحدة لأي متجه\(\vec{V}\) هي تقسيمه على حجمه V:
\[\widehat{\mathbf{V}}=\frac{\overrightarrow{\mathbf{V}}}{V} \label{2.26} \cdot \]
نرى من هذا التعبير أن متجه الوحدة للاتجاه هو بالفعل بلا أبعاد لأن البسط والمقام في المعادلة\ ref {2.26} لهما نفس الوحدة المادية. بهذه الطريقة، تسمح لنا المعادلة\ ref {2.26} بالتعبير عن متجه الوحدة من حيث متجه الوحدة للمحاور. يوضح المثال التالي هذا المبدأ.
إذا كان متجه السرعة للقافلة العسكرية في المثال 2.6.1 هو\(\vec{v}\) = (4.000\(\hat{i}\) + 3.000\(\hat{j}\) + 0.100\(\hat{k}\)) كم/ساعة، فما هو متجه الوحدة لاتجاه حركتها.
إستراتيجيةمتجه الوحدة لاتجاه حركة القافلة هو متجه\(\hat{v}\) الوحدة الموازي لمتجه السرعة. يتم الحصول على متجه الوحدة بقسمة المتجه على حجمه، وفقًا للمعادلة\ ref {2.26}.
الحلحجم المتجه\(\vec{v}\) هو
\[v = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}} = \sqrt{4.000^{2} + 3.000^{2} + 0.100^{2}}km/h = 5.001\; km/h \ldotp \nonumber\]
للحصول على متجه الوحدة\(\hat{v}\)، قم\(\vec{v}\) بالقسمة على حجمه:
\[\begin{split} \hat{v}& = \frac{\vec{v}}{v} = \frac{(4.000 \hat{i} + 3.00 \hat{j} + 0.100 \hat{k})km/h}{5.001\; km/h} \\ & = \frac{(4.000 \hat{i} + 3.000 \hat{j} + 0.1100 \hat{k})}{5.001} \\ & = \frac{4.000}{5.001} \hat{i} + \frac{3.000}{5.001} \hat{j} + \frac{0.100}{5.001} \hat{k} \\ & = (79.98 \hat{i} + 59.99 \hat{j} + 2.00 \hat{k}) \times 10^{-2} \ldotp \end{split}\]
الدلالةلاحظ أنه عند استخدام الطريقة التحليلية مع الآلة الحاسبة، يُنصح بإجراء العمليات الحسابية إلى ثلاث خانات عشرية على الأقل ثم تقريب الإجابة النهائية إلى العدد المطلوب من الأرقام المهمة، وهي الطريقة التي أجرينا بها العمليات الحسابية في هذا المثال. إذا أنهيت إجابتك الجزئية مبكرًا جدًا، فإنك تخاطر بحدوث خطأ عددي كبير في إجابتك النهائية، وقد تكون بعيدة عن الإجابة الدقيقة أو عن القيمة المقاسة في التجربة.
تحقق من أن المتجه الذي\(\hat{v}\) تم الحصول عليه في المثال\(\PageIndex{3}\) هو بالفعل متجه وحدة عن طريق حساب حجمه. إذا كانت القافلة في المثال 2.6.1 تتحرك عبر أرض صحراوية مسطحة - أي إذا كان المكون الثالث لسرعتها صفرًا - فما متجه الوحدة لاتجاه حركتها؟ ما الاتجاه الجغرافي الذي تمثله؟


