7.4: معادلات الخطوط المستقيمة الرأسية والأفقية
- Page ID
- 166928
معادلة الخط العمودي هي من النموذج\(x = c\)، حيث\(c\) يوجد أي رقم حقيقي. سيتقاطع الخط العمودي دائمًا مع\(x\) المحور −عند هذه النقطة\((c, 0)\). ميل الخط العمودي غير محدد.
ابحث عن ميل الخط\(x = 4\) وارسم الخط بيانيًا.
الحل
\(x = 4\)هو الرسم البياني لخط عمودي كما هو موضح في الشكل أدناه.
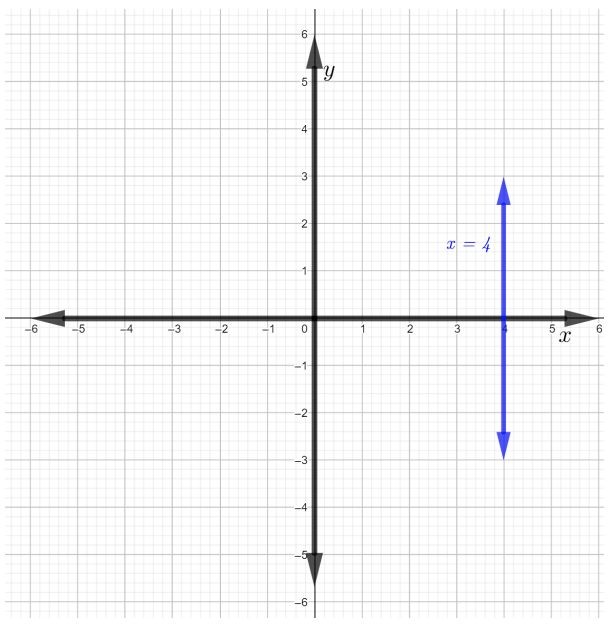
للعثور على ميل الخط،\(x = 4\) اختر أي نقطتين مميزتين على الخط. دع النقاط تكون\((4, −1)\) و\((4, 3)\). باستخدام صيغة ميل الخط،
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3 − (−1)}{4 − 4} &\text{Substitute values} \\ &= \dfrac{4}{0} &\text{Simplify} \end{array}\)
الآن، إذا\(4\)\(0\) قُسِّمت على، فهذا يعادل طرح السؤال التالي: «ما العدد الذي يساوي الصفر\(4\)؟» الجواب هو أنه لا يوجد مثل هذا الرقم. القسمة على الصفر غير محددة، ومنحدر الخط العمودي\(x = 4\) غير محدد.
معادلة الخط الأفقي هي من النموذج\(y = k\)، حيث\(k\) يوجد أي رقم حقيقي. سيتقاطع الخط الأفقي دائمًا مع\(y\) المحور −عند النقطة\((0, k)\). ميل الخط الأفقي هو صفر.
أوجد ميل الخط الذي يمر عبر النقطتين\((−3, −2)\) و\((4, −2)\). ارسم النقاط وارسم الخط الذي يمر عبرها.
الحل
استخدم ميل الصيغة الخطية. وهكذا،
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{(−2) − (−2)}{4 − (−3)} &\text{Substitute values} \\ &= \dfrac{0}{7} &\text{Simplify} \\ &= 0 &\text{\(0\)مقسومًا على أي رقم غير صفري يساوي صفر}\ end {array}\)
لذلك، فإن الخط الذي يمر عبر النقطتين المعطاة هو خط أفقي، مع ميل يساوي صفرًا، كما هو موضح في الشكل أدناه.
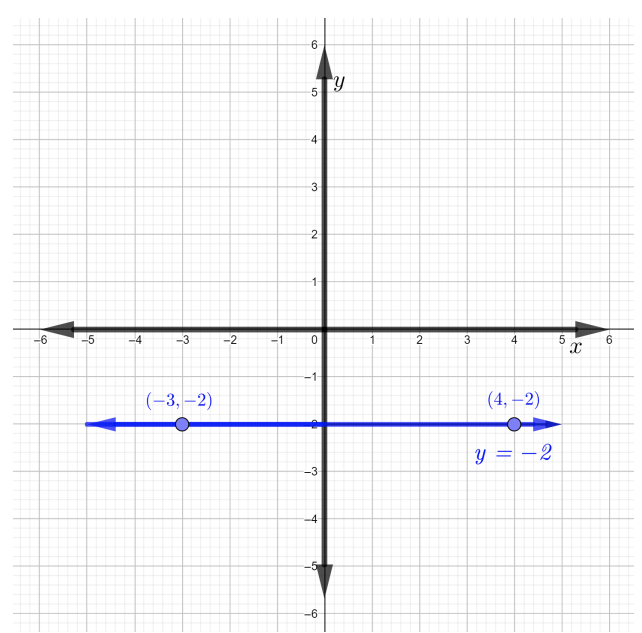
ارسم الخط البياني\(y − 3 = 0\) وابحث عن ميله.
الحل
\(y − 3 = 0\)يمكن كتابة الخط كـ\(y = 3\) (أضف\(3\) إلى جانبي المعادلة). الخط\(y = 3\) هو خط أفقي، كما هو موضح في الشكل أدناه.
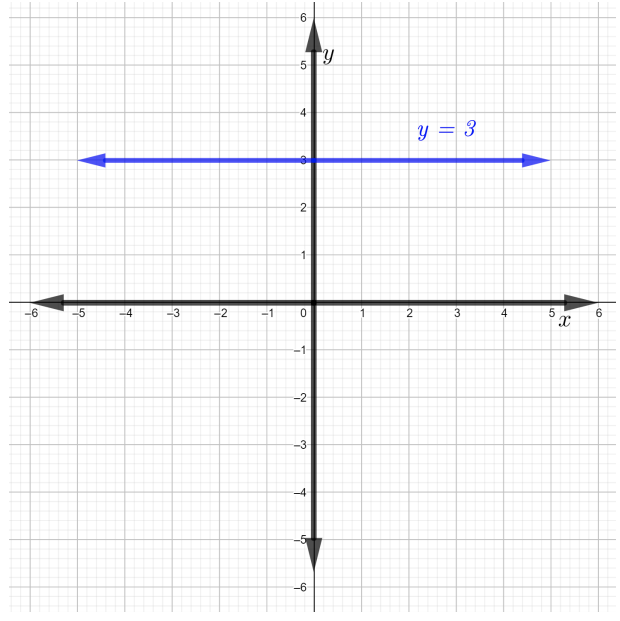
الآن، للعثور على المنحدر، اختر أي نقطتين متميزتين على الخط\(y = 3\). ضع في اعتبارك النقاط\((0, 3)\) و\((3, 3)\). وهكذا،
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3-3}{3-0} &\text{Substitute values} \\ &= \dfrac{0}{2} &\text{Simplify} \\ &= 0 &\text{\(0\)مقسومًا على أي رقم غير صفري يساوي صفر}\ end {array}\)
لذلك، ميل الخط المعطى هو\(m = 0.\)
أوجد ميل كل خط.
- \(x = −\dfrac{1}{2}\)
- \(y − 1 = 0\)
- \(x + 7 = 10\)
- \(y + 2 = −9\)
- أوجد ميل الخط الذي يمر عبر النقطتين\((−4, 1)\) و\((2, 1)\). ارسم النقاط وارسم الخط الذي يمر عبرها.
- أوجد ميل الخط الذي يمر عبر النقطتين\((−3, 5)\) و\((−3, −7)\). ارسم النقاط وارسم الخط الذي يمر عبرها.


