10.1: حل المعادلات التربيعية باستخدام خاصية الجذر التربيعي
- Page ID
- 200209
في نهاية هذا القسم، ستكون قادرًا على:
- حل المعادلات التربيعية للنموذج\(ax^2=k\) باستخدام خاصية الجذر التربيعي
- حل المعادلات التربيعية للنموذج\(a(x−h)^2=k\) باستخدام خاصية الجذر التربيعي
- قم بالتبسيط:\(\sqrt{75}\).
- قم بالتبسيط:\(\sqrt{\dfrac{64}{3}}\)
- عامل:\(4x^{2} − 12x + 9\).
المعادلات التربيعية هي معادلات من الشكل\(ax^{2} + bx + c = 0\) والمكان\(a \neq 0\). وهي تختلف عن المعادلات الخطية من خلال تضمين مصطلح مع رفع المتغير إلى القوة الثانية. نستخدم طرقًا مختلفة لحل المعادلات التربيعية s مقارنة بالمعادلات الخطية، لأن مجرد جمع الحدود وطرحها وضربها وقسمتها لن يعزل المتغير.
لقد رأينا أن بعض المعادلات التربيعية يمكن حلها عن طريق التحليل. في هذا الفصل، سوف نستخدم ثلاث طرق أخرى لحل المعادلات التربيعية.
حل المعادلات التربيعية للنموذج\(ax^2=k\) باستخدام خاصية الجذر التربيعي
لقد قمنا بالفعل بحل بعض المعادلات التربيعية عن طريق التحليل. دعونا نراجع كيف استخدمنا التحليل لحل المعادلة التربيعية\(x^{2} = 9\).
\[\begin{array}{ll} {}&{x^2=9}\\ {\text{Put the equation in standard form.}}&{x^2−9=0}\\ {\text{Factor the left side.}}&{(x - 3)(x + 3) = 0}\\ {\text{Use the Zero Product Property.}}&{(x - 3) = 0, (x + 3) = 0}\\ {\text{Solve each equation.}}&{x = 3, x = -3}\\ {\text{Combine the two solutions into} \pm \text{form}}&{x=\pm 3}\\ \nonumber \end{array}\]
(تتم قراءة الحل «\(x\)يساوي الموجب أو السلبي»\(3\).)
يمكننا بسهولة استخدام التحليل لإيجاد حلول لمعادلات متشابهة، مثل\(x^{2} = 25\)،\(x^{2}=16\)\(16\) ولأن\(25\)، مربعات مثالية. ولكن ماذا يحدث عندما تكون لدينا معادلة مثل\(x^{2}=7\)؟ نظرًا لأنه\(7\) ليس مربعًا مثاليًا، فلا يمكننا حل المعادلة عن طريق التحليل.
هذه المعادلات كلها في الشكل\(x^{2}=k\).
لقد حددنا الجذر التربيعي للرقم بهذه الطريقة:
إذا كان\(n^{2} = m\)، إذن\(n\) هو الجذر التربيعي لـ\(m\).
هذا يؤدي إلى خاصية الجذر التربيعي.
إذا\(x^{2}=k\)\(k \geq 0\)، ثم\(x = \sqrt{k}\) أو\(x = -\sqrt{k}\).
لاحظ أن خاصية الجذر التربيعي تعطي حلين لمعادلة الشكل\(x^2=k\): الجذر التربيعي الرئيسي لـ k وعكسه. يمكننا أيضًا كتابة الحل كـ\(x=\pm \sqrt{k}\)
الآن، سنحل المعادلة\(x^{2} = 9\) مرة أخرى، هذه المرة باستخدام خاصية الجذر التربيعي.
\[\begin{array}{ll} {}&{x^{2} = 9}\\ {\text{Use the Square Root Property.}}&{x = \pm\sqrt{9}}\\ {\text{Simplify the radical.}}&{x = \pm 3}\\ {\text{Rewrite to show the two solutions.}}&{x = 3, x = −3}\\ \nonumber \end{array}\]
ماذا يحدث عندما لا يكون الثابت مربعًا مثاليًا؟ دعونا نستخدم خاصية الجذر التربيعي لحل المعادلة\(x^2=7\).
\[\begin{array} {ll} {\text{Use the Square Root Property. }}&{x = \pm\sqrt{7}}\\ {\text{Rewrite to show two solutions.}}&{x = \sqrt{7}, x = −\sqrt{7}}\\ {\text{We cannot simplify} \sqrt{7} \text{ so we leave the answer as a radical.}}&{}\\ \nonumber \end{array}\]
حل:\(x^{2} = 169\)
- إجابة
-
\[\begin{array}{ll} {}&{x^2=169}\\ {\text{Use the Square Root Property.}}&{x=\pm\sqrt{169}}\\ {\text{Simplify the radical.}}&{x = \pm13}\\{\text{Rewrite to show two solutions.}}&{x = 13, x = −13}\\ \nonumber \end{array}\]
حل:\(x^2=81\)
- إجابة
-
x=9، x=−9
حل:\(y^{2} = 121\)
- إجابة
-
y = 1.1، y = −11
كيفية حل المعادلة التربيعية للنموذج\(ax^{2} = k\) باستخدام خاصية الجذر التربيعي
حل:\(x^{2} − 48 = 0\)
- إجابة




حل:\(x^{2} − 50 = 0\)
- إجابة
-
\(x = 5\sqrt{2}, x = −5\sqrt{2}\)
حل:\(y^{2} − 27 = 0\)
- إجابة
-
\(y = 3\sqrt{3}, x = −3\sqrt{3}\)
- اعزل الحد التربيعي واجعل معامله واحدًا.
- استخدم خاصية الجذر التربيعي.
- قم بتبسيط الراديكالية.
- تحقق من الحلول.
لاستخدام خاصية الجذر التربيعي، يجب أن يساوي معامل المصطلح المتغير 1. في المثال التالي، يجب أن نقسم كلا طرفي المعادلة على 5 قبل استخدام خاصية الجذر التربيعي.
حل:\(5m^2=80\)
- إجابة
-
يتم عزل المصطلح التربيعي. \(5m^2=80\) اقسم على 5 لجعل المعامل 1. \(\frac{5m^2}{5}=\frac{80}{5}\) قم بالتبسيط. \(m^2=16\) استخدم خاصية الجذر التربيعي. \(m=\pm\sqrt{16}\) قم بتبسيط الراديكالية. \(m=\pm 4\) أعد الكتابة لإظهار حلين. m=4، m=−4 تحقق من الحلول.
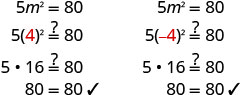
حل:\(2x^2=98\).
- إجابة
-
x=7، x=−7
حل:\(3z^2=108\).
- إجابة
-
z=6، z = −6
بدأت خاصية الجذر التربيعي بالنص على «إذا\(k\ge 0\)»\(x^2=k\) و «. ماذا سيحدث إذا\(k<0\)؟ سيكون هذا هو الحال في المثال التالي.
حل:\(q^2+24=0\).
- إجابة
-
\[\begin{array}{ll} {}&{q^2=24}\\ {\text{Isolate the quadratic term.}}&{q^2=−24}\\ {\text{Use the Square Root Property.}}&{q=\pm\sqrt{-24}}\\ {\text{The} \sqrt{-24} \text{is not a real number}}& {\text{There is no real solution}}\\ \nonumber \end{array}\]
حل:\(c^2+12=0\).
- إجابة
-
لا يوجد حل حقيقي
حل:\(d^2+81=0\).
- إجابة
-
لا يوجد حل حقيقي
حل:\(\frac{2}{3}u^2+5=17\).
- إجابة
-
\(\frac{2}{3}u^2+5=17\) اعزل الحد التربيعي. \(\frac{2}{3}u^2=12\)
اضرب\(\frac{3}{2}\) في لجعل المعامل 1. \(\frac{3}{2}·\frac{2}{3}u^2=\frac{3}{2}·12\) قم بالتبسيط. \(u^2=18\) استخدم خاصية الجذر التربيعي. \(u=\pm\sqrt{18}\) قم بتبسيط الراديكالية. \(u=\pm\sqrt{9}\sqrt{2}\) قم بالتبسيط. \(u=\pm3\sqrt{2}\) أعد الكتابة لإظهار حلين. \(u=3\sqrt{2}\)،\(u=−3\sqrt{2}\) تحقق.
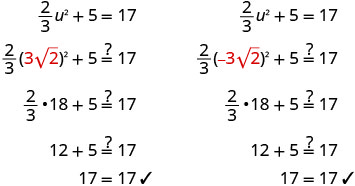
حل:\(\frac{1}{2}x^2+4=24\)
- إجابة
-
\(x=2\sqrt{10}\)،\(x=−2\sqrt{10}\)
حل:\(\frac{3}{4}y^2−3=18\).
- إجابة
-
\(y=2\sqrt{7}\)،\(y=−2\sqrt{7}\)
قد تحتوي حلول بعض المعادلات على كسور داخل الجذور. عندما يحدث هذا، يجب علينا ترشيد القاسم.
حل:\(2c^2−4=45\).
- إجابة
-
\(2c^2−4=45\) اعزل الحد التربيعي. \(2c^2=49\) اقسم على 2 لجعل المعامل 1. \(\frac{2c^2}{2}=\frac{49}{2}\) قم بالتبسيط. \(c^2=\frac{49}{2}\) استخدم خاصية الجذر التربيعي. \(c=\pm\frac{\sqrt{49}}{\sqrt{2}}\) قم بتبسيط الراديكالية. \(c=\pm\frac{\sqrt{49}}{\sqrt{2}}\) قم بترشيد المقام. \(c=\pm\frac{\sqrt{49}\sqrt{2}}{\sqrt{2}\sqrt{2}}\) قم بالتبسيط. \(c=\pm\frac{7\sqrt{2}}{2}\) أعد الكتابة لإظهار حلين. \(c=\frac{7\sqrt{2}}{2}\)،\(c=−\frac{7\sqrt{2}}{2}\) تحقق. نترك الشيك لك.
حل:\(5r^2−2=34\).
- إجابة
-
\(r=\frac{6\sqrt{5}}{5}\)،\(r=−\frac{6\sqrt{5}}{5}\)
حل:\(3t^2+6=70\).
- إجابة
-
\(t=\frac{8\sqrt{3}}{3}\)،\(t=−\frac{8\sqrt{3}}{3}\)
حل المعادلات التربيعية للنموذج\(a(x-h)^2=k\) باستخدام خاصية الجذر التربيعي
يمكننا استخدام خاصية الجذر التربيعي لحل معادلة مثل\((x−3)^2=16\)، أيضًا. سوف نتعامل مع المعادلة ذات الحدين بأكملها (x−3) على أنها الحد التربيعي.
حل:\((x−3)^2=16\).
- إجابة
-
\((x−3)^2=16\) استخدم خاصية الجذر التربيعي. \(x−3=\pm\sqrt{16}\) قم بالتبسيط. \(x−3=\pm 4\) اكتب في صورة معادلتين. \(x−3=4\)،\(x−3=−4\) حل. x=7، x=−1 تحقق.
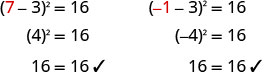
حل:\((q+5)^2=1\).
- إجابة
-
q=−6، q=−4
حل:\((r−3)^2=25\).
- إجابة
-
r=8، r=−2
حل:\((y−7)^2=12\).
- إجابة
-
\((y−7)^2=12\). استخدم خاصية الجذر التربيعي. \(y−7=\pm\sqrt{12}\) قم بتبسيط الراديكالية. \(y−7=\pm2\sqrt{3}\) حل من أجلك. \(y=7\pm2\sqrt{3}\) أعد الكتابة لإظهار حلين. \(y=7+2\sqrt{3}\)،\(y=7−2\sqrt{3}\) تحقق.

حل:\((a−3)^2=18\).
- إجابة
-
\(a=3+3\sqrt{2}\)،\(a=3−3\sqrt{2}\)
حل:\((b+2)^2=40\).
- إجابة
-
\(b=−2+2\sqrt{10}\)،\(b=−2−2\sqrt{10}\)
حل:\((x−\frac{1}{2})^2=\frac{5}{4}\).
- إجابة
-
\((x−\frac{1}{2})^2=\frac{5}{4}\) استخدم خاصية الجذر التربيعي. \((x−\frac{1}{2})=\pm\sqrt\frac{5}{4}\) أعد كتابة الجذر في صورة جزء من الجذور التربيعية. \((x−\frac{1}{2})=\pm\frac{\sqrt{5}}{\sqrt{4}}\) قم بتبسيط الراديكالية. \((x−\frac{1}{2})=\pm\frac{\sqrt{5}}{2}\) حل لـ x. \(x=\frac{1}{2}+\pm\frac{\sqrt{5}}{2}\) أعد الكتابة لإظهار حلين. \(x=\frac{1}{2}+\frac{\sqrt{5}}{2}\)،\(x=\frac{1}{2}−\frac{\sqrt{5}}{2}\) تحقق. نترك الشيك لك
حل:\((x−\frac{1}{3})^2=\frac{5}{9}\).
- إجابة
-
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}\)،\(x=\frac{1}{3}−\frac{\sqrt{5}}{3}\)
حل:\((y−\frac{3}{4})^2=\frac{7}{16}\).
- إجابة
-
\(y=\frac{3}{4}+\frac{\sqrt{7}}{4}\)،\(y=\frac{3}{4}−\frac{\sqrt{7}}{4}\)،
سنبدأ الحل للمثال التالي عن طريق عزل المعادلة ذات الحدين.
حل:\((x−2)^2+3=30\).
- إجابة
-
\((x−2)^2+3=30\) اعزل المصطلح ذي الحدين. \((x−2)^2=27\) استخدم خاصية الجذر التربيعي. \(x−2=\pm\sqrt{27}\) قم بتبسيط الراديكالية. \(x−2=\pm3\sqrt{3}\) حل لـ x. \(x=2+\pm3\sqrt{3}\) \(x−2=\pm3\sqrt{3}\) \(x=2+3\sqrt{3}\)،\(x=2−3\sqrt{3}\) تحقق. نترك الشيك لك
حل:\((a−5)^2+4=24\).
- إجابة
-
\(a=5+2\sqrt{5}\)،\(a=5−2\sqrt{5}\)
حل:\((b−3)^2−8=24\).
- إجابة
-
\(b=3+4\sqrt{2}\)،\(b=3−4\sqrt{2}\)
حل:\((3v−7)^2=−12\).
- إجابة
-
\((3v−7)^2=−12\) استخدم خاصية الجذر التربيعي. \(3v−7=\pm\sqrt{−12}\) \(\sqrt{−12}\)هذا ليس رقمًا حقيقيًا. لا يوجد حل حقيقي.
حل:\((3r+4)^2=−8\).
- إجابة
-
لا يوجد حل حقيقي
لا يبدو أن الجوانب اليسرى من المعادلات في المثالين التاليين من الشكل\(a(x−h)^2\). لكنها عبارة عن وحدات ثلاثية مربعة مثالية، لذلك سننظر في وضعها بالشكل الذي نحتاجه.
حل:\(p^2−10p+25=18\).
- إجابة
-
الجانب الأيسر من المعادلة هو مربع كامل ثلاثي الحدود. سنقوم بأخذها في الاعتبار أولاً.
\(p^2−10p+25=18\) عامل مربع ثلاثي الحدود المثالي. \((p−5)^2=18\) استخدم خاصية الجذر التربيعي. \(p−5=\pm\sqrt{18}\) قم بتبسيط الراديكالية. \(p−5=\pm3\sqrt{2}\) حل لـ p. \(p=5\pm3\sqrt{2}\) أعد الكتابة لإظهار حلين. \(p=5+3\sqrt{2}\)،\(p=5−3\sqrt{2}\) تحقق. نترك الشيك لك.
حل:\(x^2−6x+9=12\).
- إجابة
-
\(x=3+2\sqrt{3}\)،\(x=3−2\sqrt{3}\)
حل:\(y^2+12y+36=32\).
- إجابة
-
\(y=−6+4\sqrt{2}\)،\(y=−6−4\sqrt{2}\)
حل:\(4n^2+4n+1=16\).
- إجابة
-
مرة أخرى، نلاحظ أن الجانب الأيسر من المعادلة هو مربع كامل ثلاثي الحدود. سنقوم بأخذها في الاعتبار أولاً.
\(4n^2+4n+1=16\) عامل مربع ثلاثي الحدود المثالي. \((2n+1)^2=16\) استخدم خاصية الجذر التربيعي. \((2n+1)=\pm\sqrt{16}\) قم بتبسيط الراديكالية. \((2n+1)=\pm4\) حل لـ n. \(2n=−1\pm4\) قسّم كل جانب على 2. \(\frac{2n}{2}=\frac{−1\pm4}{2}\)
\(n=\frac{−1\pm4}{2}\)
أعد الكتابة لإظهار حلين. \(n=\frac{−1+4}{2}\)،\(n=\frac{−1−4}{2}\) قم بتبسيط كل معادلة. \(n=\frac{3}{2}\)،\(n=−\frac{5}{2}\) تحقق.
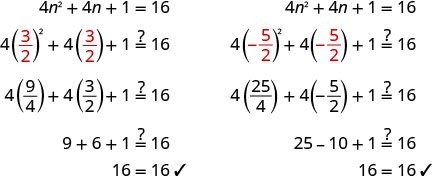
حل:\(9m^2−12m+4=25\).
- إجابة
-
\(m=\frac{7}{3}\)،\(m=−1\)
حل:\(16n^2+40n+25=4\).
- إجابة
-
\(n=−\frac{3}{4}\), \(n=−\frac{7}{4}\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل المعادلات التربيعية:
- حل المعادلات التربيعية: الحل بأخذ الجذور التربيعية
- استخدام الجذور التربيعية لحل المعادلات التربيعية
- حل المعادلات التربيعية: طريقة الجذر التربيعي
المفاهيم الرئيسية
- خاصية الجذر التربيعي
إذا\(x^2=k\)\(k\ge 0\)، ثم،\(x=\sqrt{k}\) أو\(x=−\sqrt{k}\).
مسرد المصطلحات
- معادلة تربيعية
- المعادلة التربيعية هي معادلة الشكل\(ax^2+bx+c=0\) حيث\(a \ne 0\).
- خاصية الجذر التربيعي
- تنص خاصية الجذر التربيعي على أنه\(x^2=k\)، إذا\(k\ge 0\)، ثم،\(x=\sqrt{k}\) أو\(x=−\sqrt{k}\).


