9.4: اضرب الجذور التربيعية

Last updated
Save as PDF

Page ID: 200122

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

اضرب الجذور المربعة
استخدم الضرب متعدد الحدود لضرب الجذور التربيعية

ملاحظة

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

تبسيط: (3 وحدات) (8 فولت).
إذا فاتتك هذه المشكلة، راجع المثال 6.2.31.
التبسيط: 6 (12-7n).
إذا فاتتك هذه المشكلة، راجع المثال 6.3.1.
تبسيط: (2+أ) (4−أ).
إذا فاتتك هذه المشكلة، راجع المثال 6.3.34.

اضرب الجذور المربعة

لقد استخدمنا خاصية المنتج لـ Square Roots لتبسيط الجذور التربيعية عن طريق إزالة العوامل المربعة المثالية. تقول خاصية المنتج لـ سكوير روتس

\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]

يمكننا استخدام خاصية المنتج لـ Square Roots «في الاتجاه المعاكس» لمضاعفة الجذور التربيعية.

\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]

تذكر أننا نفترض أن جميع المتغيرات أكبر من أو تساوي الصفر.

سنعيد كتابة خاصية المنتج لـ Square Roots حتى نرى كلا الطريقتين معًا.

تعريف: خاصية المنتج للجذور المربعة

إذا كانت a و b أرقامًا حقيقية غير سالبة، إذن

$\sqrt{ab}=\sqrt{a}·\sqrt{b}$و$\sqrt{a}·\sqrt{b}=\sqrt{ab}$.

حتى نتمكن من التكاثر$\sqrt{3}·\sqrt{5}$ in this way:

\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]

في بعض الأحيان يمنحنا المنتج مربعًا مثاليًا:

\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]

حتى عندما لا يكون المنتج مربعًا مثاليًا، يجب علينا البحث عن عوامل المربع المثالي وتبسيط الراديكالية كلما أمكن ذلك.

ضرب الجذور بمعاملات يشبه إلى حد كبير ضرب المتغيرات بمعاملات. لضرب 4x·3y، نضرب المعاملات معًا ثم المتغيرات. والنتيجة هي 12xy. ضع ذلك في الاعتبار أثناء قيامك بهذه الأمثلة.

مثال$\PageIndex{1}$

قم بالتبسيط:

$\sqrt{2}·\sqrt{6}$
$(4\sqrt{3})(2\sqrt{12})$.

إجابة

1.	$\sqrt{2}·\sqrt{6}$
اضرب باستخدام خاصية المنتج.	$\sqrt{12}$
قم بتبسيط الراديكالية.	$\sqrt{4}·\sqrt{3}$
قم بالتبسيط.	$2\sqrt{3}$
2.	$(4\sqrt{3})(2\sqrt{12})$
اضرب باستخدام خاصية المنتج.	$8\sqrt{36}$
قم بتبسيط الراديكالية.	$8·6$
قم بالتبسيط.	$48$

مثال$\PageIndex{2}$

قم بالتبسيط:

$\sqrt{3}·\sqrt{6}$
$(2\sqrt{6})(3\sqrt{12})$.

إجابة

$3\sqrt{2}$
$36\sqrt{2}$

مثال$\PageIndex{3}$

قم بالتبسيط:

$\sqrt{5}·\sqrt{10}$
$(6\sqrt{3})(5\sqrt{6})$

إجابة

$5\sqrt{2}$
$90\sqrt{2}$

مثال$\PageIndex{4}$

قم بالتبسيط:$(6\sqrt{2})(3\sqrt{10})$

إجابة

	$(6\sqrt{2})(3\sqrt{10})$
اضرب باستخدام خاصية المنتج.	$18\sqrt{20}$
قم بتبسيط الراديكالية.	$18\sqrt{4}·\sqrt{5}$
قم بالتبسيط.	$18·2·\sqrt{5}$
	$36\sqrt{5}$

مثال$\PageIndex{5}$

قم بالتبسيط:$(3\sqrt{2})(2\sqrt{30})$

إجابة: $12\sqrt{15}$

مثال$\PageIndex{6}$

قم بالتبسيط:$(3\sqrt{3})(3\sqrt{6})$.

إجابة: $27\sqrt{2}$

عندما نضطر إلى مضاعفة الجذور التربيعية، نجد المنتج أولاً ثم نزيل أي عوامل مربعة مثالية.

مثال$\PageIndex{7}$

قم بالتبسيط:

$(\sqrt{8x^3})(\sqrt{3x})$
$(\sqrt{20y^2})(\sqrt{5y^3})$

إجابة

1.	$(\sqrt{8x^3})(\sqrt{3x})$
اضرب باستخدام خاصية المنتج.	$\sqrt{24x^4}$
قم بتبسيط الراديكالية.	$\sqrt{4x^4}·\sqrt{6}$
قم بالتبسيط.	$2x^2\sqrt{6}$
2.	$(\sqrt{20y^2})(\sqrt{5y^3})$
اضرب باستخدام خاصية المنتج.	$\sqrt{100y^5}$
قم بتبسيط الراديكالية.	$10y^2\sqrt{y}$

مثال$\PageIndex{8}$

قم بالتبسيط:

$(\sqrt{6x^3})(\sqrt{3x})$
$(\sqrt{2y^3})(\sqrt{50y^2})$.

إجابة

$3x^2\sqrt{2}$
$10y^2\sqrt{y}$

مثال$\PageIndex{9}$

قم بالتبسيط:

$(\sqrt{6x^5})(\sqrt{2x})$
$(\sqrt{12y^2})(\sqrt{3y^5})$

إجابة

$2x^3\sqrt{3}$
$6y^2\sqrt{y}$

مثال$\PageIndex{10}$

قم بالتبسيط:$(10\sqrt{6p^3})(3\sqrt{18p})$

إجابة

	$(10\sqrt{6p^3})(3\sqrt{18p})$
اضرب.	$30\sqrt{108p^4}$
قم بتبسيط الراديكالية.	$30\sqrt{36p^4}·\sqrt{3}$
	$30·6p^2·\sqrt{3}$
	$180p^2\sqrt{3}$

مثال$\PageIndex{11}$

قم بالتبسيط:$(\sqrt{62x^2})(8\sqrt{45x^4})$

إجابة: $144x^3\sqrt{10}$

مثال$\PageIndex{12}$

قم بالتبسيط:$(2\sqrt{6y^4})(12\sqrt{30y})$.

إجابة: $144y^2\sqrt{5y}$

مثال$\PageIndex{13}$

قم بالتبسيط:

$(\sqrt{2})^2$
$(−\sqrt{11})^2$.

إجابة

1.	$(\sqrt{2})^2$
أعد الكتابة كمنتج.	$(\sqrt{2})(\sqrt{2})$
اضرب.	$\sqrt{4}$
قم بالتبسيط.	2
2.	$(−\sqrt{11})^2$
أعد الكتابة كمنتج.	$(−\sqrt{11})(−\sqrt{11})$
اضرب.	$\sqrt{121}$
قم بالتبسيط.	11

مثال$\PageIndex{14}$

قم بالتبسيط:

$(\sqrt{12})^2$
$(−\sqrt{15})^2$.

إجابة

مثال$\PageIndex{15}$

قم بالتبسيط:

$(\sqrt{16})^2$
$(−\sqrt{20})^2$.

إجابة

نتائج المثال السابق تقودنا إلى هذه الخاصية.

تعريف: تربيع الجذر التربيعي

إذا كان الرقم a هو رقم حقيقي غير سالب، إذن

$(\sqrt{a})^2=a$

من خلال إدراك أن التربيع وأخذ الجذر التربيعي هما عمليتان «معاكستان»، يمكننا التبسيط$(\sqrt{2})^2$ والحصول على 2 على الفور. عندما نضرب الجذور التربيعية المتشابهة في الجزء (أ) من المثال التالي، يكون هذا هو نفس التربيع.

مثال$\PageIndex{16}$

قم بالتبسيط:

$(2\sqrt{3})(8\sqrt{3})$
$(3\sqrt{6})^2$.

إجابة

1.	$(2\sqrt{3})(8\sqrt{3})$
اضرب. تذكر،$(\sqrt{3}^2)$	16·3
قم بالتبسيط.	48
2.	$(3\sqrt{6})^2$
اضرب.	9·6
قم بالتبسيط.	54

مثال$\PageIndex{17}$

قم بالتبسيط:

$(6\sqrt{11})(5\sqrt{11})$
$(5\sqrt{8})^2$.

إجابة

مثال$\PageIndex{18}$

قم بالتبسيط:

$(3\sqrt{7})(10\sqrt{7})$
$(−4\sqrt{6})^2$.

إجابة

استخدم الضرب متعدد الحدود لضرب الجذور التربيعية

في الأمثلة القليلة التالية، سنستخدم خاصية التوزيع لضرب التعبيرات ذات الجذور التربيعية.

سنقوم أولاً بتوزيع الجذور التربيعية ثم تبسيطها عندما يكون ذلك ممكنًا.

مثال$\PageIndex{19}$

قم بالتبسيط:

$3(5−\sqrt{2})$
$\sqrt{2}(4−\sqrt{10})$.

إجابة

1.	$3(5−\sqrt{2})$
توزيع.	$15−3\sqrt{2})$
2.	$\sqrt{2}(4−\sqrt{10})$
توزيع.	$4\sqrt{2}−\sqrt{20}$
قم بالتبسيط.	$4\sqrt{2}−2\sqrt{5}$

مثال$\PageIndex{20}$

قم بالتبسيط:

$2(3−\sqrt{5})$
$\sqrt{3}(2−\sqrt{18})$.

إجابة

$6−2\sqrt{5}$
$2\sqrt{3}−3\sqrt{6}$

مثال$\PageIndex{21}$

قم بالتبسيط:

$6(2+\sqrt{6})$
$\sqrt{7}(1+\sqrt{14})$.

إجابة

$12+\sqrt{6}$
$\sqrt{7}+7\sqrt{2}$

مثال$\PageIndex{22}$

قم بالتبسيط:

$\sqrt{5}(7+2\sqrt{5})$
$\sqrt{6}(\sqrt{2}+\sqrt{18})$.

إجابة

1.	$\sqrt{5}(7+2\sqrt{5})$
قم بالتوزيع.	$7\sqrt{5}+2·5$
قم بالتبسيط.	$7\sqrt{5}+10$
	$10+7\sqrt{5}$
2.	$\sqrt{6}(\sqrt{2}+\sqrt{18})$
اضرب.	$\sqrt{12}+\sqrt{108}$
قم بالتبسيط.	$(\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})$
	$2\sqrt{3}+6\sqrt{3}$
اجمع مثل الراديكاليين.	$8\sqrt{3}$

مثال$\PageIndex{23}$

قم بالتبسيط:

$\sqrt{6}(1+3\sqrt{6})$
$\sqrt{12}(\sqrt{3}+\sqrt{24})$

إجابة

$18+\sqrt{6}$
$6+12\sqrt{2}$

مثال$\PageIndex{24}$

قم بالتبسيط:

$\sqrt{8}(2−5\sqrt{8})$
$\sqrt{14}(\sqrt{2}+\sqrt{42})$

إجابة

$−40+4\sqrt{2}$
$2\sqrt{7}+14\sqrt{3}$

عندما تعاملنا مع كثيرات الحدود، قمنا بضرب المقادير ذات الحدين في الحدود الثنائية. تذكر أن هذا أعطانا أربعة منتجات قبل أن نجمع أي شروط مماثلة. للتأكد من الحصول على جميع المنتجات الأربعة، قمنا بتنظيم عملنا - عادةً بطريقة FOIL.

مثال$\PageIndex{25}$

قم بالتبسيط:$(2+\sqrt{3})(4−\sqrt{3})$

إجابة

	$(2+\sqrt{3})(4−\sqrt{3})$
اضرب.	$8−2\sqrt{3}+4\sqrt{3}−3$
اجمع بين المصطلحات المتشابهة.	$5+2\sqrt{3}$

مثال$\PageIndex{26}$

قم بالتبسيط:$(1+\sqrt{6})(3−\sqrt{6})$.

إجابة: $−3+2\sqrt{6}$

مثال$\PageIndex{27}$

قم بالتبسيط:$(4−\sqrt{10})(2+\sqrt{10})$.

إجابة: $−2+2\sqrt{10}$

مثال$\PageIndex{28}$

قم بالتبسيط:$(3−2\sqrt{7})(4−2\sqrt{7})$.

إجابة

	$(3−2\sqrt{7})(4−2\sqrt{7})$
اضرب.	$12−6\sqrt{7}−8\sqrt{7}+4·7$
قم بالتبسيط.	$12−6\sqrt{7}−8\sqrt{7}+28$
اجمع بين المصطلحات المتشابهة.	$40−14\sqrt{7}$

مثال$\PageIndex{29}$

قم بالتبسيط:$(6−3\sqrt{7})(3+4\sqrt{7})$.

إجابة: $−66+15\sqrt{7}$

مثال$\PageIndex{30}$

قم بالتبسيط:$(2−3\sqrt{11})(4−\sqrt{11})$

إجابة: $41+14\sqrt{11}$

مثال$\PageIndex{31}$

قم بالتبسيط:$(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})$.

إجابة

	$3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})$
اضرب.	$3·2+12\sqrt{10}−\sqrt{10}−4·5$
قم بالتبسيط.	$6+12\sqrt{10}−\sqrt{10}−20$
اجمع بين المصطلحات المتشابهة.	$−14+11\sqrt{10}$

مثال$\PageIndex{32}$

قم بالتبسيط:$(5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})$

إجابة: $1+9\sqrt{21}$

مثال$\PageIndex{33}$

قم بالتبسيط:$(\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})$

إجابة: $−12−20\sqrt{3}$

مثال$\PageIndex{34}$

قم بالتبسيط:$(4−2\sqrt{x})(1+3\sqrt{x})$.

إجابة

	$(4−2\sqrt{x})(1+3\sqrt{x})$.
اضرب.	$4+12\sqrt{x}−2\sqrt{x}−6x$
اجمع بين المصطلحات المتشابهة.	$4+10\sqrt{x}−6x$

مثال$\PageIndex{35}$

قم بالتبسيط:$(6−5\sqrt{m})(2+3\sqrt{m})$.

إجابة: $12+8\sqrt{m}−15m$

مثال$\PageIndex{36}$

قم بالتبسيط:$(10+3\sqrt{n})(1−5\sqrt{n})$

إجابة: $10−47\sqrt{n}−15n$

لاحظ أن بعض المنتجات الخاصة جعلت عملنا أسهل عندما قمنا بضرب الحدين في وقت سابق. هذا صحيح عندما نضرب الجذور التربيعية أيضًا. تظهر صيغ المنتجات الخاصة التي استخدمناها أدناه.

التعريف: صيغ المنتجات الخاصة

\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]

سنستخدم صيغ المنتجات الخاصة في الأمثلة القليلة التالية. سنبدأ بصيغة المربعات ذات الحدين.

مثال$\PageIndex{37}$

قم بالتبسيط:

$(2+\sqrt{3})^2$
$(4−2\sqrt{5})^2$.

إجابة

تأكد من تضمين مصطلح 2ab عند تربيع معادلة ذات حدين.

	$.$
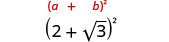
اضرب باستخدام نمط المربع ذي الحدين.	$.$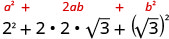
قم بالتبسيط.	$.$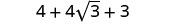
اجمع بين المصطلحات المتشابهة.	$.$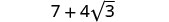

	$.$
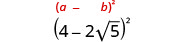
اضرب باستخدام نمط المربع ذي الحدين.	$.$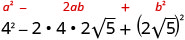
قم بالتبسيط.	$.$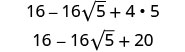
اجمع بين المصطلحات المتشابهة.	$.$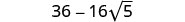

مثال$\PageIndex{38}$

قم بالتبسيط:

$(10+\sqrt{2})^2$
$(1+3\sqrt{6})^2$.

إجابة

$102+20\sqrt{2}$
$55+6\sqrt{6}$

التمارين الرياضية$\PageIndex{39}$

قم بالتبسيط:

$(6-\sqrt{5})^2$
$(9-2\sqrt{10})^2$.

إجابة

$41-12\sqrt{5}$
$121-36\sqrt{10}$

مثال$\PageIndex{40}$

قم بالتبسيط:$(1+3\sqrt{x})^2$.

إجابة

	$.$
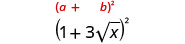
اضرب باستخدام نمط المربع ذي الحدين.	$.$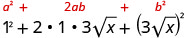
قم بالتبسيط.	$.$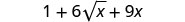

مثال$\PageIndex{41}$

قم بالتبسيط:$(2+5\sqrt{m})^2$.

إجابة: $4+20\sqrt{m}+25m$

مثال$\PageIndex{42}$

قم بالتبسيط:$(3−4\sqrt{n})^2$.

إجابة: $9−24\sqrt{n}+16n$

في المثالين التاليين، سنجد منتج المترافقات.

مثال$\PageIndex{43}$

قم بالتبسيط:$(4−\sqrt{2})(4+\sqrt{2})$.

إجابة

	$.$
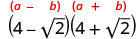
اضرب باستخدام نمط المربع ذي الحدين.	$.$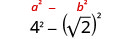
قم بالتبسيط.	$.$

مثال$\PageIndex{44}$

قم بالتبسيط:$(2−\sqrt{3})(2+\sqrt{3})$

إجابة: 1

مثال$\PageIndex{45}$

قم بالتبسيط:$(1+\sqrt{5})(1−\sqrt{5})$

إجابة: −4

مثال$\PageIndex{46}$

قم بالتبسيط:$(5−2\sqrt{3})(5+2\sqrt{3})$

إجابة

	$.$
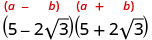
اضرب باستخدام نمط المربع ذي الحدين.	$.$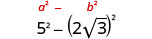
قم بالتبسيط.	$.$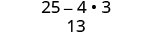

مثال$\PageIndex{47}$

قم بالتبسيط:$(3−2\sqrt{5})(3+2\sqrt{5})$.

إجابة: −11

مثال$\PageIndex{48}$

قم بالتبسيط:$(4+5\sqrt{7})(4−5\sqrt{7})$.

إجابة: −159

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية بضرب الجذور التربيعية.

خاصية المنتج
ضرب المعادلات ذات الحدين ذات الجذور التربيعية

المفاهيم الرئيسية

خاصية المنتج للجذور التربيعية إذا كانت a و b أرقامًا حقيقية غير سالبة، إذن
$\sqrt{ab}=\sqrt{a·b}$و$\sqrt{a}·\sqrt{b}=\sqrt{ab}$
صيغ خاصة لضرب المقادير ذات الحدين والمقترفات:
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
يمكن استخدام طريقة FOIL لمضاعفة الحدين المحتوية على الجذور.

	\((6\sqrt{2})(3\sqrt{10})\)
اضرب باستخدام خاصية المنتج.	\(18\sqrt{20}\)
قم بتبسيط الراديكالية.	\(18\sqrt{4}·\sqrt{5}\)
قم بالتبسيط.	\(18·2·\sqrt{5}\)
	\(36\sqrt{5}\)

	\((10\sqrt{6p^3})(3\sqrt{18p})\)
اضرب.	\(30\sqrt{108p^4}\)
قم بتبسيط الراديكالية.	\(30\sqrt{36p^4}·\sqrt{3}\)
	\(30·6p^2·\sqrt{3}\)
	\(180p^2\sqrt{3}\)

1.	\(\sqrt{5}(7+2\sqrt{5})\)
قم بالتوزيع.	\(7\sqrt{5}+2·5\)
قم بالتبسيط.	\(7\sqrt{5}+10\)
	\(10+7\sqrt{5}\)
2.	\(\sqrt{6}(\sqrt{2}+\sqrt{18})\)
اضرب.	\(\sqrt{12}+\sqrt{108}\)
قم بالتبسيط.	\((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\)
	\(2\sqrt{3}+6\sqrt{3}\)
اجمع مثل الراديكاليين.	\(8\sqrt{3}\)

	\((2+\sqrt{3})(4−\sqrt{3})\)
اضرب.	\(8−2\sqrt{3}+4\sqrt{3}−3\)
اجمع بين المصطلحات المتشابهة.	\(5+2\sqrt{3}\)

	\((3−2\sqrt{7})(4−2\sqrt{7})\)
اضرب.	\(12−6\sqrt{7}−8\sqrt{7}+4·7\)
قم بالتبسيط.	\(12−6\sqrt{7}−8\sqrt{7}+28\)
اجمع بين المصطلحات المتشابهة.	\(40−14\sqrt{7}\)

1.	\(\sqrt{2}·\sqrt{6}\)
اضرب باستخدام خاصية المنتج.	\(\sqrt{12}\)
قم بتبسيط الراديكالية.	\(\sqrt{4}·\sqrt{3}\)
قم بالتبسيط.	\(2\sqrt{3}\)
2.	\((4\sqrt{3})(2\sqrt{12})\)
اضرب باستخدام خاصية المنتج.	\(8\sqrt{36}\)
قم بتبسيط الراديكالية.	\(8·6\)
قم بالتبسيط.	\(48\)

1.	\((\sqrt{8x^3})(\sqrt{3x})\)
اضرب باستخدام خاصية المنتج.	\(\sqrt{24x^4}\)
قم بتبسيط الراديكالية.	\(\sqrt{4x^4}·\sqrt{6}\)
قم بالتبسيط.	\(2x^2\sqrt{6}\)
2.	\((\sqrt{20y^2})(\sqrt{5y^3})\)
اضرب باستخدام خاصية المنتج.	\(\sqrt{100y^5}\)
قم بتبسيط الراديكالية.	\(10y^2\sqrt{y}\)

1.	\((\sqrt{2})^2\)
أعد الكتابة كمنتج.	\((\sqrt{2})(\sqrt{2})\)
اضرب.	\(\sqrt{4}\)
قم بالتبسيط.	2
2.	\((−\sqrt{11})^2\)
أعد الكتابة كمنتج.	\((−\sqrt{11})(−\sqrt{11})\)
اضرب.	\(\sqrt{121}\)
قم بالتبسيط.	11

1.	\((2\sqrt{3})(8\sqrt{3})\)
اضرب. تذكر،\((\sqrt{3}^2)\)	16·3
قم بالتبسيط.	48
2.	\((3\sqrt{6})^2\)
اضرب.	9·6
قم بالتبسيط.	54

1.	\(3(5−\sqrt{2})\)
توزيع.	\(15−3\sqrt{2})\)
2.	\(\sqrt{2}(4−\sqrt{10})\)
توزيع.	\(4\sqrt{2}−\sqrt{20}\)
قم بالتبسيط.	\(4\sqrt{2}−2\sqrt{5}\)

	\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\)
اضرب.	\(3·2+12\sqrt{10}−\sqrt{10}−4·5\)
قم بالتبسيط.	\(6+12\sqrt{10}−\sqrt{10}−20\)
اجمع بين المصطلحات المتشابهة.	\(−14+11\sqrt{10}\)

	\((4−2\sqrt{x})(1+3\sqrt{x})\).
اضرب.	\(4+12\sqrt{x}−2\sqrt{x}−6x\)
اجمع بين المصطلحات المتشابهة.	\(4+10\sqrt{x}−6x\)

أهداف التعلم

ملاحظة

اضرب الجذور المربعة

تعريف: خاصية المنتج للجذور المربعة

مثال\(\PageIndex{1}\)

مثال\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

مثال\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

مثال\(\PageIndex{10}\)

مثال\(\PageIndex{11}\)

مثال\(\PageIndex{12}\)

مثال\(\PageIndex{13}\)

مثال\(\PageIndex{14}\)

مثال\(\PageIndex{15}\)

تعريف: تربيع الجذر التربيعي

مثال\(\PageIndex{16}\)

مثال\(\PageIndex{17}\)

مثال\(\PageIndex{18}\)

استخدم الضرب متعدد الحدود لضرب الجذور التربيعية

مثال\(\PageIndex{19}\)

مثال\(\PageIndex{20}\)

مثال\(\PageIndex{21}\)

مثال\(\PageIndex{22}\)

مثال\(\PageIndex{23}\)

مثال\(\PageIndex{24}\)

مثال\(\PageIndex{25}\)

مثال\(\PageIndex{26}\)

مثال\(\PageIndex{27}\)

مثال\(\PageIndex{28}\)

مثال\(\PageIndex{29}\)

مثال\(\PageIndex{30}\)

مثال\(\PageIndex{31}\)

مثال\(\PageIndex{32}\)

مثال\(\PageIndex{33}\)

مثال\(\PageIndex{34}\)

مثال\(\PageIndex{35}\)

مثال\(\PageIndex{36}\)

التعريف: صيغ المنتجات الخاصة

مثال\(\PageIndex{37}\)

مثال\(\PageIndex{38}\)

التمارين الرياضية\(\PageIndex{39}\)

مثال\(\PageIndex{40}\)

مثال\(\PageIndex{41}\)

مثال\(\PageIndex{42}\)

مثال\(\PageIndex{43}\)

مثال\(\PageIndex{44}\)

مثال\(\PageIndex{45}\)

مثال\(\PageIndex{46}\)

مثال\(\PageIndex{47}\)

مثال\(\PageIndex{48}\)

المفاهيم الرئيسية