9.2E: تمارين
- Page ID
- 200110
الممارسة تجعل من الكمال
استخدم خاصية المنتج لتبسيط الجذور المربعة
في التمارين التالية، قم بالتبسيط.
\(\sqrt{27}\)
- إجابة
-
\(3\sqrt{3}\)
\(\sqrt{80}\)
\(\sqrt{125}\)
- إجابة
-
\(5\sqrt{5}\)
\(\sqrt{96}\)
\(\sqrt{200}\)
- إجابة
-
\(10\sqrt{2}\)
\(\sqrt{147}\)
\(\sqrt{450}\)
- إجابة
-
\(15\sqrt{2}\)
\(\sqrt{252}\)
\(\sqrt{800}\)
- إجابة
-
\(20\sqrt{2}\)
\(\sqrt{288}\)
\(\sqrt{675}\)
- إجابة
-
\(15\sqrt{3}\)
\(\sqrt{1250}\)
\(\sqrt{x^7}\)
- إجابة
-
\(x^3\sqrt{x}\)
\(\sqrt{y^{11}}\)
\(\sqrt{p^3}\)
- إجابة
-
\(p\sqrt{p}\)
\(\sqrt{q^5}\)
\(\sqrt{m^{13}}\)
- إجابة
-
\(m^6\sqrt{m}\)
\(\sqrt{n^{21}}\)
\(\sqrt{r^{25}}\)
- إجابة
-
\(r^{12}\sqrt{r}\)
\(\sqrt{s^{33}}\)
\(\sqrt{49n^{17}}\)
- إجابة
-
\(7n^8\sqrt{n}\)
\(\sqrt{25m^9}\)
\(\sqrt{81r^{15}}\)
- إجابة
-
\(9r^7\sqrt{r}\)
\(\sqrt{100s^{19}}\)
\(\sqrt{98m^5}\)
- إجابة
-
\(7m^2\sqrt{2m}\)
\(\sqrt{32n^{11}}\)
\(\sqrt{125r^{13}}\)
- إجابة
-
\(5r^6\sqrt{5r}\)
\(\sqrt{80s^{15}}\)
\(\sqrt{200p^{13}}\)
- إجابة
-
\(10p^6\sqrt{2p}\)
\(\sqrt{128q^3}\)
\(\sqrt{242m^{23}}\)
- إجابة
-
\(11m^{11}\sqrt{2m}\)
\(\sqrt{175n^{13}}\)
\(\sqrt{147m^7n^{11}}\)
- إجابة
-
\(7m^3n^5\sqrt{3mn}\)
\(\sqrt{48m^7n^5}\)
\(\sqrt{75r^{13}s^{9}}\)
- إجابة
-
\(5r^{6}s^{4}\sqrt{3rs}\)
\(\sqrt{96r^3s^3}\)
\(\sqrt{300p^9q^{11}}\)
- إجابة
-
\(10p^4q^5\sqrt{3pq}\)
\(\sqrt{192q^3r^7}\)
\(\sqrt{242m^{13}n^{21}}\)
- إجابة
-
\(11m^6n^{10}\sqrt{2mn}\)
\(\sqrt{150m^9n^3}\)
\(5+\sqrt{12}\)
- إجابة
-
\(5+2\sqrt{3}\)
\(8+\sqrt{96}\)
\(1+\sqrt{45}\)
- إجابة
-
\(1+3\sqrt{5}\)
\(3+\sqrt{125}\)
\(\frac{10−\sqrt{24}}{2}\)
- إجابة
-
\(5−\sqrt{6}\)
\(\frac{8−\sqrt{80}}{4}\)
\(\frac{3+\sqrt{90}}{3}\)
- إجابة
-
\(1+\sqrt{10}\)
\(\frac{15+\sqrt{75}}{5}\)
استخدم خاصية حاصل القسمة لتبسيط الجذور التربيعية
في التمارين التالية، قم بالتبسيط.
\(\sqrt{\frac{49}{64}}\)
- إجابة
-
\(\frac{7}{8}\)
\(\sqrt{\frac{100}{36}}\)
\(\sqrt{\frac{121}{16}}\)
- إجابة
-
\(\frac{11}{4}\)
\(\sqrt{\frac{144}{169}}\)
\(\sqrt{\frac{72}{98}}\)
- إجابة
-
\(\frac{6}{7}\)
\(\sqrt{\frac{75}{12}}\)
\(\sqrt{\frac{45}{125}}\)
- إجابة
-
\(\frac{3}{5}\)
\(\sqrt{\frac{300}{243}}\)
\(\sqrt{\frac{x^{10}}{x^6}}\)
- إجابة
-
\(x^2\)
\(\sqrt{\frac{p^{20}}{p^{10}}}\)
\(\sqrt{\frac{y^4}{y^8}}\)
- إجابة
-
\(\frac{1}{y^2}\)
\(\sqrt{\frac{q^8}{q^{14}}}\)
\(\sqrt{\frac{200x^7}{2x^3}}\)
- إجابة
-
\(10x^2\)
\(\sqrt{\frac{98y^{11}}{2y^5}}\)
\(\sqrt{\frac{96p^9}{6p}}\)
- إجابة
-
\(4p^4\)
\(\sqrt{\frac{108q^{10}}{3q^2}}\)
\(\sqrt{\frac{36}{35}}\)
- إجابة
-
\(\frac{6}{\sqrt{35}}\)
\(\sqrt{\frac{144}{65}}\)
\(\sqrt{\frac{20}{81}}\)
- إجابة
-
\(\frac{2\sqrt{5}}{9}\)
\(\sqrt{\frac{211}{96}}\)
\(\sqrt{\frac{96x^7}{121}}\)
- إجابة
-
\(\frac{4x^3\sqrt{6x}}{11}\)
\(\sqrt{\frac{108y^4}{49}}\)
\(\sqrt{\frac{300m^5}{64}}\)
- إجابة
-
\(\frac{5m^2\sqrt{3m}}{4}\)
\(\sqrt{\frac{125n^7}{169}}\)
\(\sqrt{\frac{98r^5}{100}}\)
- إجابة
-
\(\frac{7r^2\sqrt{2r}}{10}\)
\(\sqrt{\frac{180s^{10}}{144}}\)
\(\sqrt{\frac{28q^6}{225}}\)
- إجابة
-
\(\frac{2q^3\sqrt{7}}{15}\)
\(\sqrt{\frac{150r^3}{256}}\)
\(\sqrt{\frac{75r^9}{s^8}}\)
- إجابة
-
\(\frac{5r^4\sqrt{3r}}{s^4}\)
\(\sqrt{\frac{72x^5}{y^6}}\)
\(\sqrt{\frac{28p^7}{q^2}}\)
- إجابة
-
\(\frac{4p^3\sqrt{7p}}{q}\)
\(\sqrt{\frac{45r^3}{s^{10}}}\)
\(\sqrt{\frac{100x^5}{36x^3}}\)
- إجابة
-
\(\frac{5x}{3}\)
\(\sqrt{\frac{49r^{12}}{16r^6}}\)
\(\sqrt{\frac{121p^5}{81p^2}}\)
- إجابة
-
\(\frac{11p\sqrt{p}}{9}\)
\(\sqrt{\frac{25r^8}{64r}}\)
\(\sqrt{\frac{32x^{5}y^{3}}{18x^{3}y}}\).
- إجابة
-
\(\frac{4xy}{3}\)
\(\sqrt{\frac{75r^{6}s^{8}}{48rs^{4}}}\)
\(\sqrt{\frac{27p^{2}q^{10}}{8p^5q^3}}\)
- إجابة
-
\(\frac{1}{2pq\sqrt{p}}\)
\(\sqrt{\frac{50r^5s^2}{128r^2s^5}}\)
الرياضيات اليومية
- قرر إليوت بناء حديقة مربعة تشغل 288 قدمًا مربعًا من فناء منزله. قم\(\sqrt{288}\) بالتبسيط لتحديد طول وعرض حديقته. قرِّب حتى أقرب عُشر قدم.
- لنفترض أن إليوت قرر تقليل حجم حديقته المربعة حتى يتمكن من إنشاء مسار مشي بعرض 5 أقدام على الجانبين الشمالي والشرقي للحديقة. قم\(\sqrt{288}−5\) بالتبسيط لتحديد طول وعرض الحديقة الجديدة. قرِّب حتى أقرب عُشر قدم.
- إجابة
-
- 17.0 قدم
- 15.0 قدم
- تسقط ميليسا بطريق الخطأ زوجًا من النظارات الشمسية من أعلى السفينة الدوارة، على ارتفاع 64 قدمًا فوق سطح الأرض. قم\(\sqrt{\frac{64}{16}}\) بالتبسيط لتحديد عدد الثواني التي تستغرقها النظارات الشمسية للوصول إلى الأرض.
- لنفترض أن النظارات الشمسية في المثال السابق قد سقطت من ارتفاع 144 قدمًا. قم\(\sqrt{\frac{144}{16}}\) بالتبسيط لتحديد عدد الثواني التي تستغرقها النظارات الشمسية للوصول إلى الأرض.
تمارين الكتابة
اشرح لماذا\(\sqrt{x^4}=x^2\). ثم اشرح لماذا\(\sqrt{x^{16}}=x^8\).
- إجابة
-
سوف تتنوع الإجابات.
اشرح لماذا لا\(7+\sqrt{9}\) يساوي\(\sqrt{7+9}\).
فحص ذاتي
ⓐ بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم إتقانك لأهداف هذا القسم.
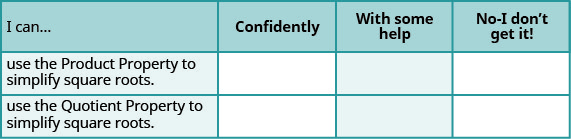
ⓑ بعد مراجعة قائمة التحقق هذه، ماذا ستفعل لتصبح واثقًا من جميع الأهداف؟


