Skip to main content
Global

8.9: استخدم التغيير المباشر والعكسي

  1. Last updated
  2. Save as PDF
  • Page ID
    200305

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • حل مشاكل الاختلاف المباشر
    • حل مسائل التباين العكسي
    ملاحظة

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    إذا فاتتك مشكلة، فارجع إلى القسم المدرج وراجع المادة.

    1. ابحث عن المعكوس الضربي للعدد −8
      إذا فاتتك هذه المشكلة، راجع التمرين 1.10.13.
    2. حل لـ n: 45=20n
      إذا فاتتك هذه المشكلة، راجع التمرين 2.2.1.
    3. قم بالتقييم\(5x^2\) عند x=10
      إذا فاتتك هذه المشكلة، راجع التمرين 1.3.25.

    عندما ترتبط كميتان بنسبة، نقول إنها تتناسب مع بعضها البعض. هناك طريقة أخرى للتعبير عن هذه العلاقة وهي التحدث عن اختلاف الكميتين. سنناقش الاختلاف المباشر والاختلاف العكسي في هذا القسم.

    حل مشاكل التباين المباشر

    تحصل ليندسي على أجر 15 دولارًا في الساعة في وظيفتها. إذا سمحنا لنا أن نكون راتبها وكان عدد الساعات التي عملت فيها، يمكننا أن نمثل هذا الموقف بالمعادلة

    s=15 ساعة

    راتب ليندسي هو نتاج ثابت، 15 ساعة، وعدد ساعات عملها. نقول أن راتب Lindsay يختلف بشكل مباشر مع عدد ساعات عملها. يختلف متغيران بشكل مباشر إذا كان أحدهما نتاج الثابت والآخر.

    التعريف: الاختلاف المباشر

    بالنسبة لأي متغيرين x و y، يختلف y بشكل مباشر مع x if

    y=kx، أين\(n \ne 0\)

    في التطبيقات التي تستخدم التباين المباشر، سنعرف عمومًا قيم زوج واحد من المتغيرات وسيُطلب منا إيجاد المعادلة التي تربط x و y. ثم يمكننا استخدام هذه المعادلة للعثور على قيم y لقيم x الأخرى.

    كيفية حل مشاكل التباين المباشر

    مثال\(\PageIndex{1}\)

    إذا كانت y تختلف بشكل مباشر مع x وy=20 عند x=8، فأوجد المعادلة التي تربط بين x وy.

    إجابة

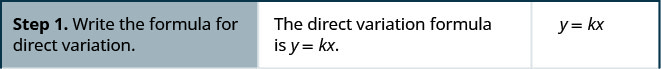
    تحتوي الصورة أعلاه على 3 أعمدة. يوضح الجدول خطوات حل مشكلات التباين المباشر. الخطوة الأولى هي كتابة صيغة الاختلاف المباشر. صيغة التباين المباشر هي y تساوي k x. ثم نحصل على y يساوي k في x.الخطوة الثانية هي استبدال القيم المعطاة للمتغيرات. أُعطينا y يساوي 20 و x يساوي 8. ثم لدينا 20 يساوي k في 8.الخطوة الثالثة هي حل الاختلاف المستمر. اقسم طرفي المعادلة على 8، ثم اضرب. نحصل الآن على 20 مقسومًا على 8 يساوي k. K يساوي 2.5.الخطوة الرابعة هي كتابة المعادلة التي تربط x و y. أعد كتابة المعادلة العامة بالقيمة التي وجدناها k للحصول على y يساوي 2 وخمسة أعشار في x.

    مثال\(\PageIndex{2}\)

    إذا كانت y تتغير بشكل مباشر كـ x وy=3، عندما تكون x=10، فأوجد المعادلة التي تربط بين x وy.

    إجابة

    \(y=\frac{3}{10}x\)

    مثال\(\PageIndex{3}\)

    إذا تغيّرت y بشكل مباشر كـ x وy=12 عند x=4، فأوجد المعادلة التي تربط بين x وy.

    إجابة

    ص = 3 ×

    سنقوم بإدراج الخطوات أدناه.

    التعريف: حل مشاكل التباين المباشر
    1. اكتب صيغة التغيُّر المباشر.
    2. استبدل القيم المعطاة بالمتغيرات.
    3. حل لثابت الاختلاف.
    4. اكتب المعادلة التي تربط بين x وy.

    الآن سنحل بعض تطبيقات الاختلاف المباشر.

    مثال\(\PageIndex{4}\)

    عندما يركض راؤول على جهاز المشي في صالة الألعاب الرياضية، يختلف عدد السعرات الحرارية، c، التي يحرقها بشكل مباشر مع عدد الدقائق، m، يستخدم جهاز المشي. لقد أحرق 315 سعرة حرارية عندما استخدم جهاز الجري لمدة 18 دقيقة.

    1. اكتب المعادلة التي تربط c وm.
    2. كم عدد السعرات الحرارية التي سيحرقها إذا ركض على جهاز المشي لمدة 25 دقيقة؟
    إجابة

    1.

      يختلف عدد السعرات الحرارية، c بشكل مباشر مع عدد الدقائق، m، على جهاز المشي، و c=315 عندما m=18
    اكتب صيغة التغيُّر المباشر. .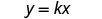
    سوف نستخدم c بدلاً من y و mm بدلاً من x. .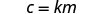
    استبدل القيم المعطاة بالمتغيرات. .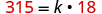
    حل لثابت الاختلاف. .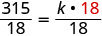
      .
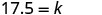
    اكتب المعادلة التي تربط c وm. .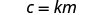
    استبدل في ثابت الاختلاف. .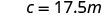

    2.

     

    ابحث عن c عندما m=25.
    اكتب المعادلة التي تربط c وm. .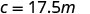
    استبدل القيمة المعطاة بـ m. .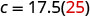
    قم بالتبسيط. .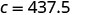
      سيحرق راؤول 437.5 سعرة حرارية إذا استخدم جهاز الجري لمدة 25 دقيقة.
    مثال\(\PageIndex{5}\)

    يختلف عدد السعرات الحرارية المحروقة بشكل مباشر مع مقدار الوقت المستغرق في ممارسة الرياضة. أحرق أرنولد 312 سعرة حرارية في 65 دقيقة من التمارين.

    1. اكتب المعادلة التي تربط c وt.
    2. كم عدد السعرات الحرارية التي سيحرقها إذا مارس الرياضة لمدة 90 دقيقة؟
    إجابة
    1. c=4.8t
    2. 432 سعرة حرارية
    مثال\(\PageIndex{6}\)

    تختلف المسافة التي يقطعها الجسم المتحرك، d، بشكل مباشر مع الوقت، t، يتحرك. يسافر القطار 100 ميل في ساعتين

    1. اكتب المعادلة التي تربط d وt.
    2. كم عدد الأميال التي ستقطعها في 5 ساعات؟
    إجابة
    1. د = 50 طن
    2. 250 ميلاً

    في المثال السابق، تم تسمية المتغيرات c و m في المشكلة. عادة ليس هذا هو الحال. سيتعين علينا تسمية المتغيرات في المثال التالي كجزء من الحل، تمامًا كما نفعل في معظم المشكلات التطبيقية.

    مثال\(\PageIndex{7}\)

    يختلف عدد غالونات الغاز التي تستخدمها سيارة Eunice بشكل مباشر مع عدد الأميال التي تقطعها. في الأسبوع الماضي، سافرت 469.8 ميلاً واستخدمت 14.5 جالونًا من الغاز.

    1. اكتب المعادلة التي تربط عدد جالونات الغاز المستخدمة بعدد الأميال المقطوعة.
    2. كم عدد غالونات الغاز التي ستستخدمها سيارة يونيس إذا قطعت مسافة 1000 ميل؟
    إجابة

    1.

      يختلف عدد جالونات الغاز بشكل مباشر مع عدد الأميال المقطوعة.
    أولاً سنقوم بتسمية المتغيرات. دعونا g = عدد جالونات الغاز.
    m= عدد الأميال المقطوعة.
    اكتب صيغة التغيُّر المباشر. .
    سنستخدم g بدلاً من y و m بدلاً من x. .
    استبدل القيم المعطاة للمتغيرات .
      .
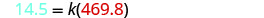
    حل لثابت الاختلاف. .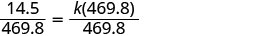
    سنصل إلى أقرب جزء من ألف. .
    اكتب المعادلة التي تربط g وm. .
    استبدل في ثابت الاختلاف. .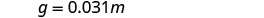

    2.

      ابحث عن g عندما m=1000.
    اكتب المعادلة التي تربط g وm. ز = 0.0331 متر
    استبدل القيمة المعطاة بـ m. g = 0.031 (1000)
    قم بالتبسيط. ز = 31
      ستستخدم سيارة يونيس 31 جالونًا من الغاز إذا قادتها لمسافة 1000 ميل.

    لاحظ أنه في هذا المثال، الوحدات على ثابت التباين هي جالون/ميل. في الحياة اليومية، نتحدث عادة عن أميال/جالون.

    مثال\(\PageIndex{8}\)

    تختلف المسافة التي يقطعها براد بشكل مباشر مع الوقت الذي يقضيه في السفر. سافر براد 660 ميلاً في 12 ساعة

    1. اكتب المعادلة التي تربط عدد الأميال المقطوعة بالوقت.
    2. كم عدد الأميال التي يمكن أن يقطعها براد في 4 ساعات؟
    إجابة
    1. م = 55 ساعة
    2. 220 ميلاً
    مثال\(\PageIndex{9}\)

    يختلف وزن السائل بشكل مباشر حسب حجمه. يبلغ حجم السائل الذي يزن 24 رطلاً 4 جالونات.

    1. اكتب المعادلة التي تربط الوزن بالحجم.
    2. إذا كان حجم السائل ١٣ جالونًا، فما وزنه؟
    إجابة
    1. ث = 6 فولت
    2. 78 رطلاً

    في بعض الحالات، يختلف متغير واحد بشكل مباشر مع مربع المتغير الآخر. عندما يحدث ذلك، تكون معادلة التباين المباشر هي\(y=kx^2\).

    مثال\(\PageIndex{10}\)

    يختلف الحد الأقصى للحمل الذي ستدعمه الحزمة بشكل مباشر مع مربع قطر المقطع العرضي للشعاع. شعاع بقطر 4 بوصة سيدعم حمولة قصوى تبلغ 75 رطلاً.

    1. اكتب المعادلة التي تربط الحمل الأقصى بالمقطع العرضي.
    2. ما الحد الأقصى للحمل الذي يمكن دعمه بواسطة شعاع بقطر 8 بوصة؟
    إجابة

    1.

      يختلف الحد الأقصى للحمل بشكل مباشر مع مربع قطر المقطع العرضي.
    قم بتسمية المتغيرات. دع L = الحد الأقصى للحمل.
    c = قطر المقطع العرضي
    اكتب صيغة التغيُّر المباشر، حيث يتغيَّر y بشكل مباشر مع مربع x. .
    سوف نستخدم L بدلاً من y و c بدلاً من x. .
    استبدل القيم المعطاة بالمتغيرات. .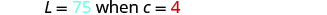
      .
    حل لثابت الاختلاف. .
      .
    اكتب المعادلة التي تربط بين L و c. .
    استبدل في ثابت الاختلاف. .

    2.

      ابحث عن L عندما c=8.
    اكتب المعادلة التي تربط بين L و c. \(L=4.6875c^2\)
    استبدل القيمة المعطاة بـ c. \(L=4.6875(8)^2\)
    قم بالتبسيط. لتر=300
      يمكن لشعاع بقطر 8 بوصة أن يدعم حمولة قصوى تبلغ 300 رطل.
    مثال\(\PageIndex{11}\)

    المسافة التي يسقطها الجسم تتناسب طرديًا مع مربع الوقت الذي يسقط فيه. تسقط كرة 144 قدمًا في ٣ ثوانٍ.

    1. اكتب المعادلة التي تربط المسافة بالوقت.
    2. إلى أي مدى سيسقط جسم في 4 ثوانٍ؟
    إجابة
    1. \(d=16t^2\)
    2. 256 قدمًا
    مثال\(\PageIndex{12}\)

    تختلف مساحة الدائرة بشكل مباشر كمربع نصف القطر. تبلغ مساحة البيتزا الدائرية التي يبلغ قطرها 6 بوصات 113.04 بوصة مربعة.

    1. اكتب المعادلة التي تربط المنطقة بنصف القطر.
    2. ما مساحة البيتزا التي يبلغ نصف قطرها ٩ بوصات؟
    إجابة
    1. \(A=3.14r^2\)
    2. 254.34 بوصة مربعة

    حل مسائل التباين العكسي

    تتضمن العديد من التطبيقات متغيرين يختلفان عكسيًا. كلما زاد أحد المتغيرات، ينخفض الآخر. المعادلة التي تربطهم هي\(y=\frac{k}{x}\).

    تعريف: الاختلاف العكسي

    بالنسبة لأي متغيرين x و y، يختلف y عكسيًا مع x if

    y =\(\frac{k}{x}\)، أين\(k \ne 0\)

    تشير كلمة «معكوس» في التباين العكسي إلى المعكوس الضربي. المعكوس الضربي لـ x هو\(\frac{1}{x}\).

    نحن نحل مشاكل التباين العكسي بنفس الطريقة التي حللنا بها مشاكل التباين المباشر. تم تغيير الشكل العام للمعادلة فقط. سنقوم بنسخ مربع الإجراءات هنا وتغيير كلمة «مباشر» إلى «عكسي».

    التعريف: حل مشاكل التباين العكسي
    1. اكتب صيغة التغيُّر العكسي.
    2. استبدل القيم المعطاة بالمتغيرات.
    3. حل لثابت الاختلاف.
    4. اكتب المعادلة التي تربط بين x وy.
    مثال\(\PageIndex{13}\)

    إذا كان y يختلف عكسيًا مع x و y = 20 عندما x = 8 x و y.

    إجابة
    اكتب صيغة التغيُّر العكسي. .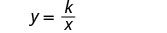
    استبدل القيم المعطاة بالمتغيرات. .
      .
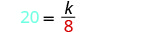
    حل لثابت الاختلاف. .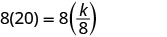
      .
    اكتب المعادلة التي تربط بين x وy. .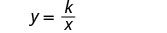
    استبدل في ثابت الاختلاف. .
    مثال\(\PageIndex{14}\)

    إذا تغيرت p عكسيًا بـ q و p=30 عندما q=12، فأوجد المعادلة التي تربط p و q.

    إجابة

    \(p=\frac{360}{q}\)

    مثال\(\PageIndex{15}\)

    إذا كان y يتغير عكسيًا مع x و y=8 عندما x=2 ابحث عن المعادلة التي تربط x و y.

    إجابة

    \(y=\frac{16}{x}\)

    مثال\(\PageIndex{16}\)

    يختلف استهلاك الوقود (mpg) للسيارة بشكل عكسي مع وزنها. السيارة التي تزن 3100 رطل تحصل على 26 ميلا في الغالون على الطريق السريع.

    1. اكتب معادلة الاختلاف.
    2. ماذا سيكون استهلاك الوقود لسيارة تزن 4030 رطلاً؟
    إجابة

    1.

      يختلف استهلاك الوقود عكسيًا مع الوزن.
    أولاً سنقوم بتسمية المتغيرات. دع f = استهلاك الوقود.
    w = الوزن.
    اكتب صيغة التغيُّر العكسي. .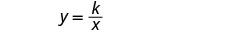
    سنستخدم f بدلاً من y و w بدلاً من x. .
    استبدل القيم المعطاة بالمتغيرات. .
      .
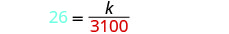
    حل لثابت الاختلاف. .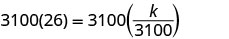
      .
    اكتب المعادلة التي تربط بين f و w. .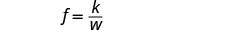
    استبدل في ثابت الاختلاف. .

    2.

      ابحث عن متى w=4030.
    اكتب المعادلة التي تربط بين f و w. .
    استبدل القيمة المعطاة بـ w. \(f=\frac{80,600}{4030}\)
    قم بالتبسيط. f = 20
      السيارة التي تزن 40-30 رطلاً سيكون استهلاكها للوقود 20 ميلا في الغالون.
    مثال\(\PageIndex{17}\)

    تختلف قيمة السيارة عكسيًا مع عمرها. اشترت إيلينا سيارة عمرها عامين مقابل 20,000 دولار.

    1. اكتب معادلة الاختلاف.
    2. ماذا ستكون قيمة سيارة إيلينا عندما تبلغ من العمر 5 سنوات؟
    إجابة
    1. \(v=\frac{40,000}{a}\)
    2. 8,000 دولار
    مثال\(\PageIndex{18}\)

    يختلف الوقت المطلوب لتفريغ حوض السباحة عكسيًا مثل معدل الضخ. استغرقت لوسي 2.5 ساعة لتفريغ حمام السباحة الخاص بها باستخدام مضخة تم تصنيفها بـ 400 gpm (جالون في الدقيقة).

    1. اكتب معادلة الاختلاف.
    2. كم من الوقت ستستغرق لتفريغ حوض السباحة باستخدام مضخة بمعدل 500 جالون في الدقيقة؟
    إجابة
    1. \(t=\frac{1000}{r}\)
    2. 2 ساعة
    مثال\(\PageIndex{19}\)

    يختلف تردد سلسلة الجيتار عكسيًا مع طولها. يبلغ تردد سلسلة طولها 26 بوصة 440 اهتزازًا في الثانية.

    1. اكتب معادلة الاختلاف.
    2. كم عدد الاهتزازات في الثانية إذا تم تقليل طول الخيط إلى 20 بوصة عن طريق وضع إصبع على الحنق؟
    إجابة

    1.

      يختلف التردد عكسيًا مع الطول.
    قم بتسمية المتغيرات. دع f = التردد.
    L = الطول.
    اكتب صيغة التغيُّر العكسي. .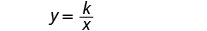
    سنستخدم f بدلاً من y و L بدلاً من x .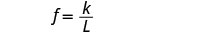
    استبدل القيم المعطاة بالمتغيرات. .
      .
    حل لثابت الاختلاف. .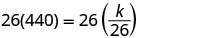
      .
    اكتب المعادلة التي تربط f وL. .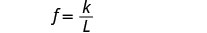
    استبدل في ثابت الاختلاف. .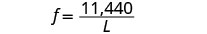

    2.

      ابحث عن متى L = 20.
    اكتب المعادلة التي تربط f وL. \(f=\frac{11,440}{L}\)
    استبدل القيمة المعطاة بـ L. \(f=\frac{11,440}{20}\)
    قم بالتبسيط. f=572
      تردد سلسلة الجيتار مقاس 20 بوصة 572 اهتزازًا في الثانية.
    مثال\(\PageIndex{20}\)

    يختلف عدد الساعات التي يستغرقها ذوبان الثلج عكسيًا مع درجة حرارة الهواء. لنفترض أن كتلة من الجليد تذوب في ساعتين عندما تكون درجة الحرارة 65 درجة.

    1. اكتب معادلة الاختلاف.
    2. ما عدد الساعات التي سيستغرقها ذوبان الكتلة الجليدية نفسها إذا كانت درجة الحرارة 78 درجة؟
    إجابة
    1. \(h=\frac{130}{t}\)
    2. \(1\frac{2}{3}\)ساعات
    مثال\(\PageIndex{21}\)

    تختلف القوة اللازمة لكسر اللوح عكسيًا مع طوله. يستخدم ريتشارد 24 رطلاً من الضغط لكسر لوح طوله 2 قدم.

    1. اكتب معادلة الاختلاف.
    2. ما عدد الأرطال من الضغط اللازم لكسر لوح طوله 5 أقدام؟
    إجابة
    1. \(F=\frac{48}{L}\)
    2. 9.6 رطل