8.6: حل المعادلات الكسرية
- Page ID
- 200317
في نهاية هذا القسم، ستكون قادرًا على:
- حل المعادلات العقلانية
- حل معادلة عقلانية لمتغير معين
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
إذا فاتتك مشكلة، فارجع إلى القسم المدرج وراجع المادة.
- حل:\(\frac{1}{6}x+\frac{1}{2}=\frac{1}{3}\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.5.1. - حل:\(n^2−5n−36=0\).
إذا فاتتك هذه المشكلة، راجع التمرين 7.6.13. - حل لـ y بدلالة x: 5x+2y=10 لـ y.
إذا فاتتك هذه المشكلة، راجع التمرين 2.6.22.
بعد تحديد مصطلحي التعبير والمعادلة في وقت مبكر من كتاب التأسيس، استخدمناهما في جميع أنحاء هذا الكتاب. لقد قمنا بتبسيط العديد من أنواع التعبيرات وحل العديد من أنواع المعادلات. لقد قمنا بتبسيط العديد من التعبيرات العقلانية حتى الآن في هذا الفصل. الآن سنحل المعادلات العقلانية.
يشبه تعريف المعادلة العقلانية تعريف المعادلة الذي استخدمناه في التأسيس.
المعادلة الكسرية هي تعبيرين كسريين متصلين بعلامة تساوي.
يجب عليك التأكد من معرفة الفرق بين التعبيرات العقلانية والمعادلات العقلانية. تحتوي المعادلة على علامة المساواة.
\[\begin{array}{cc} {\textbf{Rational Expression}}&{\textbf{Rational Equation}}\\ {\frac{1}{8}x+\frac{1}{2}}&{\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}}\\ {\frac{y+6}{y^2−36}}&{\frac{y+6}{y^2−36}=y+1}\\ {\frac{1}{n−3}+\frac{1}{n+4}}&{\frac{1}{n−3}+\frac{1}{n+4}=\frac{15}{n^2+n−12}}\\ \nonumber \end{array}\]
حل المعادلات الكسرية
لقد قمنا بالفعل بحل المعادلات الخطية التي تحتوي على كسور. وجدنا شاشة LCD لجميع الكسور في المعادلة ثم ضربنا جانبي المعادلة في شاشة LCD «لمسح» الكسور.
في ما يلي مثال قمنا به عندما عملنا مع المعادلات الخطية:
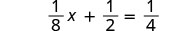 |
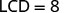 |
|
| قمنا بضرب كلا الجانبين بواسطة شاشة LCD. | 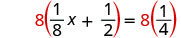 |
|
| ثم قمنا بالتوزيع. | 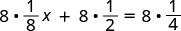 |
|
| قمنا بالتبسيط - ثم حصلنا على معادلة بدون كسور. | 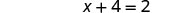 |
|
| أخيرًا، قمنا بحل هذه المعادلة. | 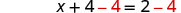 |
|
 |
سنستخدم نفس الإستراتيجية لحل المعادلات العقلانية. سنضرب كلا جانبي المعادلة في شاشة LCD. ثم سيكون لدينا معادلة لا تحتوي على تعبيرات عقلانية وبالتالي يسهل علينا حلها.
ولكن نظرًا لأن المعادلة الأصلية قد تحتوي على متغير في المقام، يجب أن نكون حذرين حتى لا ننتهي بحل يجعل القاسم يساوي صفرًا.
لذا قبل أن نبدأ في حل المعادلة النسبية، نفحصها أولاً لإيجاد القيم التي تجعل أي مقامات صفرًا. بهذه الطريقة، عندما نحل معادلة عقلانية، سنعرف ما إذا كانت هناك أي حلول جبرية يجب علينا تجاهلها.
الحل الجبري للمعادلة العقلانية التي من شأنها أن تتسبب في عدم تعريف أي من التعبيرات العقلانية يسمى الحل الخارجي.
الحل الخارجي للمعادلة العقلانية هو الحل الجبري الذي من شأنه أن يتسبب في عدم تعريف أي من التعبيرات في المعادلة الأصلية.
نلاحظ أي حلول خارجية ممكنة، ج، عن طريق الكتابة\(x \ne c\) next to the equation.
كيفية حل المعادلات باستخدام التعبيرات النسبية
حل:\(\frac{1}{x}+\frac{1}{3}=\frac{5}{6}\).
- إجابة
-

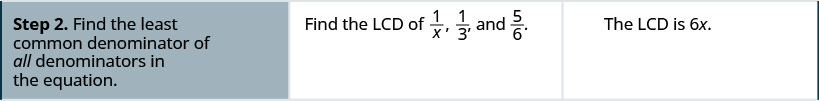



حل:\(\frac{1}{y}+\frac{2}{3}=\frac{1}{5}\).
- إجابة
-
\(−\frac{15}{7}\)
حل:\(\frac{2}{3}+\frac{1}{5}=\frac{1}{x}\).
- إجابة
-
\(\frac{15}{13}\)
يتم عرض خطوات هذه الطريقة أدناه.
- لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا.
- أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة.
- امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD.
- حل المعادلة الناتجة.
- تحقق.
- إذا كانت أي قيم موجودة في الخطوة 1 عبارة عن حلول جبرية، فتجاهلها.
- تحقق من أي حلول متبقية في المعادلة الأصلية.
نبدأ دائمًا بملاحظة القيم التي قد تتسبب في أن تكون أي مقامات صفرًا.
حل:\(1−\frac{5}{y}=−\frac{6}{y^2}\).
- إجابة
-
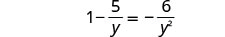
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 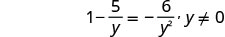
أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة. شاشة ال سي دي هي\(y^2\) امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD. 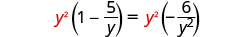
قم بالتوزيع. 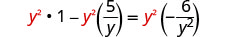
اضرب. 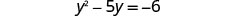
حل المعادلة الناتجة. اكتب أولاً المعادلة التربيعية في الصورة القياسية. 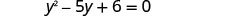
عامل. 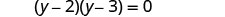
استخدم خاصية المنتج الصفري. 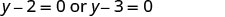
حل. 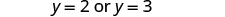
تحقق. لم نحصل على 0 كحل جبري. 
حل:\(1−\frac{2}{a}=\frac{15}{a^2}\).
- إجابة
-
5، −3
حل:\(1−\frac{4}{b}=\frac{12}{b^2}\).
- إجابة
-
6، −2
حل:\(\frac{5}{3u−2}=\frac{3}{2u}\).
- إجابة
-
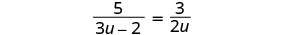
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 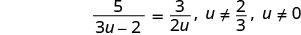
أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة. شاشة ال سي دي هي 2u (3u−2). امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD. 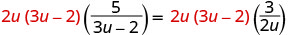
قم بإزالة العوامل المشتركة. 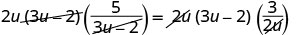
قم بالتبسيط. 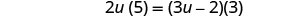
اضرب. 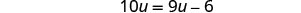
حل المعادلة الناتجة. 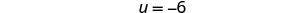
لم نحصل على 0 أو\(\frac{2}{3}\) كحلول جبرية. 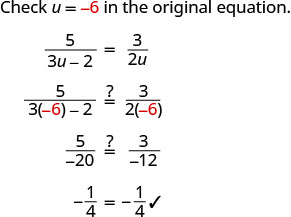
حل:\(\frac{1}{x−1}=\frac{2}{3x}\).
- إجابة
-
−2
حل:\(\frac{3}{5n+1}=\frac{2}{3n}\).
- إجابة
-
−2
عندما تكون إحدى المقامات تربيعية، تذكر أخذها في الاعتبار أولاً للعثور على شاشة LCD.
حل:\(\frac{2}{p+2}+\frac{4}{p−2}=\frac{p−1}{p^2−4}\).
- إجابة
-
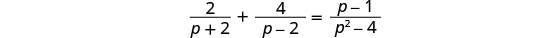
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 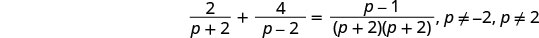
أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة. شاشة LCD هي (p+2) (p−2). امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD. 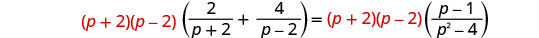
قم بالتوزيع. 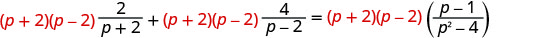
قم بإزالة العوامل المشتركة. 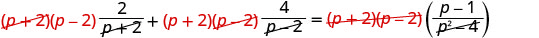
قم بالتبسيط. 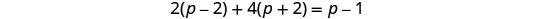
قم بالتوزيع. 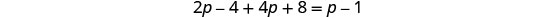
حل. 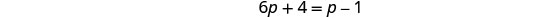


لم نحصل على 2 أو −2 كحلول جبرية. 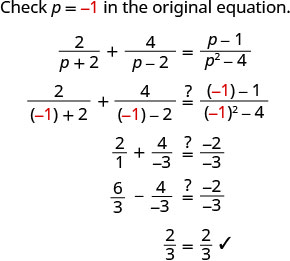
حل:\(\frac{2}{x+1}+\frac{1}{x−1}=\frac{1}{x^2−1}\).
- إجابة
-
\(\frac{2}{3}\)
حل:\(\frac{5}{y+3}+\frac{2}{y−3}=\frac{5}{y^2−9}\)
- إجابة
-
2
حل:\(\frac{4}{q−4}−\frac{3}{q−3}=1\).
- إجابة
-

لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 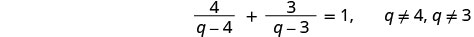
أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة. شاشة LCD هي (q−4) (q−3). امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD. 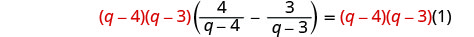
قم بالتوزيع. 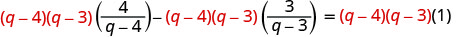
قم بإزالة العوامل المشتركة. 
قم بالتبسيط. 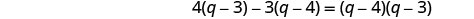
قم بالتبسيط. 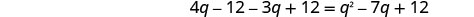
اجمع بين المصطلحات المتشابهة. 
حل. اكتب أولاً في النموذج القياسي. 
عامل. 
استخدم خاصية المنتج الصفري. 
لم نحصل على 4 أو 3 كحلول جبرية. 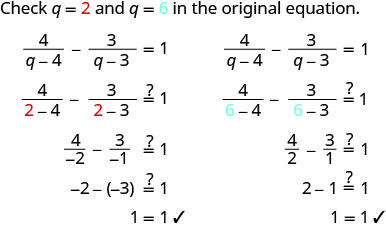
حل:\(\frac{2}{x+5}−\frac{1}{x−1}=1\).
- إجابة
-
−1، −2
حل:\(\frac{3}{x+8}−\frac{2}{x−2}=1\).
- إجابة
-
−2، −3
حل:\(\frac{m+11}{m^2−5m+4}=\frac{5}{m−4}−\frac{3}{m−1}\).
- إجابة
-
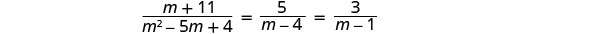
ضع في اعتبارك جميع القواسم، حتى نتمكن من ملاحظة أي قيمة للمتغير تجعل أي مقام صفرًا. 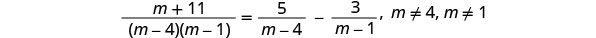
أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة. شاشة LCD هي (m−4) (m−1) امسح الكسور. 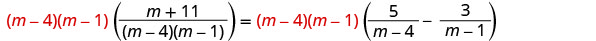
قم بالتوزيع. 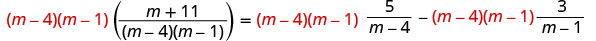
قم بإزالة العوامل المشتركة. 
قم بالتبسيط. 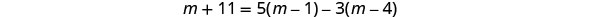
حل المعادلة الناتجة. 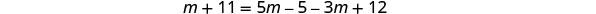

تحقق. كان الحل الجبري الوحيد هو 4، لكننا قلنا أن 4 سيجعل المقام يساوي صفرًا. الحل الجبري هو حل خارجي. لا يوجد حل لهذه المعادلة.
حل:\(\frac{x+13}{x^2−7x+10}=\frac{6}{x−5}−\frac{4}{x−2}\).
- إجابة
-
لا يوجد حل
حل:\(\frac{y−14}{y^2+3y−4}=\frac{2}{y+4}+\frac{7}{y−1}\).
- إجابة
-
لا يوجد حل
كانت المعادلة التي حللناها في المثال تحتوي على حل جبري واحد فقط، لكنها كانت حلًا غريبًا. لم يترك لنا ذلك أي حل للمعادلة. بعض المعادلات ليس لها حل.
حل:\(\frac{n}{12}+\frac{n+3}{3n}=\frac{1}{n}\).
- إجابة
-
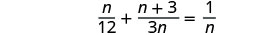
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 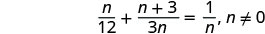
أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة. شاشة ال سي دي هي 12 بوصة. امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD. 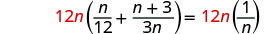
قم بالتوزيع. 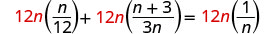
قم بإزالة العوامل المشتركة. 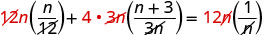
قم بالتبسيط. 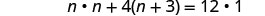
حل المعادلة الناتجة. 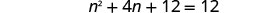
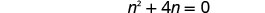
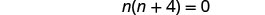
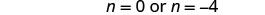
تحقق. n=0 هو حل خارجي. 
حل:\(\frac{x}{18}+\frac{x+6}{9x}=\frac{2}{3x}\).
- إجابة
-
−2
حل:\(\frac{y+5}{5y}+\frac{y}{15}=\frac{1}{y}\).
- إجابة
-
−3
حل:\(\frac{y}{y+6}=\frac{72}{y^2−36}+4\).
- إجابة
-
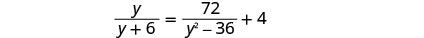
ضع في اعتبارك جميع القواسم، حتى نتمكن من ملاحظة أي قيمة للمتغير تجعل أي مقام صفرًا. 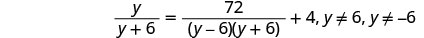
أوجد القاسم المشترك الأصغر. شاشة LCD هي (y−6) (y+6). امسح الكسور. 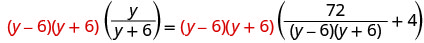
قم بالتبسيط. 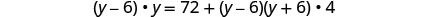
قم بالتبسيط. 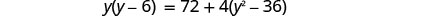
حل المعادلة الناتجة. 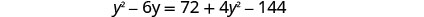
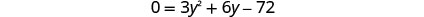
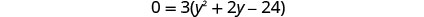
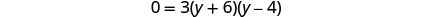
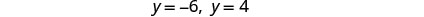
تحقق. y=−6 هو حل خارجي. 
حل:\(\frac{x}{x+4}=\frac{32}{x^2−16}+5\).
- إجابة
-
−4، 3
حل:\(\frac{y}{y+8}=\frac{128}{y^2−64}+9\).
- إجابة
-
7
حل:\(\frac{x}{2x−2}−\frac{2}{3x+3}=\frac{5x^2−2x+9}{12x^2−12}\).
- إجابة
-
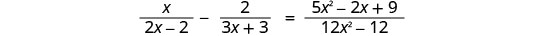
سنبدأ بتحليل جميع القواسم، لتسهيل تحديد الحلول الخارجية وشاشات الكريستال السائل. 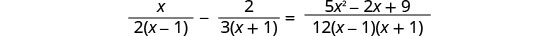
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 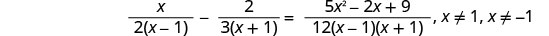
ابحث عن القاسم المشترك الأقل. شاشة LCD هي 12 (x−1) (x+1) امسح الكسور. 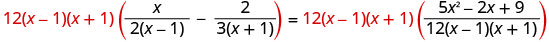
قم بالتبسيط. 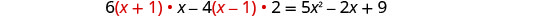
قم بالتبسيط. 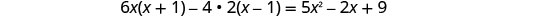
حل المعادلة الناتجة. 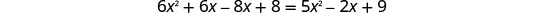
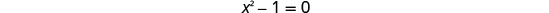
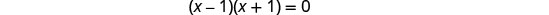
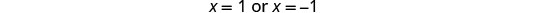
تحقق. x=1 و x=−1 هي حلول غريبة.
لا يوجد حل للمعادلة.
حل:\(\frac{y}{5y−10}−\frac{5}{3y+6}=\frac{2y^2−19y+54}{15y^2−60}\).
- إجابة
-
لا يوجد حل
حل:\(\frac{z^2}{z+8}−\frac{3}{4z−8}=\frac{3z^2−16z−68}{z^2+8z−64}\).
- إجابة
-
لا يوجد حل
حل معادلة نسبية لمتغير معين
عندما قمنا بحل المعادلات الخطية، تعلمنا كيفية حل صيغة لمتغير معين. تستخدم العديد من الصيغ المستخدمة في الأعمال والعلوم والاقتصاد والمجالات الأخرى المعادلات العقلانية لنمذجة العلاقة بين متغيرين أو أكثر. سنرى الآن كيفية حل معادلة عقلانية لمتغير معين.
سنبدأ بصيغة تتعلق بالمسافة والمعدل والوقت. لقد استخدمناها عدة مرات من قبل، ولكن ليس عادةً بهذا الشكل.
الحل: من\(\frac{D}{T}=R\) أجل T.
- إجابة
-
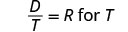
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 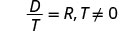
امسح الكسور بضرب كلا طرفي المعادلات في شاشة LCD، T. 
قم بالتبسيط. 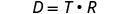
قسّم كلا الجانبين على R لعزل T. 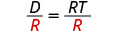
قم بالتبسيط. 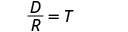
الحل:\(\frac{A}{L}=W\) لـ L.
- إجابة
-
\(L=\frac{A}{W}\)
حل: من\(\frac{F}{A}=M\) أجل A.
- إجابة
-
\(A=\frac{F}{M}\)
يستخدم المثال صيغة المنحدر التي استخدمناها للحصول على شكل نقطة المنحدر لمعادلة الخط المستقيم.
حل:\(m=\frac{x−2}{y−3}\) بالنسبة لي.
- إجابة
-
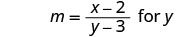
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 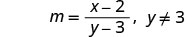
امسح الكسور بضرب كلا طرفي المعادلات في شاشة LCD، y−3. 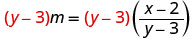
قم بالتبسيط. 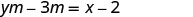
اعزل المصطلح بـ y. 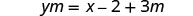
قسّم كلا الجانبين على m لعزل y. 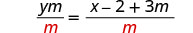
قم بالتبسيط. 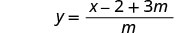
حل:\(\frac{y−2}{x+1}=\frac{2}{3}\) لـ x.
- إجابة
-
\(x=\frac{3y−8}{2}\)
حل:\(x=\frac{y}{1−y}\) بالنسبة لي.
- إجابة
-
\(y=\frac{x}{1+x}\)
تأكد من اتباع جميع الخطوات في المثال. قد تبدو وكأنها صيغة بسيطة للغاية، ولكن لا يمكننا حلها على الفور لأي من القاسمين.
حل\(\frac{1}{c}+\frac{1}{m}=1\) لـ ج.
- إجابة
-
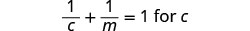
لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا. 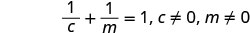
امسح الكسور بضرب كلا طرفي المعادلات في شاشة LCD، سم 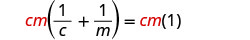
قم بالتوزيع. 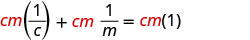
قم بالتبسيط. 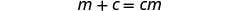
اجمع الشروط مع c على اليمين. 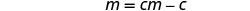
ضع في اعتبارك التعبير الموجود على اليمين. 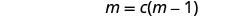
لعزل c، قسّم كلا الجانبين على m−1. 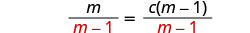
قم بالتبسيط من خلال إزالة العوامل المشتركة. 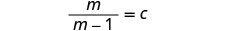
لاحظ أنه على الرغم من أننا استبعدنا c=0 و m=0 من المعادلة الأصلية، يجب علينا الآن أيضًا ذكر ذلك\(m \ne 1\).
حل:\(\frac{1}{a}+\frac{1}{b}=c\) للحصول على.
- إجابة
-
\(a=\frac{b}{cb−1}\)
حل:\(\frac{2}{x}+\frac{1}{3}=\frac{1}{y}\) بالنسبة لي.
- إجابة
-
\(y=\frac{3x}{6+x}\)
المفاهيم الرئيسية
- إستراتيجية حل المعادلات باستخدام التعبيرات النسبية
- لاحظ أي قيمة للمتغير من شأنها أن تجعل أي قاسم صفرًا.
- أوجد المقام المشترك الأصغر لجميع المقامات في المعادلة.
- امسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD.
- حل المعادلة الناتجة.
- تحقق.
- إذا كانت أي قيم موجودة في الخطوة 1 عبارة عن حلول جبرية، فتجاهلها.
- تحقق من أي حلول متبقية في المعادلة الأصلية.
مسرد المصطلحات
- معادلة عقلانية
- المعادلة الكسرية هي تعبيرين كسريين متصلين بعلامة تساوي.
- حل خارجي لمعادلة عقلانية
- الحل الخارجي للمعادلة العقلانية هو الحل الجبري الذي من شأنه أن يتسبب في عدم تعريف أي من التعبيرات في المعادلة الأصلية.


