8.5E: تمارين
- Page ID
- 200349
الممارسة تجعل من الكمال
بسِّط مقدارًا كسريًا معقدًا بكتابته في صورة قسمة
في التمارين التالية، قم بالتبسيط.
\(\frac{\frac{2a}{a+4}}{\frac{4a^2}{a^2−16}}\)
- إجابة
-
\(\frac{a−4}{2a}\)
\(\frac{\frac{3b}{b−5}}{\frac{b^2}{b^2−25}}\)
\(\frac{\frac{5}{c^2+5c−14}}{\frac{10}{c+7}}\)
- إجابة
-
\(\frac{1}{2(c−2)}\)
\(\frac{\frac{8}{d^2+9d+18}}{\frac{12}{d+6}}\)
\(\frac{\frac{1}{2}+\frac{5}{6}}{\frac{2}{3}+\frac{7}{9}}\)
- إجابة
-
\(\frac{24}{26}\)
\(\frac{\frac{1}{2}+\frac{3}{4}}{\frac{3}{5}+\frac{7}{10}}\)
\(\frac{\frac{2}{3}−\frac{1}{9}}{\frac{3}{4}+\frac{5}{6}}\)
- إجابة
-
\(\frac{20}{57}\)
\(\frac{\frac{1}{2}−\frac{1}{6}}{\frac{2}{3}+\frac{3}{4}}\)
\(\frac{\frac{n}{m}+\frac{1}{n}}{\frac{1}{n}−\frac{n}{m}}\)
- إجابة
-
\(\frac{n^2+m}{m−n^2}\)
\(\frac{\frac{1}{p}+\frac{p}{q}}{\frac{q}{p}−\frac{1}{q}}\)
\(\frac{\frac{1}{r}+\frac{1}{t}}{\frac{1}{r^2}−\frac{1}{t^2}}\)
- إجابة
-
\(\frac{rt}{t−r}\)
\(\frac{\frac{2}{v}+\frac{2}{w}}{\frac{1}{v^2}−\frac{1}{w^2}}\)
\(\frac{x−\frac{2x}{x+3}}{\frac{1}{x+3}+\frac{1}{x−3}}\)
- إجابة
-
\(\frac{(x+1)(x−3)}{2}\)
\(\frac{y−\frac{2y}{y−4}}{\frac{2}{y−4}−\frac{2}{y+4}}\)
\(\frac{2−\frac{2}{a+3}}{\frac{1}{a+3}+\frac{a}{2}}\)
- إجابة
-
\(\frac{4}{a+1}\)
\(\frac{4−\frac{4}{b−5}}{\frac{1}{b−5}+\frac{b}{4}}\)
في التمارين التالية، قم بالتبسيط.
\(\frac{\frac{1}{3}+\frac{1}{8}}{\frac{1}{4}+\frac{1}{12}}\)
- إجابة
-
\(\frac{1}{18}\)
\(\frac{\frac{1}{4}+\frac{1}{9}}{\frac{1}{6}+\frac{1}{12}}\)
\(\frac{\frac{5}{6}+\frac{2}{9}}{\frac{7}{18}−\frac{1}{3}}\)
- إجابة
-
19
\(\frac{\frac{1}{6}+\frac{4}{15}}{\frac{3}{5}−\frac{1}{2}}\)
\(\frac{\frac{c}{d}+\frac{1}{d}}{\frac{1}{d}−\frac{d}{c}}\)
- إجابة
-
\(\frac{c^2+c}{c−d^2}\)
\(\frac{\frac{1}{m}+\frac{m}{n}}{\frac{n}{m}−\frac{1}{n}}\)
\(\frac{\frac{1}{p}+\frac{1}{q}}{\frac{1}{p^2}−\frac{1}{q^2}}\)
- إجابة
-
\(\frac{pq}{q−p}\)
\(\frac{\frac{2}{r}+\frac{2}{t}}{\frac{1}{r^2}−\frac{1}{t^2}}\)
\(\frac{\frac{2}{x+5}}{\frac{3}{x−5}+\frac{1}{x^2−25}}\)
- إجابة
-
\(\frac{2x−10}{3x+16}\)
\(\frac{\frac{5}{y−4}}{\frac{3}{y+4}+\frac{2}{y^2−16}}\)
\(\frac{\frac{5}{z^2−64}+\frac{3}{z+8}}{\frac{1}{z+8}+\frac{2}{z−8}}\)
- إجابة
-
\(\frac{3z−19}{3z+8}\)
\(\frac{\frac{3}{s+6}+\frac{5}{s−6}}{\frac{1}{s^2−36}+\frac{4}{s+6}}\)
\(\frac{\frac{4}{a^2−2a−15}}{\frac{1}{a−5}+\frac{2}{a+3}}\)
- إجابة
-
\(\frac{4}{3a−2}\)
\(\frac{\frac{5}{b^2−6b−27}}{\frac{3}{b−9}+\frac{1}{b+3}}\)
\(\frac{\frac{5}{c+2}−\frac{3}{c+7}}{\frac{5c}{c^2+9c+14}}\)
- إجابة
-
\(\frac{2c+29}{5c}\)
\(\frac{\frac{6}{d−4}−\frac{2}{d+7}}{\frac{2d}{d^2+3d−28}}\)
\(\frac{2+\frac{1}{p−3}}{\frac{5}{p−3}}\)
- إجابة
-
\(\frac{(2p−5)}{5}\)
\(\frac{\frac{n}{n−2}}{3+\frac{5}{n−2}}\)
\(\frac{\frac{m}{m+5}}{4+\frac{1}{m−5}}\)
- إجابة
-
\(\frac{m(m−5)}{4m^2+m−95}\)
\(\frac{7+\frac{2}{q−2}}{\frac{1}{q+2}}\)
في التمارين التالية، استخدم أي من الطريقتين.
\(\frac{\frac{3}{4}−\frac{2}{7}}{\frac{1}{2}+\frac{5}{14}}\)
- إجابة
-
\(\frac{13}{24}\)
\(\frac{\frac{v}{w}+\frac{1}{v}}{\frac{1}{v}−\frac{v}{w}}\)
\(\frac{\frac{2}{a+4}}{\frac{1}{a^2−16}}\)
- إجابة
-
2 (ألف-4)
\(\frac{\frac{3}{b^2−3b−40}}{\frac{5}{b+5}−\frac{2}{b−8}}\)
\(\frac{\frac{3}{m}+\frac{3}{n}}{\frac{1}{m^2}−\frac{1}{n^2}}\)
- إجابة
-
\(\frac{3mn}{n−m}\)
\(\frac{\frac{2}{r−9}}{\frac{1}{r+9}+\frac{3}{r^2−81}}\)
\(\frac{x−\frac{3x}{x+2}}{\frac{3}{x+2}+\frac{3}{x−2}}\)
- إجابة
-
\(\frac{(x−1)(x−2)}{6}\)
\(\frac{\frac{y}{y+3}}{2+\frac{1}{y−3}}\)
الرياضيات اليومية
الإلكترونيات: مقاومة الدائرة المتكونة من خلال توصيل مقاومين بالتوازي هي\(\frac{1}{\frac{1}{R1}+\frac{1}{R2}}\)
- قم بتبسيط الكسر المعقد\(\frac{1}{\frac{1}{R1}+\frac{1}{R2}}\)
- أوجد مقاومة الدائرة عندما تكون R1=8 وR2=12
- إجابة
-
- \(\frac{R1R2}{R2+R1}\)
- \(\frac{24}{5}\)
يمكن لشركة Lenore كي الملابس أن تقوم بالكي لأعمال عائلتها في ساعات. ستستغرق ابنتها ساعتان لإنجاز عملية الكي. إذا عملت لينور وابنتها معًا، باستخدام مكويتين، فإن عدد الساعات التي سيستغرقها الأمر للقيام بكل الكي هو\(\frac{1}{\frac{1}{h}+\frac{1}{h+2}}\)
- قم بتبسيط الكسر المعقد\(\frac{1}{\frac{1}{h}+\frac{1}{h+2}}\)
- ابحث عن عدد الساعات التي ستستغرقها لينور وابنتها في العمل معًا لإنجاز عملية الكي إذا كانت h=4
تمارين الكتابة
في هذا القسم، تعلمت تبسيط الكسر المعقد\(\frac{\frac{3}{x+2}}{\frac{x}{x^2−4}}\) بطريقتين:
إعادة كتابتها كمشكلة تقسيم
ضرب البسط والمقام في شاشة LCD
ما الطريقة التي تفضلها؟ لماذا؟
- إجابة
-
سوف تتنوع الإجابات.
يريد Efraim البدء في تبسيط الكسر المعقد\(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{a}−\frac{1}{b}}\) عن طريق إلغاء المتغيرات من البسط والمقام. اشرح ما هو الخطأ في خطة إفرايم.
فحص ذاتي
ⓐ بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم إتقانك لأهداف هذا القسم.
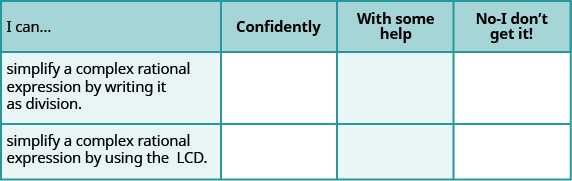
ⓑ بعد الاطلاع على قائمة التحقق، هل تعتقد أنك مستعد جيدًا للقسم التالي؟ لماذا أو لماذا لا؟


