8.2E: التمارين
- Page ID
- 200380
الممارسة تجعل من الكمال
ضرب التعبيرات الكسرية
في التمارين التالية، اضرب.
\(\frac{12}{16}·\frac{4}{10}\)
- إجابة
-
\(\frac{3}{10}\)
\(\frac{32}{5}·\frac{16}{24}\)
\(\frac{18}{10}·\frac{4}{30}\)
- إجابة
-
\(\frac{6}{25}\)
\(\frac{21}{36}·\frac{45}{24}\)
\(\frac{5x^{2}y^{4}}{12xy^3}·\frac{6x^2}{20y^2}\)
- إجابة
-
\(\frac{x^3}{8y}\)
\(\frac{8w^{3}y^9}{y^2}·\frac{3y}{4w^4}\)
\(\frac{12a^{3}b}{b^2}·\frac{2ab^2}{9b^3}\)
- إجابة
-
\(\frac{8a^4}{3b^2}\)
\(\frac{4mn^2}{5n^3}·\frac{mn^3}{8m^2}\)
\(\frac{5p^2}{p^2−5p−36}·\frac{p^2−16}{10p}\)
- إجابة
-
\(\frac{p(p−4)}{2(p−9)}\)
\(\frac{3q^2}{q^2+q−6}·\frac{q^2−9}{9q}\)
\(\frac{4r}{r^2−3r−10}·\frac{r^2−25}{8r^2}\)
- إجابة
-
\(\frac{r+5}{2r(r+2)}\)
\(\frac{s}{s^2−9s+14}·\frac{s^2−49}{7s^2}\)
\(\frac{x^2−7x}{x^2+6x+9}·\frac{x+3}{4x}\)
- إجابة
-
\(\frac{x−7}{4(x+3)}\)
\(\frac{2y^2−10y}{y^2+10y+25}·\frac{y+5}{6y}\)
\(\frac{z^2+3z}{z^2−3z−4}·\frac{z−4}{z^2}\)
- إجابة
-
\(\frac{z+3}{z(z+1)}\)
\(\frac{2a^2+8a}{a^2−9a+20}·\frac{a−5}{a^2}\)
\(\frac{28−4b}{3b−3}·\frac{b^2+8b−9}{b^2−49}\)
- إجابة
-
\(−\frac{4(b+9)}{3(b+7)}\)
\(\frac{18c−2c^2}{6c+30}·\frac{c^2+7c+10}{c^2−81}\)
\(\frac{35d−7d^2}{d^2+7d}·\frac{d^2+12d+35}{d^2−25}\)
- إجابة
-
−7
\(\frac{72m−12m^2}{8m+32}·\frac{m^2+10m+24}{m^2−36}\)
\(\frac{4n+20}{n^2+n−20}·\frac{n^2−16}{4n+16}\)
- إجابة
-
1
\(\frac{6p^2−6p}{p^2+7p−18}·\frac{p^2−81}{3p^2−27p}\)
\(\frac{q^2−2q}{q^2+6q−16}·\frac{q^2−64}{q^2−8q}\)
- إجابة
-
1
\(\frac{2r^2−2r}{r^2+4r−5}·\frac{r^2−25}{2r^2−10r}\)
في التمارين التالية، قسّم.
\(\frac{t−6}{3−t}÷\frac{t^2−9}{t−5}\)
- إجابة
-
\(−\frac{2t}{t^3−5t−9}\)
\(\frac{v−5}{11−v}÷\frac{v^2−25}{v−11}\)
\(\frac{10+w}{w−8}÷\frac{100−w^2}{8−w}\)
- إجابة
-
\(−\frac{1}{10−w}\)
\(\frac{7+x}{x−6}÷\frac{49−x^2}{x+6}\)
\(\frac{27y^2}{3y−21}÷\frac{3y^2+18}{y^2+13y+42}\)
- إجابة
-
\(\frac{3y^2(y+6)(y+7)}{(y−7)(y2+6)}\)
\(\frac{24z^2}{2z−8}÷\frac{4z−28}{z^2−11z+28}\)
\(\frac{16a^2}{4a+36}÷\frac{4a^2−24a}{a^2+4a−45}\)
- إجابة
-
\(\frac{a(a−5)}{a−6}\)
\(\frac{24b^2}{2b−4}÷\frac{12b^2+36b}{b^2−11b+18}\)
\(\frac{3c^2-16c+5}{c^2-25}÷\frac{3c^2-14c-5}{c^2+10c+25}\)
- إجابة
-
\(\frac{(3c-1)(c+5)}{(3c+1)(c−5)}\)
\(\frac{2d^2+d−3}{d^2−16}÷\frac{2d^2−9d−18}{d^2−8d+16}\)
\(\frac{6m^2−13m+2}{9−m^2}÷\frac{6m^2+23m−4}{m^2−6m+9}\)
- إجابة
-
\(−\frac{(m−2)(m−3)}{(3+m)(m+4)}\)
\(\frac{2n^2−3n−14}{25−n^2}÷\frac{2n^2−13n+21}{n^2−10n+25}\)
\(\frac{3s^2}{s^2−16}÷\frac{s^3+4s^2+16s}{s^3−64}\)
- إجابة
-
\(\frac{3s}{s+4}\)
\(\frac{r^2−9}{15}÷\frac{r^3−27}{5r^2+15r+45}\)
\(\frac{p^3+q^3}{3p^2+3pq+3q^2}÷\frac{p^2−q^2}{12}\)
- إجابة
-
\(\frac{4(p^2−pq+q^2)}{(p−q)(p^2+pq+q^2)}\)
\(\frac{v^3−8w^3}{2v^2+4vw+8w^2}÷\frac{v^2−4w^2}{4}\)
\(\frac{t^2−9}{2t}÷(t^2−6t+9)\)
- إجابة
-
\(\frac{t+3}{2t(t−3)}\)
\(\frac{x^2+3x−10}{4x}÷(2x^2+20x+50)\)
\(\frac{2y^2−10yz−48z^2}{2y−1}÷(4y^2−32yz)\)
- إجابة
-
\(\frac{y+3z}{2y(2y−1)}\)
\(\frac{2m^2−98n^2}{2m+6}÷(m^2−7mn)\)
\(\frac{\frac{2a^2−a−21}{5a+20}}{\frac{a^2+7a+12}{a^2+8a+16}}\)
- إجابة
-
\(\frac{2a−7}{5}\)
\(\frac{\frac{3b^2+2b−8}{12b+18}}{\frac{3b^2+2b−8}{2b^2−7b−15}}\)
\(\frac{\frac{12c^2−12}{2c^2−3c+14}}{\frac{c+4}{6c^2−13c+5}}\)
- إجابة
-
3 (3c−5)
\(\frac{\frac{4d^2+7d−2}{35d+10}}{\frac{d^2−4}{7d^2−12d−4}}\)
\(\frac{10m^2+80m}{3m−9}·\frac{m^2+4m−21}{m^2−9m+20}÷\frac{5m^2+10m}{2m−10}\)
- إجابة
-
\(\frac{4(m+8)(m+7)}{3(m−4)(m+2)}\)
\(\frac{4n^2+32n}{3n+2}·\frac{3n^2−n−2}{n^2+n−30}÷\frac{108n^2−24n}{n+6}\)
\(\frac{12p^2+3p}{p+3}÷\frac{p^2+2p−63}{p^2−p−12}·\frac{p−7}{9p^3−9p^2}\)
- إجابة
-
\(\frac{(4p+1)(p−7)}{3p(p+9)(p−1)}\)
\(\frac{6q+3}{9q^2−9q}÷\frac{q^2+14q+33}{q^2+4q−5}·\frac{4q^2+12q}{12q+6}\)
الرياضيات اليومية
الاحتمال يقوم مدير شركة كبيرة بإجراء مقابلات مع المتقدمين لوظيفتين متطابقتين. إذا كان w = عدد النساء المتقدمات و m= عدد المتقدمين من الرجال، فإن احتمال اختيار امرأتين للوظائف هو\(\frac{w}{w+m}·\frac{w−1}{w+m−1}\).
- قم بتبسيط الاحتمال بضرب التعبيرين العقاريين.
- أوجد احتمال اختيار امرأتين عند w=5 وm=10.
- إجابة
-
- \(\frac{w(w−1)}{(w+m)(w+m−1)}\)
- \(\frac{2}{21}\)
مساحة المثلث مساحة المثلث ذو القاعدة b والارتفاع h هو\(\frac{bh}{2}\). إذا كان المثلث ممتدًا لإنشاء مثلث جديد بقاعدته وارتفاعه ثلاثة أضعاف ما هو عليه في المثلث الأصلي، تكون المساحة هي\(\frac{9bh}{2}\). احسب كيفية مقارنة مساحة المثلث الجديد بمساحة المثلث الأصلي\(\frac{9bh}{2}\) بالقسمة على\(\frac{bh}{2}\).
تمارين الكتابة
- اضرب\(\frac{7}{4}·\frac{9}{10}\) واشرح جميع خطواتك.
- اضرب\(\frac{n}{n−3}·\frac{9n+3}{n}\) واشرح جميع خطواتك.
- قم بتقييم إجابتك على الجزء (ب) عندما n = 7. هل حصلت على نفس الإجابة التي حصلت عليها في الجزء (أ)؟ لماذا أو لماذا لا؟
- إجابة
-
سوف تتنوع الإجابات.
- قسّم\(\frac{24}{5}÷6\) واشرح جميع خطواتك.
- قسّم\(\frac{x^2−1}{x}÷(x+1)\) واشرح جميع خطواتك.
- قم بتقييم إجابتك على الجزء (ب) عندما x = 5. هل حصلت على نفس الإجابة التي حصلت عليها في الجزء (أ)؟ لماذا أو لماذا لا؟
فحص ذاتي
ⓐ بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم إتقانك لأهداف هذا القسم.
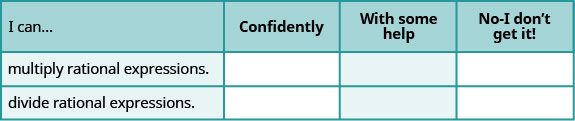
ⓑ بعد مراجعة قائمة التحقق هذه، ماذا ستفعل لتصبح واثقًا من جميع الأهداف؟


