8.2: ضرب التعبيرات الكسرية وقسمتها
- Page ID
- 200370
في نهاية هذا القسم، ستكون قادرًا على:
- اضرب التعبيرات العقلانية
- اقسم التعبيرات العقلانية
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
إذا فاتتك مشكلة، فارجع إلى القسم المدرج وراجع المادة.
- اضرب:\(\frac{14}{15}·\frac{6}{35}\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.6.13. - قسّم:\(\frac{14}{15}÷\frac{6}{35}\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.6.22. - عامل بالكامل:\(2x^2−98\).
إذا فاتتك هذه المشكلة، راجع التمرين 7.5.10. - عامل بالكامل:\(10n^3+10\).
إذا فاتتك هذه المشكلة، راجع التمرين 7.5.19. - عامل بالكامل:\(10p^2−25pq−15q^2\).
إذا فاتتك هذه المشكلة، راجع التمرين 7.5.28.
ضرب التعبيرات الكسرية
لضرب المقادير الكسرية، نقوم بما فعلناه بالكسور العددية. نضرب البسط ونضرب القواسم. ثم، إذا كانت هناك أي عوامل مشتركة، فإننا نزيلها لتبسيط النتيجة.
إذا كانت p أو q أو s عبارة عن كثيرات الحدود حيث\(q \ne 0\) و\(s \ne 0\)
\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)لضرب التعبيرات العقلانية، اضرب البسط واضرب المقامات.
سنقوم بعمل المثال الأول مع الكسور العددية لتذكيرنا بكيفية ضرب الكسور بدون متغيرات.
اضرب:\(\frac{10}{28}·\frac{8}{15}\).
- إجابة
-
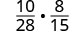
اضرب البسط والمقامات. 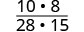
ابحث عن العوامل المشتركة، ثم قم بإزالتها. 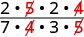
قم بالتبسيط. 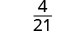
الضرب:\(\frac{6}{10}·\frac{15}{12}\).
- إجابة
-
\(\frac{3}{4}\)
الضرب:\(\frac{20}{15}·\frac{6}{8}\).
- إجابة
-
1
تذكر أننا سنفترض خلال هذا الفصل أن جميع القيم العددية التي تجعل المقام صفرًا مستبعدة. لن نكتب القيود الخاصة بكل تعبير عقلاني، ولكن ضع في اعتبارك أن المقام لا يمكن أن يكون صفرًا أبدًا. لذا في هذا المثال التالي،\(x \ne 0\) and \(y \ne 0\).
الضرب:\(\frac{2x}{3y^2}·\frac{6xy^3}{x^{2}y}\).
- إجابة
-
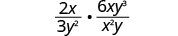
اضرب. 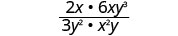
قم بحساب البسط والمقام بالكامل، ثم قم بإزالة العوامل المشتركة. 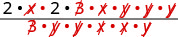
قم بالتبسيط. 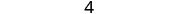
الضرب:\(\frac{3pq}{q^2}·\frac{5p^{2}q}{6pq}\).
- إجابة
-
\(\frac{5p^2}{2q}\)
الضرب:\(\frac{6x^{3}y}{7x^2}·\frac{2xy}{3x^{2}y}\).
- إجابة
-
\(\frac{12y^3}{7}\)
كيفية ضرب التعبيرات العقلانية
الضرب:\(\frac{2x}{x^2-7x+12}·\frac{x^2−9}{6x^2}\).
- إجابة
-
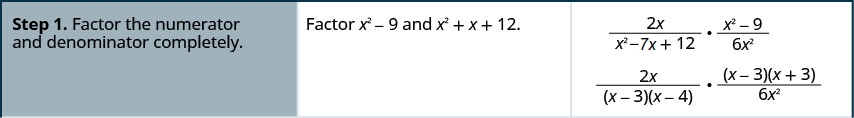


الضرب:\(\frac{5x}{x^2+5x+6}·\frac{x^2−4}{10x}\).
- إجابة
-
\(\frac{x−2}{2(x+3)}\)
الضرب:\(\frac{9x^2}{x^2+11x+30}·\frac{x^2−36}{3x^2}\).
- إجابة
-
\(\frac{3(x−6)}{x+5}\)
- قم بحساب كل من البسط والمقام بالكامل.
- اضرب البسط والمقامات.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
اضرب:\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\).
- إجابة
-
\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\) ضع في اعتبارك كل من البسط والمقام. \(\frac{n(n−7)}{(n+1)(n+1)}·\frac{n+1}{2n}\) اضرب البسط والمقامات. \(\frac{n(n−7)(n+1)}{(n+1)(n+1)2n}\) قم بالتبسيط. \(\frac{n−7}{2(n+1)}\)
اضرب:\(\frac{x^2−25}{x^2−3x−10}·\frac{x+2}{x}\).
- إجابة
-
\(\frac{x+5}{x}\)
اضرب:\(\frac{x^2−4x}{x^2+5x+6}·\frac{x+2}{x}\).
- إجابة
-
\(\frac{x−4}{x+3}\)
اضرب:\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\).
- إجابة
-
\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\) ضع في اعتبارك كل من البسط والمقام. \(\frac{4(4−x)}{2(x−6)}·\frac{(x−6)(x+1)}{(x−4)(x+4)}\) اضرب البسط والمقامات. \(\frac{4(4−x)(x−6)(x+1)}{2(x−6)(x−4)(x+4)}\) قم بالتبسيط. \(−\frac{2(x+1)}{(x+4)}\)
اضرب:\(\frac{12x−6x^2}{x^2+8x}·\frac{x^2+11x+24}{x^2−4}\).
- إجابة
-
\(−\frac{6(x+3)}{x+2}\)
اضرب:\(\frac{9v−3v^2}{9v+36}·\frac{v^2+7v+12}{v^2−9}\).
- إجابة
-
\(−\frac{v}{3}\)
اضرب:\(\frac{2x−6}{x^2−8x+15}·\frac{x^2−25}{2x+10}\).
- إجابة
-
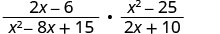
ضع في اعتبارك كل من البسط والمقام. 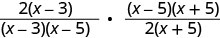
اضرب البسط والمقامات. 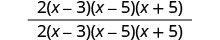
قم بإزالة العوامل المشتركة. 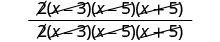
قم بالتبسيط. 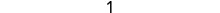
اضرب:\(\frac{3a−21}{a^2−9a+14}·\frac{a^2−4}{3a+6}\).
- إجابة
-
1
اضرب:\(\frac{b^2−b}{b^2+9b−10}·\frac{b^2−100}{b^2−10b}\).
- إجابة
-
1
قسمة التعبيرات الكسرية
لتقسيم المقادير الكسرية، نضرب الكسر الأول في مقلوب الثاني، تمامًا كما فعلنا مع الكسور العددية.
تذكر أن المعاملة بالمثل\(\frac{a}{b}\) هي\(\frac{b}{a}\). لإيجاد المقلوب، نضع البسط ببساطة في المقام والمقام في البسط. نحن «نقلب» الكسر.
إذا كانت p أو q أو s عبارة عن كثيرات الحدود حيث\(q \ne 0\)\(r \ne 0\)،\( s \ne 0\)
\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
لتقسيم التعبيرات العقلانية، اضرب الكسر الأول في مقلوب الثاني.
كيفية تقسيم التعبيرات العقلانية
قسّم:\(\frac{x+9}{6−x}÷\frac{x^2−81}{x−6}\).
- إجابة
-




قسّم:\(\frac{c+3}{5−c}÷\frac{c^2−9}{c−5}\).
- إجابة
-
\(−\frac{1}{c−3}\)
قسّم:\(\frac{2−d}{d−4}÷\frac{4−d^2}{4−d}\).
- إجابة
-
\(−\frac{1}{2+d}\)
- أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني.
- ضع البسط والمقامات في الاعتبار بشكل كامل.
- اضرب البسط والمقامات معًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
قسّم:\(\frac{3n^2}{n^2−4n}÷\frac{9n^2−45n}{n^2−7n+10}\).
- إجابة
-
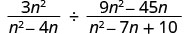
أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني. 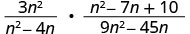
ضع البسط والمقامات في الاعتبار ثم اضرب. 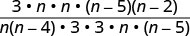
قم بالتبسيط من خلال تقسيم العوامل المشتركة. 
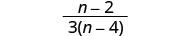
قسّم:\(\frac{2m^2}{m^2−8m}÷\frac{8m^2+24m}{m^2+m−6}\).
- إجابة
-
\(\frac{(m−2)}{4(m−8)}\)
قسّم:\(\frac{15n^2}{3n^2+33n}÷\frac{5n−5}{n^2+9n−22}\).
- إجابة
-
\(\frac{n(n−2)}{n−1}\)
تذكر أولاً إعادة كتابة القسمة كضرب للتعبير الأول في مقلوب الثاني. ثم ضع في اعتبارك كل شيء وابحث عن العوامل المشتركة.
قسّم:\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\).
- إجابة
-
\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\) أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني. \(\frac{2x^2+5x−12}{x^2−16}·\frac{x^2−8x+16}{2x^2−13x+15}\) ضع البسط والمقامات في الاعتبار ثم اضرب. \(\frac{(2x−3)(x+4)(x−4)(x−4)}{(x−4)(x+4)(2x−3)(x−5)}\) قم بالتبسيط. \(\frac{(x−4)}{(x−5)}\)
قسّم:\(\frac{3a^2−8a−3}{a^2−25}÷\frac{3a^2−14a−5}{a^2+10a+25}\).
- إجابة
-
\(\frac{(a−3)(a+5)}{(a−5)(a−5)}\)
قسّم:\(\frac{4b^2+7b−2}{1−b^2}÷\frac{4b^2+15b−4}{b^2−2b+1}\).
- إجابة
-
\(−\frac{(b+2)(b−1)}{(1+b)(b+4)}\)
قسّم:\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\).
- إجابة
-
\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\) أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني. \(\frac{p^3+q^3}{2p^2+2pq+2q^2}·\frac{6}{p^2−q^2}\) ضع البسط والمقامات في الاعتبار ثم اضرب. \(\frac{(p+q)(p^2−pq+q^2)6}{2(p^2+pq+q^2)(p−q)(p+q)}\) قم بالتبسيط. \(\frac{3(p^2−pq+q^2)}{(p−q)(p^2+pq+q^2)}\)
قسّم:\(\frac{x^3−8}{3x^2−6x+12}÷\frac{x^2−4}{6}\).
- إجابة
-
\(\frac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
قسّم:\(\frac{2z^2}{z^2−1}÷\frac{z^3−z^2+z}{z^3−1}\).
- إجابة
-
\(\frac{2z(z^2+z+1)}{(z+1)(z^2−z+1)}\)
قبل القيام بالمثال التالي، دعونا ننظر إلى كيفية تقسيم الكسر على عدد صحيح. عندما نقسم\(\frac{3}{5}÷4\)
\[\begin{array}{c} {\frac{3}{5}÷4}\\ {\frac{3}{5}÷\frac{4}{1}}\\ {\frac{3}{5}·\frac{1}{4}}\\ \nonumber \end{array}\]
نحن نفعل نفس الشيء عندما نقسم التعبيرات العقلانية.
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\).
- إجابة
-
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\) اكتب التعبير الثاني في صورة كسر. \(\frac{a^2−b^2}{3ab}÷\frac{a^2+2ab+b^2}{1}\) أعد كتابة القسمة كتعبير أول مضروبًا في مقلوب التعبير الثاني. \(\frac{a^2−b^2}{3ab}·\frac{1}{a^2+2ab+b^2}\) ضع البسط والمقامات في الاعتبار، ثم اضرب. \(\frac{(a−b)(a+b)1}{3ab·(a+b)(a+b)}\) قم بالتبسيط. \(\frac{a−b}{3ab(a+b)}\)
\(\frac{2x^2−14x−16}{4}÷(x2+2x+1)\).
- إجابة
-
\(\frac{x−8}{2(x+1)}\)
\(\frac{y^2−6y+8}{y^2−4y}÷(3y2−12y)\).
- إجابة
-
\(\frac{y−2}{3y(y−4)}\)
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\).
- إجابة
-
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\) أعد الكتابة بعلامة القسمة. \(\frac{6x^2−7x+2}{4x−8}÷\frac{2x^2−7x+3}{x^2−5x+6}\) أعد الكتابة كمنتج لأول مرة مقابل الثانية. \(\frac{6x^2−7x+2}{4x−8}·\frac{x^2−5x+6}{2x^2−7x+3}\) ضع البسط والمقامات في الاعتبار، ثم اضرب \(\frac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)}\) قم بالتبسيط. \(\frac{3x−2}{4}\)
\(\frac{\frac{3x^2+7x+2}{4x+24}}{\frac{3x^2−14x−5}{x^2+x−30}}\).
- إجابة
-
\(\frac{x+2}{4}\)
\(\frac{\frac{y^2−36}{2y^2+11y−6}}{\frac{2y^2−2y−60}{8y−4}}\).
- إجابة
-
\(\frac{2}{y+5}\)
إذا كان لدينا أكثر من تعبيرين منطقيين للعمل بهما، فإننا لا نزال نتبع نفس الإجراء. ستكون الخطوة الأولى هي إعادة كتابة أي قسمة كضرب في المعاملة بالمثل. ثم نأخذ في الاعتبار ونضاعف.
\(\frac{3x−6}{4x−4}·\frac{x^2+2x−3}{x^2−3x−10}÷\frac{2x+12}{8x+16}\).
- إجابة
-
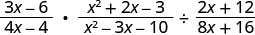
أعد كتابة القسمة في صورة ضرب في المقلوب. 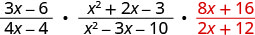
ضع البسط والمقامات في الاعتبار، ثم اضرب. 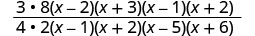
قم بالتبسيط من خلال تقسيم العوامل المشتركة. 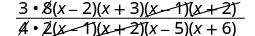
قم بالتبسيط. 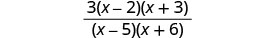
\(\frac{4m+4}{3m−15}·\frac{m^2−3m−10}{m^2−4m−32}÷\frac{12m−36}{6m−48}\).
- إجابة
-
\(\frac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
\(\frac{2n^2+10n}{n−1}÷\frac{n^2+10n+24}{n^2+8n−9}·\frac{n+4}{8n^2+12n}\).
- إجابة
-
\(\frac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
المفاهيم الرئيسية
- ضرب التعبيرات الكسرية
- إذا كانت p أو q أو r أو s عبارة عن كثيرات الحدود\(s \ne 0\) حيث\(q \ne 0\) ثم\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)
- لضرب التعبيرات المنطقية، اضرب البسط واضرب المقامات
- اضرب مقدارًا كسريًا
- قم بحساب كل من البسط والمقام بالكامل.
- اضرب البسط والمقامات.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
- قسم التعبيرات الكسرية
- إذا كانت p أو q أو s عبارة عن كثيرات الحدود حيث\(q \ne 0\)،\(r \ne 0\)،\( s \ne 0\)، إذن\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
- لتقسيم التعبيرات العقلانية، اضرب الكسر الأول في مقلوب الثاني.
- قسمة التعبيرات الكسرية
- أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني.
- ضع البسط والمقامات في الاعتبار تمامًا.
- اضرب البسط والمقامات معًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.


