8.1E: تمارين
- Page ID
- 200369
الممارسة تجعل من الكمال
في التمارين التالية، حدد القيم التي لم يتم تعريف التعبير العقلاني لها.
- \(\dfrac{2x}{z}\)
- \(\dfrac{4p−1}{6p−5}\)
- \(\dfrac{n−3}{n^2+2n−8}\)
- إجابة
-
- ض = 0
- \(p=\dfrac{5}{6}\)
- ن=−4، ن = 2
- \(\dfrac{10m}{11n}\)
- \(\dfrac{6y+13}{4y−9}\)
- \(\dfrac{b−8}{b^2−36}\)
- \(\dfrac{4x^{2}y}{3y}\)
- \(\dfrac{3x−2}{2x+1}\)
- \(\dfrac{u−1}{u^2−3u−28}\)
- إجابة
-
- ص = 0
- \(x=−\dfrac{1}{2}\)
- u=−4، u=7
- \(\dfrac{5pq^{2}}{9q}\)
- \(\dfrac{7a−4}{3a+5}\)
- \(\dfrac{1}{x^2−4}\)
إيجاد قيمة التعبيرات الكسرية
في التمارين التالية، قم بتقييم التعبير العقلاني للقيم المُعطاة.
\(\dfrac{2x}{x−1}\)
- س = 0
- س = 2
- x=−1
- إجابة
-
- 0
- 4
- 1
\(\dfrac{4y−1}{5y−3}\)
- ص = 0
- ص = 2
- y=−1
\(\dfrac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=−2
- إجابة
-
- 3
- \(\dfrac{5}{2}\)
- \(−\dfrac{1}{5}\)
\(\dfrac{x+3}{2−3x}\)
- س = 0
- س = 1
- x=−2
\(\dfrac{y^2+5y+6}{y^2−1}\)
- ص = 0
- ص = 2
- y=−2
- إجابة
-
- −6
- \(\dfrac{20}{3}\)
- 0
\(\dfrac{z^2+3z−10}{z^2−1}\)
- ض = 0
- z = 2
- z=−2
\(\dfrac{a^2−4}{a^2+5a+4}\)
- أ=0
- أ=1
- a=−2
- إجابة
-
- −1
- \(−\dfrac{3}{10}\)
- 0
\(\dfrac{b^2+2}{b^2−3b−4}\)
- ب = 0
- ب = 2
- ب = −2
\(\dfrac{x^2+3xy+2y^2}{2x^{3}y}\)
- س = 1، ص = −1
- س = 2، ص = 1
- x=−1، y=−2
- إجابة
-
- 0
- \(\dfrac{3}{4}\)
- \(\dfrac{15}{4}\)
\(\dfrac{c^2+cd−2d^2}{cd^{3}}\)
- c=2، d=−1
- c=1، d=−1
- c=−1، d=2
\(\dfrac{m^2−4n^2}{5mn^3}\)
- م = 2، ن = 1
- m=−1، n=−1
- م = 3، ن = 2
- إجابة
-
- 0
- \(−\dfrac{3}{5}\)
- \(−\dfrac{7}{20}\)
\(\dfrac{2s^{2}t}{s^2−9t^2}\)
- s=4، t=1
- s=−1، t=−1
- s=0، t=2
تبسيط التعبيرات الكسرية
في التمارين التالية، قم بالتبسيط.
\(−\dfrac{4}{52}\)
- إجابة
-
\(−\dfrac{1}{13}\)
\(−\dfrac{44}{55}\)
\(\dfrac{56}{63}\)
- إجابة
-
\(\dfrac{8}{9}\)
\(\dfrac{65}{104}\)
\(\dfrac{6ab^{2}}{12a^{2}b}\)
- إجابة
-
\(\dfrac{b}{2a}\)
\(\dfrac{15xy^{3}}{x^{3}y^{3}}\)
\(\dfrac{8m^{3}n}{12mn^2}\)
- إجابة
-
\(\dfrac{2m^2}{3n}\)
\(\dfrac{36v^{3}w^2}{27vw^3}\)
\(\dfrac{3a+6}{4a+8}\)
- إجابة
-
\(\dfrac{3}{4}\)
\(\dfrac{5b+5}{6b+6}\)
\(\dfrac{3c−9}{5c−15}\)
- إجابة
-
\(\dfrac{3}{5}\)
\(\dfrac{4d+8}{9d+18}\)
\(\dfrac{7m+63}{5m+45}\)
- إجابة
-
\(\dfrac{7}{5}\)
\(\dfrac{8n−96}{3n−36}\)
\(\dfrac{12p−240}{5p−100}\)
- إجابة
-
\(\dfrac{12}{5}\)
\(\dfrac{6q+210}{5q+175}\)
\(\dfrac{a^2−a−12}{a^2−8a+16}\)
- إجابة
-
\(\dfrac{a+3}{a−4}\)
\(\dfrac{x^2+4x−5}{x^2−2x+1}\)
\(\dfrac{y^2+3y−4}{y^2−6y+5}\)
- إجابة
-
\(\dfrac{y+4}{y−5}\)
\(\dfrac{v^2+8v+15}{v^2−v−12}\)
\(\dfrac{x^2−25}{x^2+2x−15}\)
- إجابة
-
\(\dfrac{x−5}{x−3}\)
\(\dfrac{a^2−4}{a^2+6a−16}\)
\(\dfrac{y^2−2y−3}{y^2−9}\)
- إجابة
-
\(\dfrac{y+1}{y+3}\)
\(\dfrac{b^2+9b+18}{b^2−36}\)
\(\dfrac{y^3+y^2+y+1}{y^2+2y+1}\)
- إجابة
-
\(\dfrac{y^2+1}{y+1}\)
\(\dfrac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\dfrac{x^3−2x^2−25x+50}{x^2−25}\)
- إجابة
-
x−2
\(\dfrac{q^3+3q^2−4q−12}{q^2−4}\)
\(\dfrac{3a^2+15a}{6a^2+6a−36}\)
- إجابة
-
\(\dfrac{a(a+5)}{2(a+3)(a−2)}\)
\(\dfrac{8b^2−32b}{2b^2−6b−80}\)
\(\dfrac{−5c^2−10c}{−10c^2+30c+100}\)
- إجابة
-
\(\dfrac{c}{2(c−5)}\)
\(\dfrac{4d^2−24d}{2d^2−4d−48}\)
\(\dfrac{3m^2+30m+75}{4m^2−100}\)
- إجابة
-
\(\dfrac{3(m+5)}{4(m−5)}\)
\(\dfrac{5n^2+30n+45}{2n^2−18}\)
\(\dfrac{5r^2+30r−35}{r^2−49}\)
- إجابة
-
\(\dfrac{5(r−1)}{r+7}\)
\(\dfrac{3s^2+30s+72}{3s^2−48}\)
\(\dfrac{t^3−27}{t^2−9}\)
- إجابة
-
\(\dfrac{t^2+3t+9}{t+3}\)
\(\dfrac{v^3−1}{v^2−1}\)
\(\dfrac{w^3+216}{w^2−36}\)
- إجابة
-
\(\dfrac{w^2−6w+36}{w−6}\)
\(\dfrac{v^3+125}{v^2−25}\)
تبسيط التعبيرات الكسرية باستخدام العوامل المعاكسة
في التمارين التالية، قم بتبسيط كل تعبير عقلاني.
\(\dfrac{a−5}{5−a}\)
- إجابة
-
−1
\(\dfrac{b−12}{12−b}\)
\(\dfrac{11−c}{c−11}\)
- إجابة
-
−1
\(\dfrac{5−d}{d−5}\)
\(\dfrac{12−2x}{x^2−36}\)
- إجابة
-
\(−\dfrac{2}{x+6}\)
\(\dfrac{20−5y}{y^2−16}\)
\(\dfrac{4v−32}{64−v^2}\)
- إجابة
-
\(−\dfrac{4}{8+v}\)
\(\dfrac{7w−21}{9−w^2}\)
\(\dfrac{y^2−11y+24}{9−y^2}\)
- إجابة
-
\(−\dfrac{y−8}{3+y}\)
\(\dfrac{z^2−9z+20}{16−z^2}\)
\(\dfrac{a^2−5a−36}{81−a^2}\)
- إجابة
-
\(−\dfrac{a+4}{9+a}\)
\(\dfrac{b^2+b−42}{36−b^2}\)
الرياضيات اليومية
معدلات الضرائب بالنسبة للسنة الضريبية 2015، يمكن العثور على مبلغ الضريبة المستحقة على شخص واحد يكسب ما بين 37,450 دولارًا و 90,750 دولارًا، من خلال تقييم الصيغة 0.25x−4206.25، حيث x هي الدخل. يمكن العثور على متوسط معدل الضريبة لهذا الدخل من خلال تقييم الصيغة\(\dfrac{0.25x−4206.25}{x}\). ما هو متوسط معدل الضريبة لشخص واحد يكسب 50,000 دولار؟
- إجابة
-
16.5%
العمل يمكن العثور على طول الوقت الذي يستغرقه شخصان لأداء نفس المهمة إذا عملوا معًا من خلال تقييم الصيغة\(\dfrac{xy}{x+y}\). إذا كان توم قادرًا على طلاء العرين في x=45 دقيقة وكان بإمكان شقيقه بوبي رسمه في y=60 دقيقة، فما عدد الدقائق التي سيستغرقها العمل معًا؟
تمارين الكتابة
اشرح كيفية العثور على قيم x التي لم\(\dfrac{x^2−x−20}{x^2−4}\) يتم تعريف التعبير العقلاني لها.
- إجابة
-
ستختلف الإجابات، ولكن يجب أن تشير جميعها إلى إعداد دالة المقام إلى الصفر.
اشرح جميع الخطوات التي تتخذها لتبسيط التعبير العقلاني\(\dfrac{p^2+4p−21}{9−p^2}\).
فحص ذاتي
ⓐ بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم إتقانك لأهداف هذا القسم.
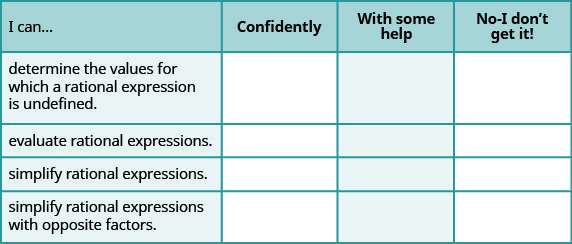
ⓑ إذا كانت معظم الشيكات الخاصة بك:
... بثقة. تهانينا! لقد حققت أهدافك في هذا القسم! فكر في مهارات الدراسة التي استخدمتها حتى تتمكن من الاستمرار في استخدامها. ماذا فعلت لتصبح واثقًا من قدرتك على القيام بهذه الأشياء؟ كن محددًا!
... مع بعض المساعدة. يجب معالجة هذا بسرعة لأن الموضوعات التي لا تتقنها تصبح ثقوبًا في طريقك إلى النجاح. الرياضيات متسلسلة - كل موضوع يعتمد على العمل السابق. من المهم التأكد من أن لديك أساسًا قويًا قبل المضي قدمًا. من الذي يمكنك طلب المساعدة؟ يعتبر زملائك في الفصل والمدرب موارد جيدة. هل يوجد مكان في الحرم الجامعي حيث يتوفر مدرسو الرياضيات؟ هل يمكن تحسين مهاراتك الدراسية؟
... لا - أنا لا أفهم ذلك! هذا أمر بالغ الأهمية ويجب ألا تتجاهله. تحتاج إلى الحصول على المساعدة على الفور وإلا ستصاب بالارتباك بسرعة. راجع مدرسك في أقرب وقت ممكن لمناقشة وضعك. معًا يمكنك وضع خطة للحصول على المساعدة التي تحتاجها.


