8.1: تبسيط التعبيرات الكسرية
- Page ID
- 200360
في نهاية هذا القسم، ستكون قادرًا على:
- حدد القيم التي لا يتم تعريف التعبير العقلاني لها
- تقييم التعبيرات العقلانية
- تبسيط التعبيرات العقلانية
- قم بتبسيط التعبيرات العقلانية باستخدام العوامل المعاكسة
في الفصل الأول، استعرضنا خصائص الكسور وعملياتها. قدّمنا الأعداد النسبية، وهي مجرد كسور يكون فيها البسط والمقامات أعدادًا صحيحة، والمقام ليس صفرًا.
في هذا الفصل، سوف نتعامل مع الكسور التي يكون البسط والمقامات الخاصة بها كثيرات الحدود. نسمي هذه التعبيرات العقلانية.
التعبير العقلاني هو تعبير عن الشكل\(\frac{p(x)}{q(x)}\)، حيث p و q هما كثيرات الحدود و\(q \ne 0\).
فيما يلي بعض الأمثلة على التعبيرات العقلانية:
\[\begin{array}{cccc} {−\frac{13}{42}}&{\frac{7y}{8z}}&{\frac{5x+2}{x^2−7}}&{\frac{4x^2+3x−1}{2x−8}}\\ \nonumber \end{array}\]
لاحظ أن التعبير العقلاني الأول المذكور أعلاه\(−\frac{13}{42}\)،، هو مجرد كسر. نظرًا لأن الثابت هو كثير الحدود بدرجة صفر، فإن نسبة الثوابتين هي تعبير نسبي، بشرط ألا يكون المقام صفرًا.
سنقوم بنفس العمليات باستخدام التعبيرات النسبية التي نقوم بها مع الكسور. سنقوم بتبسيطها وإضافتها وطرحها وضربها وقسمتها واستخدامها في التطبيقات.
حدد القيم التي لا يتم تعريف التعبير العقلاني لها
عندما نتعامل مع كسر عددي، يكون من السهل تجنب القسمة على الصفر، لأننا نستطيع رؤية الرقم في المقام. لتجنب القسمة على الصفر في التعبير العقلاني، يجب ألا نسمح بقيم المتغير التي تجعل المقام صفرًا.
إذا كان المقام هو صفر، فإن التعبير العقلاني غير معرف. قد يكون بسط التعبير العقلاني هو 0 - ولكن ليس المقام.
لذا قبل أن نبدأ أي عملية باستخدام تعبير نسبي، نفحصها أولاً لإيجاد القيم التي تجعل المقام صفرًا. بهذه الطريقة، عندما نحل معادلة عقلانية على سبيل المثال، سنعرف ما إذا كانت الحلول الجبرية التي نجدها مسموح بها أم لا.
- عيّن المقام مساويًا للصفر.
- حل المعادلة في مجموعة القيم الحقيقية، إن أمكن.
حدد القيم التي لم يتم تعريف التعبير العقلاني لها:
- \(\frac{9y}{x}\)
- \(\frac{4b−3}{2b+5}\)
- \(\frac{x+4}{x^2+5x+6x}\)
الحل
لن يتم تعريف التعبير عندما يكون المقام صفرًا.
| 1. | \(\frac{9y}{x}\) |
| عيّن المقام مساويًا للصفر. حل للمتغير. | س = 0 |
| \(\frac{9y}{x}\)غير معرف لـ x=0. | |
| 2. |
\(\frac{4b−3}{2b+5}\) |
| عيّن المقام مساويًا للصفر. حل للمتغير. | 2b+5=0 |
| 2b=−5 | |
| \(b=−\frac{5}{2}\) | |
| \(\frac{4b−3}{2b+5}\)غير معرف لـ\(b=−\frac{5}{2}\). | |
| 3. | \(\frac{x+4}{x^2+5x+6x}\) |
| عيّن المقام مساويًا للصفر. حل للمتغير. | \(x^2+5x+6x=0\) |
| \((x+2)(x+3)=0\) | |
| x+2=0 أو x+3=0 | |
| x=−2 أو x=−3 | |
| \(\frac{x+4}{x^2+5x+6x}\)غير معرّف لـ x=−2 أو x=−3. |
إن القول بأن التعبير العقلاني\(\frac{x+4}{x^2+5x+6x}\) غير معرف لـ x=−2orx=−3 يشبه كتابة عبارة «باطلة حيث تكون محظورة» في قواعد المسابقة.
جرب ذلك\(\PageIndex{2}\)
حدد القيم التي لم يتم تعريف التعبير العقلاني لها:
- \(\frac{3y}{x}\)
- \(\frac{8n−5}{3n+1}\)
- \(\frac{a+10}{a^2+4a+3a}\)
- Answer
-
- x=0
- \(n=−\frac{1}{3}\)
- a=−1, a=−3
Try It \(\PageIndex{3}\)
حدد القيم التي لم يتم تعريف التعبير العقلاني لها:
- \(\frac{4p}{5q}\)
- \(\frac{y−1}{3y+2}\)
- \(\frac{m−5}{m^2+m−6}\)
- إجابة
-
- س = 0
- \(y=−\frac{2}{3}\)
- m=2، m=−3
إيجاد قيمة التعبيرات الكسرية
لتقييم التعبير العقلاني، نستبدل قيم المتغيرات في التعبير ونبسطه، تمامًا كما فعلنا مع العديد من التعبيرات الأخرى في هذا الكتاب.
قم\(\frac{2x+3}{3x−5}\) بالتقييم لكل قيمة:
- س = 0
- س = 2
- x=−3
الحل
| 1. |  |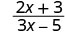
 |
 |
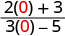| قم بالتبسيط. |  |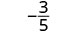
| 2. |  |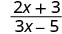
 |
 |
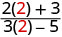| قم بالتبسيط. |  |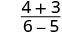
 |
|
 |
|
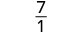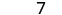| 3. |  |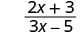
 |
 |
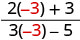| قم بالتبسيط. |  |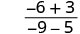
 |
|
 |
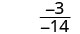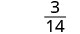جرب ذلك\(\PageIndex{5}\)
تقييم\(\frac{y+1}{2y−3}\) for each value:
- y=1
- y=−3
- y=0
- Answer
-
- −2
- \(\frac{2}{9}\)
- \(−\frac{1}{3}\)
Try It \(\PageIndex{6}\)
قم\(\frac{5x−1}{2x+1}\) بالتقييم لكل قيمة:
- س = 1
- x=−1
- س = 0
- إجابة
-
- \(\frac{4}{3}\)
- 6
- −1
قم\(\frac{x^2+8x+7}{x^2−4}\) بالتقييم لكل قيمة:
- س = 0
- س = 2
- x=−1
الحل
| 1. |  |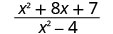
 |
 |
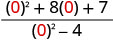| قم بالتبسيط. |  |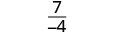
 |
|
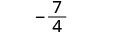| 2. | |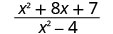
 |
 |
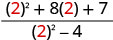| قم بالتبسيط. |  |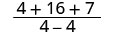
 |
|
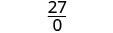| هذا التعبير العقلاني غير معرف لـ x = 2. | |
| 3. |  |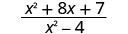
 |
 |
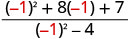| قم بالتبسيط. |  |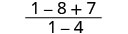
 |
|
 |
|
 |
|
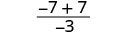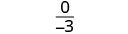جرب ذلك\(\PageIndex{8}\)
تقييم\(\frac{x^2+1}{x^2−3x+2}\) for each value:
- x=0
- x=−1
- x=3
- Answer
-
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- 2
Try It \(\PageIndex{9}\)
قم\(\frac{x^2+x−6}{x^2−9}\) بالتقييم لكل قيمة.
- س = 0
- x=−2
- س = 1
- إجابة
-
- \(\frac{2}{3}\)
- \(\frac{4}{5}\)
- \(\frac{1}{2}\)
تذكر أن الكسر يتم تبسيطه عندما لا يحتوي على عوامل مشتركة، بخلاف 1، في البسط والمقام. عندما نقيم تعبيرًا منطقيًا، نتأكد من تبسيط الكسر الناتج.
قم\(\frac{a^2+2ab+b^2}{3ab}\) بالتقييم لكل قيمة.
- أ=1، ب = 2
- a=−2، b=−1
- \(a=\frac{1}{3}\)، ب = 0
الحل
| 1. | \(\frac{a^2+2ab+b^2}{3ab}\)عندما a = 1، b = 2 |
 |
 |
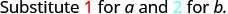| قم بالتبسيط. |  |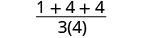
 |
|
 |
|
| 2. | \(\frac{a^2+2ab+b^2}{3ab}\)عندما a=−2، b=−1 |
 |
 |
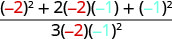| قم بالتبسيط. |  |
 |
|
 |
|
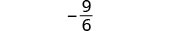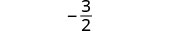| 3. | \(\frac{a^2+2ab+b^2}{3ab}\)عندما\(a=\frac{1}{3}\)، ب = 0 |
 |
 |
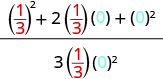| قم بالتبسيط. |  |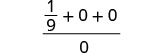
 |
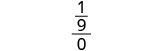جرب ذلك\(\PageIndex{11}\)
تقييم\(\frac{2a^{3}b}{a^2+2ab+b^2}\) for each value.
- a=−1, b=2
- a=0, b=−1
- a=1, \(b=\frac{1}{2}\)
- Answer
-
- −4
- 0
- \(\frac{4}{9}\)
Try It \(\PageIndex{12}\)
قم\(\frac{a^2−b^2}{8ab^3}\) بالتقييم لكل قيمة:
- أ=1، ب = −1
- \(a=\frac{1}{2}\)، ب = −1
- أ=−2، ب = 1
- إجابة
-
- 0
- \(\frac{3}{16}\)
- \(\frac{3}{16}\)
تبسيط التعبيرات الكسرية
تمامًا مثل الكسر يُعتبر مبسطًا إذا لم تكن هناك عوامل مشتركة، بخلاف 1، في البسط والمقام، يتم تبسيط التعبير العقلاني إذا لم يكن له عوامل مشتركة، بخلاف 1، في البسط والمقام.
يعتبر التعبير العقلاني مبسطًا إذا لم تكن هناك عوامل مشتركة في البسط والمقام.
على سبيل المثال:
- \(\frac{2}{3}\)تم تبسيطه نظرًا لعدم وجود عوامل مشتركة لـ 2 و 3.
- \(\frac{2x}{3x}\)لم يتم تبسيطه لأن x هو عامل مشترك لـ 2 x و 3 x.
نحن نستخدم خاصية الكسور المتكافئة لتبسيط الكسور العددية. نعيد ذكرها هنا حيث سنستخدمها أيضًا لتبسيط التعبيرات العقلانية.
إذا كانت a و b و c عبارة عن أرقام حيث\(b \ne 0\)\(c\ne 0\)، ثم\(\frac{a}{b}=\frac{a·c}{b·c}\) و\(\frac{a·c}{b·c}=\frac{a}{b}\)
لاحظ أنه في خاصية الكسور المتكافئة، لا يُسمح على وجه التحديد بالقيم التي تجعل المقامات صفرًا. نرى\(b \ne 0\)، مذكور\(c\ne 0\) بوضوح. في كل مرة نكتب فيها تعبيرًا منطقيًا، يجب أن نصدر بيانًا مشابهًا يمنع القيم التي تجعل المقام صفرًا. ومع ذلك، دعونا نركز على العمل المطروح، سنحذف كتابته في الأمثلة.
لنبدأ بمراجعة كيفية تبسيط الكسور العددية.
قم بالتبسيط:\(−\frac{36}{63}\).
الحل
 |
|
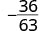| أعد كتابة البسط والمقام لتوضيح العوامل المشتركة. |  |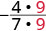
| قم بالتبسيط باستخدام خاصية الكسور المتكافئة. |  |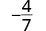
لاحظ أن الكسر\(−\frac{4}{7}\) مبسط لأنه لا توجد عوامل أكثر شيوعًا.
جرب ذلك\(\PageIndex{14}\)
قم بالتبسيط:\(−\frac{45}{81}\).
- Answer
-
\(−\frac{5}{9}\)
Try It \(\PageIndex{15}\)
قم بالتبسيط:\(−\frac{42}{54}\).
- إجابة
-
\(−\frac{7}{9}\)
خلال هذا الفصل، سنفترض أنه تم استبعاد جميع القيم العددية التي تجعل المقام صفرًا. لن نكتب القيود لكل تعبير عقلاني، ولكن ضع في اعتبارك أن المقام لا يمكن أن يكون صفرًا أبدًا. لذلك في هذا المثال التالي،\(x \ne 0\) و\(y \ne 0\).
قم بالتبسيط:\(\frac{3xy}{18x^{2}y^{2}}\).
الحل
 |
|
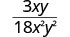| أعد كتابة البسط والمقام لتوضيح العوامل المشتركة. |  |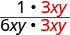
| قم بالتبسيط باستخدام خاصية الكسور المتكافئة. |  |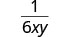
هل لاحظت أن هذه هي نفس الخطوات التي اتخذناها عندما قسمنا وحيدات الحدود في كثيرات الحدود؟
جرب ذلك\(\PageIndex{17}\)
قم بالتبسيط:\(\frac{4x^{2}y}{12xy^2}\).
- Answer
-
\(\frac{x}{3y}\)
Try It \(PageIndex{18}\)
قم بالتبسيط:\(\frac{16x^{2}y}{2xy^2}\).
- إجابة
-
\(\frac{8x}{y}\)
كن حذرًا جدًا أثناء إزالة العوامل المشتركة. يتم ضرب العوامل لصنع منتج. يمكنك إزالة عامل من المنتج. لا يمكنك إزالة مصطلح من المجموع.
لاحظ أن إزالة x من\(\frac{x+5}{x}\) ستكون مثل إلغاء 2 في الكسر\(\frac{2+5}{2}\)!
كيفية تبسيط المقادير النسبية ذات الحدين
قم بالتبسيط:\(\frac{2x+8}{5x+20}\).
الحل
جرب ذلك\(\PageIndex{20}\)
قم بالتبسيط:\(\frac{3x−6}{2x−4}\).
- Answer
-
\(\frac{3}{2}\)
Try It \(\PageIndex{21}\)
قم بالتبسيط:\(\frac{7y+35}{5y+25}\).
- إجابة
-
\(\frac{7}{5}\)
نلخص الآن الخطوات التي يجب اتباعها لتبسيط التعبيرات العقلانية.
- ضع البسط والمقام في الاعتبار تمامًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
سنستخدم الطرق التي تناولناها في التحليل لتحليل كثيرات الحدود في البسط والمقامات في الأمثلة التالية.
قم بالتبسيط:\(\frac{x^2+5x+6}{x^2+8x+12}\).
الحل
| \(\frac{x^2+5x+6}{x^2+8x+12}\) | |
| عامل البسط والمقام. | \(\frac{(x+2)(x+3)}{(x+2)(x+6)}\) |
| أزل العامل المشترك x+2 من البسط والمقام. | \(\frac{x+3}{x+6}\) |
هل يمكنك معرفة قيم x التي يجب استبعادها في هذا المثال؟
جرب ذلك\(\PageIndex{23}\)
قم بالتبسيط:\(\frac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\frac{x+1}{x−1}\)
Try It \(\PageIndex{24}\)
قم بالتبسيط:\(\frac{x^2−3x−10}{x^2+x−2}\).
- إجابة
-
\(\frac{x−5}{x−1}\)
قم بالتبسيط:\(\frac{y^2+y−42}{y^2−36}\).
الحل
| \(\frac{y^2+y−42}{y^2−36}\). | |
| عامل البسط والمقام. | \(\frac{(y+7)(y−6)}{(y+6)(y−6)}\) |
| أزل العامل المشترك y−6 من البسط والمقام. | \(\frac{y+7}{y+6}\) |
جرب ذلك\(\PageIndex{26}\)
قم بالتبسيط:\(\frac{x^2+x−6}{x^2−4}\).
- Answer
-
\(\frac{x+3}{x+2}\)
Try It \(\PageIndex{27}\)
قم بالتبسيط:\(\frac{x^2+8x+7}{x^2−49}\).
- إجابة
-
\(\frac{x+1}{x−7}\)
قم بالتبسيط:\(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\).
الحل
| \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\) | |
| عامِل البسط والمقام باستخدام التجميع لحساب البسط. | \(\frac{p^2(p−2)+2(p−2)}{(p−5)(p−2)}\) |
| \(\frac{(p^2+2)(p−2)}{(p−5)(p−2)}\) | |
| أزل العامل المشترك p−2 من البسط والمقام. | \(\frac{p^2+2}{p−5}\) |
جرب ذلك\(\PageIndex{29}\)
قم بالتبسيط:\(\frac{y^3−3y^2+y−3}{y^2−y−6}\).
- Answer
-
\(\frac{y^2+1}{y+2}\)
Try It \(\PageIndex{30}\)
قم بالتبسيط:\(\frac{p^3−p^2+2p−2}{p^2+4p−5}\).
- إجابة
-
\(\frac{p^2+2}{p+5}\)
قم بالتبسيط:\(\frac{2n^2−14n}{4n^2−16n−48}\).
الحل
| \(\frac{2n^2−14n}{4n^2−16n−48}\) | |
| ضع البسط والمقام في الاعتبار، مع استبعاد عامل GCF أولاً. | \(\frac{2n(n−7)}{4(n^2−4n−12)}\) |
| \(\frac{2n(n−7)}{4(n−6)(n+2)}\) | |
| قم بإزالة العامل المشترك، 2. | \(\frac{n(n−7)}{2(n−6)(n+2)}\) |
جرب ذلك\(\PageIndex{32}\)
قم بالتبسيط:\(\frac{2n^2−10n}{4n^2−16n−20}\).
- Answer
-
\(\frac{n}{2(n+1)}\)
Try It \(\PageIndex{33}\)
قم بالتبسيط:\(\frac{4x^2−16x}{8x^2−16x−64}\).
- إجابة
-
\(\frac{x}{2(x+2)}\)
قم بالتبسيط:\(\frac{3b^2−12b+12}{6b^2−24}\).
الحل
| \(\frac{3b^2−12b+12}{6b^2−24}\) | |
| ضع البسط والمقام في الاعتبار، مع استبعاد عامل GCF أولاً. | \(\frac{3(b^2−4b+4)}{6(b^2−4)}\) |
| \(\frac{3(b−2)(b−2)}{6(b−2)(b+2)}\) | |
| أزل العوامل المشتركة لـ b−2 و3. | \(\frac{3(b−2)}{2(b+2)}\) |
جرب ذلك\(\PageIndex{35}\)
قم بالتبسيط:\(\frac{2x^2−12x+18}{3x^2−27}\).
- Answer
-
\(\frac{2(x−3)}{3(x+3)}\)
Try It \(PageIndex{36}\)
قم بالتبسيط:\(\frac{5y^2−30y+25}{2y^2−50}\).
- إجابة
-
\(\frac{5(x−1)}{2(x+5)}\)
قم بالتبسيط:\(\frac{m^3+8}{m^2−4}\).
الحل
| \(\frac{m^3+8}{m^2−4}\) | |
| عامِل البسط والمقام باستخدام معادلات مجموع المكعبات والفرق بين المربعات. | \(\frac{(m+2)(m^2−2m+4)}{(m+2)(m−2)}\) |
| قم بإزالة العوامل المشتركة لـ m+2. | \(\frac{m^2−2m+4}{m−2}\) |
جرب ذلك\(\PageIndex{38}\)
قم بالتبسيط:\(\frac{p^3−64}{p^2−16}\).
- Answer
-
\(\frac{p^2+4p+16}{p+4}\)
Try It \(\PageIndex{39}\)
قم بالتبسيط:\(\frac{x^3+8}{x^2−4}\).
- إجابة
-
\(\frac{x^2−2x+4}{x−2}\)
تبسيط التعبيرات الكسرية باستخدام العوامل المعاكسة
سنرى الآن كيفية تبسيط التعبير العقلاني الذي يحتوي البسط والمقام على عوامل معاكسة. لنبدأ بكسر عددي، على سبيل المثال\(\frac{7}{−7}\).
نحن نعلم أن هذا الكسر يتبسط إلى −1. نحن ندرك أيضًا أن البسط والمقام متضادان.
في كتاب التأسيس، أدخلنا رمزاً معاكسًا: نقيض a هو −a، ونتذكر أيضًا أن −a=−1·a
نحن نبسط الكسر\(\frac{a}{−a}\)
\[\begin{array}{ll} {}&{\frac{a}{−a}}\\ {\text{We could rewrite this.}}&{\frac{1·a}{−1·a}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
لذلك، بنفس الطريقة، يمكننا تبسيط الكسر\(\frac{x−3}{−(x−3)}\)
\[\begin{array}{ll} {}&{\frac{x−3}{−(x−3)}}\\ {\text{We could rewrite this.}}&{\frac{1·(x−3)}{−1·(x−3)}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
ولكن يمكن كتابة عكس x−3 بشكل مختلف:
\[\begin{array}{ll} {}&{−(x−3)}\\ {\text{Distribute.}}&{−x+3}\\ {\text{Rewrite.}}&{3−x}\\ \nonumber \end{array}\]
وهذا يعني\(\frac{x−3}{3−x}\) تبسيط الكسر إلى −1.
وبشكل عام، يمكننا كتابة عكس a−b في صورة b−a، وبذلك يتم\(\frac{a−b}{b−a}\) تبسيط التعبير العقلاني إلى −1.
نقيض a−b هو b−a
\(\frac{a−b}{b−a}=−1\)،\(a \ne b\)
تعبير وقسمته المعاكسة لـ −1
سنستخدم هذه الخاصية لتبسيط التعبيرات العقلانية التي تحتوي على أضداد في البسط والمقامات.
قم بالتبسيط:\(\frac{x−8}{8−x}\).
الحل
| \(\frac{x−8}{8−x}\). | |
| اعلم أن x−8 و8−x هما أضداد | −1 |
جرب ذلك\(\PageIndex{41}\)
قم بالتبسيط:\(\frac{y−2}{2−y}\).
- Answer
-
−1
Try It \(\PageIndex{42}\)
قم بالتبسيط:\(\frac{n−9}{9−n}\).
- إجابة
-
−1
تذكر أن الخطوة الأولى في تبسيط التعبير العقلاني هي حساب البسط والمقام بالكامل.
قم بالتبسيط:\(\frac{14−2x}{x^2−49}\).
الحل
 |
|
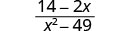| عامل البسط والمقام. |  |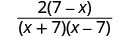
| تعرف على أن 7−x وx−7 أضداد. |  |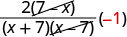
| قم بالتبسيط. |  |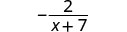
جرب ذلك\(\PageIndex{44}\)
قم بالتبسيط:\(\frac{10−2y}{y^2−25}\).
- Answer
-
\(−\frac{2}{y+5}\)
Try It \(\PageIndex{45}\)
قم بالتبسيط:\(\frac{3y−27}{81−y^2}\).
- إجابة
-
\(−\frac{3}{9+y}\)
قم بالتبسيط:\(\frac{x^2−4x−32}{64−x^2}\).
الحل
 |
|
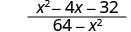| عامل البسط والمقام. |  |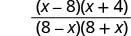
| تعرف على العوامل المضادة. |  |
| قم بالتبسيط. |  |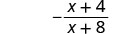
جرب ذلك\(\PageIndex{47}\)
قم بالتبسيط:\(\frac{x^2−4x−5}{25−x^2}\).
- Answer
-
\(−\frac{x+1}{x+5}\)
Try It \(\PageIndex{48}\)
قم بالتبسيط:\(\frac{x^2+x−2}{1−x^2}\).
- إجابة
-
\(−\frac{x+2}{x+1}\)
المفاهيم الرئيسية
- حدد القيم التي لا يتم تعريف التعبير العقلاني لها
- عيّن المقام مساويًا للصفر.
- حل المعادلة، إن أمكن.
- تعبير عقلاني مبسط
- يعتبر التعبير العقلاني مبسطًا إذا لم تكن هناك عوامل مشتركة في البسط والمقام.
- تبسيط التعبير العقلاني
- ضع البسط والمقام في الاعتبار تمامًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
- الأضداد في تعبير عقلاني
- نقيض a−b هو b−a
\(\frac{a−b}{b−a}=−1\)\(a \ne b\)،\(b \ne 0\)،\(a \ne b\)
- نقيض a−b هو b−a
الممارسة تجعل من الكمال
في التمارين التالية، حدد القيم التي لم يتم تعريف التعبير العقلاني لها.
- \(\frac{2x}{z}\)
- \(\frac{4p−1}{6p−5}\)
- \(\frac{n−3}{n^2+2n−8}\)
- إجابة
-
- ض = 0
- \(p=\frac{5}{6}\)
- ن=−4، ن = 2
- \(\frac{10m}{11n}\)
- \(\frac{6y+13}{4y−9}\)
- \(\frac{b−8}{b^2−36}\)
- \(\frac{4x^{2}y}{3y}\)
- \(\frac{3x−2}{2x+1}\)
- \(\frac{u−1}{u^2−3u−28}\)
- إجابة
-
- ص = 0
- \(x=−\frac{1}{2}\)
- u=−4، u=7
- \(\frac{5pq^{2}}{9q}\)
- \(\frac{7a−4}{3a+5}\)
- \(\frac{1}{x^2−4}\)
في التمارين التالية، قم بتقييم التعبير العقلاني للقيم المُعطاة.
\(\frac{2x}{x−1}\)
- س = 0
- س = 2
- x=−1
- إجابة
-
- 0
- 4
- 1
\(\frac{4y−1}{5y−3}\)
- ص = 0
- ص = 2
- y=−1
\(\frac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=−2
- إجابة
-
- 3
- \(\frac{5}{2}\)
- \(−\frac{1}{5}\)
\(\frac{x+3}{2−3x}\)
- س = 0
- س = 1
- x=−2
\(\frac{y^2+5y+6}{y^2−1}\)
- ص = 0
- ص = 2
- y=−2
- إجابة
-
- −6
- \(\frac{20}{3}\)
- 0
\(\frac{z^2+3z−10}{z^2−1}\)
- ض = 0
- z = 2
- z=−2
\(\frac{a^2−4}{a^2+5a+4}\)
- أ=0
- أ=1
- a=−2
- إجابة
-
- −1
- \(−\frac{3}{10}\)
- 0
\(\frac{b^2+2}{b^2−3b−4}\)
- ب = 0
- ب = 2
- ب = −2
\(\frac{x^2+3xy+2y^2}{2x^{3}y}\)
- س = 1، ص = −1
- س = 2، ص = 1
- x=−1، y=−2
- إجابة
-
- 0
- \(\frac{3}{4}\)
- \(\frac{15}{4}\)
\(\frac{c^2+cd−2d^2}{cd^{3}}\)
- c=2، d=−1
- c=1، d=−1
- c=−1، d=2
\(\frac{m^2−4n^2}{5mn^3}\)
- م = 2، ن = 1
- m=−1، n=−1
- م = 3، ن = 2
- إجابة
-
- 0
- \(−\frac{3}{5}\)
- \(−\frac{7}{20}\)
\(\frac{2s^{2}t}{s^2−9t^2}\)
- s=4، t=1
- s=−1، t=−1
- s=0، t=2
في التمارين التالية، قم بالتبسيط.
\(−\frac{4}{52}\)
- إجابة
-
\(−\frac{1}{13}\)
\(−\frac{44}{55}\)
\(\frac{56}{63}\)
- إجابة
-
\(\frac{8}{9}\)
\(\frac{65}{104}\)
\(\frac{6ab^{2}}{12a^{2}b}\)
- إجابة
-
\(\frac{b}{2ab}\)
\(\frac{15xy^{3}}{x^{3}y^{3}}\)
\(\frac{8m^{3}n}{12mn^2}\)
- إجابة
-
\(\frac{2m^2}{3n}\)
\(\frac{36v^{3}w^2}{27vw^3}\)
\(\frac{3a+6}{4a+8}\)
- إجابة
-
\(\frac{3}{4}\)
\(\frac{5b+5}{6b+6}\)
\(\frac{3c−9}{5c−15}\)
- إجابة
-
\(\frac{3}{5}\)
\(\frac{4d+8}{9d+18}\)
\(\frac{7m+63}{5m+45}\)
- إجابة
-
\(\frac{7}{5}\)
\(\frac{8n−96}{3n−36}\)
\(\frac{12p−240}{5p−100}\)
- إجابة
-
\(\frac{12}{5}\)
\(\frac{6q+210}{5q+175}\)
\(\frac{a^2−a−12}{a^2−8a+16}\)
- إجابة
-
\(\frac{a+3}{a−4}\)
\(\frac{x^2+4x−5}{x^2−2x+1}\)
\(\frac{y^2+3y−4}{y^2−6y+5}\)
- إجابة
-
\(\frac{y+4}{y−5}\)
\(\frac{v^2+8v+15}{v^2−v−12}\)
\(\frac{x^2−25}{x^2+2x−15}\)
- إجابة
-
\(\frac{x−5}{x−3}\)
\(\frac{a^2−4}{a^2+6a−16}\)
\(\frac{y^2−2y−3}{y^2−9}\)
- إجابة
-
\(\frac{y+1}{y+3}\)
\(\frac{b^2+9b+18}{b^2−36}\)
\(\frac{y^3+y^2+y+1}{y^2+2y+1}\)
- إجابة
-
\(\frac{y^2+1}{y+1}\)
\(\frac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\frac{x^3−2x^2−25x+50}{x^2−25}\)
- إجابة
-
x−2
\(\frac{q^3+3q^2−4q−12}{q^2−4}\)
\(\frac{3a^2+15a}{6a^2+6a−36}\)
- إجابة
-
\(\frac{a(a+5)}{2(a+3)(a−2)}\)
\(\frac{8b^2−32b}{2b^2−6b−80}\)
\(\frac{−5c^2−10c}{−10c^2+30c+100}\)
- إجابة
-
\(\frac{c}{2(c−5)}\)
\(\frac{4d^2−24d}{2d^2−4d−48}\)
\(\frac{3m^2+30m+75}{4m^2−100}\)
- إجابة
-
\(\frac{3(m+5)}{4(m−5)}\)
\(\frac{5n^2+30n+45}{2n^2−18}\)
\(\frac{5r^2+30r−35}{r^2−49}\)
- إجابة
-
\(\frac{5(r−1)}{r+7}\)
\(\frac{3s^2+30s+24}{3s^2−48}\)
\(\frac{t^3−27}{t^2−9}\)
- إجابة
-
\(\frac{t^2+3t+9}{t+3}\)
\(\frac{v^3−1}{v^2−1}\)
\(\frac{w^3+216}{w^2−36}\)
- إجابة
-
\(\frac{w^2−6w+36}{w−6}\)
\(\frac{v^3+125}{v^2−25}\)
تبسيط التعبيرات الكسرية باستخدام العوامل المعاكسة
في التمارين التالية، قم بتبسيط كل تعبير عقلاني.
\(\frac{a−5}{5−a}\)
- إجابة
-
−1
\(\frac{b−12}{12−b}\)
\(\frac{11−c}{c−11}\)
- إجابة
-
−1
\(\frac{5−d}{d−5}\)
\(\frac{12−2x}{x^2−36}\)
- إجابة
-
\(−\frac{2}{x+6}\)
\(\frac{20−5y}{y^2−16}\)
\(\frac{4v−32}{64−v^2}\)
- إجابة
-
\(−\frac{4}{8+v}\)
\(\frac{7w−21}{9−w^2}\)
\(\frac{y^2−11y+24}{9−y^2}\)
- إجابة
-
\(−\frac{y−8}{3+y}\)
\(\frac{z^2−9z+20}{16−z^2}\)
\(\frac{a^2−5a−36}{81−a^2}\)
- إجابة
-
\(−\frac{a+4}{9+a}\)
\(\frac{b^2+b−42}{36−b^2}\)
الرياضيات اليومية
معدلات الضرائب بالنسبة للسنة الضريبية 2015، يمكن العثور على مبلغ الضريبة المستحقة على شخص واحد يكسب ما بين 37,450 دولارًا و 90,750 دولارًا، من خلال تقييم الصيغة 0.25x−4206.25، حيث x هي الدخل. يمكن العثور على متوسط معدل الضريبة لهذا الدخل من خلال تقييم الصيغة\(\frac{0.25x−4206.25}{x}\). ما هو متوسط معدل الضريبة لشخص واحد يكسب 50,000 دولار؟
- إجابة
-
16.5%
العمل يمكن العثور على طول الوقت الذي يستغرقه شخصان لأداء نفس المهمة إذا عملوا معًا من خلال تقييم الصيغة\(\frac{xy}{x+y}\). إذا كان توم قادرًا على طلاء العرين في x=45 دقيقة وكان بإمكان شقيقه بوبي رسمه في y=60 دقيقة، فما عدد الدقائق التي سيستغرقها العمل معًا؟
تمارين الكتابة
اشرح كيفية العثور على قيم x التي لم\(\frac{x^2−x−20}{x^2−4}\) يتم تعريف التعبير العقلاني لها.
اشرح جميع الخطوات التي تتخذها لتبسيط التعبير العقلاني\(\frac{p^2+4p−21}{9−p^2}\).
فحص ذاتي
ⓐ بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم إتقانك لأهداف هذا القسم.
ⓑ إذا كانت معظم الشيكات الخاصة بك:
... بثقة. تهانينا! لقد حققت أهدافك في هذا القسم! فكر في مهارات الدراسة التي استخدمتها حتى تتمكن من الاستمرار في استخدامها. ماذا فعلت لتصبح واثقًا من قدرتك على القيام بهذه الأشياء؟ كن محددًا!
... مع بعض المساعدة. يجب معالجة هذا بسرعة لأن الموضوعات التي لا تتقنها تصبح ثقوبًا في طريقك إلى النجاح. الرياضيات متسلسلة - كل موضوع يعتمد على العمل السابق. من المهم التأكد من أن لديك أساسًا قويًا قبل المضي قدمًا. من الذي يمكنك طلب المساعدة؟ يعتبر زملائك في الفصل والمدرب موارد جيدة. هل يوجد مكان في الحرم الجامعي حيث يتوفر مدرسو الرياضيات؟ هل يمكن تحسين مهاراتك الدراسية؟
... لا - أنا لا أفهم ذلك! هذا أمر بالغ الأهمية ويجب ألا تتجاهله. تحتاج إلى الحصول على المساعدة على الفور وإلا ستصاب بالارتباك بسرعة. راجع مدرسك في أقرب وقت ممكن لمناقشة وضعك. معًا يمكنك وضع خطة للحصول على المساعدة التي تحتاجها.
مسرد المصطلحات
- تعبير عقلاني
- التعبير العقلاني هو تعبير عن الشكل\(\frac{p}{q}\)، حيث p و q هما كثيرات الحدود و\(q \ne 0\).