7.3: معامِل التثليث التربيعي ذات المعامل الرئيسي غير 1
- Page ID
- 200200
في نهاية هذا القسم، ستكون قادرًا على:
- تعرف على الإستراتيجية الأولية لحساب كثيرات الحدود تمامًا
- العوامل الثلاثية للنموذج\(ax^{2}+bx+c\) مع GCF
- معاملات ثلاثية الحدود باستخدام التجربة والخطأ
- عوامل ثلاثية الحدود باستخدام طريقة «ac»
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- ابحث عن GCF لـ 45\(p^{2}\) و 30\(p^{6}\)
إذا فاتتك هذه المشكلة، راجع التمرين 7.1.4. - اضرب\((3 y+4)(2 y+5)\)
إذا فاتتك هذه المشكلة، راجع التمرين 6.3.37. - اجمع بين المصطلحات المتشابهة\(12 x^{2}+3 x+5 x+9\)
إذا فاتتك هذه المشكلة، راجع التمرين 1.3.37.
التعرف على الإستراتيجية الأولية للتخصيم
دعونا نلخص ما وصلنا إليه حتى الآن من خلال تحليل كثيرات الحدود. في القسمين الأولين من هذا الفصل، استخدمنا ثلاث طرق للعوملة: تحليل GCF، والعوملة حسب التجميع، وعوملة ثلاثية الحدود عن طريق «التراجع» عن FOIL. ستتبع المزيد من الأساليب أثناء المتابعة في هذا الفصل، وكذلك لاحقًا في دراساتك للجبر.
كيف ستعرف متى تستخدم كل طريقة من طرق التخصيم؟ عندما تتعلم المزيد من طرق التخصيم، كيف ستعرف متى يجب تطبيق كل طريقة وعدم الخلط بينها؟ سيساعدك ذلك على تنظيم طرق العوملة في إستراتيجية يمكنها إرشادك لاستخدام الطريقة الصحيحة.
عندما تبدأ في حساب كثير الحدود، اسأل دائمًا أولاً، «هل هناك عامل مشترك أكبر؟» إذا كان هناك، فقم بأخذه في الاعتبار أولاً.
الشيء التالي الذي يجب مراعاته هو نوع متعدد الحدود. كم عدد المصطلحات الموجودة بها؟ هل هي معادلة ذات حدين؟ معادلة ثلاثية؟ أم أنها تحتوي على أكثر من ثلاثة فصول؟
- إذا كانت المعادلة ثلاثية حيث يكون المعامل الرئيسي واحدًا\(x^{2}+b x+c\)، فاستخدم طريقة «التراجع عن FOIL».
- إذا كانت تحتوي على أكثر من ثلاثة مصطلحات، فجرّب طريقة التجميع. هذه هي الطريقة الوحيدة المستخدمة لكثيرات الحدود التي تزيد عن ثلاثة مصطلحات.
لا يمكن أخذ بعض كثيرات الحدود في الاعتبار. يطلق عليهم اسم «برايم». فيما يلي نلخص الأساليب التي لدينا حتى الآن.
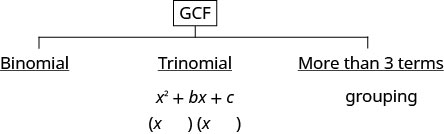
- هل هناك عامل مشترك أكبر؟
- ضع في اعتبارك ذلك.
- هل كثير الحدود عبارة عن معادلة ذات حدين أو ثلاثية أو أكثر من ثلاثة حدود؟
- إذا كانت ذات حدين، فليس لدينا الآن طريقة لأخذها في الاعتبار.
- إذا كانت عبارة عن ثلاثية الأبعاد للنموذج\(x^{2}+b x+c\): Undo FOIL\((x\qquad)(x\qquad)\)
- إذا كان يحتوي على أكثر من ثلاثة مصطلحات: استخدم طريقة التجميع.
- تحقق من ذلك بضرب العوامل.
استخدم الإستراتيجية الأولية لتحليل كثير الحدود بالكامل. يتم أخذ كثير الحدود في الاعتبار تمامًا إذا كانت جميع عوامله أولية، بخلاف القيم الأحادية.
حدد أفضل طريقة لاستخدامها في حساب كل كثير الحدود.
- \(6 y^{2}-72\)
- \(r^{2}-10 r-24\)
- \(p^{2}+5 p+p q+5 q\)
- الإجابة أ
-
\[\begin{array}{ll} &6 y^{2}-72\\ \text { Is there a greatest common factor? } & \text {Yes, 6. } \\ \text { Factor out the } 6 &6\left(y^{2}-12\right) \\ \text { Is it a binomial, trinomial, or are there } & \text {Binomial, we have no method to factor } \\ \text { more than } 3 \text { terms? } & \text {binomials yet. } \end{array} \nonumber\]
- الإجابة ب
-
\[\begin{array}{ll} &r^{2}-10 r-24\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {Trinomial, with leading coefficient } 1, \text { so } \\ \text { more than three terms? }& \text {"undo" FOIL. }\end{array} \nonumber\]
- الإجابة ج
-
\[\begin{array}{ll} &p^{2}+5 p+p q+5 q\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {More than three terms, so factor using }\\ \text { more than three terms? }& \text {grouping. }\end{array} \nonumber\]
حدد أفضل طريقة لاستخدامها في تحليل كل كثير الحدود:
- \(4 y^{2}+32\)
- \(y^{2}+10 y+21\)
- \(y z+2 y+3 z+6\)
- الإجابة أ
-
لا توجد طريقة
- الإجابة ب
-
التراجع عن استخدام FOIL
- الإجابة ج
-
عامل مع التجميع
حدد أفضل طريقة لاستخدامها في تحليل كل كثير الحدود:
- \(a b+a+4 b+4\)
- \(3 k^{2}+15\)
- \(p^{2}+9 p+8\)
- الإجابة أ
-
عامل باستخدام التجميع
- الإجابة ب
-
لا توجد طريقة
- الإجابة ج
-
التراجع عن استخدام FOIL
العوامل الثلاثية للنموذج بحد أقصى 2 + مربع+x x مع GCF
الآن بعد أن قمنا بتنظيم ما قمنا بتغطيته حتى الآن، نحن على استعداد لتحليل التثليفات الثلاثية التي لا يكون معاملها الرئيسي 1، وهي ثلاثية الحدود للشكل\(a x^{2}+b x+c\). تذكر دائمًا التحقق من GCF أولاً! في بعض الأحيان، بعد حساب GCF، يصبح المعامل الرئيسي للثلاثي الحدود 1 ويمكنك حسابه بالطرق الموجودة في القسم الأخير. لنقم ببعض الأمثلة لنرى كيف يعمل هذا. احترس من العلامات في المثالين التاليين.
عامل بالكامل:\(2 n^{2}-8 n-42\).
- إجابة
-
استخدم الإستراتيجية الأولية.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&2 n^{2}-8 n-42\\ \text { Yes, GCF }=2 . \text { Factor it out. }& 2\left(n^{2}-4 n-21\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 2(n\qquad )(n\qquad) \\ \text { Use } 3 \text { and }-7 \text { as the last terms of the binomials. } & 2(n+3)(n-7) \end{array}\)
عوامل −21 مجموع العوامل 1، −21 1+ (−21) = −20 3، −7 3+ (−7) =−4* \(\begin{array}{l}{\text {Check. }} \\ {2(n+3)(n-7)} \\ {2\left(n^{2}-7 n+3 n-21\right)} \\ {2\left(n^{2}-4 n-21\right)} \\ {2 n^{2}-8 n-42 }\checkmark \end{array}\)
عامل بالكامل:\(4 m^{2}-4 m-8\)
- إجابة
-
4\((m+1)(m-2)\)
عامل بالكامل:\(5 k^{2}-15 k-50\)
- إجابة
-
5\((k+2)(k-5)\)
عامل بالكامل:\(4 y^{2}-36 y+56\)
- إجابة
-
استخدم الإستراتيجية الأولية.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 y^{2}-36 y+56\\ \text { Yes, GCF }=4 . \text { Factor it out. }&4\left(y^{2}-9 y+14\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 4(y\qquad )(y\qquad) \\\text { Use a table like the one below to find two numbers that multiply to }&\\ 14 \text { and add to }-9\\ \text { Both factors of } 14 \text { must be negative. } & 4(y-2)(y-7) \end{array}\)عوامل 14 مجموع العوامل −1، −14 −1+ (−14) =−15 −2، −7 −2+ (−7) =−9* \(\begin{array}{l}{\text { Check. }} \\ {4(y-2)(y-7)} \\ {4\left(y^{2}-7 y-2 y+14\right)} \\ {4\left(y^{2}-9 y+14\right)} \\ {4 y^{2}-36 y+42 } \checkmark \end{array}\)
عامل بالكامل:\(3 r^{2}-9 r+6\)
- إجابة
-
3\((r-1)(r-2)\)
عامل بالكامل:\(2 t^{2}-10 t+12\)
- إجابة
-
2\((t-2)(t-3)\)
في المثال التالي، سيتضمن GCF متغيرًا.
عامل بالكامل:\(4 u^{3}+16 u^{2}-20 u\)
- إجابة
-
استخدم الإستراتيجية الأولية.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 u^{3}+16 u^{2}-20 u\\ \text { Yes, GCF }=4 u . \text { Factor it. }&4 u\left(u^{2}+4 u-5\right) \\\text { Binomial, trinomial, or more than three terms? }&\\ \text { more than three terms? }& \\ \text { It is a trinomial. So "undo FOIL." } & 4u(u\qquad )(u\qquad) \\\text { Use a table like the table below to find two numbers that }&4 u(u-1)(u+5)\\ \text { multiply to }-5 \text { and add to } 4\end{array}\)عوامل −5 مجموع العوامل −1,5 −1+5=4* 1، −5 1+ (−5) =−4 تحقق.
\(\begin{array}{l}{4 u(u-1)(u+5)} \\ {4 u\left(u^{2}+5 u-u-5\right)} \\ {4 u\left(u^{2}+4 u-5\right)} \\ {4 u^{3}+16 u^{2}-20 u }\checkmark \end{array}\)
عامل بالكامل:\(5 x^{3}+15 x^{2}-20 x\)
- إجابة
-
5\(x(x-1)(x+4)\)
عامل بالكامل:\(6 y^{3}+18 y^{2}-60 y\)
- إجابة
-
6\(y(y-2)(y+5)\)
معاملات ثلاثية الحدود باستخدام التجربة والخطأ
ماذا يحدث عندما لا يكون المعامل الرئيسي 1 ولا يوجد GCF؟ هناك العديد من الطرق التي يمكن استخدامها لتحليل هذه القيم الثلاثية. أولاً سنستخدم طريقة التجربة والخطأ.
دعونا نأخذ في الاعتبار الثلاثي\(3 x^{2}+5 x+2\)
نتوقع من عملنا السابق أن يتحول هذا إلى حدين.
\[\begin{array}{c}{3 x^{2}+5 x+2} \\ {( \qquad)( \qquad)}\end{array}\]
نحن نعلم أن المصطلحات الأولى من العوامل ذات الحدين ستتضاعف لتعطينا 3\(x^{2}\). العوامل الوحيدة لـ 3\(x^{2}\) هي\(1 x, 3 x\). يمكننا وضعها في الحدود الثنائية.
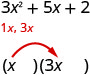
تحقق. هل\(1 x \cdot 3 x=3 x^{2}\)؟
نحن نعلم أن المصطلحات الأخيرة من الحدين ستضرب في 2. نظرًا لأن هذه العبارة الثلاثية تحتوي على جميع المصطلحات الإيجابية، فإننا نحتاج فقط إلى النظر في العوامل الإيجابية. العوامل الوحيدة لـ 2 هي 1 و 2. ولكن لدينا الآن حالتان يجب مراعاتهما حيث ستحدث فرقًا إذا كتبنا 1 أو 2 أو 2 أو 1.

ما هي العوامل الصحيحة؟ لنقرر ذلك، نضرب المصطلحات الداخلية والخارجية.
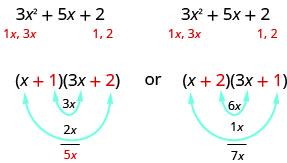
نظرًا لأن المدى المتوسط للثلاثية هو 5 x، فإن العوامل في الحالة الأولى ستعمل. دعنا نفحص الأمر.
\[\begin{array}{l}{(x+1)(3 x+2)} \\ {3 x^{2}+2 x+3 x+2} \\ {3 x^{2}+5 x+2}\checkmark \end{array}\]
نتيجة التخصيم لدينا هي:
\[\begin{array}{l}{3 x^{2}+5 x+2} \\ {(x+1)(3 x+2)}\end{array}\]
عامل بالكامل:\(3 y^{2}+22 y+7\)
- إجابة
-





عامل بالكامل:\(2 a^{2}+5 a+3\)
- إجابة
-
\((a+1)(2 a+3)\)
عامل بالكامل:\(4 b^{2}+5 b+1\)
- إجابة
-
\((b+1)(4 b+1)\)
- اكتب ثلاثية الحدود بترتيب تنازلي للدرجات.
- ابحث عن جميع أزواج عوامل الحد الأول.
- ابحث عن جميع أزواج عوامل الحد الثالث.
- اختبر جميع المجموعات الممكنة من العوامل حتى يتم العثور على المنتج الصحيح.
- تحقق عن طريق الضرب.
عندما يكون الحد المتوسط سالبًا ويكون المصطلح الأخير إيجابيًا، يجب أن تكون العلامات في الحدين سالبة.
عامل بالكامل:\(6 b^{2}-13 b+5\)
- إجابة
-
ضع في اعتبارك جميع مجموعات العوامل.تم ترتيب الثلاثي بالفعل ترتيبًا تنازليًا. 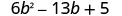
ابحث عن عوامل الفصل الدراسي الأول. 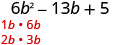
ابحث عن عوامل الفصل الأخير. ضع في اعتبارك العلامات. منذ الفصل الأخير، يعتبر 5 إيجابيًا، ويجب أن تكون العوامل إيجابية أو كلاهما سلبية. معامل المدى المتوسط سلبي، لذلك نستخدم العوامل السلبية. 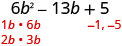
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 b-1)(3 b-5)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 v}\checkmark \end{array}\end{array}\)\(6 b^{2}-13 b+5\) العوامل المحتملة المنتج \ (6 b^ {2} -13 b+5\) العوامل المحتملة» data-valign= «top» class="lt-math-15168"> (b−1) (6b−5) \ (6 b^ {2} -13 b+5\) المنتج» data-valign= «top» class="lt-math-15168">\(6 b^{2}-11 b+5\) \ (6 b^ {2} -13 b+5\) العوامل المحتملة» data-valign= «top» class="lt-math-15168"> (b−5) (6b−1) \ (6 b^ {2} -13 b+5\) المنتج» data-valign= «top» class="lt-math-15168">\(6 b^{2}-31 b+5\) \ (6 b^ {2} -13 b+5\) العوامل المحتملة» data-valign= «top» class="lt-math-15168"> (2b−1) (3b−5) \ (6 b^ {2} -13 b+5\) المنتج» data-valign= «top» class="lt-math-15168">\(6 b^{2}-13 b+5\) * \ (6 b^ {2} -13 b+5\) العوامل المحتملة» data-valign= «top» class="lt-math-15168"> (2b−5) (3b−1) \ (6 b^ {2} -13 b+5\) المنتج» data-valign= «top» class="lt-math-15168">\(6 b^{2}-17 b+5\)
عامل بالكامل:\(8 x^{2}-14 x+3\)
- إجابة
-
\((2 x-3)(4 x-1)\)
عامل بالكامل:\(10 y^{2}-37 y+7\)
- إجابة
-
\((2 y-7)(5 y-1)\)
عندما نضع تعبيرًا في الاعتبار، فإننا نبحث دائمًا عن العامل المشترك الأكبر أولاً. إذا لم يكن للتعبير عامل مشترك أكبر، فلا يمكن أن يكون هناك عامل واحد في عوامله أيضًا. قد يساعدنا هذا في التخلص من بعض تركيبات العوامل المحتملة.
عامل بالكامل:\(14 x^{2}-47 x-7\)
- إجابة
-
ضع في اعتبارك جميع مجموعات العوامل. نستخدم كل زوج من عوامل العدد 14\(x^{2}\) مع كل زوج من العوامل التي تساوي −7.تم ترتيب الثلاثي بالفعل ترتيبًا تنازليًا. 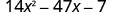
ابحث عن عوامل الفصل الدراسي الأول. 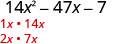
ابحث عن عوامل الفصل الأخير. ضع في اعتبارك العلامات. نظرًا لأنه سلبي، يجب أن يكون أحد العوامل إيجابيًا والآخر سلبيًا. 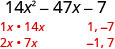
عوامل\(14x^2\) اقترن مع عوامل −7 \ (14x^2\)» data-valign= «top» class="lt-math-15168">\(x, 14 x\) 11، −7
−7، 11
(ترتيب عكسي)\ (14x^2\)» data-valign= «top» class="lt-math-15168">\(x, 14 x\) −1، 77
77، −1
(ترتيب عكسي)\ (14x^2\)» data-valign= «top» class="lt-math-15168">\(2x,7x\) 11، −7
−7، 11
(ترتيب عكسي)\ (14x^2\)» data-valign= «top» class="lt-math-15168">\(2x,7x\) −1، 77
77، −1
(ترتيب عكسي)تؤدي هذه الأزواج إلى المجموعات الثمانية التالية.
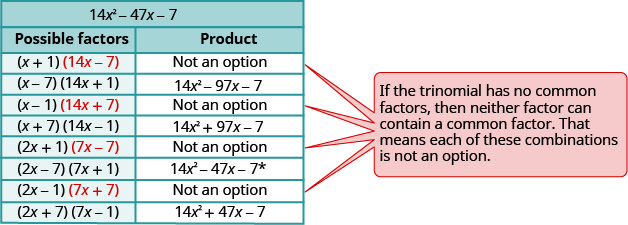
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 x-7)(7 x+1)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 }\checkmark \end{array}\end{array}\)
عامل بالكامل:\(8 a^{2}-3 a-5\)
- إجابة
-
\((a-1)(8 a+5)\)
عامل بالكامل:\(6 b^{2}-b-15\)
- إجابة
-
\((2 b+3)(3 b-5)\)
عامل بالكامل:\(18 n^{2}-37 n+15\)
- إجابة
-
تم ترتيب الثلاثي بالفعل ترتيبًا تنازليًا. \(18 n^{2}-37 n+15\) ابحث عن عوامل الفصل الدراسي الأول. 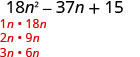
ابحث عن عوامل الفصل الأخير. ضع في اعتبارك العلامات. نظرًا لأن 15 إيجابي ومعامل المدى المتوسط سلبي، فإننا نستخدم العوامل السلبية. 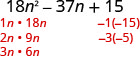
ضع في اعتبارك جميع مجموعات العوامل.

\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 n-3)(9 n-5)\\\\\text {Check by multiplying. } \\\\ \begin{array}{l}{(2 n-3)(9 n-5)} \\ {18 n^{2}-10 n-27 n+15} \\ {18 n^{2}-37 n+15 } \checkmark\end{array} \end{array}\)
عامل بالكامل:\(18 x^{2}-3 x-10\)
- إجابة
-
\((3 x+2)(6 x-5)\)
عامل بالكامل:\(30 y^{2}-53 y-21\)
- إجابة
-
\((3 y+1)(10 y-21)\)
لا تنس البحث عن GCF أولاً.
عامل بالكامل:\(10 y^{4}+55 y^{3}+60 y^{2}\)
- إجابة
-
\(10 y^{4}+55 y^{3}+60 y^{2}\) لاحظ العامل المشترك الأكبر، واضعه في الاعتبار أولاً. 5\(y^{2}\left(2 y^{2}+11 y+12\right)\) عامل ثلاثي الحدود. 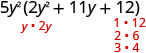
ضع في اعتبارك جميع المجموعات.
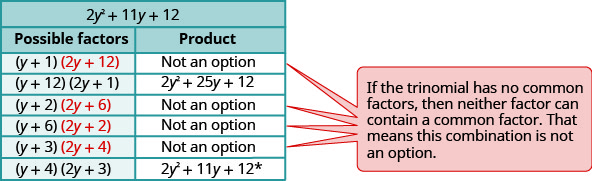
\(\begin{array}{ll}\text{The correct factors are those whose product} &5 y^{2}(y+4)(2 y+3) \\ \text{is the original trinomial. Remember to include} & \\\text {the factor } 5 y^{2}\\\text {Check by multiplying. } \\\\ \begin{array}{l}{5 y^{2}(y+4)(2 y+3)} \\ {5 y^{2}\left(2 y^{2}+8 y+3 y+12\right)} \\ {10 y^{4}+55 y^{3}+60 y^{2}}\checkmark\end{array} \end{array}\)
عامل بالكامل:\(15 n^{3}-85 n^{2}+100 n\)
- إجابة
-
5\(n(n-4)(3 n-5)\)
عامل بالكامل:\(56 q^{3}+320 q^{2}-96 q\)
- إجابة
-
8\(q(q+6)(7 q-2)\)
عوامل ثلاثية الحدود باستخدام طريقة «ac»
هناك طريقة أخرى لحساب القيم الثلاثية للنموذج\(ax^2+bx+c\) وهي طريقة «ac». (يُطلق على طريقة «ac» أحيانًا طريقة التجميع.) تعد طريقة «ac» في الواقع امتدادًا للطرق التي استخدمتها في القسم الأخير لحساب التثليث بالمعامل الرئيسي الأول. هذه الطريقة منظمة للغاية (خطوة بخطوة)، وهي تعمل دائمًا!
عامل:\(6 x^{2}+7 x+2\)
- إجابة
-


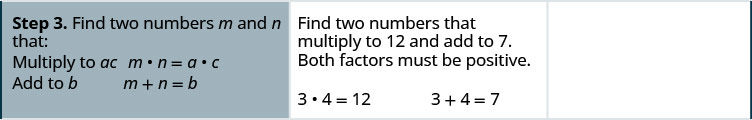



عامل:\(6 x^{2}+13 x+2\)
- إجابة
-
\((x+2)(6 x+1)\)
عامل:\(4 y^{2}+8 y+3\)
- إجابة
-
\((2 y+1)(2 y+3)\)
- عامل أي GCF.
- ابحث عن المنتج ac.
- ابحث عن رقمين m وفي ذلك:
\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\) - قسّم المدى المتوسط باستخدام m و n:
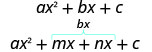
- عامل حسب التجميع.
- تحقق من ذلك بضرب العوامل.
عندما يكون المصطلح الثالث من الثلاثية سالبًا، فإن عوامل المصطلح الثالث ستكون لها علامات معاكسة.
عامل:\(8 u^{2}-17 u-21\)
- إجابة
-
هل هناك عامل مشترك أكبر؟ لا. 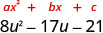
ابحث\(a\cdot c\) \(a\cdot c\) 8 (−21) −168 ابحث عن عددين يضربان في −168 ويضيفان إلى −17. يجب أن يكون العامل الأكبر سلبيًا.
عوامل −168 مجموع العوامل 1، −168 1+ (−168) =−167 2، −84 2+ (−84) = −82 3، −56 3+ (−56) =−53 4، −42 4+ (−42) =−38 6، −28 6+ (−28) =−22 7، −24 7+ (−24) =−17* 8، −21 8+ (−21) =−13 \(\begin{array}{lc}\text { Split the middle term using } 7 u \text { and }-24 u &8 u^{2}-17 u-21 \\ & \qquad\space \swarrow\searrow \\ & \underbrace{8 u^{2}+7 u} \underbrace{-24 u-21} \\ \text { Factor by grouping. } & u(8 u+7)-3(8 u+7) \\ & (8 u+7)(u-3) \\ \text { Check by multiplying. } & \begin{array}{l}{(8 u+7)(u-3)} \\ {8 u^{2}-24 u+7 u-21} \\ {8 u^{2}-17 u-21} \checkmark \end{array} \end{array}\)
عامل:\(20 h^{2}+13 h-15\)
- إجابة
-
\((4 h-5)(5 h+3)\)
عامل:\(6 g^{2}+19 g-20\)
- إجابة
-
\((q+4)(6 q-5)\)
عامل:\(2 x^{2}+6 x+5\)
- إجابة
-
هل هناك عامل مشترك أكبر؟ لا. 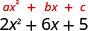
ابحث عن ac ac 2 (5) 10 ابحث عن رقمين يضربان في 10 ويضيفان إلى 6.
العوامل المكونة من 10 مجموع العوامل 1,10 1+10=11 2، 5 2+5 = 7 لا توجد عوامل تتضاعف إلى 10 وتضيف إلى 6. وكثرة الحدود هي الأولية.
عامل:\(10 t^{2}+19 t-15\)
- إجابة
-
\((2 t+5)(5 t-3)\)
عامل:\(3 u^{2}+8 u+5\)
- إجابة
-
\((u+1)(3 u+5)\)
لا تنس البحث عن عامل مشترك!
عامل:\(10 y^{2}-55 y+70\)
- إجابة
-
هل هناك عامل مشترك أكبر؟ نعم. GCF هو 5. 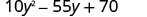
ضع في اعتبارك ذلك. احرص على الحفاظ على عامل 5 طوال الحل! 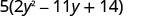
يحتوي الثلاثي الموجود داخل الأقواس على معامل رئيسي ليس 1. 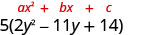
عامل ثلاثي الحدود. 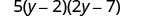
تحقق من ذلك بضرب جميع العوامل الثلاثة. 5\(\left(2 y^{2}-2 y-4 y+14\right)\) 5\(\left(2 y^{2}-11 y+14\right)\) \(10 y^{2}-55 y+70\)✓
عامل:\(16 x^{2}-32 x+12\)
- إجابة
-
4\((2 x-3)(2 x-1)\)
عامل:\(18 w^{2}-39 w+18\)
- إجابة
-
3\((3 w-2)(2 w-3)\)
يمكننا الآن تحديث إستراتيجية التخصيم الأولية، كما هو موضح في الشكل\(\PageIndex{1}\) ومفصّل في اختيار إستراتيجية لحساب كثيرات الحدود بالكامل (محدثة)، لتضمين القيم الثلاثية للنموذج\(a x^{2}+b x+c\). تذكر أن بعض كثيرات الحدود أولية وبالتالي لا يمكن أخذها في الاعتبار.

- هل هناك عامل مشترك أكبر؟
- ضع في اعتبارك ذلك.
- هل كثير الحدود عبارة عن معادلة ذات حدين أو ثلاثية أو أكثر من ثلاثة حدود؟
- إذا كانت ذات حدين، فليس لدينا الآن طريقة لأخذها في الاعتبار.
- إذا كانت عبارة عن ثلاثية من النموذج Undo\(x^{2}+b x+c\)
FOIL\\((x\qquad)(x\qquad)\). - إذا كانت عبارة عن ثلاثة حدود للنموذج،\(a x^{2}+b x+c\)
استخدم التجربة والخطأ أو طريقة «ac». - إذا كان يحتوي على أكثر من ثلاثة مصطلحات
استخدم طريقة التجميع.
- تحقق من ذلك بضرب العوامل.
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع احتساب القيم الثلاثية للنموذج\(a x^{2}+b x+c\)
المفاهيم الرئيسية
- العوامل الثلاثية للنموذج\(a x^{2}+b x+c\) باستخدام التجربة والخطأ: انظر المثال.
- اكتب ثلاثية الحدود بترتيب تنازلي للدرجات.
- ابحث عن جميع أزواج عوامل الحد الأول.
- ابحث عن جميع أزواج عوامل الحد الثالث.
- اختبر جميع المجموعات الممكنة من العوامل حتى يتم العثور على المنتج الصحيح.
- تحقق عن طريق الضرب.
- معاملات ثلاثية الحدود للنموذج\(a x^{2}+b x+c\) باستخدام طريقة «ac»: انظر المثال.
- عامل أي GCF.
- ابحث عن المنتج ac.
- ابحث عن رقمين m وفي ذلك:\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
- قسّم المدى المتوسط باستخدام m و n:
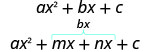
- عامل حسب التجميع.
- تحقق من ذلك بضرب العوامل.
- اختر إستراتيجية لحساب كثيرات الحدود بالكامل (محدثة):
- هل هناك عامل مشترك أكبر؟ ضع في اعتبارك ذلك.
- هل كثير الحدود عبارة عن معادلة ذات حدين أو ثلاثية أو أكثر من ثلاثة حدود؟
إذا كانت ذات حدين، فليس لدينا الآن طريقة لأخذها في الاعتبار.
إذا كانت عبارة عن ثلاثية من النموذج Undo\(x^2+bx+c\)
FOIL\((x\qquad)(x\qquad)\).
إذا كانت عبارة عن ثلاثة حدود للنموذج،\(ax^2+bx+c\)
استخدم التجربة والخطأ أو طريقة «ac».
إذا كان يحتوي على أكثر من ثلاثة مصطلحات
استخدم طريقة التجميع. - تحقق من ذلك بضرب العوامل.
مسرد المصطلحات
- كثيرات الحدود الأولية
- وكثيرات الحدود التي لا يمكن أخذها في الاعتبار هي كثيرات الحدود الأولية.


