6.4: منتجات خاصة
- Page ID
- 200537
في نهاية هذا القسم، ستكون قادرًا على:
- ضع مربعًا ذو حدين باستخدام نمط المربعات ذات الحدين
- ضرب الاقترانات باستخدام حاصل ضرب نمط المترافقين
- التعرف على نمط المنتج الخاص المناسب واستخدامه
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
تبسيط: أ.\(9^2\) ب.\((−9)^2\) ج\(−9^2\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.5.13.
مربع معادلة ذات حدين باستخدام نمط المربعات ذات الحدين
يحب علماء الرياضيات البحث عن الأنماط التي ستجعل عملهم أسهل. وخير مثال على ذلك هو تربيع المعادلات ذات الحدين. بينما يمكنك دائمًا الحصول على المنتج عن طريق كتابة المعادلة ذات الحدين مرتين واستخدام أساليب القسم الأخير، إلا أنه لا يوجد الكثير من العمل الذي يتعين عليك القيام به إذا تعلمت استخدام النمط.
\[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]
انظر إلى هذه النتائج. هل ترى أي أنماط؟
ماذا عن عدد المصطلحات؟ في كل مثال، قمنا بتربيع معادلة ذات حدين وكانت النتيجة ثلاثية الحدود.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]
انظر الآن إلى الفصل الأول في كل نتيجة. من أين أتت؟
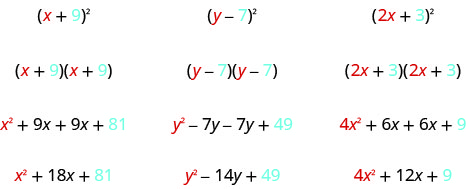
المصطلح الأول هو نتاج المصطلحات الأولى لكل معادلة ذات حدين. نظرًا لأن الحدين متطابقان، فهو مجرد مربع المصطلح الأول!
\[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]
للحصول على الفصل الأول للمنتج، قم بتربيع المصطلح الأول.
من أين جاء الفصل الأخير؟ انظر إلى الأمثلة وابحث عن النمط.
المصطلح الأخير هو نتاج المصطلحات الأخيرة، وهو مربع الفصل الأخير.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]
للحصول على الفصل الأخير من المنتج، قم بتربيع الفصل الأخير.
أخيرًا، انظر إلى المدى المتوسط. لاحظ أنه جاء من إضافة المصطلحين «الخارجي» و «الداخلي» - وكلاهما متشابهان! لذا فإن الحد الأوسط هو ضعف ناتج مصطلحي المعادلة ذات الحدين.
\[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]
\[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]
للحصول على المدى المتوسط للمنتج، اضرب المصطلحات وضاعف منتجها.
وضع كل ذلك معًا:
إذا كانت\(a\) أعدادًا حقيقية، فإن نمط المربع ذي الحدين هو\(b\)
\[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2} + \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]
تطبيق هذا على نوعين من الحدين:
\[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]
لتربيع المعادلة ذات الحدين:
- مربع، الفصل الأول
- مربع الفصل الأخير
- مضاعفة منتجهم
يساعد مثال رقمي في التحقق من النمط.
\(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)
للضرب\((10+4)^2\) عادة ما تتبع ترتيب العمليات.
\[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]
يعمل النمط!
\(\text { Multiply: }(x+5)^{2}\)
الحل:
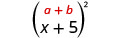 |
|
| مربع الفصل الدراسي الأول. |  |
| مربع الفصل الأخير. |  |
| ضاعف المنتج. |  |
| قم بالتبسيط. | \(x^{2}+10 x+25\) |
اضرب:\((x+9)^{2}\)
- إجابة
-
\(x^{2}+18 x+81\)
اضرب:\((y+11)^{2}\)
- إجابة
-
\(y^{2}+22 y+121\)
اضرب:\((y-3)^{2}\)
الحل:
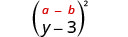 |
|
| مربع الفصل الدراسي الأول. |  |
| مربع الفصل الأخير. |  |
| ضاعف المنتج. | 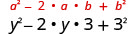 |
| قم بالتبسيط. | \(y^{2}-6 y+9\) |
اضرب:\((x-9)^{2}\)
- إجابة
-
\(x^{2}-18 x+81\)
اضرب:\((p-13)^{2}\)
- إجابة
-
\(p^{2}-26 p+169\)
اضرب:\((4 x+6)^{2}\)
الحل:
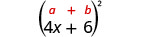 |
|
| استخدم النمط. | 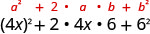 |
| قم بالتبسيط. | \(16 x^{2}+48 x+36\) |
اضرب:\((6 x+3)^{2}\)
- إجابة
-
\(36 x^{2}+36 x+9\)
اضرب:\((4 x+9)^{2}\)
- إجابة
-
\(16 x^{2}+72 x+81\)
اضرب:\((2 x-3 y)^{2}\)
الحل:
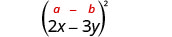 |
|
| استخدم النمط. | 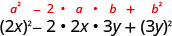 |
| قم بالتبسيط. | \(4 x^{2}-12 x y+9 y^{2}\) |
اضرب:\((2 c-d)^{2}\)
- إجابة
-
\(4 c^{2}-4 c d+d^{2}\)
اضرب:\((4 x-5 y)^{2}\)
- إجابة
-
\(16 x^{2}-40 x y+25 y^{2}\)
اضرب:\(\left(4 u^{3}+1\right)^{2}\)
الحل:
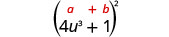 |
|
| استخدم النمط. | 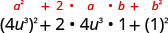 |
| قم بالتبسيط. | \(16 u^{6}+8 u^{3}+1\) |
اضرب:\(\left(2 x^{2}+1\right)^{2}\)
- إجابة
-
\(4 x^{4}+4 x^{2}+1\)
اضرب:\(\left(3 y^{3}+2\right)^{2}\)
- إجابة
-
\(9 y^{6}+12 y^{3}+4\)
ضرب المترادفات باستخدام حاصل ضرب نمط الاقتران
لقد رأينا للتو نمطًا لتربيع المقادير ذات الحدين يمكننا استخدامه لتسهيل ضرب بعض المقادير ذات الحدين. وبالمثل، هناك نمط لمنتج آخر من المعادلات ذات الحدين. ولكن قبل أن نصل إليها، نحتاج إلى تقديم بعض المفردات.
ماذا تلاحظ عن هذه الأزواج من الحدين؟
\[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]
انظر إلى المصطلح الأول لكل معادلة ذات حدين في كل زوج.
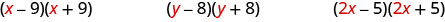
لاحظ أن المصطلحات الأولى هي نفسها في كل زوج.
انظر إلى المصطلحات الأخيرة لكل معادلة ذات حدين في كل زوج.
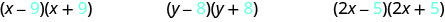
لاحظ أن المصطلحات الأخيرة هي نفسها في كل زوج.
لاحظ كيف أن كل زوج له مبلغ واحد وفرق واحد.
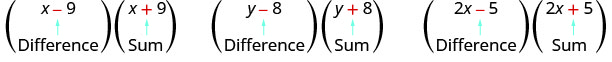
زوج من الحدين لكل منهما نفس المصطلح الأول ونفس المصطلح الأخير، ولكن الواحد هو المجموع والآخر هو الفرق له اسم خاص. ويسمى الزوج المترافق وهو على شكل (a−b)، (a+b).
الزوج المترافق عبارة عن وحدين من الشكل
\[(a-b),(a+b)\nonumber \]
لكل زوج من الحدين نفس الحد الأول ونفس الحد الأخير، ولكن أحد الحدين هو المجموع والآخر هو الفرق.
هناك نمط جميل للعثور على منتج المترادفات. يمكنك بالطبع ببساطة الحصول على المنتج، ولكن استخدام النمط يجعل عملك أسهل.
دعونا نبحث عن النمط باستخدام FOIL لمضاعفة بعض الأزواج المترافقة.
\[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]
كل مصطلح أول هو نتاج المصطلحات الأولى من الحدين، وبما أنها متطابقة فهو مربع المصطلح الأول.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]
المصطلح الأخير جاء من ضرب الحدود الأخيرة، مربع الحد الأخير.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]
ماذا تلاحظ عن المنتجات؟
منتج الحدين هو أيضًا معادلة ذات حدين! معظم المنتجات الناتجة عن FOIL كانت ثلاثية الأبعاد.
لماذا لا يوجد مصطلح متوسط؟ لاحظ أن الحدين المتوسطين اللذين تحصل عليهما من FOIL يتحدان إلى 0 في كل حالة، نتيجة الجمع الواحدة والطرح الواحد.
يكون منتج الاقتران دائمًا بالشكل\(a^2-b^2\). وهذا ما يسمى بفرق المربعات.
هذا يؤدي إلى النمط:
إذا كانت\(a\)\(b\) الأرقام حقيقية،

يُطلق على المنتج اسم اختلاف المربعات.
لضرب المترافقات، قم بمربع الحد الأول، ومربع الحد الأخير، واكتب حاصل الضرب في صورة فرق بين المربعات.
لنختبر هذا النمط بمثال رقمي.
\(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)
لاحظ أن النتيجة هي نفسها!
اضرب:\((x-8)(x+8)\)
الحل:
أولاً، تعرف على هذا كمنتج للمقترنات. تحتوي المقادير ذات الحدين على نفس الشروط الأولى، ونفس الشروط الأخيرة، وأحد الحدين عبارة عن مجموع والآخر فرق.
| يناسب النمط. | 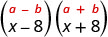 |
| مربع الفصل الأول، x. | 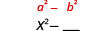 |
| مربع الفصل الأخير، 8. | 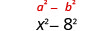 |
| المنتج هو اختلاف المربعات. | 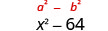 |
اضرب:\((x-5)(x+5)\)
- إجابة
-
\(x^{2}-25\)
اضرب:\((w-3)(w+3)\)
- إجابة
-
\(w^{2}-9\)
اضرب:\((2 x+5)(2 x-5)\)
الحل:
هل يترافق الحدان؟
| إنه نتاج الاقتران. | 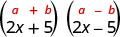 |
| مربع الفصل الأول، 2 x. | 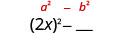 |
| مربع الفصل الأخير، 5. | 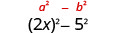 |
| قم بالتبسيط. المنتج هو اختلاف المربعات. | 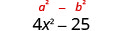 |
اضرب:\((6 x+5)(6 x-5)\)
- إجابة
-
\(36 x^{2}-25\)
اضرب:\((2 x+7)(2 x-7)\)
- إجابة
-
\(4 x^{2}-49\)
قد تنظر المعادلات ذات الحدين في المثال التالي إلى الوراء - المتغير موجود في الفصل الثاني. لكن كلا الحدين لا يزالان مترافقين، لذلك نستخدم نفس النمط لضربهما.
ابحث عن المنتج:\((3+5 x)(3-5 x)\)
الحل:
| إنه نتاج الاقتران. | 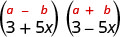 |
| استخدم النمط. | 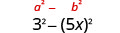 |
| قم بالتبسيط. | \(9-25 x^{2}\) |
اضرب:\((7+4 x)(7-4 x)\)
- إجابة
-
\(49-16 x^{2}\)
اضرب:\((9-2 y)(9+2 y)\)
- إجابة
-
\(81-4 y^{2}\)
الآن سنضرب المترابطات التي تحتوي على متغيرين.
ابحث عن المنتج:\((5 m-9 n)(5 m+9 n)\)
الحل:
| هذا يناسب النمط. | 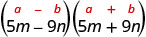 |
| استخدم النمط. | 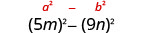 |
| قم بالتبسيط. | \(25 m^{2}-81 n^{2}\) |
ابحث عن المنتج:\((4 p-7 q)(4 p+7 q)\)
- إجابة
-
\(16 p^{2}-49 q^{2}\)
ابحث عن المنتج:\((3 x-y)(3 x+y)\)
- إجابة
-
\(9 x^{2}-y^{2}\)
ابحث عن المنتج:\((c d-8)(c d+8)\)
الحل:
| هذا يناسب النمط. | 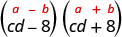 |
| استخدم النمط. | 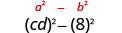 |
| قم بالتبسيط. | \(c^{2} d^{2}-64\) |
ابحث عن المنتج:\((x y-6)(x y+6)\)
- إجابة
-
\(x^{2} y^{2}-36\)
ابحث عن المنتج:\((a b-9)(a b+9)\)
- إجابة
-
\(a^{2} b^{2}-81\)
ابحث عن المنتج:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)
الحل:
| هذا يناسب النمط. | 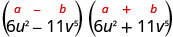 |
| استخدم النمط. | 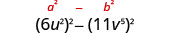 |
| قم بالتبسيط. | \(36 u^{4}-121 v^{10}\) |
ابحث عن المنتج:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)
- إجابة
-
\(9 x^{4}-16 y^{6}\)
ابحث عن المنتج:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)
- إجابة
-
\(4 m^{4}-25 n^{6}\)
التعرف على نمط المنتج الخاص المناسب واستخدامه
لقد قمنا للتو بتطوير أنماط منتجات خاصة للمربعات ذات الحدين ولمنتج المترافقات. تبدو المنتجات متشابهة، لذلك من المهم التعرف على الوقت المناسب لاستخدام كل من هذه الأنماط وملاحظة مدى اختلافها. انظر إلى النموذجين معًا ولاحظ أوجه التشابه والاختلاف بينهما.
\(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)
اختر النمط المناسب واستخدمه للعثور على المنتج:
- \((2 x-3)(2 x+3)\)
- \((8 x-5)^{2}\)
- \((6 m+7)^{2}\)
- \((5 x-6)(6 x+5)\)
الحل:
1. \((2x−3)(2x+3)\)هذه هي المرادفات. لديهم نفس الأرقام الأولى، ونفس الأرقام الأخيرة، وأحد الحدين هو المجموع والآخر هو الفرق. يناسب نمط المنتج المترافق.
| هذا يناسب النمط. | 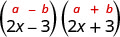 |
| استخدم النمط. | 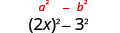 |
| قم بالتبسيط. | \(4 x^{2}-9\) |
2. \((8 x-5)^{2}\)يُطلب منا وضع معادلة ذات حدين. يناسب نمط المربعات ذات الحدين.
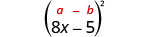 |
|
| استخدم النمط. |  |
| قم بالتبسيط. | \(64 x^{2}-80 x+25\) |
3. \((6 m+7)^{2}\)مرة أخرى، سنقوم بتربيع معادلة ذات حدين حتى نستخدم نمط المربعات ذات الحدين.
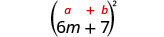 |
|
| استخدم النمط. |  |
| قم بالتبسيط. | \(36 m^{2}+84 m+49\) |
4. \((5 x-6)(6 x+5)\)هذا المنتج لا يناسب الأنماط، لذلك سنستخدم FOIL.
\(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)
اختر النمط المناسب واستخدمه للعثور على المنتج:
- \((9b−2)(2b+9)\)
- \((9p−4)2\)
- \((7y+1)^2\)
- \((4r-3)(4r+3)\)
- إجابة
-
- رقائق؛\(18 b^{2}+77 b-18\)
- مربعات ذات حدين؛\(81 p^{2}-72 p+16\)
- مربعات ذات حدين؛\(49 y^{2}+14 y+1\)
- منتج من المترادفات؛\(16 r^{2}-9\)
اختر النمط المناسب واستخدمه للعثور على المنتج:
- \((6x+7)^2\)
- \((3x−4)(3x+4)\)
- \((2x−5)(5x−2)\)
- \((6n−1)^2\)
- إجابة
-
- مربعات ذات حدين؛\(36 x^{2}+84 x+49\)
- منتج من المترادفات؛\(9 x^{2}-16\)
- رقائق؛\(10 x^{2}-29 x+10\)
- مربعات ذات حدين؛\(36 n^{2}-12 n+1\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع المنتجات الخاصة:
- منتجات خاصة
المفاهيم الرئيسية
- نمط المربعات ذات الحدين
- إذا كانت أ، ب هي أرقام حقيقية،
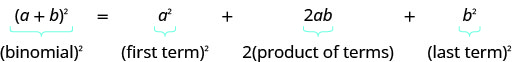
- \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
- \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
- لتربيع الحد ذي الحدين: مربع الحد الأول، مربع المصطلح الأخير، ضعف الناتج.
- إذا كانت أ، ب هي أرقام حقيقية،
- منتج من نمط المترادفات
- إذا كانت أ، ب، ب هي أرقام حقيقية،
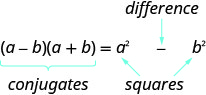
- \((a-b)(a+b)=a^{2}-b^{2}\)
- يُطلق على المنتج اسم اختلاف المربعات.
- إذا كانت أ، ب، ب هي أرقام حقيقية،
- لمضاعفة المترابطات:
- مربع، مربع الحد الأول، المربع، الحد الأخير، اكتبه في صورة فرق بين المربعات
مسرد المصطلحات
- زوج مترافق
- الزوج المترافق عبارة عن وحدتين في الشكل\((a+b)\)؛\((a−b)\) ولكل زوج من الحدين نفس الحد الأول ونفس الحد الأخير، لكن أحد الحدين هو المجموع والآخر فرق.


