6.3E: تمارين
- Page ID
- 200518
الممارسة تجعل من الكمال
ضرب كثير الحدود في معادلة أحادية الحد
في التمارين التالية، اضرب.
4\((w+10)\)
- إجابة
-
4 وات+40
6 (ب+8)
−3 (+7)
- إجابة
-
−3a−21
−5 (ص+9)
2 (x−7)
- إجابة
-
2x−14
7 (ص-4)
−3 (k−4)
- إجابة
-
−3k+12
−8 (j−5)
أ (ث+5)
- إجابة
-
\(q^{2}+5 q\)
(كيلومتر+7)
−ب (ب+9)
- إجابة
-
\(-b^{2}-9 b\)
−ص (ص+3)
−س (x−10)
- إجابة
-
\(-x^{2}+10 x\)
−p (ص−15)
6 (4+ثانية)
- إجابة
-
\(24 r^{2}+6 r s\)
5 درجة مئوية (9 ج+د)
12x (x−10)
- إجابة
-
\(12 x^{2}-120 x\)
9 م (م - 11)
−9 أ (3أ+5)
- إجابة
-
\(-27 a^{2}-45 a\)
−4 بكسل (2p+7)
3\(\left(p^{2}+10 p+25\right)\)
- إجابة
-
\(3 p^{2}+30 p+75\)
6\(\left(y^{2}+8 y+16\right)\)
\(-8 x\left(x^{2}+2 x-15\right)\)
- إجابة
-
\(-8 x^{3}-16 x^{2}+120 x\)
\(-5 t\left(t^{2}+3 t-18\right)\)
5\(q^{3}\left(q^{3}-2 q+6\right)\)
- إجابة
-
\(5 q^{6}-10 q^{4}+30 q^{3}\)
4\(x^{3}\left(x^{4}-3 x+7\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- إجابة
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- إجابة
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- إجابة
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 m-9) m\)
- إجابة
-
\(2 m^{2}-9 m\)
\((8 j-1) j\)
\((w-6) \cdot 8\)
- إجابة
-
\(8 w-48\)
\((k-4) \cdot 5\)
4\((x+10)\)
- إجابة
-
4 × 40
6 (+8)
15 (ص-24)
- إجابة
-
15r−360
12 (ضد -30)
−3 (م+11)
- إجابة
-
−3 م −33
−4 (ص+15)
−8 (z−5)
- إجابة
-
−8z+40
−3 (x−9)
(حتى +5)
- إجابة
-
\(u^{2}+5 u\)
\(q(q+7)\)
\(n\left(n^{2}-3 n\right)\)
- إجابة
-
\(n^{3}-3 n^{2}\)
\(s\left(s^{2}-6 s\right)\)
6\(x(4 x+y)\)
- إجابة
-
\(24 x^{2}+6 x y\)
5 أ (9 أ+ب)
5 ص (11p−5q)
- إجابة
-
\(55 p^{2}-25 p q\)
12\(u(3 u-4 v)\)
3\(\left(v^{2}+10 v+25\right)\)
- إجابة
-
\(3 v^{2}+30 v+75\)
6\(\left(x^{2}+8 x+16\right)\)
2\(n\left(4 n^{2}-4 n+1\right)\)
- إجابة
-
\(8 n^{3}-8 n^{2}+2 n\)
3\(r\left(2 r^{2}-6 r+2\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- إجابة
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- إجابة
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- إجابة
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 y-9) y\)
- إجابة
-
\(18 y^{2}-9 y\)
\((8 b-1) b\)
ضرب معادلة ذات حدين في معادلة ذات حدين
في التمارين التالية، اضرب المقادير ذات الحدين التالية باستخدام: ⓐ خاصية التوزيع ⓑ طريقة FOIL ⓒ الطريقة الرأسية.
(ث+5) (ث+7)
- إجابة
-
\(w^{2}+12 w+35\)
(y+9) (y+3)
(ص+11) (ص-4)
- إجابة
-
\(p^{2}+7 p-44\)
(ث+4) (q−8)
في التمارين التالية، اضرب الحدين. استخدم أي طريقة.
(x+8) (x+3)
- إجابة
-
\(x^{2}+11 x+24\)
(+7) (+4)
(ص-6) (y−2)
- إجابة
-
\(y^{2}-8 y+12\)
(x−7) (x−2)
(ث-4) (ث+7)
- إجابة
-
\(w^{2}+3 w-28\)
\((q-5)(q+8)\)
(ص+12) (ص -5)
- إجابة
-
\(p^{2}+7 p-60\)
(م +11) (م -4)
(6 ص+5) (ص+1)
- إجابة
-
\(6 p^{2}+11 p+5\)
\((7 m+1)(m+3)\)
(2t−9) (10t+1)
- إجابة
-
\(20 t^{2}-88 t-9\)
(3−8) (11r+1)
(5x−y) (3x−6)
- إجابة
-
\(15 x^{2}-3 x y-30 x+6 y\)
(10a−b) (3a−4)
(أ+ب) (2 أ+3 ب)
- إجابة
-
\(2 a^{2}+5 a b+3 b^{2}\)
(ص+ثانية) (3r+2 ثانية)
(4z−y) (z−6)
- إجابة
-
\(4 z^{2}-24 z-z y+6 y\)
(5x−y) (x−4)
\(\left(x^{2}+3\right)(x+2)\)
- إجابة
-
\(x^{3}+2 x^{2}+3 x+6\)
\(\left(y^{2}-4\right)(y+3)\)
\(\left(x^{2}+8\right)\left(x^{2}-5\right)\)
- إجابة
-
\(x^{4}+3 x^{2}-40\)
\(\left(y^{2}-7\right)\left(y^{2}-4\right)\)
(5ab−1) (2ab+3)
- إجابة
-
\(10 a^{2} b^{2}+13 a b-3\)
(2xy+3) (3xy+2)
(6pq−3) (4pq−5)
- إجابة
-
\(24 p^{2} q^{2}-42 p q+15\)
(3s-7) (3rs−4)
ضرب ثلاثية الحدود في معادلة ذات حدين
في التمارين التالية، اضرب باستخدام ⓐ خاصية التوزيع ⓑ الطريقة الرأسية.
\((x+5)\left(x^{2}+4 x+3\right)\)
- إجابة
-
\(x^{3}+9 x^{2}+23 x+15\)
\((u+4)\left(u^{2}+3 u+2\right)\)
\((y+8)\left(4 y^{2}+y-7\right)\)
- إجابة
-
\(4 y^{3}+33 y^{2}+y-56\)
\((a+10)\left(3 a^{2}+a-5\right)\)
في التمارين التالية، اضرب. استخدم أي من الطريقتين.
\((w-7)\left(w^{2}-9 w+10\right)\)
- إجابة
-
\(w^{3}-16 w^{2}+73 w-70\)
\((p-4)\left(p^{2}-6 p+9\right)\)
\((3 q+1)\left(q^{2}-4 q-5\right)\)
- إجابة
-
\(3 q^{3}-11 q^{2}-19 q-5\)
\((6 r+1)\left(r^{2}-7 r-9\right)\)
ممارسة مختلطة
(10−6) + (4−7)
- إجابة
-
14-13
(15p−4) + (3p−5)
\(\left(x^{2}-4 x-34\right)-\left(x^{2}+7 x-6\right)\)
- إجابة
-
−11×−28
\(\left(j^{2}-8 j-27\right)-\left(j^{2}+2 j-12\right)\)
5\(q\left(3 q^{2}-6 q+11\right)\)
- إجابة
-
\(15 q^{3}-30 q^{2}+55 q\)
8\(t\left(2 t^{2}-5 t+6\right)\)
(s −7) (+9)
- إجابة
-
\(s^{2}+2 s-63\)
(x−5) (x+13)
\(\left(y^{2}-2 y\right)(y+1)\)
- إجابة
-
\(y^{3}-y^{2}-2 y\)
\(\left(a^{2}-3 a\right)(4 a+5)\)
\((3 n-4)\left(n^{2}+n-7\right)\)
- إجابة
-
\(3 n^{3}-n^{2}-25 n+28\)
\((6 k-1)\left(k^{2}+2 k-4\right)\)
\((7 p+10)(7 p-10)\)
- إجابة
-
\(49 p^{2}-100\)
(3y+8) (3y−8)
\(\left(4 m^{2}-3 m-7\right) m^{2}\)
- إجابة
-
\(4 m^{4}-3 m^{3}-7 m^{2}\)
\(\left(15 c^{2}-4 c+5\right) c^{4}\)
\((5 a+7 b)(5 a+7 b)\)
- إجابة
-
\(25 a^{2}+70 a b+49 b^{2}\)
(3x−11y) (3x−11y)
(4+12z) (4y−12z)
- إجابة
-
\(16 y^{2}-144 z^{2}\)
الرياضيات اليومية
الرياضيات الذهنية يمكنك استخدام الضرب ذو الحدين لضرب الأرقام بدون آلة حاسبة. لنفترض أنك بحاجة إلى الضرب 13 في 15. فكر في 13 كـ 10+3 و 15 كـ 10+5.
- اضرب (10+3) (10+5) بطريقة FOIL.
- اضرب 13 · 15 بدون استخدام الآلة الحاسبة.
- ما هي الطريقة الأسهل بالنسبة لك؟ لماذا؟
الرياضيات الذهنية يمكنك استخدام الضرب ذو الحدين لضرب الأرقام بدون آلة حاسبة. لنفترض أنك بحاجة إلى الضرب 18 في 17. فكِّر في العدد ١٨ باعتباره ٢٠−٢ و١٧ على أنه ٢٠−٣.
- اضرب (20-2) (20-3) بطريقة FOIL.
- اضرب 18 · 17 بدون استخدام الآلة الحاسبة.
- ما هي الطريقة الأسهل بالنسبة لك؟ لماذا؟
- إجابة
-
- 306
- 306
- سوف تتنوع الإجابات.
تمارين الكتابة
ما الطريقة التي تفضل استخدامها عند ضرب نقطتين: خاصية التوزيع، طريقة FOIL، أو الطريقة الرأسية؟ لماذا؟
ما الطريقة التي تفضل استخدامها عند ضرب ثلاثية الحدود في معادلة ذات حدين: خاصية التوزيع أم الطريقة الرأسية؟ لماذا؟
- إجابة
-
سوف تتنوع الإجابات.
اضرب ما يلي:
\(\begin{array}{l}{(x+2)(x-2)} \\ {(y+7)(y-7)} \\ {(w+5)(w-5)}\end{array}\)
اشرح النمط الذي تراه في إجاباتك.
اضرب ما يلي:
\(\begin{array}{l}{(m-3)(m+3)} \\ {(n-10)(n+10)} \\ {(p-8)(p+8)}\end{array}\)
اشرح النمط الذي تراه في إجاباتك.
- إجابة
-
قد تختلف الإجابات.
اضرب ما يلي:
\(\begin{array}{l}{(p+3)(p+3)} \\ {(q+6)(q+6)} \\ {(r+1)(r+1)}\end{array}\)
اشرح النمط الذي تراه في إجاباتك.
اضرب ما يلي:
\(\begin{array}{l}{(x-4)(x-4)} \\ {(y-1)(y-1)} \\ {(z-7)(z-7)}\end{array}\)
اشرح النمط الذي تراه في إجاباتك.
- إجابة
-
قد تختلف الإجابات.
فحص ذاتي
أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.
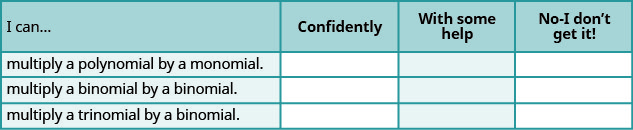
ب- ماذا تخبرك قائمة التحقق هذه عن إتقانك لهذا القسم؟ ما الخطوات التي ستتخذها للتحسين؟


