6.3: ضرب كثيرات الحدود

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• اضرب دالة كثيرة الحدود في معادلة أحادية
• ضرب معادلة ذات حدين في معادلة ذات حدين
• اضرب عددًا ثلاثيًّا في معادلة ذات حدين

ملاحظة

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. توزيع:$2(x+3)$.
   إذا فاتتك هذه المشكلة، راجع التمرين 1.10.31.
2. اجمع بين المصطلحات المتشابهة:$x^{2}+9x+7x+63$.
   إذا فاتتك هذه المشكلة، راجع التمرين 1.3.37.

ضرب كثير الحدود في معادلة أحادية الحد

لقد استخدمنا خاصية التوزيع لتبسيط التعبيرات مثل$2(x−3)$. لقد قمت بضرب كلا المصطلحين بين قوسين$3$،$x$ وبواسطة$2$، للحصول عليهما$2x−6$. باستخدام المفردات الجديدة لهذا الفصل، يمكنك القول أنك قمت بضرب معادلة ذات حدين$x−3$، في حد واحد،$2$.

ضرب المعادلة ذات الحدين في المعادلة الأحادية ليس بالأمر الجديد بالنسبة لك! في ما يلي مثال:

التمارين$\PageIndex{1}$

اضرب:$4(x+3)$.

إجابة

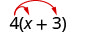
توزيع.	$4 \cdot x+4 \cdot 3$
قم بالتبسيط.	$4 x+12$

التمارين$\PageIndex{2}$

اضرب:$5(x+7)$.

إجابة

5 × +35

التمارين$\PageIndex{3}$

اضرب:$3(y+13)$.

إجابة

3y+39

التمارين$\PageIndex{4}$

الضرب: y (y −2).

إجابة

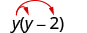
توزيع.	$y \cdot y-y \cdot 2$
قم بالتبسيط.	$y^{2}-2 y$

التمارين$\PageIndex{5}$

اضرب:$x(x−7)$.

إجابة

$x^{2}-7 x$

التمارين$\PageIndex{6}$

اضرب:$d(d−11)$.

إجابة

$d^{2}-11d$

التمارين$\PageIndex{7}$

اضرب:$7x(2 x+y)$

إجابة

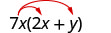
توزيع.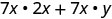
قم بالتبسيط.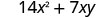

التمارين$\PageIndex{8}$

اضرب:$5x(x+4 y)$

إجابة

$5 x^{2}+20 x y$

التمارين$\PageIndex{9}$

اضرب:$2p(6 p+r)$

إجابة

$12 p^{2}+2 p r$

التمارين$\PageIndex{10}$

اضرب:$-2 y\left(4 y^{2}+3 y-5\right)$

إجابة

توزيع.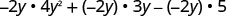
قم بالتبسيط.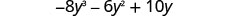

التمارين$\PageIndex{11}$

اضرب:$-3 y\left(5 y^{2}+8 y-7\right)$

إجابة

$-15 y^{3}-24 y^{2}+21 y$

التمارين$\PageIndex{12}$

اضرب:$4x^{2}\left(2 x^{2}-3 x+5\right)$

إجابة

$8 x^{4}-24 x^{3}+20 x^{2}$

التمارين$\PageIndex{13}$

اضرب:$2x^{3}\left(x^{2}-8 x+1\right)$

إجابة

توزيع.	$2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1$
قم بالتبسيط.	$2 x^{5}-16 x^{4}+2 x^{3}$

التمارين$\PageIndex{14}$

الضرب: 4$x\left(3 x^{2}-5 x+3\right)$

إجابة

$12 x^{3}-20 x^{2}+12 x$

التمارين$\PageIndex{15}$

اضرب:$-6 a^{3}\left(3 a^{2}-2 a+6\right)$

إجابة

$-18 a^{5}+12 a^{4}-36 a^{3}$

التمارين$\PageIndex{16}$

اضرب:$(x+3) p$

إجابة

العامل الأحادي هو العامل الثاني.
توزيع.	$x \cdot p+3 \cdot p$
قم بالتبسيط.	\ (\ x p+3 ص)

التمارين$\PageIndex{17}$

اضرب:$(x+8) p$

إجابة

$x p+8 p$

التمارين$\PageIndex{18}$

اضرب:$(a+4) p$

إجابة

$a p+4 p$

ضرب معادلة ذات حدين في معادلة ذات حدين

مثلما توجد طرق مختلفة لتمثيل ضرب الأرقام، هناك العديد من الطرق التي يمكن استخدامها لضرب معادلة ذات حدين في معادلة ذات حدين. سنبدأ باستخدام خاصية التوزيع.

ضرب معادلة ذات حدين في معادلة ذات حدين باستخدام خاصية التوزيع

انظر إلى التمرين$\PageIndex{16}$، حيث قمنا بضرب معادلة ذات حدين في حد واحد.

تعليمات	التعبير
بدء التعبيرات
قمنا بتوزيعها$p$ للحصول على: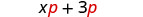
ماذا لو كان لدينا$(x + 7)$ بدلاً من$p$?
قم بالتوزيع$(x + 7)$.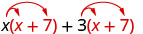
وزّع مرة أخرى.	$x^{2}+7 x+3 x+21$
اجمع بين المصطلحات المتشابهة.	$x^{2}+10 x+21$

لاحظ أنه قبل الجمع بين المصطلحات المتشابهة، كان لديك أربعة فصول. لقد قمت بضرب حدودي أول ذات حدين في الحد الثاني من الحدين - أربعة مضاعفات.

التمارين$\PageIndex{19}$

اضرب:$(y+5)(y+8)$

إجابة

توزيع (ص + 8).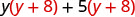
التوزيع مرة أخرى	$y^{2}+8 y+5 y+40$
اجمع بين المصطلحات المتشابهة.	\ (\ y^ {2} +13 y+40)

التمارين$\PageIndex{20}$

اضرب:$(x+8)(x+9)$

إجابة

$x^{2}+17 x+72$

التمارين$\PageIndex{21}$

اضرب:$(5 x+9)(4 x+3)$

إجابة

$20 x^{2}+51 x+27$

التمارين$\PageIndex{22}$

اضرب:$(2 y+5)(3 y+4)$

إجابة

توزيع (3 ص + 4).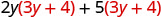
التوزيع مرة أخرى	$6 y^{2}+8 y+15 y+20$
اجمع بين المصطلحات المتشابهة.	$6 y^{2}+23 y+20$

التمارين$\PageIndex{23}$

اضرب:$(3 b+5)(4 b+6)$

إجابة

$12 b^{2}+38 b+30$

التمارين$\PageIndex{24}$

اضرب:$(a+10)(a+7)$

إجابة

$a^{2}+17 a+70$

التمارين$\PageIndex{25}$

اضرب:$(4 y+3)(2 y-5)$

إجابة

قم بالتوزيع.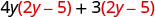
وزّع مرة أخرى.	$8 y^{2}-20 y+6 y-15$
اجمع بين المصطلحات المتشابهة.	$8 y^{2}-14 y-15$

التمارين$\PageIndex{26}$

اضرب:$(5 y+2)(6 y-3)$

إجابة

$30 y^{2}-3 y-6$

التمارين$\PageIndex{27}$

اضرب:$(3 c+4)(5 c-2)$

إجابة

$15 c^{2}+14 c-8$

التمارين$\PageIndex{28}$

اضرب:$(x-2)(x-y)$

إجابة

قم بالتوزيع.
وزّع مرة أخرى.	$x^{2}-x y-2 x+2 y$
لا توجد مصطلحات مماثلة للدمج.

التمارين$\PageIndex{29}$

اضرب:$(a+7)(a-b)$

إجابة

$a^{2}-a b+7 a-7 b$

التمارين$\PageIndex{30}$

اضرب:$(x+5)(x-y)$

إجابة

$x^{2}-x y+5 x-5 y$

ضرب معادلة ذات حدين في معادلة ذات حدين باستخدام طريقة FOIL

تذكر أنه عند ضرب معادلة ذات حدين في معادلة ذات حدين تحصل على أربعة مصطلحات. في بعض الأحيان يمكنك الجمع بين المصطلحات المتشابهة للحصول على ثلاثية الحدود، ولكن في بعض الأحيان، كما هو الحال في التمرين$\PageIndex{28}$، لا توجد مصطلحات مماثلة لدمجها.

دعونا ننظر إلى المثال الأخير مرة أخرى ونولي اهتمامًا خاصًا لكيفية حصولنا على المصطلحات الأربعة.

$$\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y}\end{array} \nonumber$$

من أين جاء الفصل الدراسي الأول؟$x^{2}$

نحن نختصر «الأول، الخارجي، الداخلي، الأخير» باسم FOIL. تشير الأحرف إلى «F أولاً، O Uter، I inner، L ast». من السهل تذكر كلمة FOIL وتضمن العثور على جميع المنتجات الأربعة.

$$\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y} \\ {F \qquad O\qquad I\qquad L}\end{array}$$

دعونا ننظر إلى (x+3) (x+7).

خاصية التوزيع	رقائق
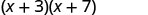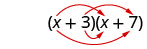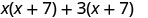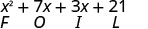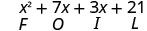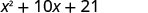	$x^{2}+10 x+21$

لاحظ كيف تتناسب المصطلحات الموجودة في السطر الثالث مع نمط FOIL.

الآن سنقوم بعمل مثال حيث نستخدم نمط FOIL لضرب اثنين من الحدين.

التمارين$\PageIndex{31}$: How to Multiply a Binomial by a Binomial using the FOIL Method

اضرب باستخدام طريقة FOIL:$(x+5)(x+9)$

إجابة

التمارين$\PageIndex{32}$

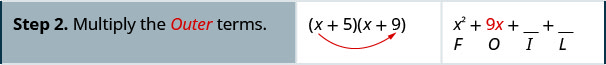
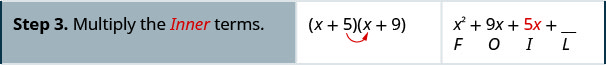
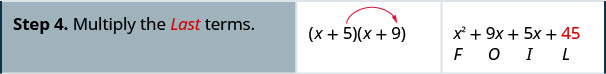
اضرب باستخدام طريقة FOIL:$(x+6)(x+8)$

إجابة

$x^{2}+14 x+48$

التمارين$\PageIndex{33}$

اضرب باستخدام طريقة FOIL:$(y+17)(y+3)$

إجابة

$y^{2}+20 y+51$

نلخص خطوات طريقة FOIL أدناه. تنطبق طريقة FOIL فقط على ضرب المقادير ذات الحدين، وليس على كثيرات الحدود الأخرى!

اضرب نقطتين ذات حدين باستخدام طريقة الفويل

عندما تقوم بالضرب باستخدام طريقة FOIL، فإن رسم الخطوط سيساعد عقلك على التركيز على النمط وتسهيل تطبيقه.

التمارين$\PageIndex{34}$

اضرب:$(y−7)(y+4)$.

إجابة

التمارين$\PageIndex{35}$

اضرب:$(x−7)(x+5)$.

إجابة

$x^{2}-2 x-35$

التمارين$\PageIndex{36}$

اضرب: (b−3) (ب+6).

إجابة

$b^{2}+3 b-18$

التمارين$\PageIndex{37}$

اضرب:$(4x+3)(2x−5)$.

إجابة

التمارين$\PageIndex{38}$

اضرب:$(3x+7)(5x−2)$.

إجابة

$15 x^{2}+29 x-14$

التمارين$\PageIndex{39}$

اضرب:$(4y+5)(4y−10)$.

إجابة

$16 y^{2}-20 y-50$

كانت المنتجات النهائية في الأمثلة الأربعة الأخيرة عبارة عن صيغ ثلاثية الحدود لأننا نستطيع الجمع بين المصطلحين المتوسطين. هذا ليس هو الحال دائمًا.

التمارين$\PageIndex{40}$

اضرب:$(3x−y)(2x−5)$.

إجابة

	$(3 x-y)(2 x-5)$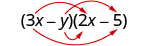
اضرب الأول.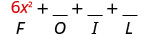
اضرب الرقم الخارجي.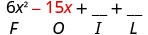
اضرب الرقم الداخلي.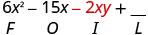
اضرب الأخير.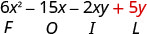
اجمع بين المصطلحات المتشابهة - لا يوجد شيء.	$6 x^{2}-15 x-2 x y+5 y$

التمارين$\PageIndex{41}$

الضرب: (10c−d) (c−6).

إجابة

$10 c^{2}-60 c-c d+6 d$

التمارين$\PageIndex{42}$

اضرب: (7x−y) (2x−5).

إجابة

$14 x^{2}-35 x-2 x y+10 y$

احذر من الأسس في المثال التالي.

التمارين$\PageIndex{43}$

اضرب:$\left(n^{2}+4\right)(n-1)$

إجابة

	$\left(n^{2}+4\right)(n-1)$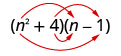
اضرب الأول.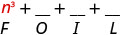
اضرب الرقم الخارجي.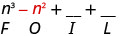
اضرب الرقم الداخلي.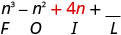
اضرب الأخير.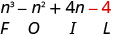
اجمع بين المصطلحات المتشابهة - لا يوجد شيء.	\ (\ n^ {3} -n^ {2} +4 n-4)

التمارين$\PageIndex{44}$

اضرب:$\left(x^{2}+6\right)(x-8)$

إجابة

$x^{3}-8 x^{2}+6 x-48$

التمارين$\PageIndex{45}$

اضرب:$\left(y^{2}+7\right)(y-9)$

إجابة

$y^{3}-9 y^{2}+7 y-63$

التمارين$\PageIndex{46}$

اضرب:$(3 p q+5)(6 p q-11)$

إجابة

	$(3 p q+5)(6 p q-11)$
اضرب الأول.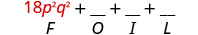
اضرب الرقم الخارجي.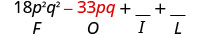
اضرب الرقم الداخلي.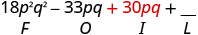
اضرب الأخير.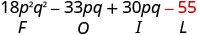
اجمع بين المصطلحات المتشابهة - لا يوجد شيء.	$18 p^{2} q^{2}-3 p q-55$

التمارين$\PageIndex{47}$

اضرب:$(2 a b+5)(4 a b-4)$

إجابة

$8 a^{2} b^{2}+12 a b-20$

التمارين$\PageIndex{48}$

اضرب:$(2 x y+3)(4 x y-5)$

إجابة

$8 x^{2} y^{2}+2 x y-15$

ضرب معادلة ذات حدين في معادلة ذات حدين باستخدام الطريقة الرأسية

عادةً ما تكون طريقة FOIL هي أسرع طريقة لضرب اثنين من الحدين، ولكنها تعمل فقط مع الحدين. يمكنك استخدام خاصية التوزيع للعثور على حاصل ضرب أي من كثيري الحدود. الطريقة الأخرى التي تعمل مع جميع كثيرات الحدود هي الطريقة الرأسية. إنها تشبه إلى حد كبير الطريقة التي تستخدمها لضرب الأرقام الصحيحة. انظر بعناية إلى هذا المثال لضرب الأرقام المكونة من رقمين.

الآن سنقوم بتطبيق نفس الطريقة لضرب اثنين من الحدين.

التمارين$\PageIndex{49}$

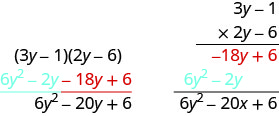
اضرب باستخدام الطريقة الرأسية:$(3 y-1)(2 y-6)$

إجابة

لا يهم أي معادلة ذات حدين توضع في الأعلى.

\[\begin{array}{lll}{\text { Multiply } 3 y-1 \text { by }-6 \text { . }}&& \\ {\text { Multiply } 3 y-1 \text { by } 2 y \text { . }}& &\\ \\ &{\qquad\space3 y-1} & \\& {\dfrac{ \space\space\times 2 y-6}{\quad-18 y+6}} & \text{partial product} & \\ &

ParseError: EOF expected (click for details)

Callstack:
    at (اللغة_العربية/كتاب:_الجبر_الابتدائي_(OpenStax)/06:/6.03:_ضرب_كثيرات_الحدود), /content/body/div[4]/div[3]/div[1]/div/dl/dd/p[2]/span/span, line 1, column 3

& \text{partial product} & \\ \text{Add like terms.} &&\text{product} \end{array}\]

لاحظ أن المنتجات الجزئية هي نفس المصطلحات في طريقة FOIL.

التمارين$\PageIndex{50}$

اضرب باستخدام الطريقة الرأسية:$(5 m-7)(3 m-6)$

إجابة

$15 m^{2}-51 m+42$

التمارين$\PageIndex{51}$

اضرب باستخدام الطريقة الرأسية:$(6 b-5)(7 b-3)$

إجابة

$42 b^{2}-53 b+15$

لقد استخدمنا الآن ثلاث طرق لضرب المقادير ذات الحدين. تأكد من ممارسة كل طريقة، وحاول تحديد الطريقة التي تفضلها. يتم سرد الطرق هنا معًا لمساعدتك على تذكرها.

ضرب اثنين من الحدود

لضرب المقادير ذات الحدين، استخدم:

• خاصية التوزيع
• طريقة فويل
• الطريقة الرأسية

تذكر أن FOIL يعمل فقط عند ضرب اثنين من الحدين.

ضرب ثلاثية الحدود في معادلة ذات حدين

لقد قمنا بضرب وحيدات الحد في وحيدات الحد بكثيرات الحدود وكثيرين الحدين في الحدين. نحن الآن على استعداد لضرب ثلاثية الحدود في معادلة ذات حدين. تذكر أن FOIL لن تعمل في هذه الحالة، ولكن يمكننا استخدام خاصية التوزيع أو الطريقة الرأسية. ننظر أولاً إلى مثال باستخدام خاصية التوزيع.

التمارين$\PageIndex{52}$

اضرب باستخدام خاصية التوزيع:$(b+3)\left(2 b^{2}-5 b+8\right)$

إجابة

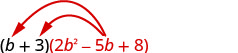
قم بالتوزيع.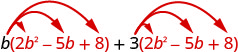
اضرب.	$2 b^{3}-5 b^{2}+8 b+6 b^{2}-15 b+24$
اجمع بين المصطلحات المتشابهة.	$2 b^{3}+b^{2}-7 b+24$

التمارين$\PageIndex{53}$

اضرب باستخدام خاصية التوزيع:$(y-3)\left(y^{2}-5 y+2\right)$

إجابة

$y^{3}-8 y^{2}+17 y-6$

التمارين$\PageIndex{54}$

اضرب باستخدام خاصية التوزيع:$(x+4)\left(2 x^{2}-3 x+5\right)$

إجابة

$2 x^{3}+5 x^{2}-7 x+20$

الآن دعونا نفعل نفس الضرب باستخدام الطريقة الرأسية.

التمارين$\PageIndex{55}$

اضرب باستخدام الطريقة الرأسية:$(b+3)\left(2 b^{2}-5 b+8\right)$

إجابة

من الأسهل وضع متعدد الحدود بمصطلحات أقل في الأسفل لأننا نحصل على عدد أقل من المنتجات الجزئية بهذه الطريقة.

$(2b^2 − 5b + 8)$اضرب في 3.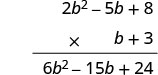
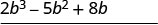
$(2b^2 − 5b + 8)$اضرب في$b$.	$2 b^{3}+b^{2}-7 b+24$
أضف مصطلحات الإعجاب.

التمارين$\PageIndex{56}$

اضرب باستخدام الطريقة الرأسية:$(y-3)\left(y^{2}-5 y+2\right)$

إجابة

$y^{3}-8 y^{2}+17 y-6$

التمارين$\PageIndex{57}$

اضرب باستخدام الطريقة الرأسية:$(x+4)\left(2 x^{2}-3 x+5\right)$

إجابة

$2 x^{3}+5 x^{2}-7 x+20$

لقد رأينا الآن طريقتين يمكنك استخدامهما لضرب ثلاثية الحدود في معادلة ذات حدين. بعد ممارسة كل طريقة، ربما ستجد أنك تفضل طريقة واحدة على الأخرى. نسرد كلتا الطريقتين مدرجتين هنا، لسهولة الرجوع إليها.

ضرب ثلاثية الحدود في معادلة ذات حدين

لضرب ثلاثية في معادلة ذات حدين، استخدم:

• خاصية التوزيع
• الطريقة الرأسية

ملاحظة

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية بضرب كثيرات الحدود:

• ضرب الأسس 1
• ضرب الأسس 2
• ضرب الأسس 3

المفاهيم الرئيسية

• طريقة FOIL لضرب اثنين من الحدين - لضرب اثنين من الحدود:
  1. اضرب المصطلحات الأولى.
  2. اضرب المصطلحات الخارجية.
  3. اضرب المصطلحات الداخلية.
  4. اضرب المصطلحات الأخيرة.
• ضرب اثنين من الحدين - لضرب اثنين من الحدود، استخدم:
  • خاصية التوزيع (مثال)
  • طريقة FOIL (مثال)
  • الطريقة الرأسية (مثال)
• ضرب ثلاثية الحدود في معادلة ذات حدين - لضرب ثلاثية في معادلة ذات حدين، استخدم:
  • خاصية التوزيع (مثال)
  • الطريقة الرأسية (مثال)