6.2: استخدم خصائص الضرب للأسس
- Page ID
- 200465
في نهاية هذا القسم، ستكون قادرًا على:
- قم بتبسيط التعبيرات باستخدام الأسس
- قم بتبسيط التعبيرات باستخدام خاصية المنتج للأسس
- قم بتبسيط التعبيرات باستخدام خاصية الطاقة للأسس
- قم بتبسيط التعبيرات باستخدام خاصية المنتج إلى الطاقة
- قم بتبسيط التعبيرات بتطبيق العديد من الخصائص
- اضرب وحيدات الحدود
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- التبسيط:\(\frac{3}{4}\cdot \frac{3}{4}\)
إذا فاتتك هذه المشكلة، راجع التمرين 1.6.13. - قم بالتبسيط:\((−2)(−2)(−2)\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.5.13.
قم بتبسيط التعبيرات باستخدام الأسس
تذكر أن الأس يشير إلى الضرب المتكرر لنفس الكمية. على سبيل المثال،\(2^4\) يعني نتاج\(4\) عوامل\(2\)، لذلك\(2^4\) يعني\(2·2·2·2\).
دعونا نراجع مفردات التعبيرات ذات الأسس.
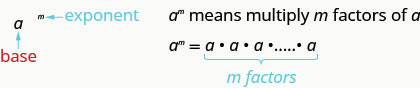
يتم قراءة\(a\) هذا\(m^{th}\) للسلطة.
في التعبير\(a^{m}\)،\(m\) يخبرنا الأس بعدد المرات التي نستخدم فيها القاعدة a كعامل.

قبل أن نبدأ العمل مع التعبيرات المتغيرة التي تحتوي على أسس، دعونا نبسط بعض التعبيرات التي تتضمن الأرقام فقط.
قم بالتبسيط:
- \(4^{3}\)
- \(7^{1}\)
- \(\left(\frac{5}{6}\right)^{2}\)
- \((0.63)^{2}\)
- إجابة
-
- \(\begin{array}{ll} & 4^{3}\\ {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\ {\text { Simplify. }} & {64}\end{array}\)
- \(\begin{array}{ll} & 7^{1}\\ \text{Multiply one factor of 7.} & 7\end{array}\)
- \(\begin{array}{ll} &\left(\frac{5}{6}\right)^{2}\\ {\text { Multiply two factors. }} & {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\ {\text { Simplify. }} & {\frac{25}{36}}\end{array}\)
- \(\begin{array}{ll} &(0.63)^{2}\\ {\text { Multiply two factors. }} & {(0.63)(0.63)} \\ {\text { Simplify. }} & {0.3969}\end{array}\)
قم بالتبسيط:
- \(6^{3}\)
- \(15^{1}\)
- \(\left(\frac{3}{7}\right)^{2}\)
- \((0.43)^{2}\)
- إجابة
-
- 216
- 15
- \(\frac{9}{49}\)
- 0.1849
قم بالتبسيط:
- \(2^{5}\)
- \(21^{1}\)
- \(\left(\frac{2}{5}\right)^{3}\)
- \((0.218)^{2}\)
- إجابة
-
- 32
- 21
- \(\frac{8}{125}\)
- 0.047524
قم بالتبسيط:
- \((-5)^{4}\)
- \(-5^{4}\)
- إجابة
-
- \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
- \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)
لاحظ أوجه التشابه والاختلاف في\(\PageIndex{4}\) الجزء الأول من المثال\(\PageIndex{4}\) والجزء الثاني من المثال! لماذا تختلف الإجابات؟ عندما نتبع ترتيب العمليات في الجزء 1، تخبرنا الأقواس برفعها\((−5)\) إلى القوة الرابعة. في الجزء 2، نرفع القوة\(5\) إلى القوة الرابعة فقط ثم نأخذ العكس.
قم بالتبسيط:
- \((-3)^{4}\)
- \(-3^{4}\)
- إجابة
-
- 81
- −81
قم بالتبسيط:
- \((-13)^{4}\)
- \(-13^{4}\)
- إجابة
-
- 169
- −169
قم بتبسيط التعبيرات باستخدام خاصية المنتج للأسس
لقد رأيت أنه عند دمج المصطلحات المتشابهة عن طريق الجمع والطرح، يجب أن يكون لديك نفس الأساس بنفس الأس. ولكن عندما تقوم بالضرب والقسمة، قد تكون الأسس مختلفة، وأحيانًا قد تكون القواعد مختلفة أيضًا.
سنقوم باستخلاص خصائص الأسس من خلال البحث عن الأنماط في عدة أمثلة.
أولاً، سننظر إلى مثال يؤدي إلى خاصية المنتج.
 |
|
| ماذا يعني هذا؟ كم عدد العوامل إجمالاً؟ |
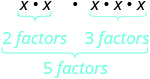 |
| لذلك، لدينا | 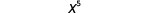 |
| لاحظ أن 5 هو مجموع الأسس، 2 و3. | 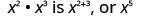 |
نحن نكتب:\[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]
بقيت القاعدة كما هي وأضفنا الأسس. يؤدي هذا إلى خاصية المنتج الخاصة بالأسس.
إذا كان\(a\) رقمًا حقيقيًا،\(m\)\(n\) ويتم حساب الأرقام، إذن
\[a^{m} \cdot a^{n}=a^{m+n}\]
للضرب باستخدام القواعد المتشابهة، قم بإضافة الأسس.
يساعد مثال بالأرقام في التحقق من هذه الخاصية.
\[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]
قم بالتبسيط:\(y^{5} \cdot y^{6}\)
- إجابة
-
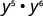
استخدم خاصية المنتج،\(a^{m} \cdot a^{n}=a^{m+n}\). 
قم بالتبسيط. 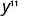
قم بالتبسيط:\(b^{9} \cdot b^{8}\)
- إجابة
-
\(b^{17}\)
قم بالتبسيط:\(x^{12} \cdot x^{4}\)
- إجابة
-
\(x^{16}\)
قم بالتبسيط:
- \(2^{5} \cdot 2^{9}\)
- \(3\cdot 3^{4}\)
- إجابة
-
أ.

استخدم خاصية المنتج،\(a^{m} \cdot a^{n}=a^{m+n}\). 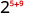
قم بالتبسيط. 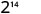
ب.
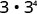
استخدم خاصية المنتج،\(a^{m} \cdot a^{n}=a^{m+n}\). 
قم بالتبسيط. 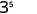
قم بالتبسيط:
- \(5\cdot 5^{5}\)
- \(4^{9} \cdot 4^{9}\)
- إجابة
-
- \(5^{6}\)
- \(4^{18}\)
قم بالتبسيط:
- \(7^{6} \cdot 7^{8}\)
- \(10 \cdot 10^{10}\)
- إجابة
-
- \(7^{14}\)
- \(10^{11}\)
قم بالتبسيط:
- \(a^{7} \cdot a\)
- \(x^{27} \cdot x^{13}\)
- إجابة
-
أ.
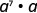
أعد كتابة،\(a = a^1\) 
استخدم خاصية المنتج،\(a^m\cdot a^n = a^{m+n}\). 
قم بالتبسيط. 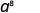
ب.

لاحظ أن القواعد هي نفسها، لذا أضف الأسس. 
قم بالتبسيط. 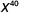
قم بالتبسيط:
- \(p^{5} \cdot p\)
- \(y^{14} \cdot y^{29}\)
- إجابة
-
- \(p^{6}\)
- \(y^{43}\)
قم بالتبسيط:
- \(z \cdot z^{7}\)
- \(b^{15} \cdot b^{34}\)
- إجابة
-
- \(z^{8}\)
- \(b^{49}\)
يمكننا توسيع خاصية المنتج لـ Exponents إلى أكثر من عاملين.
قم بالتبسيط:\(d^{4} \cdot d^{5} \cdot d^{2}\)
- إجابة
-
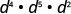
أضف الأسس، لأن القواعد هي نفسها. 
قم بالتبسيط. 
قم بالتبسيط:\(x^{6} \cdot x^{4} \cdot x^{8}\)
- إجابة
-
\(x^{18}\)
قم بالتبسيط:\(b^{5} \cdot b^{9} \cdot b^{5}\)
- إجابة
-
\(b^{19}\)
قم بتبسيط التعبيرات باستخدام خاصية القوة للأسس
لننظر الآن إلى تعبير أسي يحتوي على قوة مرفوعة إلى قوة. تحقق مما إذا كان بإمكانك اكتشاف عقار عام.
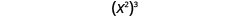 |
|
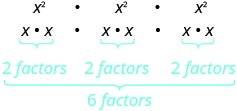
| ماذا يعني هذا؟ كم عدد العوامل إجمالاً؟ |
 |
| لذلك لدينا | 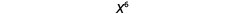 |
| لاحظ أن الرقم 6 هو حاصل ضرب الأسس، 2 و3. | 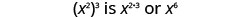 |
نحن نكتب:
\[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]
لقد ضربنا الأسس. يؤدي هذا إلى خاصية الطاقة للأسس.
\(a\)إذا كان رقمًا حقيقيًا،\(m\)\(n\) وعددًا صحيحًا، إذن
\[\left(a^{m}\right)^{n}=a^{m \cdot n}\]
لرفع قوة إلى قوة، اضرب الأسس.
يساعد مثال بالأرقام في التحقق من هذه الخاصية.
\[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]
قم بالتبسيط:
- \(\left(y^{5}\right)^{9}\)
- \(\left(4^{4}\right)^{7}\)
- إجابة
-
أ.
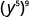
استخدم خاصية الطاقة،\(\big(a^m\big)^n = a^{m\cdot n}\). 
قم بالتبسيط. 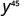
ب.
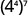
استخدم خاصية الطاقة. 
قم بالتبسيط. 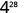
قم بالتبسيط:
- \( \left(b^{7}\right)^{5} \)
- \(\left(5^{4}\right)^{3}\)
- إجابة
-
- \( b^{35}\)
- \(5^{12}\)
قم بالتبسيط:
- \(\left(z^{6}\right)^{9}\)
- \(\left(3^{7}\right)^{7}\)
- إجابة
-
- \(z^{54}\)
- \(3^{49}\)
قم بتبسيط التعبيرات باستخدام المنتج إلى خاصية الطاقة
سننظر الآن في تعبير يحتوي على منتج تم رفعه إلى قوة. هل يمكنك العثور على هذا النمط؟
\(\begin{array}{ll}{\text { What does this mean? }} & {\text { (2x) }^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)
\(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)
ينطبق الأس على كل عامل من العوامل! يؤدي هذا إلى تحويل المنتج إلى خاصية الطاقة للأسس.
إذا كانت\(a\)\(b\) الأرقام حقيقية وكانت\(m\) عبارة عن رقم صحيح، إذن
\[(a b)^{m}=a^{m} b^{m}\]
لرفع المنتج إلى مستوى القوة، ارفع كل عامل إلى تلك القوة.
يساعد مثال بالأرقام في التحقق من هذه الخاصية:
\ [\ ابدأ {المصفوفة} {lll} (2\ النقطة 3) ^ {2}\ ستاكريل {؟} {=} &2^ {2}\ النقطة 3 ^ {2}\\ 6^ {2}\\ ستاكريل {؟} {=} &4\ cdot 9\\ 36 &=&=&36
\ علامة الاختيار\ النهاية {المصفوفة}\]
قم بالتبسيط:
- \((-9 d)^{2}\)
- \((3mn)^{3}\).
- إجابة
-
أ.
ب.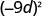
استخدم قوة خاصية المنتج،\((ab)^m=a^m b^m\). 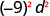
قم بالتبسيط. 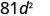
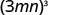
استخدم قوة خاصية المنتج،\((ab)^m=a^m b^m\). 
قم بالتبسيط. 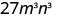
قم بالتبسيط:
- \((-12 y)^{2}\)
- \((2 w x)^{5}\)
- إجابة
-
- \(144y^{2}\)
- \(32w^{5} x^{5}\)
قم بالتبسيط:
- \((5 w x)^{3}\)
- \((-3 y)^{3}\)
- إجابة
-
- 125\(w^{3} x^{3}\)
- \(-27 y^{3}\)
قم بتبسيط التعبيرات بتطبيق العديد من الخصائص
لدينا الآن ثلاث خصائص لضرب التعبيرات باستخدام الأسس. دعونا نلخصها ثم سنقوم ببعض الأمثلة التي تستخدم أكثر من واحدة من الخصائص.
إذا كانت\(a\)\(b\) الأرقام حقيقية،\(m\) وما زالت أعدادًا\(n\) صحيحة، إذن
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
جميع خصائص الأس صحيحة لأي أرقام حقيقية\(m\) و\(n\). في الوقت الحالي، لا نستخدم سوى أسس الأرقام الكاملة.
قم بالتبسيط:
- \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
- \(\left(-6 x^{4} y^{5}\right)^{2}\)
- إجابة
-
- \(\begin{array}{ll}& \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\ {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\ {\text { Add the exponents. }} & y^{38} \end{array}\)
- \(\begin{array}{ll}& \left(-6 x^{4} y^{5}\right)^{2}\\ {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\ {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\ {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
قم بالتبسيط:
- \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
- \(\left(-2 c^{4} d^{2}\right)^{3}\)
- إجابة
-
- \(a^{48}\)
- \(-8 c^{12} d^{6}\)
قم بالتبسيط:
- \(\left(-3 x^{6} y^{7}\right)^{4}\)
- \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
- إجابة
-
- 81\(x^{24} y^{28}\)
- \(q^{29}\)
قم بالتبسيط:
- \((5 m)^{2}\left(3 m^{3}\right)\)
- \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
- إجابة
-
- \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
- \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
قم بالتبسيط:
- \((5 n)^{2}\left(3 n^{10}\right)\)
- \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
- إجابة
-
- 75\(n^{12}\)
- 81\(c^{24} d^{30}\)
قم بالتبسيط:
- \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
- \((2 x)^{3}\left(5 x^{7}\right)\)
- إجابة
-
- 256\(a^{22} b^{24}\)
- 40\(x^{10}\)
ضرب وحيدات الحدود
نظرًا لأن الحد الأحادي هو تعبير جبري، يمكننا استخدام خصائص الأسس لضرب وحيدات الحد.
اضرب:\(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)
- إجابة
-
\ (\ ابدأ {مصفوفة} {ll} &\ يسار (3 x^ {2}\ يمين)\ يسار (-4 x^ {3}\\ يمين)\\\ نص {استخدم خاصية الإبدال لإعادة ترتيب المصطلحات.} & 3\ cdot (-4)\ cdot x^ {2}\ cdot x^ {3}\\
\ النص {اضرب}. & -12 × ^ {5}\ النهاية {المصفوفة}\)
اضرب:\(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)
- إجابة
-
\(-35 y^{11}\)
اضرب:\(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)
- إجابة
-
54\(b^{9}\)
اضرب:\(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)
- إجابة
-
\(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)
اضرب:\(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)
- إجابة
-
6\(a^{5} b^{6}\)
اضرب:\(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)
- إجابة
-
8\(r^{11} s^{8}\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام خصائص الضرب الخاصة بالأسس:
- خصائص الضرب للأسس
المفاهيم الرئيسية
- الترميز الأسي
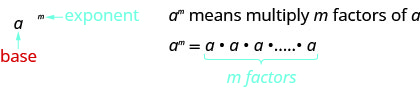
- خصائص الأسس
- إذا كانت\(a\)\(b\) الأرقام حقيقية\(m\) وما زالت أرقامًا\(n\) صحيحة، إذن
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]


