5.2: حل أنظمة المعادلات بالتعويض
- Page ID
- 200103
في نهاية هذا القسم، ستكون قادرًا على:
- حل نظام المعادلات عن طريق الاستبدال
- حل تطبيقات أنظمة المعادلات عن طريق الاستبدال
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بتبسيط −5 (3−x).
إذا فاتتك هذه المشكلة، راجع التمرين 1.10.43. - قم بتبسيط 4−2 (n+5).
إذا فاتتك هذه المشكلة، راجع التمرين 1.10.41. - حل لـ y. 8y−8=32-2y
إذا فاتتك هذه المشكلة، راجع التمرين 2.3.22. - حل لـ x. 3x−9y=−3
إذا فاتتك هذه المشكلة، راجع التمرين 2.6.22.
يعد حل أنظمة المعادلات الخطية بالرسوم البيانية طريقة جيدة لتصور أنواع الحلول التي قد تنتج. ومع ذلك، هناك العديد من الحالات التي يكون فيها حل النظام عن طريق الرسوم البيانية غير مريح أو غير دقيق. إذا كانت الرسوم البيانية تمتد إلى ما وراء الشبكة الصغيرة بحيث يكون x وy كلاهما بين −10 و10، فقد يكون التمثيل البياني للخطوط مرهقًا. وإذا لم تكن حلول النظام عبارة عن أعداد صحيحة، فقد يكون من الصعب قراءة قيمها بدقة من الرسم البياني.
في هذا القسم، سنحل أنظمة المعادلات الخطية بطريقة الاستبدال.
حل نظام المعادلات بالتعويض
سنستخدم نفس النظام الذي استخدمناه أولاً للرسم البياني.
\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
سنحل أولاً إحدى المعادلات الخاصة بـ x أو y. يمكننا اختيار أي من المعادلتين وحل أي من المتغيرين - لكننا سنحاول اتخاذ خيار من شأنه أن يجعل العمل سهلاً.
ثم نستبدل هذا التعبير بالمعادلة الأخرى. والنتيجة هي معادلة بمتغير واحد فقط - ونحن نعرف كيفية حلها!
بعد العثور على قيمة متغير واحد، سنقوم باستبدال هذه القيمة بإحدى المعادلات الأصلية وحل المتغير الآخر. أخيرًا، نتحقق من حلنا ونتأكد من صحة المعادلتين.
سنقوم بملء كل هذه الخطوات الآن في التمرين\(\PageIndex{1}\).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- إجابة
-






حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)
- إجابة
-
(6,1)
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)
- إجابة
-
(4,2)
- حل إحدى المعادلات لأي متغير.
- استبدل التعبير من الخطوة 1 بالمعادلة الأخرى.
- حل المعادلة الناتجة.
- استبدل الحل في الخطوة 3 بإحدى المعادلات الأصلية للعثور على المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.
إذا كانت إحدى المعادلات في النظام معطاة في شكل منحدر - تقاطع، تكون الخطوة 1 قد أُنجزت بالفعل! سنرى هذا في التمرين\(\PageIndex{4}\).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)
- إجابة
-
تم حل المعادلة الثانية بالفعل لـ y. سنستبدل التعبير بدلاً من y في المعادلة الأولى.
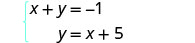
تم حل المعادلة الثانية بالفعل لـ y.
سنستبدل المعادلة الأولى.استبدل y بـ x + 5. 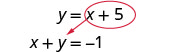
حل المعادلة الناتجة لـ x. 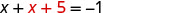
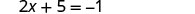
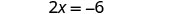
استبدل x = −3 إلى y = x + 5 للعثور على y. 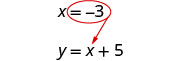
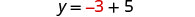
الزوج الذي تم ترتيبه هو (−3، 2). 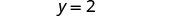
تحقق من الزوج المرتب في كلتا المعادلتين:
\(\begin{array} {rllrll} x+y &=&-1 & y&=&x+5\\-3+2 &\stackrel{?}{=}&-1 &2& \stackrel{?}{=} & -3 + 5\\-1 &=&-1\checkmark &2 &=&2\checkmark \end{array}\)الحل هو (−3، 2).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)
- إجابة
-
(2,4)
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)
- إجابة
-
(−1، −3)
إذا تم إعطاء المعادلات في الشكل القياسي، سنحتاج إلى البدء بحل أحد المتغيرات. في هذا المثال التالي، سنحل المعادلة الأولى لـ y.
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)
- إجابة
-
نحن بحاجة إلى حل معادلة واحدة لمتغير واحد. ثم سنستبدل هذا التعبير بالمعادلة الأخرى.
حل من أجلك.
استبدل المعادلة الأخرى.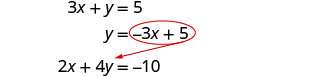
استبدل y بـ −3 x + 5. 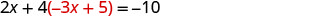
حل المعادلة الناتجة لـ x. 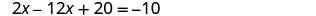
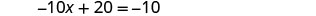
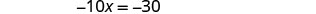
استبدل x = 3 إلى 3 x + y = 5 للعثور على y. 


الزوج الذي تم ترتيبه هو (3، −4). 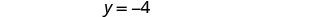
تحقق من الزوج المرتب في كلتا المعادلتين:
\(\begin{array} {rllrll} 3x+y &=&5 & 2x+4y&=&-10\\3\cdot3+(-4) &\stackrel{?}{=}&5 &2\cdot3 + 4(-4)& \stackrel{?}{=} & -10\\9-4&\stackrel{?}{=}&5 &6-16& \stackrel{?}{=} & -10\\5 &=&5\checkmark &-10&=&-10\checkmark \end{array}\)الحل هو (3، −4).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)
- إجابة
-
(1، −2)
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)
- إجابة
-
(2,6)
في التمرين\(\PageIndex{7}\)، كان من الأسهل حل y في المعادلة الأولى لأنه يحتوي على معامل 1. في التمرين\(\PageIndex{10}\)، سيكون من الأسهل حل x.
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)
- إجابة
-
سنحل المعادلة الأولى لـ xx ثم نستبدل التعبير بالمعادلة الثانية.

حل لـ x.
استبدل المعادلة الأخرى.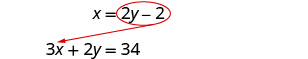
استبدل x بـ 2 y − 2. 
حل المعادلة الناتجة لـ y. 
استبدل y = 5 إلى x − 2 y = −2 لإيجاد x.

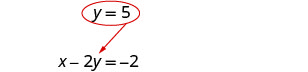



الزوج المطلوب هو (8، 5). تحقق من الزوج المرتب في كلتا المعادلتين:
\(\begin{array} {rllrll} x-2y &=&-2 & 3x+2y&=&34\\8-2\cdot 5 &\stackrel{?}{=}&-2 &3\cdot8 + 2\cdot5& \stackrel{?}{=} & 34\\8-10&\stackrel{?}{=}&-2 &24+10& \stackrel{?}{=} & 34\\-2 &=&-2\checkmark &34&=&34\checkmark \end{array}\)الحل هو (8، 5).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)
- إجابة
-
(−2، −3)
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)
- إجابة
-
(6,2)
عندما يتم حل كلتا المعادلتين بالفعل لنفس المتغير، فمن السهل استبدالهما!
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- إجابة
-
نظرًا لأن كلتا المعادلتين قد تم حلهما لـ y، فيمكننا استبدال إحداهما بالأخرى.
استبدل\(\frac{1}{2}x\) y في المعادلة الأولى. 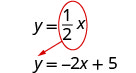
استبدل y بـ\(\frac{1}{2}x\) 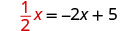
حل المعادلة الناتجة.
ابدأ بمسح الكسر.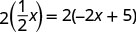
حل لـ x. 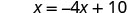
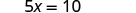
استبدل x = 2\(y = \frac{1}{2}x\) للعثور على y. 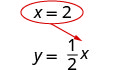
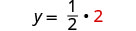
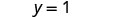
الزوج المطلوب هو (2,1). تحقق من الزوج المرتب في كلتا المعادلتين:
\(\begin{array} {rllrll} y &=&\frac{1}{2}x & y&=&-2x+5\\1 &\stackrel{?}{=}&\frac{1}{2}\cdot2 &1& \stackrel{?}{=} & -2\cdot2+5\\1 &=&1\checkmark &1 &=&-4+5\\ &&&1&=&1\checkmark \end{array}\)الحل هو (2,1).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)
- إجابة
-
(6,2)
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)
- إجابة
-
(8,2)
كن حذرًا جدًا مع العلامات الموجودة في المثال التالي.
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)
- إجابة
-
نحن بحاجة إلى حل معادلة واحدة لمتغير واحد. سنحل المعادلة الأولى لـ y.

حل المعادلة الأولى لـ y. 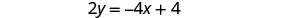
استبدل −2 x + 2 عن y في المعادلة الثانية. 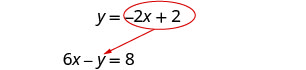
استبدل y بـ −2 x + 2. 
حل المعادلة لـ x. 


استبدل\(x = \frac{5}{4}\) 4 × + 2 ص = 4 للعثور على y.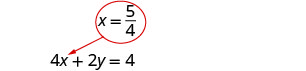



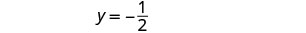
الزوج المطلوب هو\((\frac{5}{4},−\frac{1}{2})\). تحقق من الزوج المرتب في كلتا المعادلتين.
\(\begin{array} {rllrll} 4x+2y &=&4& 6x-y&=&8\\4(\frac{5}{4}) +2(-\frac{1}{2})&\stackrel{?}{=}&4 &6(\frac{5}{4}) - (-\frac{1}{2})& \stackrel{?}{=} & 8\\5-1&\stackrel{?}{=}&4 &\frac{15}{4} - (-\frac{1}{2}) &\stackrel{?}{=} & 8\\4 &=&4\checkmark &\frac{16}{2} &\stackrel{?}{=}&8\\ &&&8&=&8\checkmark \end{array}\)الحل هو (54، −12).
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
- إجابة
-
\((2,\frac{3}{2})\)
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)
- إجابة
-
\((−\frac{1}{2},−2)\)
على سبيل المثال، سوف يستغرق الأمر المزيد من العمل لحل معادلة واحدة لـ x أو y.
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)
- إجابة
-
نحن بحاجة إلى حل معادلة واحدة لمتغير واحد. سنحل المعادلة الأولى لـ x.
نظرًا لأن 0 = 0 عبارة صحيحة، فإن النظام ثابت. تعتمد المعادلات. تعطي الرسوم البيانية لهاتين المعادلتين نفس الخط. يحتوي النظام على العديد من الحلول بلا حدود.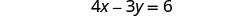
حل المعادلة الأولى لـ x. 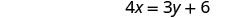
استبدل\(\frac{3}{4} y+\frac{3}{2}\) x في المعادلة الثانية. 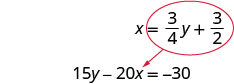
استبدل x بـ\(\frac{3}{4} y+\frac{3}{2}\) 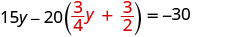
حل من أجلك. 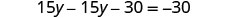
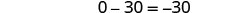

حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)
- إجابة
-
العديد من الحلول بلا حدود
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)
- إجابة
-
العديد من الحلول بلا حدود
انظر إلى المعادلات في التمرين\(\PageIndex{22}\). هل هناك أي طريقة للتعرف على أنهم نفس الخط؟
دعونا نرى ما يحدث في المثال التالي.
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)
- إجابة
-
تم حل المعادلة الثانية بالفعل لـ y، لذا يمكننا استبدال y في المعادلة الأولى.
نظرًا لأن 0 = −10 عبارة خاطئة، فإن المعادلات غير متناسقة. ستكون الرسوم البيانية للمعادلتين عبارة عن خطوط متوازية. لا يحتوي النظام على حلول.استبدل x بـ y في المعادلة الأولى. 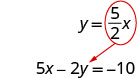
استبدل y بـ\(\frac{5}{2}x\). 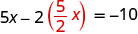
حل لـ x. 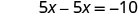

حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل النظام عن طريق الاستبدال. \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل تطبيقات أنظمة المعادلات بالتعويض
سننسخ هنا استراتيجية حل المشكلات التي استخدمناها في قسم حل أنظمة المعادلات عن طريق الرسوم البيانية لحل أنظمة المعادلات. الآن بعد أن عرفنا كيفية حل الأنظمة عن طريق الاستبدال، هذا ما سنفعله في الخطوة 5.
- اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
- حدد ما نبحث عنه.
- اذكر ما نبحث عنه. اختر المتغيرات لتمثيل تلك الكميات.
- ترجم إلى نظام المعادلات.
- حل نظام المعادلات باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
يجد بعض الأشخاص أن إعداد مشاكل الكلمات بمتغيرين أسهل من إعدادها باستخدام متغير واحد فقط. يكون اختيار أسماء المتغيرات أسهل عندما يكون كل ما عليك فعله هو كتابة حرفين. فكر في هذا في المثال التالي - كيف كنت ستفعل ذلك باستخدام متغير واحد فقط؟
مجموع الرقمين هو صفر. رقم واحد أقل بتسعة من الآخر. ابحث عن الأرقام.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن رقمين. الخطوة 3. اذكر ما نبحث عنه. Let n= الرقم الأول
دع m= الرقم الثانيالخطوة 4. ترجم إلى نظام من المعادلات. مجموع الرقمين هو صفر. 
رقم واحد أقل بتسعة من الآخر. 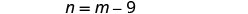
النظام هو: 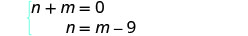
الخطوة 5. حل نظام
المعادلات. سنستخدم الاستبدال
حيث تم حل المعادلة الثانية
لـ n.استبدل m − 9 عن n في المعادلة الأولى. 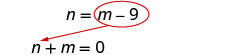
حل بالنسبة لي. 


استبدل\(m=\frac{9}{2}\) المعادلة الثانية
ثم قم بحل n.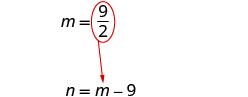
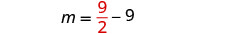
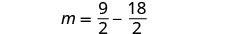
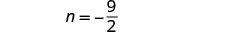
الخطوة 6. تحقق من الإجابة في المشكلة. هل هذه الأرقام منطقية في
المشكلة؟ سنترك هذا لك!الخطوة 7. أجب على السؤال. الأرقام هي\(\frac{9}{2}\) و\(-\frac{9}{2}\).
مجموع الرقمين هو 10. رقم واحد أقل بأربعة من الآخر. ابحث عن الأرقام.
- إجابة
-
الأرقام هي 3 و 7.
مجموع العددين هو −6. رقم واحد أقل بعشرة من الآخر. ابحث عن الأرقام.
- إجابة
-
الأرقام هي 2 و−8.
في التمرين\(\PageIndex{28}\)، سنستخدم صيغة محيط المستطيل، P = 2 L + 2 W.
أضف نصًا للتمارين هنا.
- إجابة
-
الخطوة 1. اقرأ المشكلة. 
الخطوة 2. حدد ما تبحث عنه. نحن نبحث عن الطول والعرض. الخطوة 3. اذكر ما نبحث عنه. دع L = الطول
W = العرضالخطوة 4. ترجم إلى نظام من المعادلات. محيط المستطيل هو 88. 2 لتر+ 2 واط = P
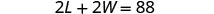
الطول يزيد بمقدار خمسة عن ضعف العرض. 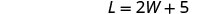
النظام هو: 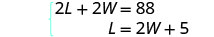
الخطوة 5. حل نظام المعادلات.
سنستخدم الاستبدال حيث تم حل
المعادلة الثانية لـ L.
استبدل 2 W + 5 عن L في المعادلة الأولى.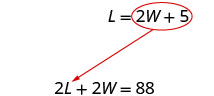
حل لـ W. 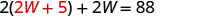
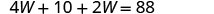
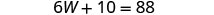
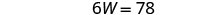
استبدل W = 13 في
المعادلة الثانية ثم قم بحل L.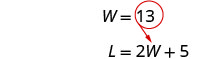
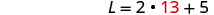
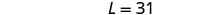
الخطوة 6. تحقق من الإجابة في المشكلة. هل مستطيل طوله ٣١ وعرضه
١٣ محيطه ٨٨؟ نعم.الخطوة 7. أجب على المعادلة. الطول هو 31 والعرض هو 13.
محيط المستطيل هو 40. الطول يزيد بمقدار 4 عن العرض. أوجد طول المستطيل وعرضه.
- إجابة
-
الطول هو 12 والعرض هو 8.
محيط المستطيل هو 58. الطول يزيد بمقدار 5 أضعاف عن العرض بثلاثة أضعاف. أوجد طول المستطيل وعرضه.
- إجابة
-
الطول هو 23 والعرض هو 6.
للتمرين،\(\PageIndex{31}\) علينا أن نتذكر أن مجموع قياسات زوايا المثلث هو 180 درجة وأن المثلث الأيمن له زاوية واحدة 90 درجة.
قياس إحدى الزوايا الصغيرة للمثلث القائم يزيد بمقدار عشرة أضعاف عن قياس الزاوية الصغيرة الأخرى بمقدار عشرة أضعاف. أوجد قياسات كلتا الزاويتين.
- إجابة
-
سنقوم برسم وتسمية شخصية.
الخطوة 1. اقرأ المشكلة. 
الخطوة 2. حدد ما تبحث عنه. نحن نبحث عن مقاييس الزوايا. الخطوة 3. اذكر ما نبحث عنه. دعونا a = قياس الزاوية الأولى
b = قياس الزاوية الثانيةالخطوة 4. ترجم إلى نظام من المعادلات. قياس إحدى الزوايا الصغيرة للمثلث
القائم يزيد بمقدار عشرة
أضعاف عن قياس الزاوية الصغيرة الأخرى بمقدار عشرة أضعاف.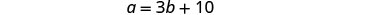
مجموع قياسات زوايا المثلث
هو 180.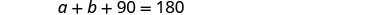
النظام هو: 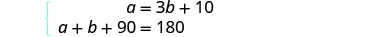
الخطوة 5. حل نظام المعادلات.
سنستخدم الاستبدال حيث تم حل
المعادلة الأولى لـ a.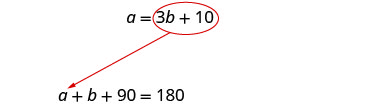
استبدل 3 b + 10 بـ a في المعادلة
الثانية.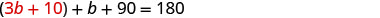
حل لـ ب. 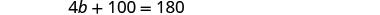


استبدل b = 20 في
المعادلة الأولى ثم قم بحل a.

الخطوة 6. تحقق من الإجابة في المشكلة. سنترك هذا لك! الخطوة 7. أجب على السؤال. مقاييس الزوايا الصغيرة هي
20 و 70.
يزيد قياس إحدى الزوايا الصغيرة للمثلث الأيمن بمقدار 2 عن 3 أضعاف قياس الزاوية الصغيرة الأخرى. أوجد قياس كلتا الزاويتين.
- إجابة
-
قياس الزوايا هو 22 درجة و 68 درجة.
يقل قياس إحدى الزوايا الصغيرة للمثلث القائم الزاوية بمقدار ١٨ عن ضعف قياس الزاوية الصغيرة الأخرى. أوجد قياس كلتا الزاويتين.
- إجابة
-
قياس الزوايا هو 36 درجة و 54 درجة.
عُرض على هيذر خياران مقابل راتبها كمدربة في صالة الألعاب الرياضية. الخيار أ سيدفع لها 25,000 دولار بالإضافة إلى 15 دولارًا لكل جلسة تدريبية. الخيار ب سيدفع لها 10,000 دولار + 40 دولارًا لكل جلسة تدريبية. كم عدد الدورات التدريبية التي ستجعل خيارات الراتب متساوية؟
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. نحن نبحث عن عدد الدورات التدريبية التي من شأنها
أن تجعل الأجر متساويًا.الخطوة 3. اذكر ما نبحث عنه. Let s= راتب هيذر.
n = عدد الدورات التدريبيةالخطوة 4. ترجم إلى نظام من المعادلات. الخيار أ سيدفع لها 25,000 دولار بالإضافة إلى 15 دولارًا
لكل جلسة تدريبية.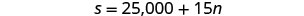
الخيار ب سيدفع لها 10,000 دولار + 40 دولارًا
لكل جلسة تدريبية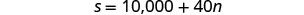
النظام هو: 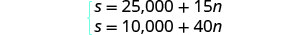
الخطوة 5. حل نظام المعادلات.
سوف نستخدم الاستبدال.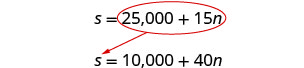
استبدل 25,000 + 15 n عن s في المعادلة الثانية. 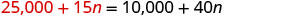
حل لـ n. 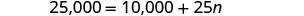
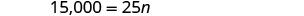

الخطوة 6. تحقق من الإجابة. هل 600 دورة تدريبية في السنة معقولة؟
هل الخياران متساويان عندما n = 600؟الخطوة 7. أجب على السؤال. ستكون خيارات الراتب متساوية لـ 600 دورة تدريبية.
تم عرض وظائف على Geraldine من قبل شركتين للتأمين. تدفع الشركة الأولى راتبًا قدره 12,000 دولار بالإضافة إلى عمولة قدرها 100 دولار لكل بوليصة يتم بيعها. يدفع الثاني راتبًا قدره 20,000 دولار بالإضافة إلى عمولة قدرها 50 دولارًا لكل بوليصة يتم بيعها. كم عدد السياسات التي يجب بيعها لجعل إجمالي الأجر هو نفسه؟
- إجابة
-
يجب بيع 160 بوليصة لجعل إجمالي الأجر هو نفسه.
يبيع كينيث حاليًا بدلات للشركة A براتب قدره 22,000 دولار بالإضافة إلى عمولة 10 دولارات لكل بدلة يتم بيعها. تقدم له الشركة B منصبًا براتب 28,000 دولار بالإضافة إلى عمولة 4 دولارات لكل بدلة يتم بيعها. كم عدد الدعاوى التي سيحتاج كينيث إلى بيعها حتى تتساوى الخيارات؟
- إجابة
-
سيحتاج كينيث إلى بيع 1000 بدلة.
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل أنظمة المعادلات عن طريق الاستبدال.
المفاهيم الرئيسية
- حل نظام المعادلات عن طريق الاستبدال
- حل إحدى المعادلات لأي متغير.
- استبدل التعبير من الخطوة 1 بالمعادلة الأخرى.
- حل المعادلة الناتجة.
- استبدل الحل في الخطوة 3 بإحدى المعادلات الأصلية للعثور على المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.


