Skip to main content
Global

5.5: حل تطبيقات المزيج باستخدام أنظمة المعادلات

  1. Last updated
  2. Save as PDF
  • Page ID
    200134

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • حل تطبيقات الخليط
    • حل تطبيقات الاهتمام
    ملاحظة

    قبل البدء، قم بإجراء اختبار الجاهزية هذا.

    1. اضرب 4.025 (1,562).
      إذا فاتتك هذه المشكلة، راجع التمرين 1.8.22.
    2. اكتب 8.2% في صورة عدد عشري.
      إذا فاتتك هذه المشكلة، راجع التمرين 1.8.46.
    3. وصلت فاتورة عشاء إيرل إلى 32.50 دولارًا وأراد ترك إكرامية بنسبة 18٪. كم يجب أن تكون الإكرامية؟
      إذا فاتتك هذه المشكلة، راجع التمرين 3.2.10.

    حل تطبيقات المزيج

    عندما قمنا بحل تطبيقات المزيج باستخدام العملات المعدنية والتذاكر سابقًا، بدأنا بإنشاء جدول حتى نتمكن من تنظيم المعلومات. للحصول على مثال للعملات المعدنية بالنيكل والديمات، بدا الجدول كما يلي:

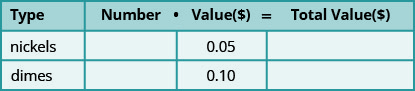
    هذا جدول يحتوي على ثلاثة صفوف وأربعة أعمدة. الصف الأول من الجدول هو صف العنوان، وتقوم كل خلية بتسمية العمود أو الأعمدة الموجودة أسفله. تسمى الخلية الأولى من اليسار «النوع». تحتوي الخلية الثانية على معادلة «الرقم» في «القيمة» تساوي «القيمة الإجمالية»، مع عمود واحد مقابل «الرقم»، وعمود واحد مقابل «القيمة»، وعمود واحد يتوافق مع القيمة الإجمالية. ومن ثم فإن محتوى عمود «الرقم» مضروبًا في محتوى عمود «القيمة» يساوي محتوى عمود «القيمة الإجمالية». في الصف الثاني من الجدول، يحتوي عمود «النوع» على «النيكل»، وعمود «الرقم» فارغ، وعمود «القيمة» يحتوي على 0.05، وعمود «القيمة الإجمالية» فارغ. في الصف الثالث من الجدول، يحتوي عمود «النوع» على «الدايمات»، وعمود «الرقم» فارغ، وعمود «القيمة يحتوي على 0.10، وعمود «القيمة الإجمالية» فارغ.

    استخدام متغير واحد يعني أنه كان علينا ربط عدد النيكل وعدد الدايمات. كان علينا أن نقرر ما إذا كنا سنسمح لـ n بأن يكون عدد النيكل ثم نكتب عدد الدايمات بدلالة n، أو ما إذا كنا سنسمح لـ d بأن يكون عدد الدايمات ونكتب عدد النيكل بدلالة d.

    الآن بعد أن عرفنا كيفية حل أنظمة المعادلات بمتغيرين، سنجعل n هو عدد النيكل و d هو عدد الدايمات. سنكتب معادلة واحدة استنادًا إلى عمود القيمة الإجمالية، كما فعلنا من قبل، وستأتي المعادلة الأخرى من عمود الأرقام.

    بالنسبة للمثال الأول، سنقوم بحل مشكلة التذاكر حيث تكون أسعار التذاكر بالدولار بالكامل، لذلك لن نحتاج إلى استخدام الأرقام العشرية حتى الآن.

    التمارين الرياضية\(\PageIndex{1}\)

    ترجم إلى نظام المعادلات وقم بحلها:

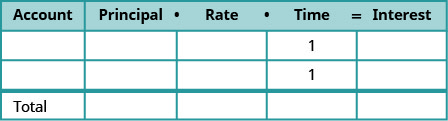
    باع شباك التذاكر في إحدى دور السينما 147 تذكرة للعرض المسائي، وبلغ إجمالي الإيصالات 1,302 دولارًا. كم عدد تذاكر البالغين البالغة 11 دولارًا وعدد تذاكر الأطفال التي تم بيعها بقيمة 8 دولارات؟

    إجابة
    الخطوة 1. اقرأ المشكلة. سننشئ جدولًا لتنظيم المعلومات.
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن عدد تذاكر
    البالغين وعدد تذاكر الأطفال المباعة.
    الخطوة 3. اذكر ما نبحث عنه. دعونا = عدد تذاكر البالغين.
    c = عدد تذاكر الأطفال
    سيساعدنا الجدول في تنظيم البيانات.
    لدينا نوعان من التذاكر: للبالغين والأطفال.    		 اكتب a و c لعدد التذاكر.
    اكتب العدد الإجمالي للتذاكر المباعة في
    أسفل عمود الرقم.    		 تم بيع 147 إجمالاً.
    اكتب قيمة كل نوع من التذاكر في عمود
    القيمة.    		 تبلغ قيمة كل تذكرة للبالغين 11 دولارًا.
    تبلغ قيمة تذاكر كل طفل 8 دولارات.
    عدد مرات القيمة يعطي
    القيمة الإجمالية، وبالتالي فإن القيمة الإجمالية لتذاكر البالغين هي
    \(a\cdot 11=11a\)، والقيمة الإجمالية
    لتذاكر الأطفال هي\(c\cdot 8=8c\).    		 .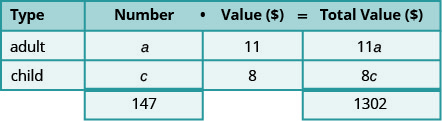
    وإجمالا، بلغت القيمة الإجمالية للتذاكر
    1,302 دولار.    		 املأ عمود القيمة الإجمالية.
    الخطوة 4. ترجم إلى نظام من المعادلات.  
    يعطينا عمود الرقم
    وعمود القيمة الإجمالية نظام المعادلات.
    سنستخدم طريقة الإزالة لحل
    هذا النظام.    		 .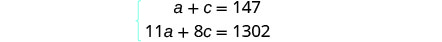
    اضرب المعادلة الأولى في −8. .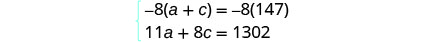
    قم بالتبسيط والإضافة، ثم قم بحل ملف.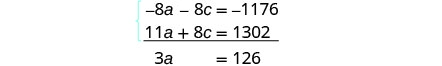

    مثال 5.45.JPG
      .
    استبدل a = 42 في المعادلة الأولى،
    ثم قم بحل c.    		 .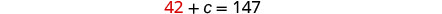
      .
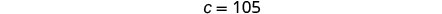
    الخطوة 5. تحقق من الإجابة في المشكلة.

    42 تذكرة للبالغين بسعر 11 دولارًا لكل تذكرة تجعل 462 دولارًا و
    105 تذاكر للأطفال بسعر 8 دولارات لكل تذكرة تبلغ 840 دولارًا.
    ويبلغ مجموع المبالغ المستلمة 302 1 دولاراً. ✓    		  
    الخطوة 6. أجب على السؤال. باعت دار السينما 42 تذكرة للبالغين و 105 تذكرة للأطفال.
    التمارين الرياضية\(\PageIndex{2}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    باع مكتب التذاكر في حديقة الحيوان 553 تذكرة في يوم واحد. بلغ إجمالي الإيصالات 3,936 دولارًا. كم عدد تذاكر البالغين بقيمة 9 دولارات وكم عدد تذاكر الأطفال التي تم بيعها بقيمة 6 دولارات؟

    إجابة

    تم بيع 206 تذكرة للبالغين وبيع 347 تذكرة للأطفال.

    التمارين الرياضية\(\PageIndex{3}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    باع مركز علمي 1363 تذكرة في عطلة نهاية أسبوع مزدحمة. وقد بلغ مجموع الإيرادات 146 12 دولارا. كم عدد تذاكر البالغين بقيمة 12 دولارًا وكم عدد تذاكر الأطفال التي تم بيعها بقيمة 7 دولارات؟

    إجابة

    تم بيع 521 تذكرة للبالغين وبيع 842 تذكرة للأطفال.

    في التمرين،\(\PageIndex{4}\) سنحل مشكلة العملة. الآن بعد أن عرفنا كيفية العمل مع أنظمة من متغيرين، ستكون تسمية المتغيرات في عمود «الرقم» سهلة.

    التمارين\(\PageIndex{4}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    تحتوي Priam على مجموعة من النيكل والأرباع بقيمة إجمالية قدرها 7.30 دولارًا. يقل عدد النيكل بستة أضعاف عن ثلاثة أضعاف عدد الأرباع. كم عدد النيكل وعدد الأرباع التي يمتلكها؟

    إجابة
    الخطوة 1. اقرأ المشكلة. سننشئ جدولًا لتنظيم المعلومات.
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن عدد النيكل
    وعدد الأرباع.
    الخطوة 3. اذكر ما نبحث عنه. Let n = عدد النيكل.
    q= عدد الأرباع
    سيساعدنا الجدول في تنظيم البيانات.
    لدينا نوعان من العملات المعدنية، النيكل
    والأرباع.    		 اكتب n و q لرقم كل نوع من أنواع العملات.
    املأ عمود القيمة بقيمة كل
    نوع من أنواع العملات.    		 قيمة كل نيكل هي 0.05 دولار.
    قيمة كل ربع سنة هي 0.25 دولار.
    يعطي الرقم مضروبًا في
    القيمة القيمة الإجمالية، لذا فإن القيمة الإجمالية للنيكل هي
    n (0.05) = 0.05 n والقيمة الإجمالية
    للأرباع هي q (0.25) = 0.25 q.
    تبلغ القيمة الإجمالية للعملات
    7.30 دولارًا.    		 .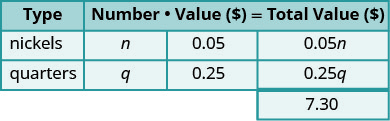
    الخطوة 4. ترجم إلى نظام من المعادلات.  
    يعطي عمود القيمة الإجمالية معادلة واحدة. .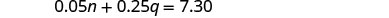
    نعلم أيضًا أن عدد النيكل
    أقل بستة من ثلاثة أضعاف عدد الأرباع.
    ترجم للحصول على المعادلة الثانية.    		 .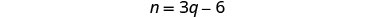
    الآن لدينا نظام لحلها. .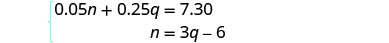
    الخطوة 5. حل نظام المعادلات
    سنستخدم طريقة الاستبدال.
    استبدل n = 3 q − 6 في المعادلة الأولى.
    قم بالتبسيط والحل لـ q.    		 .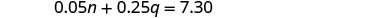
      .
      .
      .
      .
      .
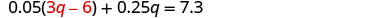
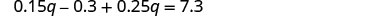
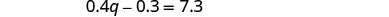
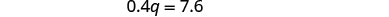
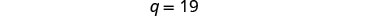
    لإيجاد عدد النيكل، استبدل
    q = 19 في المعادلة الثانية.    		 .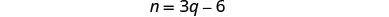
      .
      .
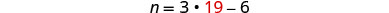
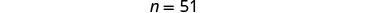
    الخطوة 6. تحقق من الإجابة في المشكلة.

    \(\begin{aligned} 19 \text { quarters at } \$ 0.25 &=\$ 4.75 \\ 51 \text { ickels at } \$ 0.05 &=\$ 2.55 \\ \text { Total } &=\$ 7.30 \checkmark \\ 3 \cdot 19-16 &=51 \checkmark\end{aligned}\)    		  
    الخطوة 7. أجب على السؤال. يحتوي بريام على 19 ربعًا و 51 نيكلًا.
    التمارين\(\PageIndex{5}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    تمتلك ماتيلدا حفنة من الأرباع والدايمات، بقيمة إجمالية تبلغ 8.55 دولارًا. عدد الأرباع يزيد بمقدار 3 عن ضعف عدد الدايمات. كم عدد الدايمات وكم عدد الأرباع التي تملكها؟

    إجابة

    لدى ماتيلدا 13 ديمًا و 29 ربعًا.

    التمارين\(\PageIndex{6}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    لدى خوان جيب مليء بالنيكل والديمات. القيمة الإجمالية للعملات هي 8.10 دولار. يقل عدد الدايمات بمقدار 9 سنتات عن ضعف عدد النيكل. كم عدد النيكل وعدد الدايمات التي يمتلكها خوان؟

    إجابة

    يمتلك خوان 36 نيكلًا و 63 ديمًا.

    تتضمن بعض تطبيقات الخلطات الجمع بين الأطعمة أو المشروبات. قد تتضمن أمثلة الحالات الجمع بين الزبيب والمكسرات لعمل مزيج سريع أو استخدام نوعين من حبوب البن لعمل مزيج.

    التمارين\(\PageIndex{7}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    يريد كارسون صنع 20 رطلاً من المزيج السريع باستخدام المكسرات ورقائق الشوكولاتة. تتطلب ميزانيته أن يكلفه مزيج الدرب 7.60 دولارًا للرطل. تبلغ تكلفة المكسرات 9.00 دولارًا للرطل، بينما تبلغ تكلفة رقائق الشوكولاتة 2.00 دولارًا للرطل. كم رطل من المكسرات وكم رطل من رقائق الشوكولاتة يجب أن يستخدمه؟

    إجابة
    الخطوة 1. اقرأ المشكلة. سننشئ جدولًا لتنظيم المعلومات.
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن عدد أرطال المكسرات
    وعدد أرطال رقائق الشوكولاتة.
    الخطوة 3. اذكر ما نبحث عنه. Let n = عدد رطل المكسرات.
    c = عدد أرطال الرقائق
    سيخلط كارسون المكسرات ورقائق الشوكولاتة
    للحصول على مزيج سريع.
    اكتب n و c لعدد أرطال
    المكسرات ورقائق الشوكولاتة.

    سيكون هناك 20 رطلاً من مزيج الطرق.
    ضع سعر الرطل لكل عنصر
    في عمود القيمة.
    املأ العمود الأخير باستخدام    		 .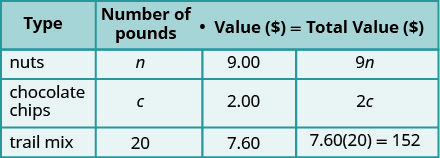
    الرقم · القيمة = القيمة الإجمالية  
    الخطوة 4. ترجم إلى نظام من المعادلات.
    نحصل على المعادلات من عمودي العدد
    والقيمة الإجمالية.    		 .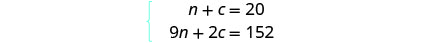
    الخطوة 5. حل نظام المعادلات
    سنستخدم الحذف لحل النظام.    		  
    اضرب المعادلة الأولى في −2 لإزالة c. .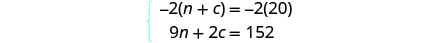
    قم بالتبسيط والإضافة. حل لـ n. .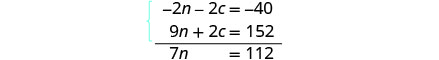
      .
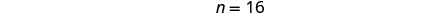
    لإيجاد عدد أرطال رقائق
    الشوكولاتة، استبدل n = 16 في
    المعادلة الأولى، ثم حل العدد c.    		 .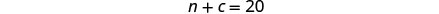
    .
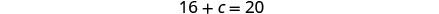
      ج = 4
    الخطوة 6. تحقق من الإجابة في المشكلة.

    \(\begin{aligned} 16+4 &=20 \checkmark \\ 9 \cdot 16+2 \cdot 4 &=152 \checkmark \end{aligned}\)    		  
    الخطوة 7. أجب على السؤال. يجب على كارسون خلط 16 رطلاً من المكسرات مع
    4 أرطال من رقائق الشوكولاتة لإنشاء المزيج السريع.
    التمارين\(\PageIndex{8}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    تريد غريتا صنع 5 أرطال من مزيج الجوز باستخدام الفول السوداني والكاجو. تتطلب ميزانيتها أن يكلفها الخليط 6 دولارات للرطل. تبلغ تكلفة الفول السوداني 4 دولارات للرطل والكاجو 9 دولارات للرطل. كم رطل من الفول السوداني وكم رطل من الكاجو يجب أن تستخدمه؟

    إجابة

    يجب أن تستخدم غريتا 3 أرطال من الفول السوداني و 2 رطل من الكاجو.

    التمارين\(\PageIndex{9}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    يحتوي سامي على معظم المكونات التي يحتاجها لصنع مجموعة كبيرة من الفلفل الحار. العناصر الوحيدة التي يفتقر إليها هي الفاصوليا ولحم البقر المفروم. يحتاج إلى ما مجموعه 20 رطلاً من الفاصوليا ولحم البقر المفروم ولديه ميزانية قدرها 3 دولارات للرطل. سعر الفاصوليا هو 1 دولار للرطل وسعر اللحم المفروم هو 5 دولارات للرطل. كم رطل من الفاصوليا وكم رطل من اللحم المفروم يجب أن يشتريه؟

    إجابة

    يجب على سامي شراء 10 أرطال من الفاصوليا و 10 أرطال من اللحم المفروم.

    تطبيق آخر لمشاكل الخليط يتعلق بإمدادات التنظيف المركزة والمواد الكيميائية الأخرى والمشروبات المختلطة. يتم إعطاء التركيز كنسبة مئوية. على سبيل المثال، منظف منزلي مركّز بنسبة 20٪ يعني أن 20٪ من الكمية الإجمالية عبارة عن منظف، والباقي عبارة عن ماء. للحصول على 35 أونصة من تركيز 20٪، يمكنك مزج 7 أونصات (20٪ من 35) من المنظف مع 28 أونصة من الماء.

    بالنسبة لهذه الأنواع من مشاكل الخليط، سنستخدم النسبة المئوية بدلاً من القيمة لأحد الأعمدة في جدولنا.

    التمارين\(\PageIndex{10}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    ساشينا هي مساعدة مختبر في كلية المجتمع الخاصة بها. إنها تحتاج إلى صنع 200 مليلتر من محلول حمض الكبريتيك بنسبة 40٪ لتجربة معملية. يحتوي المختبر على 25٪ و 50٪ فقط من الحلول في المخزن. كم يجب أن تخلط بين حلول 25٪ و 50٪ لصنع حل 40٪؟

    إجابة
    الخطوة 1. اقرأ المشكلة. قد يساعدنا الشكل في تصور الموقف، ثم
    سننشئ جدولًا لتنظيم المعلومات.
    يجب على Sasheena مزج بعض
    محلول 25٪ وبعض محلول 50٪
    معًا للحصول على 200 مل من محلول 40٪.    		 .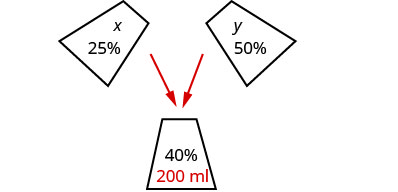
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن مقدار كل حل
    تحتاجه.
    الخطوة 3. اذكر ما نبحث عنه. Let x = عدد مل محلول 25٪.
    y = عدد مل محلول 50٪
    سيساعدنا الجدول في تنظيم البيانات.

    ستقوم بخلط x ml من 25٪ مع y ml من
    50٪ للحصول على 200 مل من محلول 40٪.

    نكتب النسب المئوية كأرقام عشرية في
    الرسم البياني.

    نضرب عدد الوحدات مضروبًا
    في التركيز للحصول على إجمالي
    كمية حمض الكبريتيك في كل محلول.    		 .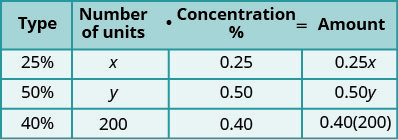
    الخطوة 4. ترجم إلى نظام من
    المعادلات. نحصل على المعادلات
    من عمود الأرقام
    وعمود المبلغ.    		  
    الآن لدينا النظام. .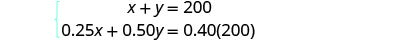
    الخطوة 5. حل نظام المعادلات.
    سنحل النظام عن طريق الإزالة.
    اضرب المعادلة الأولى في −0.5
    لإزالة y.    		 .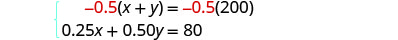
    قم بالتبسيط والإضافة لحل لـ x. .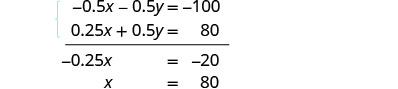
    لحل y، استبدل x = 80 في المعادلة
    الأولى.    		 .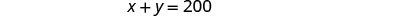
      .
      .
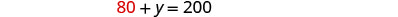
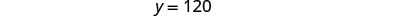
    الخطوة 6. تحقق من الإجابة في المشكلة.

    \(\begin{array}{rll} 80+120 &=&120 \checkmark\\ 0.25(80)+0.50(120) &=&80 \checkmark \\ &&\text{Yes!} \end{array}\)    		  
    الخطوة 7. أجب على السؤال. يجب أن تخلط Sasheena 80 مل من محلول 25٪
    مع 120 مل من محلول 50٪ للحصول على 200 مل
    من محلول 40٪.
    التمارين\(\PageIndex{11}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    يحتاج LeBron إلى 150 مليلترًا من محلول حمض الكبريتيك بنسبة 30٪ لإجراء تجربة معملية ولكن يمكنه فقط الوصول إلى محلول 25٪ و 50٪. ما مقدار الـ 25٪ وكم من محلول الـ 50٪ الذي يجب أن يخلطه لصنع الحل بنسبة 30٪؟

    إجابة

    يحتاج LeBron إلى 120 مل من محلول 25٪ و 30 مل من محلول 50٪.

    التمارين\(\PageIndex{12}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    يحتاج أناتول إلى صنع 250 مليلترًا من محلول حمض الهيدروكلوريك بنسبة 25٪ لإجراء تجربة معملية. يحتوي المختبر على حل بنسبة 10٪ فقط وحل 40٪ في المخزن. ما مقدار الـ 10٪ وكم من حلول الـ 40٪ التي يجب أن يخلطها لصنع الحل بنسبة 25٪؟

    إجابة

    يجب أن يخلط أناتول 125 مل من محلول 10٪ و 125 مل من محلول 40٪.

    حل تطبيقات الاهتمام

    صيغة نماذج التطبيقات ذات الاهتمام هي I = Prt. الفائدة، I، هي نتاج الأصل، P، السعر، r، والوقت، t. في عملنا هنا، سنحسب الفائدة المكتسبة في عام واحد، لذلك ستكون 1.

    نقوم بتعديل عناوين الأعمدة في جدول المزج لإظهار الصيغة المثيرة للاهتمام، كما سترى في التمرين\(\PageIndex{13}\).

    التمارين\(\PageIndex{13}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    لدى عدنان 40 ألف دولار للاستثمار ويأمل في كسب فائدة 7.1٪ سنويًا. سيضع بعض الأموال في صندوق أسهم يكسب 8٪ سنويًا والباقي في سندات تكسب 3٪ سنويًا. كم من المال يجب أن يودعه في كل صندوق؟

    إجابة
    2000 دولار في الأسهم و 7,200 دولار في السندات». >
    الخطوة 1. اقرأ المشكلة. سيساعدنا المخطط على تنظيم المعلومات.
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن المبلغ للاستثمار في كل صندوق.
    الخطوة 3. اذكر ما نبحث عنه. دعونا = المبلغ المستثمر في الأسهم.
    b = المبلغ المستثمر في السندات.
    اكتب سعر الفائدة في صورة عدد عشري
    لكل صندوق.
    اضرب
    : الأصل · السعر · حان الوقت
    للحصول على الفائدة.    		 .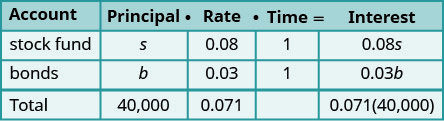
    الخطوة 4. ترجم إلى نظام من
    المعادلات.
    نحصل على نظام المعادلات الخاص بنا من
    العمود الرئيسي وعمود
    الاهتمام.    		 .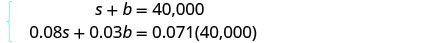
    الخطوة 5. حل نظام المعادلات:
    حل بالحذف.
    اضرب المعادلة العليا في −0.03.    		 .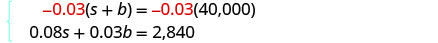
    قم بالتبسيط والإضافة لحل المشكلة من أجل s. .
      .
    لإيجاد b، استبدل s = 32,800 في المعادلة الأولى. .
    .
      .
    الخطوة 6. تحقق من الإجابة في المشكلة. نترك الشيك لك.
    الخطوة 7. أجب على السؤال. يجب أن يستثمر عدنان 32,800 دولار في الأسهم و
    7,200 دولار في السندات.
    هل لاحظت أن العمود الرئيسي يمثل المبلغ الإجمالي للأموال المستثمرة بينما يمثل عمود الفائدة الفائدة المكتسبة فقط؟ وبالمثل، فإن المعادلة الأولى في نظامنا، s + b = 40000، تمثل المبلغ الإجمالي للأموال المستثمرة وتمثل المعادلة الثانية، 0.08 s + 0.03 b = 0.071 (40000)، الفائدة المكتسبة.
    التمارين\(\PageIndex{14}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    كان لدى ليون 50,000 دولار للاستثمار ويأمل في كسب فائدة بنسبة 6.2٪ سنويًا. سيضع بعض الأموال في صندوق أسهم يكسب 7٪ سنويًا والباقي في حساب توفير يكسب 2٪ سنويًا. كم من المال يجب أن يودعه في كل صندوق؟

    إجابة

    يجب أن يضع ليون 42,000 دولار في صندوق الأسهم و 8000 دولار في حساب التوفير.

    التمارين\(\PageIndex{15}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    استثمر جوليوس 7000 دولار في استثمارين في الأسهم. دفع أحد الأسهم فائدة بنسبة 11٪ ودفع السهم الآخر فائدة بنسبة 13٪. حصل على فائدة بنسبة 12.5٪ على إجمالي الاستثمار. كم من المال وضع في كل سهم؟

    إجابة

    استثمر جوليوس 1,750 دولارًا بنسبة 11٪ و 5250 دولارًا بنسبة 13٪.

    التمارين\(\PageIndex{16}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    تدين روزي بمبلغ 21,540 دولارًا على قرضي الطلاب. سعر الفائدة على قرضها المصرفي هو 10.5٪ وسعر الفائدة على القرض الفيدرالي هو 5.9٪. بلغ إجمالي مبلغ الفائدة الذي دفعته العام الماضي 1,669.68 دولارًا. ما هو أصل كل قرض؟

    إجابة
    الخطوة 1. اقرأ المشكلة. سيساعدنا المخطط على تنظيم المعلومات.
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن أصل كل قرض.
    الخطوة 3. اذكر ما نبحث عنه. Let b = أصل القرض المصرفي.
    f = رأس المال على القرض الفيدرالي
    يبلغ إجمالي القروض 21,540 دولارًا.  
    سجل أسعار الفائدة كأرقام عشرية
    في الرسم البياني.    		 .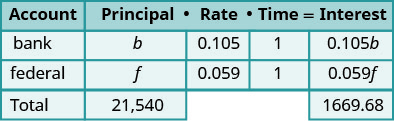
    اضرب باستخدام الصيغة l = Pr t
    للحصول على الفائدة.    		  
    الخطوة 4. ترجم إلى نظام من
    المعادلات.
    يأتي نظام المعادلات من
    العمود الرئيسي
    وعمود الاهتمام.    		 .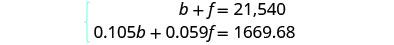
    الخطوة 5. حل نظام المعادلات
    سنستخدم الاستبدال لحلها.
    حل المعادلة الأولى لـ b.    		 .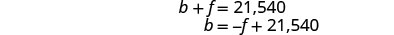
    استبدل ب = − f + 21,540 في المعادلة
    الثانية.    		 .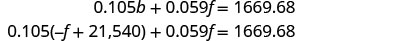
    قم بالتبسيط والحل لـ f. .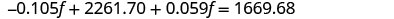
      .
      .
      .
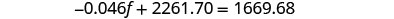
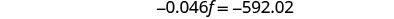
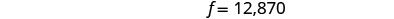
    لإيجاد b، استبدل f = 12,870
    بالمعادلة الأولى.    		 .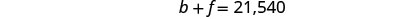
    .
      .
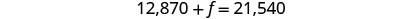
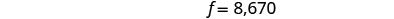
    الخطوة 6. تحقق من الإجابة في
    المشكلة.    		 نترك الشيك لك.
    الخطوة 7. أجب على السؤال. أصل القرض المصرفي هو 12,870 دولارًا
    وأصل القرض الفيدرالي هو 8,670 دولارًا.
    التمارين\(\PageIndex{17}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    تدين لورا بمبلغ 18,000 دولار على قروض طلابها. سعر الفائدة على القرض المصرفي هو 2.5٪ وسعر الفائدة على القرض الفيدرالي هو 6.9٪. بلغ إجمالي مبلغ الفائدة الذي دفعته العام الماضي 1,066 دولارًا. ما هو أصل كل قرض؟

    إجابة

    وكان المبلغ الرئيسي للقرض المصرفي 4000 دولار. كان المبلغ الرئيسي للقرض الفيدرالي 14000 دولار.

    التمارين\(\PageIndex{18}\)

    ترجم إلى نظام المعادلات وقم بحلها:

    تدين شركة Jill's Sandwich Shoppe بمبلغ 65200 دولار على قرضين تجاريين، أحدهما بفائدة 4.5٪ والآخر بفائدة 7.2٪. بلغ إجمالي مبلغ الفائدة المستحقة العام الماضي 3,582 دولارًا. ما هو أصل كل قرض؟

    إجابة

    كان المبلغ الأساسي لـ 41,200 دولار بنسبة 4.5%. كان المبلغ الأساسي 24,000 دولار بنسبة 7.2%.

    ملاحظة

    يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل مشكلات التطبيق باستخدام أنظمة المعادلات الخطية.

    المفاهيم الرئيسية

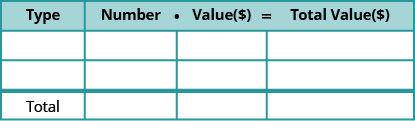
    • جدول لتطبيقات العملات والمزيج
      هذا الجدول فارغ في الغالب. يحتوي على أربعة أعمدة وأربعة صفوف. يُطلق على الصف الأخير اسم «الإجمالي». يسمي الصف الأول كل عمود باسم «النوع» و «الرقم في القيمة = القيمة الإجمالية».
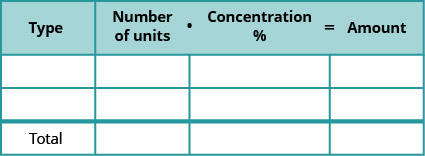
    • جدول لتطبيقات التركيز
      هذا الجدول فارغ في الغالب. يحتوي على أربعة أعمدة وأربعة صفوف. يُطلق على الصف الأخير اسم «الإجمالي». يسمي الصف الأول كل عمود باسم «النوع» و «عدد الوحدات مضروبًا في التركيز = الكمية».
    • جدول لتطبيقات الفائدة
      هذا الجدول فارغ في الغالب. يحتوي على خمسة أعمدة وأربعة صفوف. يُطلق على الصف الأخير اسم «الإجمالي». يسمي الصف الأول كل عمود باسم «النوع» و «الأوقات الرئيسية مرات السعر الوقت = الفائدة»