4.5: استخدم صورة المنحدر والجزء المقطوع لمعادلة الخط المستقيم
- Page ID
- 200254
في نهاية هذا القسم، ستكون قادرًا على:
- تعرف على العلاقة بين الرسم البياني وشكل المنحدر - المقطوع لمعادلة الخط المستقيم
- حدد شكل المنحدر والجزء الصادي لمعادلة الخط المستقيم
- ارسم خطًا بيانيًا باستخدام المنحدر والفاصل
- اختر الطريقة الأكثر ملاءمة لرسم خط
- رسم تطبيقات المنحدر-التقاطع وتفسيرها
- استخدم المنحدرات لتحديد الخطوط المتوازية
- استخدم المنحدرات لتحديد الخطوط العمودية
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- إضافة:\(\frac{x}{4} + \frac{1}{4}\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.7.1. - أوجد قيمة المعاملة بالمثل لـ\(\frac{3}{7}\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.6.19. - حل\(2x−3y=12\) لـ\(y\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.6.16.
تعرف على العلاقة بين الرسم البياني وصيغة المنحدر والجزء المقطوع لمعادلة الخط المستقيم
لقد قمنا برسم المعادلات الخطية من خلال رسم النقاط، واستخدام القطع المقطوعة، والتعرف على الخطوط الأفقية والعمودية، واستخدام طريقة النقط-المنحدر. بمجرد أن نرى كيفية ارتباط المعادلة في شكل المنحدر - التقاطع والرسم البياني الخاص بها، سيكون لدينا طريقة أخرى يمكننا استخدامها لرسم الخطوط.
في التمثيل البياني للمعادلات الخطية في متغيرين، رسمنا خط المعادلة\(y=12x+3\) برسم النقاط. انظر الشكل\(\PageIndex{1}\). دعونا نجد منحدر هذا الخط.
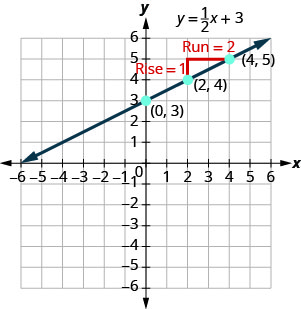
تظهر لنا الخطوط الحمراء الارتفاع\(1\) والركض\(2\). الاستبدال في صيغة المنحدر:
\[\begin{aligned} m &=\frac{\text { rise }}{\text { rise }} \\ m &=\frac{1}{2} \end{aligned}\]
ما الجزء\(y\) المقطوع من الخط؟ \(y\)التقاطع -هو المكان الذي يعبر فيه الخط\(y\) المحور، لذا فإن\(y\) -Intercept هو المكان الذي يعبر فيه الخط\((0,3)\). معادلة هذا الخط هي:
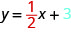
لاحظ أن الخط يحتوي على:

عندما يتم حل المعادلة الخطية\(y\)، يكون معامل\(x\) المصطلح -هو المنحدر والحد الثابت هو\(y\) الإحداثي\(y\) -التقاطع. نقول أن المعادلة\(y=\frac{1}{2}x+3\) في شكل منحدر - مقطع.
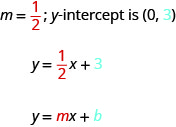
شكل المنحدر - المقطوع لمعادلة خط مستقيم بمنحدر مم\(y\) وقطعه -\((0,b)\) يساوي،
\[y=mx+b\]
في بعض الأحيان يُطلق على نموذج المنحدر - التقاطع اسم «y -form».
استخدم الرسم البياني للعثور على ميل الخط وقطعه،\(y=2x+1\).\(y\)
قارن هذه القيم بالمعادلة\(y=mx+b\).
- إجابة
-
للعثور على منحدر الخط، نحتاج إلى اختيار نقطتين على الخط. سنستخدم النقاط\((0,1)\) و\((1,3)\).
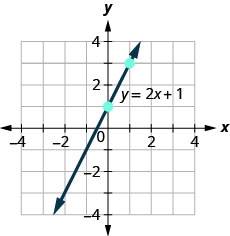
ابحث عن الصعود والجري. 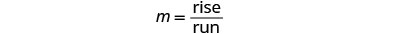
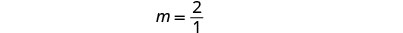
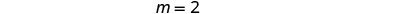
ابحث عن\(y\) التقاطع -للخط. \(y\)الاعتراض -هو النقطة\((0, 1)\). 
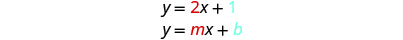
المنحدر هو نفس المعامل\(x\)\(y\) والإحداثيات\(y\) -Intercept هي نفس الحد الثابت.
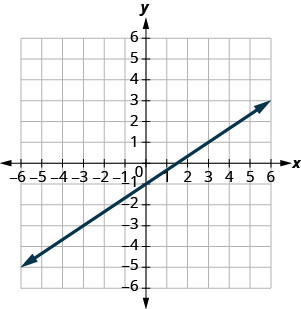
استخدم الرسم البياني للعثور على\(y\) ميل الخط وقطعه\(y=\frac{2}{3}x−1\). قارن هذه القيم بالمعادلة\(y=mx+b\).
- إجابة
-
المنحدر\(m = \frac{2}{3}\)\(y\) والاعتراض\((0,−1)\)
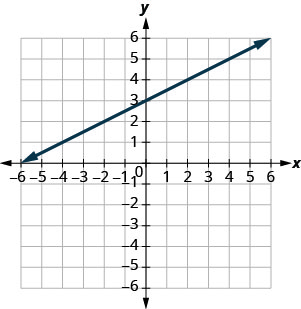
استخدم الرسم البياني للعثور على\(y\) ميل الخط وقطعه\(y=\frac{1}{2}x+3\). قارن هذه القيم بالمعادلة\(y=mx+b\).
- إجابة
-
المنحدر\(m = \frac{1}{2}\)\(y\) والاعتراض\((0,3)\)
حدِّد المنحدر\(y\) والجزء المقطوع من معادلة الخط المستقيم
في فهم[1] ميل الخط المستقيم، رسمنا خطًا بيانيًا باستخدام المنحدر والنقطة. عندما نحصل على معادلة في صورة المنحدر-التقاطع، يمكننا استخدام\(y\) التقاطع -كنقطة، ثم عد المنحدر من هناك. دعونا نتدرب على إيجاد قيم المنحدر\(y\) والجزء المقطوع من معادلة الخط المستقيم.
حدِّد ميل الخط\(y\) المستقيم والجزء المقطوع منه باستخدام المعادلة\(y=−3x+5\).
- إجابة
-
نحن نقارن معادلتنا بصيغة المنحدر والمقطع للمعادلة.
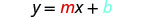
اكتب معادلة الخط المستقيم. 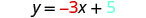
حدد المنحدر. 
التعرف\(y\) على التقاطع. 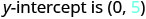
حدد منحدر الخط\(y\) والجزء المقطوع منه\(y=\frac{2}{5}x−1\).
- إجابة
-
\(\frac{2}{5}\)؛ (0، −1)
حدد منحدر الخط\(y\) والجزء المقطوع منه\(y=−\frac{4}{3}x+1\).
- إجابة
-
\(-\frac{4}{3}\)؛ (0,1)
عندما لا تُعطى معادلة الخط المستقيم في شكل منحدر — مقطع، ستكون خطوتنا الأولى هي حل المعادلة الخاصة بـ\(y\).
حدِّد ميل الخط\(y\) المستقيم والجزء المقطوع منه باستخدام المعادلة\(x+2y=6\).
- إجابة
-
هذه المعادلة ليست في شكل منحدر أو مقطع. لمقارنتها بنموذج المنحدر - التقاطع، يجب علينا أولاً حل المعادلة الخاصة بـ\(y\).
حل لـ\(y\). \(x+2y=6\) اطرح x من كل جانب. 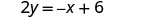
قسّم كلا الجانبين على\(2\). 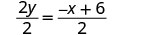
قم بالتبسيط. 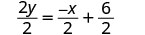
(تذكر:\(\frac{a+b}{c} = \frac{a}{c} + \frac{b}{c}\)) قم بالتبسيط. 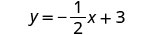
اكتب شكل المنحدر والجزء المقطوع لمعادلة الخط المستقيم. 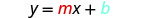
اكتب معادلة الخط المستقيم. 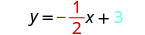
حدد المنحدر. 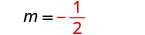
التعرف\(y\) على التقاطع. 
حدد منحدر الخط\(y\) والجزء المقطوع منه\(x+4y=8\).
- إجابة
-
\(-\frac{1}{4}\)؛ (0,2)
حدد منحدر الخط\(y\) والجزء المقطوع منه\(3x+2y=12\).
- إجابة
-
\(-\frac{2}{3}\)؛ (0,6)
رسم خط مستقيم باستخدام ميله والجزء المقطوع منه
الآن بعد أن عرفنا كيفية إيجاد ميل الخط\(y\) والجزء المقطوع منه من معادلته، يمكننا رسم الخط برسم\(y\) التقاطع -ثم استخدام المنحدر للعثور على نقطة أخرى.
ارسم خط المعادلة بيانيًا\(y=4x−2\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-


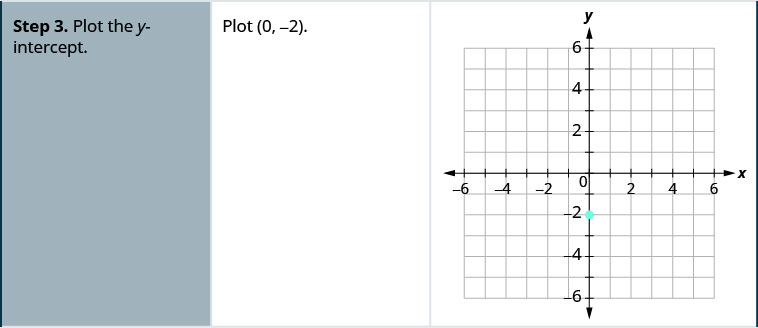

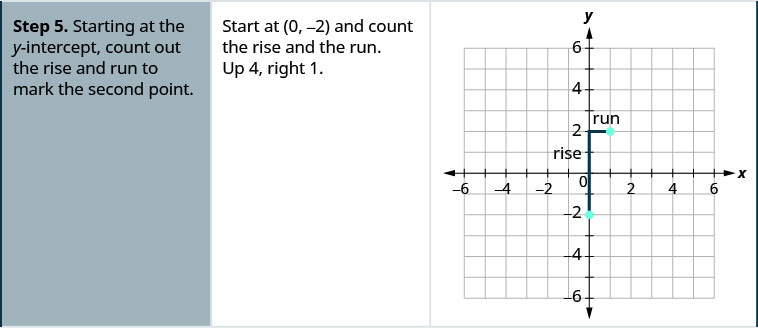
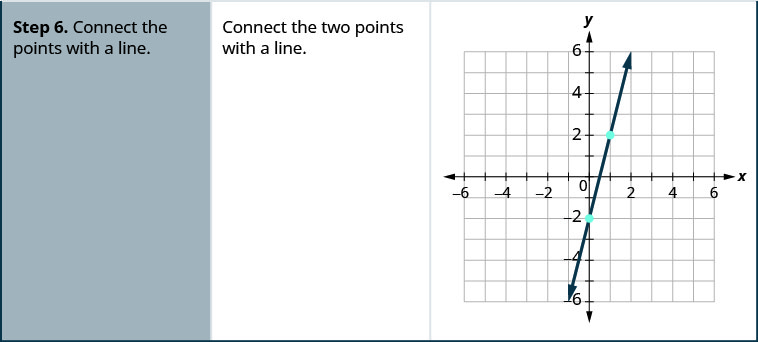
ارسم خط المعادلة بيانيًا\(y=4x+1\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
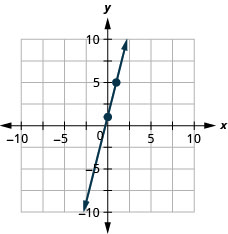
ارسم خط المعادلة بيانيًا\(y=2x−3\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
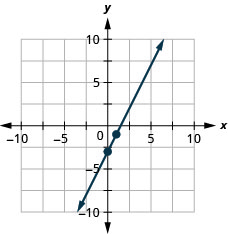
- أوجد شكل التقاطع المنحدر لمعادلة الخط المستقيم.
- حدد المنحدر وقم\(y\) بالتقاطع.
- ارسم\(y\) نقطة التقاطع.
- استخدم صيغة المنحدر\(\frac{\text{rise}}{\text{run}}\) لتحديد الارتفاع والجري.
- بدءًا من\(y\) نقطة التقاطع، قم بحساب الارتفاع والجري لتحديد النقطة الثانية.
- قم بتوصيل النقاط بخط.
ارسم خط المعادلة بيانيًا\(y=−x+4\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
دقق.\(y=mx+b\) توجد المعادلة في صورة منحدر-مقطع. \(y=−x+4\) حدد المنحدر وقم\(y\) بالتقاطع. \(m=−1\) \(y\)-إنترسيبت هو\((0, 4)\) ارسم\(y\) نقطة التقاطع. انظر الرسم البياني أدناه. حدد الارتفاع والجري. \(m = \frac{-1}{1}\) احسب الارتفاع وركض لتحديد النقطة الثانية. انهض\(−1\)، اركض\(1\) ارسم الخط. 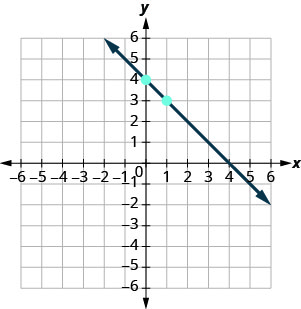
للتحقق من عملك، يمكنك العثور على نقطة أخرى على الخط والتأكد من أنها حل للمعادلة. في الرسم البياني نرى الخط يمر\((4, 0)\). - \(\begin{array}{l}{y=-x+4} \\ {0\stackrel{?}{=}-4+4} \\ {0=0\checkmark}\end{array}\)
ارسم خط المعادلة بيانيًا\(y=−x−3\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
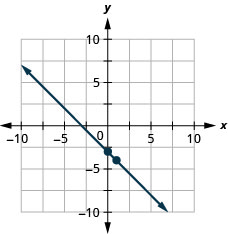
ارسم خط المعادلة بيانيًا\(y=−x−1\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
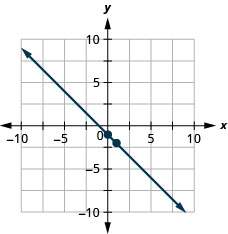
ارسم خط المعادلة بيانيًا\(y=−\frac{2}{3}x−3\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
\(y=mx+b\) توجد المعادلة في صورة منحدر-مقطع. \(y=−\frac{2}{3}x−3\) حدد المنحدر وقم\(y\) بالتقاطع. \(m = -\frac{2}{3}\)؛\(y\) - الاعتراض هو\((0, −3)\) ارسم\(y\) نقطة التقاطع. انظر الرسم البياني أدناه. حدد الارتفاع والجري. احسب الارتفاع وركض لتحديد النقطة الثانية. ارسم الخط. 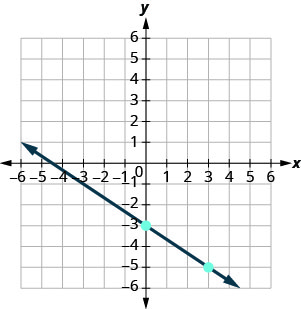
ارسم خط المعادلة بيانيًا\(y=−\frac{5}{2}x+1\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
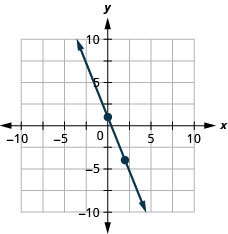
ارسم خط المعادلة بيانيًا\(y=−\frac{3}{4}x−2\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
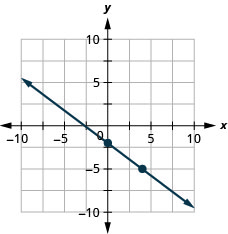
ارسم خط المعادلة بيانيًا\(4x−3y=12\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
\(4x−3y=12\) أوجد شكل المنحدر-التقاطع للمعادلة. \(−3y=−4x+12\) \(−\frac{3y}{3}=\frac{−4x+12}{−3}\) المعادلة الآن في شكل منحدر - مقطع. \(y=\frac{4}{3}x−4\) حدد المنحدر وقم\(y\) بالتقاطع. \(m=\frac{4}{3}\) \(y\)-الاعتراض هو\((0, −4)\) ارسم\(y\) نقطة التقاطع. انظر الرسم البياني أدناه. حدد الارتفاع والجري؛ احسب الارتفاع والجري لتحديد النقطة الثانية. ارسم الخط. 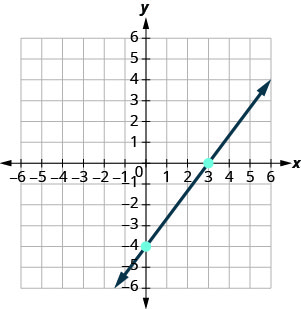
ارسم خط المعادلة بيانيًا\(2x−y=6\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
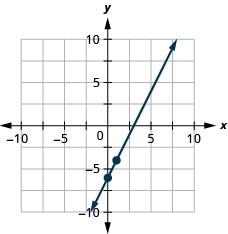
ارسم خط المعادلة بيانيًا\(3x−2y=8\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
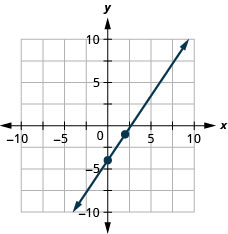
لقد استخدمنا شبكة تحتوي على جميع المعادلات التي قمنا\(x\) بتمثيلها بيانيًا حتى الآن وكل\(y\) منهما ينتقل من تقريبًا\(−10\) إلى\(10\) آخر. لا يمكن رسم جميع المعادلات الخطية على هذه الشبكة الصغيرة. في كثير من الأحيان، خاصة في التطبيقات التي تحتوي على بيانات واقعية، سنحتاج إلى توسيع المحاور إلى أرقام إيجابية أكبر أو أرقام سالبة أصغر.
ارسم خط المعادلة بيانيًا\(y=0.2x+45\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
سنستخدم شبكة مع انتقال المحاور من حوالي\(−80\) إلى\(80\).
\(y=mx+b\) توجد المعادلة في صورة منحدر-مقطع. \(y=0.2x+45\) حدد المنحدر وقم\(y\) بالتقاطع. \(m=0.2\) \(y\)الاعتراض الإلكتروني هو\((0, 45)\) ارسم\(y\) نقطة التقاطع. انظر الرسم البياني أدناه. احسب الارتفاع وركض لتحديد النقطة الثانية. المنحدر هو\(m=0.2\)؛ في شكل كسور وهذا يعني\(m=\frac{2}{10}\). بالنظر إلى مقياس الرسم البياني الخاص بنا، سيكون من الأسهل استخدام الكسر المكافئ\(m=\frac{10}{50}\). ارسم الخط. 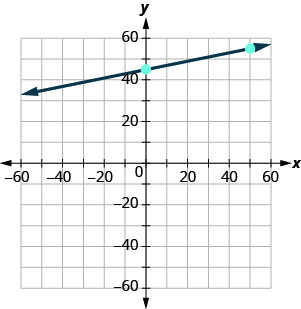
ارسم خط المعادلة بيانيًا\(y=0.5x+25\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
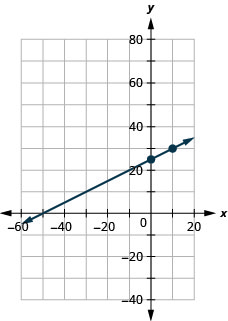
ارسم خط المعادلة بيانيًا\(y=0.1x−30\) باستخدام المنحدر والجزء\(y\) المقطوع.
- إجابة
-
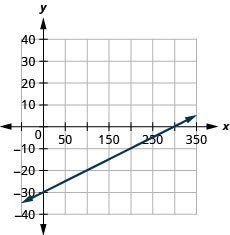
الآن بعد أن قمنا برسم الخطوط باستخدام المنحدر والجزء\(y\) المقطوع، دعونا نلخص جميع الطرق التي استخدمناها لرسم الخطوط. انظر الشكل\(\PageIndex{2}\).

اختر الطريقة الأكثر ملاءمة لرسم خط
الآن بعد أن رأينا عدة طرق يمكننا استخدامها لرسم الخطوط، كيف نعرف الطريقة التي يجب استخدامها لمعادلة معينة؟
بينما يمكننا رسم النقاط، أو استخدام نموذج التقاطع المنحدر، أو العثور على الأجزاء المقطوعة لأي معادلة، إذا تعرفنا على الطريقة الأكثر ملاءمة لرسم نوع معين من المعادلات، فإن عملنا سيكون أسهل. بشكل عام، لا يعد رسم النقاط الطريقة الأكثر فعالية لرسم خط. لقد رأينا طرقًا أفضل في الأقسام 4.3 و 4.4 وما قبلها في هذا القسم. لنبحث عن بعض الأنماط للمساعدة في تحديد الطريقة الأكثر ملاءمة لرسم خط.
فيما يلي ست معادلات قمنا بتمثيلها بيانيًا في هذا الفصل، والطريقة التي استخدمناها لرسم كل منها بيانيًا.
\[\begin{array}{lll}{\text{#1}}&{\text {Equation }} & {\text { Method }} \\ {\text{#2}}&{x=2} & {\text { Vertical line }} \\ {\text{#3}}&{y=4} & {\text { Hortical line }} \\ {\text{#4}}&{-x+2 y=6} & {\text { Intercepts }} \\ {\text{#5}}&{4 x-3 y=12} & {\text { Intercepts }} \\ {\text{#6}}&{y=4 x-2} & {\text { Slope-intercept }} \\{\text{#7}}& {y=-x+4} & {\text { Slope-intercept }}\end{array}\]
تحتوي كل من المعادلات #1 و #2 على متغير واحد فقط. تذكر أن قيمة المتغير الواحد ثابتة في معادلات بهذا الشكل؛ ولا تعتمد على قيمة المتغير الآخر. تحتوي معادلات هذا النموذج على رسوم بيانية عبارة عن خطوط رأسية أو أفقية.
في المعادلتين #3\(x\) و #4،\(y\) كلاهما على نفس الجانب من المعادلة. هاتان المعادلتان من الشكل\(Ax+By=C\). قمنا باستبدال\(y=0\) البحث عن\(x\) -incircept والعثور\(x=0\) على\(y\) -Intercept، ثم وجدنا نقطة ثالثة باختيار قيمة أخرى لـ\(x\) أو\(y\).
تتم كتابة المعادلتين #5 و #6 في شكل منحدر-متقاطع. بعد تحديد المنحدر والجزء\(y\) المقطوع من المعادلة، استخدمناهما لرسم الخط.
هذا يؤدي إلى الاستراتيجية التالية.
ضع في اعتبارك شكل المعادلة.
- إذا كان يحتوي على متغير واحد فقط، فهو خط عمودي أو أفقي.
- \(x=a\)هو خط عمودي يمر عبر\(x\) المحور -at\(a\).
- \(y=b\)هو خط أفقي يمر عبر\(y\) المحور -at\(b\).
- إذا\(y\) تم عزله على أحد طرفي المعادلة، في النموذج\(y=mx+b\)، قم بالرسم البياني باستخدام المنحدر\(y\) والجزء المقطوع.
- حدد المنحدر والجزء\(y\) المقطوع ثم قم بالرسم البياني.
- إذا كانت المعادلة من النموذج\(Ax+By=C\)، فأوجد القطع المقطوعة.
- ابحث عن\(y\) نقاط التقاطع\(x\) - و -، والنقطة الثالثة، ثم الرسم البياني.
حدد الطريقة الأكثر ملاءمة لرسم كل سطر.
- \(y=−6\)
- \(5x−3y=15\)
- \(x=7\)
- \(y=\frac{2}{5}x−1\).
- إجابة
-
1. \(y=−6\)
تحتوي هذه المعادلة على متغير واحد فقط،\(y\). الرسم البياني الخاص به هو خط أفقي يعبر\(y\) المحور -at\(−6\).2. \(5x−3y=15\)
هذه المعادلة من النموذج\(Ax+By=C\). أسهل طريقة للرسم البياني هي العثور على نقاط الاعتراض ونقطة أخرى.3. \(x=7\)
هناك متغير واحد فقط،\(x\). الرسم البياني عبارة عن خط عمودي يعبر\(x\) المحور -عند\(7\).4. \(y=\frac{2}{5}x−1\)
نظرًا لأن هذه المعادلة في\(y=mx+b\) الشكل، سيكون من الأسهل رسم هذا الخط بيانيًا باستخدام المنحدر\(y\) والجزء المقطوع.
حدد الطريقة الأكثر ملاءمة لرسم كل سطر:
- \(3x+2y=12\)
- \(y=4\)
- \(y=\frac{1}{5}x−4\)
- \(x=−7\)
- إجابة
-
- عمليات الاعتراض
- خط أفقي
- اعتراض المنحدر
- خط عمودي
حدد الطريقة الأكثر ملاءمة لرسم كل سطر:
- \(x=6\)
- \(y=−\frac{3}{4}x+1\)
- \(y=−8\)
- \(4x−3y=−1\)
- إجابة
-
- خط عمودي
- اعتراض المنحدر
- خط أفقي
- عمليات الاعتراض
رسم بياني وتفسير تطبيقات المنحدر — التقاطع
تم تصميم العديد من تطبيقات العالم الحقيقي من خلال المعادلات الخطية. سنلقي نظرة على بعض التطبيقات هنا حتى تتمكن من رؤية كيفية ارتباط المعادلات المكتوبة في شكل المنحدر - التقاطع بمواقف العالم الحقيقي.
عادةً عندما تمثل المعادلة الخطية موقفًا حقيقيًا، يتم استخدام أحرف مختلفة للمتغيرات، بدلاً من\(x\) و\(y\). تذكرنا أسماء المتغيرات بالكميات التي يتم قياسها.
تستخدم\(F=\frac{9}{5}C+32\) المعادلة لتحويل درجات الحرارة\(C\)، على مقياس السيلزيوس إلى درجات حرارة\(F\)، على مقياس فهرنهايت.
- أوجد درجة حرارة فهرنهايت لدرجة حرارة مئوية قدرها\(0\).
- أوجد درجة حرارة فهرنهايت لدرجة حرارة مئوية قدرها\(20\).
- قم بتفسير المنحدر\(F\) والجزء المقطوع للمعادلة.
- رسم المعادلة بيانيًا.
- إجابة
-
1. \(\begin{array}{ll}{\text { Find the Fahrenheit temperature for a Celsius temperature of } 0 .} & {F=\frac{9}{5} C+32} \\ {\text { Find } F \text { when } C=0 .} & {F=\frac{9}{5}(0)+32} \\ {\text { Simplify. }} & {F=32}\end{array}\)
2. \ ابدأ {array} {ll} {\ text {ابحث عن درجة حرارة فهرنهايت لدرجة حرارة مئوية تبلغ} 20.} & {F=\ frac {9} {5} C+32}\\\ النص {البحث} F\ النص {عندما} C=20.} & {F=\ frac {9} {5} (20) +32}\\\ النص {التبسيط.}} & {F=36+32}\\\\ النص {التبسيط}} و {F=68}\ النهاية {المصفوفة}
3. قم بتفسير المنحدر\(F\) والجزء المقطوع للمعادلة.
على الرغم من أن هذه المعادلة تستخدم\(F\)\(C\) الرمال، إلا أنها لا تزال في شكل منحدر - تقاطع.
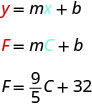
المنحدر،\(\frac{9}{5}\)، يعني أن درجة الحرارة فهرنهايت (\(F\)) تزداد\(9\) بالدرجات عندما تزيد درجة الحرارة المئوية (\(C\))\(5\) بالدرجات.
يعني التقاطع\(F\) -Intercept أنه عندما تكون درجة الحرارة\(0°\) على مقياس السيلزيوس، فإنها تكون\(32°\) على مقياس فهرنهايت.
4. رسم المعادلة بيانيًا.
سنحتاج إلى استخدام مقياس أكبر من المعتاد. ابدأ عند\(F\) التقاطع\((0,32)\) -ثم احسب الصعود والجري للحصول\(5\) على نقطة ثانية.\(9\) انظر الشكل\(\PageIndex{3}\).
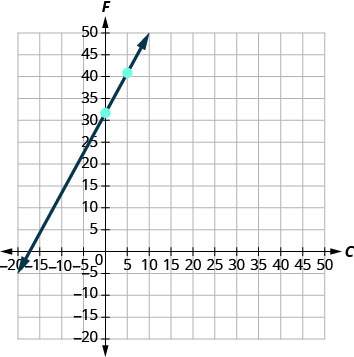
الشكل\(\PageIndex{3}\)
\(h=2s+50\)تُستخدم المعادلة لتقدير ارتفاع المرأة بالبوصة,\(h\), بناءً على حجم حذائها,\(s\).
- قم بتقدير ارتفاع الطفل الذي يرتدي مقاس حذاء نسائي\(0\).
- قم بتقدير ارتفاع المرأة بحجم الحذاء\(8\).
- قم بتفسير المنحدر\(h\) والجزء المقطوع للمعادلة.
- رسم المعادلة بيانيًا.
- إجابة
-
- \(50\)بوصة
- \(66\)بوصة
- المنحدر\(2\)، يعني أن الارتفاع\(h\)، يزداد بمقدار\(2\) البوصة عندما يزداد حجم الحذاء بمقدار\(s\) 1 بوصة\(1\). يعني التقاطع\(h\) -Intercept أنه عندما يكون مقاس الحذاء\(0\)، يكون الارتفاع\(50\) بوصات.
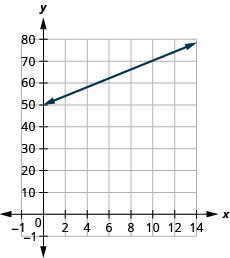
\(T=\frac{1}{4}n+40\)تُستخدم المعادلة لتقدير درجة الحرارة بالدرجات فهرنهايت\(T\)، بناءً على عدد أغاني الكريكت،\(n\)، في دقيقة واحدة.
- قم بتقدير درجة الحرارة عند عدم وجود غردات.
- قم بتقدير درجة الحرارة عندما يكون عدد التغريدات في دقيقة واحدة\(100\).
- قم بتفسير المنحدر\(T\) والجزء المقطوع للمعادلة.
- رسم المعادلة بيانيًا.
- إجابة
-
- \(40\)درجات
- \(65\)درجات
- المنحدر\(\frac{1}{4}\)، يعني أن درجة الحرارة فهرنهايت (\(F\)) تزداد\(1\) درجة عندما يزداد عدد الغردات\(n\)،، بمقدار\(4\). تعني كلمة\(T\) -Intercept أنه عندما يكون عدد التغريدات\(0\)، تكون درجة الحرارة\(40°\).
تتكون تكلفة إدارة بعض أنواع الأعمال من عنصرين - تكلفة ثابتة وتكلفة متغيرة. التكلفة الثابتة هي نفسها دائمًا بغض النظر عن عدد الوحدات المنتجة. هذه هي تكلفة الإيجار والتأمين والمعدات والإعلانات وغيرها من العناصر التي يجب دفعها بانتظام. تعتمد التكلفة المتغيرة على عدد الوحدات المنتجة. إنه مخصص للمواد والعمالة اللازمة لإنتاج كل عنصر.
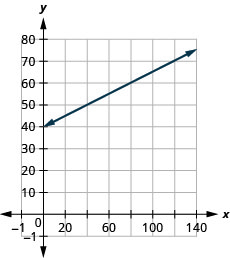
لدى Stella شركة منزلية تبيع البيتزا الذواقة. \(C=4p+25\)تُمثِّل المعادلة العلاقة بين تكلفتها الأسبوعية بالدولار وعدد البيتزا التي تبيعها.\(C\)\(p\)
- ابحث عن تكلفة Stella لمدة أسبوع عندما لا تبيع البيتزا.
- ابحث عن التكلفة لمدة أسبوع عندما تبيع\(15\) البيتزا.
- قم بتفسير المنحدر\(C\) والجزء المقطوع للمعادلة.
- رسم المعادلة بيانيًا.
- إجابة
-
1. ابحث عن تكلفة Stella لمدة أسبوع عندما لا تبيع البيتزا. 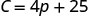
ابحث عن\(C\) متى\(p=0\). 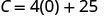
قم بالتبسيط. 
التكلفة الثابتة لستيلا هي\($25\) عندما لا تبيع البيتزا. 2. ابحث عن التكلفة لمدة أسبوع عندما تبيع\(15\) البيتزا. 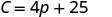
ابحث عن\(C\) متى\(p=15\). 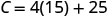
قم بالتبسيط. 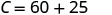

تكاليف ستيلا هي\($85\) عندما تبيع\(15\) البيتزا. 3. قم بتفسير المنحدر\(C\) والجزء المقطوع للمعادلة. 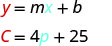
يعني المنحدر أن التكلفة تزداد بمقدار النصف\($4\) لكل بيتزا تبيعها ستيلا.\(4\) يعني\(C\) الاعتراض أنه حتى عندما لا تبيع ستيلا أي بيتزا، فإن تكاليفها لهذا الأسبوع هي\($25\). 4. رسم المعادلة بيانيًا. سنحتاج إلى استخدام مقياس أكبر من المعتاد. ابدأ عند\(C\) التقاطع\((0, 25)\) -ثم احسب الصعود والجري للحصول\(1\) على نقطة ثانية.\(4\) 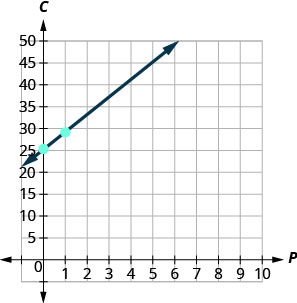
سام يقود شاحنة توصيل. \(C=0.5m+60\)تُمثِّل المعادلة العلاقة بين التكلفة الأسبوعية التي يقطعها\(C\)، بالدولار\(m\)، وعدد الأميال التي يقودها.
- ابحث عن تكلفة سام لمدة أسبوع عندما يقود\(0\) أميالًا.
- ابحث عن التكلفة لمدة أسبوع عندما يقود\(250\) أميالًا.
- قم بتفسير المنحدر\(C\) والجزء المقطوع للمعادلة.
- رسم المعادلة بيانيًا.
- إجابة
-
- \($60\)
- \($185\)
- المنحدر\(0.5\)، يعني أن التكلفة الأسبوعية\(C\)، تزداد\($0.50\) عندما يزداد عدد الأميال\(n\) المقطوعة بمقدار\(1\). تعني النقطة\(C\) -Intercept أنه عندما يكون عدد الأميال المقطوعة\(0\)، تكون التكلفة الأسبوعية هي\($60\).
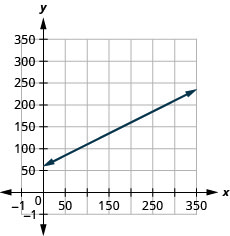
تعمل لورين في مجال الخط. \(C=1.8n+35\)تُمثل المعادلة العلاقة بين تكلفتها الأسبوعية\(C\)، بالدولار وعدد دعوات الزفاف\(n\)، التي تكتبها.
- ابحث عن تكلفة لورين لمدة أسبوع عندما لا تكتب أي دعوات.
- ابحث عن التكلفة لمدة أسبوع عندما تكتب\(75\) الدعوات.
- قم بتفسير المنحدر\(C\) والجزء المقطوع للمعادلة.
- رسم المعادلة بيانيًا.
- إجابة
-
- \($35\)
- \($170\)
- يعني المنحدر أن التكلفة الأسبوعية تزداد\($1.80\) بمقدار زيادة عدد الدعوات بمقدار\(1.80\).\(1.8\)\(C\)\(n\) تعني كلمة\(C\) -incept أنه عندما يكون عدد الدعوات\(0\)، تكون التكلفة الأسبوعية هي\($35\).
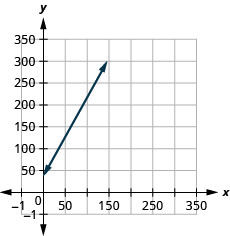
استخدم المنحدرات لتحديد الخطوط المتوازية
يشير ميل الخط إلى مدى انحدار الخط وما إذا كان يرتفع أو ينخفض عندما نقرأه من اليسار إلى اليمين. يُطلق على الخطين اللذين لهما نفس المنحدر الخطوط المتوازية. لا تتقاطع الخطوط المتوازية أبدًا.

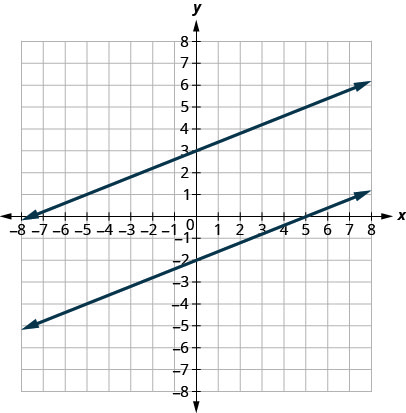
ماذا عن الخطوط العمودية؟ ميل الخط العمودي غير محدد، لذلك لا تتناسب الخطوط الرأسية مع التعريف أعلاه. نقول أن الخطوط العمودية\(x\) ذات التقاطعات المختلفة متوازية. انظر الشكل\(\PageIndex{5}\).
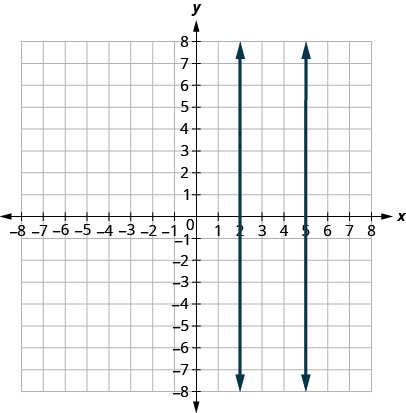
الخطوط المتوازية هي خطوط في نفس المستوى لا تتقاطع.
- تحتوي الخطوط المتوازية على نفس المنحدر\(y\) وحواجز مختلفة.
- إذا كانت منحدرات خطين متوازيين\(m_{1}\) وما\(m_{2}\) زالت كذلك\(m_{1} = m_{2}\).
- تحتوي الخطوط العمودية المتوازية على\(x\) تقاطعات مختلفة.
دعونا نرسم المعادلات\(y=−2x+3\)\(2x+y=−1\) وعلى نفس الشبكة. المعادلة الأولى موجودة بالفعل في شكل منحدر:\(y=−2x+3\). نحل المعادلة الثانية لـ\(y\):
\[\begin{aligned} 2x+y &=-1 \\ y &=-2x-1 \end{aligned}\]
رسم الخطوط بيانيًا.
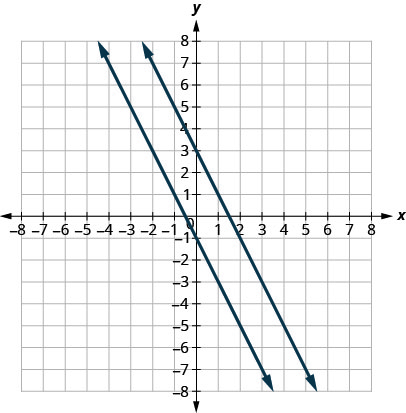
لاحظ أن الخطوط تبدو متوازية. ما ميل كل خط مستقيم؟ ما الجزء\(y\) المقطوع لكل خط؟
\[\begin{array}{lll} {y} & {=m x+b} & {y=m x+b} \\ {y} & {=-2 x+3} & {y=-2 x-1} \\ {m} & {=-2} & {m=-2}\\ {b} & {=3,(0,3)} & {b=-1,(0,-1)}\end{array}\]
منحدرات الخطوط هي نفسها ويختلف\(y\) التقاطع لكل خط. لذلك نحن نعلم أن هذه الخطوط متوازية.
نظرًا لأن الخطوط المتوازية لها نفس المنحدر\(y\) وأجزاء التقاطع المختلفة، يمكننا الآن فقط النظر إلى شكل المنحدر - التقاطع لمعادلات الخطوط وتحديد ما إذا كانت الخطوط متوازية.
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(3x−2y=6\) والخطوط\(y = \frac{3}{2}x + 1\) متوازية.
- إجابة
-
\(\begin{array} {lrll} {\text { Solve the first equation for } y .} &{ 3 x-2 y} &{=} &{6}\\{} & {\frac{-2 y}{-2}} &{ =}&{-3 x+6 }\\ {} &{\frac{-2 y}{-2}}&{ =}&{\frac{-3 x+6}{-2}} \\ {} & {y }&{=}&{\frac{3}{2} x-3} \end{array}\)
المعادلة الآن في شكل منحدر - مقطع.
معادلة الخط الثاني موجودة بالفعل في شكل منحدر.
حدد المنحدر والجزء\(y\) المقطوع لكلا الخطين.
\(\begin{array}{lll}{y=\frac{3}{2} x+1} & {} & {y=\frac{3}{2} x-3} \\ {y=m x+b} & {} & {y=m x+b}\\ {m=\frac{3}{2}} & {} & {m=\frac{3}{2}} \\ {y\text{-intercept is }(0, 1)} & {} & {y\text{-intercept is }(0, −3)} \end{array}\)
تحتوي الخطوط على نفس المنحدر\(y\) وحواجز مختلفة وبالتالي فهي متوازية. قد ترغب في رسم الخطوط البيانية لتأكيد ما إذا كانت متوازية.
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(2x+5y=5\) والخطوط\(y=−\frac{2}{5}x−4\) متوازية.
- إجابة
-
موازى
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(4x−3y=6\) والخطوط\(y=\frac{4}{3}x−1\) متوازية.
- إجابة
-
موازى
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(y=−4\) والخطوط\(y=3\) متوازية.
- إجابة
-
\(\begin{array}{llll}{\text{Write each equation in slope-intercept form.}} &{y=-4} & {\text { and }} &{ y=3} \\ {\text{Since there is no }x\text{ term we write }0x.} &{y=0 x-4} & {} &{y=0 x+3} \\ {\text{Identify the slope and }y\text{-intercept of both lines.}} &{y=m x+b} &{} & {y=m x+b} \\ {} &{m=0} &{} & {m=0} \\{} & {y\text {-intercept is }(0,4)} &{} & {y \text {-intercept is }(0,3)}\end{array}\)
تحتوي الخطوط على نفس المنحدر\(y\) وحواجز مختلفة وبالتالي فهي متوازية.
هناك طريقة أخرى يمكنك من خلالها إلقاء نظرة على هذا المثال. إذا أدركت على الفور من المعادلات أن هذه خطوط أفقية، فأنت تعلم أن منحدرهما هما كلاهما\(0\). نظرًا لأن الخطوط الأفقية تعبر\(y\) المحور السيني عند\(y=−4\) وعند\(y=3\)، فإننا نعلم\(y\) أن نقاط التقاطع هي\((0,−4)\) و\((0,3)\). تحتوي الخطوط على نفس المنحدر\(y\) وحواجز مختلفة وبالتالي فهي متوازية.
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(y=8\) والخطوط\(y=−6\) متوازية.
- إجابة
-
موازى
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(y=1\) والخطوط\(y=−5\) متوازية.
- إجابة
-
موازى
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(x=−2\) والخطوط\(x=−5\) متوازية.
- إجابة
-
\[x=-2 \text { and } x=-5\]
نظرًا لعدم وجود\(y\) المعادلة، لا يمكن وضع المعادلات في شكل منحدر - تقاطع. لكننا نعترف بها كمعادلات للخطوط الرأسية. \(x\)اعتراضاتهم هي\(−2\) و\(−5\). نظرًا\(x\) لاختلاف تقاطعاتها، تكون الخطوط الرأسية متوازية.
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(x=1\) والخطوط\(x=−5\) متوازية.
- إجابة
-
موازى
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(x=8\) والخطوط\(x=−6\) متوازية.
- إجابة
-
موازى
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(y=2x−3\) والخطوط\(−6x+3y=−9\) متوازية. قد ترغب في رسم هذه الخطوط أيضًا لترى كيف تبدو.
- إجابة
-
\(\begin{array} {llll} {\text { The first equation is already in slope-intercept form. }} & {y=2x-3}&{}&{} \\ \\ {\text { Solve the second equation for } y} & {-6x+3y} &{=}&{-9} \\{} & {3y}&{=}&{6x-9} \\ {}&{\frac{3y}{3} }&{=}&{\frac{6x-9}{3}} \\{} & {y}&{=}&{2x-3}\end{array}\)
المعادلة الثانية الآن في شكل منحدر - تقاطع أيضًا.
حدد المنحدر والجزء\(y\) المقطوع لكلا الخطين.
\[\begin{array}{lll}{y=2x-3} &{} & {y=2x-3} \\ {y=mx+b} &{} & {y=mx+b} \\ {m=2} &{} & {m=2} \\ {\text{The }y\text{-intercept is }(0 ,−3)} &{} & {\text{The }y\text{-intercept is }(0 ,−3)} \end{array} \nonumber\]
تحتوي الخطوط على نفس المنحدر، ولكن لها أيضًا نفس\(y\) نقاط التقاطع. تمثل معادلاتهما نفس الخط. إنها ليست متوازية؛ إنها نفس الخط.
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(y=−\frac{1}{2}x−1\) والخطوط\(x+2y=2\) متوازية.
- إجابة
-
غير متوازي؛ نفس الخط
استخدم المنحدرات\(y\) ونقاط التقاطع لتحديد ما إذا كانت الخطوط\(y=\frac{3}{4}x−3\) والخطوط\(3x−4y=12\) متوازية.
- إجابة
-
غير متوازي؛ نفس الخط
استخدم المنحدرات لتحديد الخطوط العمودية
دعونا ننظر إلى الخطوط التي معادلاتها هي\(y=\frac{1}{4}x−1\) و\(y=−4x+2\)، كما هو موضح في الشكل\(\PageIndex{5}\).
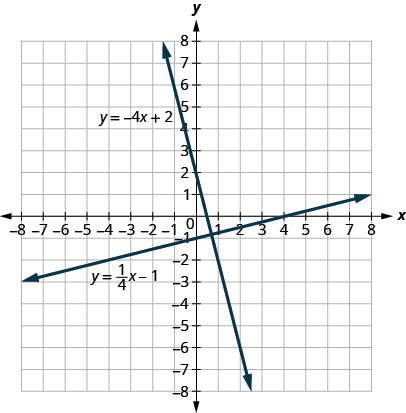
تقع هذه الخطوط في نفس المستوى وتتقاطع في الزوايا الصحيحة. نسمي هذه الخطوط العمودية.
ماذا تلاحظ عن منحدرات هذين الخطين؟ عندما نقرأ من اليسار إلى اليمين،\(y=14x−1\) يرتفع الخط، وبالتالي فإن ميله إيجابي. \(y=−4x+2\)ينخفض الخط من اليسار إلى اليمين، لذلك يكون له منحدر سلبي. هل يعقل لك أن منحدرات خطين عموديين ستحتوي على علامات معاكسة؟
إذا نظرنا إلى ميل الخط الأول\(m_{1}=14\)، ومنحدر الخط الثاني\(m_{2}=−4\)، يمكننا أن نرى أنهما تبادلات سالبة لبعضهما البعض. إذا قمنا بمضاعفتها، فإن منتجها هو\(−1\).
\[\begin{array}{c}{m_{1} \cdot m_{2}} \\ {\frac{1}{4}(-4)} \\ {-1}\end{array}\]
هذا صحيح دائمًا بالنسبة للخطوط العمودية ويقودنا إلى هذا التعريف.
الخطوط العمودية هي خطوط في نفس المستوى تشكل زاوية قائمة.
إذا كانت m1 و m2 هي منحدرات خطين عموديين، ثم:
\[m_{1} \cdot m_{2}=-1 \text { and } m_{1}=\frac{-1}{m_{2}}\]
دائمًا ما تكون الخطوط الرأسية والخطوط الأفقية متعامدة مع بعضها البعض.
تمكنا من النظر إلى شكل المنحدر - التقاطع للمعادلات الخطية وتحديد ما إذا كانت الخطوط متوازية أم لا. يمكننا أن نفعل نفس الشيء للخطوط العمودية.
نجد صيغة المنحدر - التقاطع للمعادلة، ثم نرى ما إذا كانت المنحدرات عبارة عن تبادلات سالبة. إذا كان ناتج المنحدرات هو\(−1\)، تكون الخطوط متعامدة. قد تحتوي الخطوط العمودية على\(y\) نفس التقاطعات.
استخدم المنحدرات لتحديد ما إذا كانت الخطوط\(y=−5x−4\) والخطوط\(x−5y=5\) متعامدة.
- إجابة
-
المعادلة الأولى موجودة بالفعل في شكل منحدر:\(\quad y=−5x−4\)
\(\begin{array} {llll} {\text{Solve the second equation for }y.} &{x-5y} &{=} &{5} \\{} &{-5 y} &{=} &{-x+5} \\ {} & {\frac{-5 y}{-5}} &{=} &{\frac{-x+5}{-5}} \\ {} &{y} &{=} &{\frac{1}{5} x-1} \end{array}\)المعادلة الثانية الآن في شكل تقاطع منحدر أيضًا.
\(\begin{array} {lrllllll} {\text{Identify the slope of each line.}} &{y} &{=} &{-5 x-4} & {} &{y} &{=} &{\frac{1}{5} x-1} \\ {} &{y} &{=} &{m x+b} & {} &{y} &{=} &{m x+b}\\ {} &{m_{1}} &{=}&{-5} & {} &{m_{2}} &{=}&{\frac{1}{5}}\end{array}\)
المنحدرات عبارة عن تبادلات سالبة لبعضها البعض، لذا تكون الخطوط متعامدة. نتحقق من ذلك بضرب المنحدرات،
\[\begin{array}{l}{m_{1} \cdot m_{2}} \\ {-5\left(\frac{1}{5}\right)} \\ {-1\checkmark}\end{array}\]
استخدم المنحدرات لتحديد ما إذا كانت الخطوط\(y=−3x+2\) والخطوط\(x−3y=4\) متعامدة.
- إجابة
-
عمودي
استخدم المنحدرات لتحديد ما إذا كانت الخطوط\(y=2x−5\) والخطوط\(x+2y=−6\) متعامدة.
- إجابة
-
عمودي
استخدم المنحدرات لتحديد ما إذا كانت الخطوط\(7x+2y=3\) والخطوط\(2x+7y=5\) متعامدة.
- إجابة
-
\(\begin{array}{lrlrl}{\text{Solve the equations for y.}} &{7 x+2 y} & {=3} & {2 x+7 y}&{=}&{5} \\{} & {2 y} & {=-7 x+3} & {7 y}&{=}&{-2 x+5} \\ {} &{\frac{2 y}{2}} & {=\frac{-7 x+3}{2} \quad} & {\frac{7 y}{7}}&{=}&{\frac{-2 x+5}{7}} \\ {} &{y} & {=-\frac{7}{2} x+\frac{3}{2}} &{y}&{=}&{\frac{-2}{7}x + \frac{5}{7}}\\ \\{\text{Identify the slope of each line.}} & {y}&{=m x+b} &{y}&{=}&{m x+b} \\{} & {m_{1}} & {=-\frac{7}{2} }&{ m_{2}}&{=}&{-\frac{2}{7}}\end{array}\)
المنحدرات عبارة عن تبادلات لبعضها البعض، لكن لها نفس العلامة. نظرًا لأنها ليست تبادلات سالبة، فإن الخطوط ليست متعامدة.
استخدم المنحدرات لتحديد ما إذا كانت الخطوط\(5x+4y=1\) والخطوط\(4x+5y=3\) متعامدة.
- إجابة
-
غير عمودي
استخدم المنحدرات لتحديد ما إذا كانت الخطوط\(2x−9y=3\) والخطوط\(9x−2y=1\) متعامدة.
- إجابة
-
غير عمودي
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام الرسوم البيانية.
المفاهيم الرئيسية
- شكل المنحدر - المقطوع لمعادلة خط مستقيم بمنحدر مم ونقطة\(y\) تقاطع -\((0,b)\) يساوي،\(y=mx+b\).
- رسم خط مستقيم باستخدام ميله والجزء\(y\) المقطوع منه
- أوجد شكل التقاطع المنحدر لمعادلة الخط المستقيم.
- حدد المنحدر وقم\(y\) بالتقاطع.
- ارسم\(y\) نقطة التقاطع.
- استخدم صيغة المنحدر\(m = \dfrac{\text{rise}}{\text{run}}\) لتحديد الارتفاع والجري.
- بدءًا من\(y\) نقطة التقاطع، قم بحساب الارتفاع والجري لتحديد النقطة الثانية.
- قم بتوصيل النقاط بخط.
- إستراتيجية اختيار الطريقة الأكثر ملاءمة لرسم خط: ضع في اعتبارك شكل المعادلة.
- إذا كان يحتوي على متغير واحد فقط، فهو خط عمودي أو أفقي.
\(x = a\)هو خط عمودي يمر عبر\(x\) المحور -عند a.
\(y = b\) هو خط أفقي يمر عبر\(y\) المحور -at\(b\). - إذا\(y\) تم عزله على أحد طرفي المعادلة، في النموذج\(y=mx+b\)، قم بالرسم البياني باستخدام المنحدر\(y\) والجزء المقطوع.
حدد المنحدر والجزء\(y\) المقطوع ثم قم بالرسم البياني. - إذا كانت المعادلة من النموذج\(Ax+By=C\)، فأوجد القطع المقطوعة.
ابحث عن\(y\) نقاط التقاطع\(x\) - و -، والنقطة الثالثة، ثم الرسم البياني.
- إذا كان يحتوي على متغير واحد فقط، فهو خط عمودي أو أفقي.
- الخطوط المتوازية هي خطوط في نفس المستوى لا تتقاطع.
- تحتوي الخطوط المتوازية على نفس المنحدر\(y\) وحواجز مختلفة.
- إذا كانت منحدرات خطين متوازيين\(m_1\) وما\(m_2\) زالت كذلك\(m_1 = m_2\).
- تحتوي الخطوط العمودية المتوازية على\(x\) تقاطعات مختلفة.
- الخطوط العمودية هي خطوط في نفس المستوى تشكل زاوية قائمة.
- إذا كانت\(m_1\) منحدرات خطين عموديين كذلك، ثم\(m_1\cdot m_2=−1\) و\(m_1=\frac{−1}{m_2}\).\(m_2\)
- دائمًا ما تكون الخطوط الرأسية والخطوط الأفقية متعامدة مع بعضها البعض.
مسرد المصطلحات
- خطوط متوازية
- خطوط في نفس المستوى لا تتقاطع.
- خطوط عمودية
- الخطوط في نفس المستوى التي تشكل الزاوية اليمنى.
- شكل المنحدر المقطوع لمعادلة الخط المستقيم
- شكل المنحدر - المقطوع لمعادلة خط مستقيم بمنحدر مم ونقطة\(y\) تقاطع -\((0,b)\) يساوي،\(y=mx+b\).


