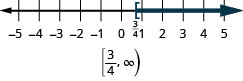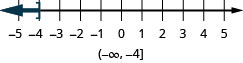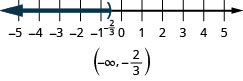2.7: حل المتباينات الخطية
- Page ID
- 200230
في نهاية هذا القسم، ستكون قادرًا على:
- تباينات الرسم البياني على خط الأعداد
- حل المتباينات باستخدام خاصيّ الطرح والجمع للتفاوت
- حل عدم المساواة باستخدام خواص القسمة والضرب لعدم المساواة
- حل عدم المساواة التي تتطلب التبسيط
- ترجم إلى عدم المساواة وقم بحلها
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- ترجم من الجبر إلى اللغة الإنجليزية:\(15>x\).
إذا فاتتك هذه المشكلة، راجع التمرين 1.3.1. - حل:\(n−9=−42\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.1.7. - حل:\(−5p=−23\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.2.1. - حل:\(3a−12=7a−20\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.3.22.
متباينات التمثيل البياني على خط الأعداد
هل تتذكر ما يعنيه أن يكون الرقم حلاً للمعادلة؟ حل المعادلة هو قيمة المتغير الذي يصنع بيانًا صحيحًا عند استبداله بالمعادلة.
ماذا عن حل عدم المساواة؟ ما الرقم الذي يجعل عدم المساواة\(x > 3\) حقيقة؟ هل تفكر في أن «x يمكن أن تكون 4"؟ هذا صحيح، ولكن يمكن أن تكون x 5 أيضًا، أو 20، أو حتى 3.001. أي رقم أكبر من 3 هو حل لعدم المساواة\(x > 3\).
نعرض حلول عدم المساواة\(x > 3\) على خط الأعداد من خلال تظليل جميع الأرقام على يمين 3، لإظهار أن جميع الأرقام الأكبر من 3 هي حلول. نظرًا لأن الرقم 3 نفسه ليس حلاً، فقد وضعنا قوسًا مفتوحًا عند 3. يظهر الرسم البياني في الشكل\(\PageIndex{1}\).\(x > 3\) يرجى ملاحظة أنه يتم استخدام الاصطلاح التالي: تشير الأسهم ذات اللون الأزرق الفاتح في الاتجاه الإيجابي وتشير الأسهم الزرقاء الداكنة في الاتجاه السلبي.
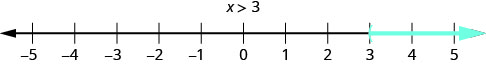
الرسم البياني لعدم المساواة\(x \geq 3\) يشبه إلى حد كبير الرسم البياني لـ\(x > 3\)، لكننا الآن بحاجة إلى إظهار أن الرقم 3 هو الحل أيضًا. نقوم بذلك عن طريق وضع قوس\(x = 3\)، كما هو موضح في الشكل\(\PageIndex{2}\).
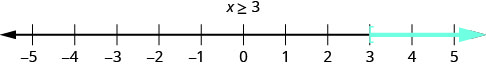
لاحظ أن رمز الأقواس المفتوحة، (، يوضح أن نقطة نهاية عدم المساواة غير مضمنة. يُظهر رمز القوس المفتوح، [، أن نقطة النهاية مضمنة.
رسم بياني على خط الأرقام:
- \(x\leq 1\)
- \(x<5\)
- \(x>−1\)
- إجابة
-
1. \(x\leq 1\)هذا يعني جميع الأرقام التي تقل عن أو تساوي 1. نقوم بتظليل جميع الأرقام الموجودة على خط الأرقام على يسار 1 ونضع قوسًا عند x=1 لإظهار أنه مضمن.
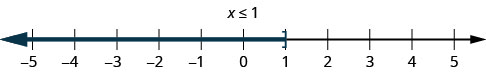
2. \(x<5\)هذا يعني جميع الأرقام الأقل من 5، ولكن ليس بما في ذلك 5. نقوم بتظليل جميع الأرقام الموجودة على خط الأعداد على يسار 5 ونضع قوسًا عند x=5 لإظهار أنها غير مضمنة.
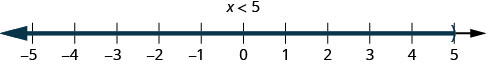
3. \(x>−1\)وهذا يعني جميع الأرقام الأكبر من −1، ولكن ليس بما في ذلك −1. نضع التظليل في جميع الأرقام على خط الأعداد على يمين −1، ثم نضع قوسًا عند x=−1 لإظهار أنها غير مضمنة.
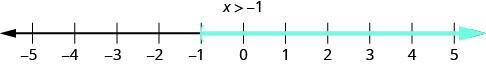
رسم بياني على خط الأرقام:
- \(x\leq −1\)
- \(x>2\)
- \(x<3\)
- إجابة
-
رسم بياني على خط الأرقام:
- \(x>−2\)
- \(x<−3\)
- \(x\geq −1\)
- إجابة
-
يمكننا أيضًا تمثيل عدم المساواة باستخدام الترميز الفاصل الزمني. كما رأينا أعلاه، فإن عدم المساواة\(x>3\) يعني جميع الأرقام الأكبر من 3. لا يوجد حد أعلى لحل عدم المساواة هذا. في الترميز الفاصل الزمني، نعبر عن\(x>3\) كـ\((3, \infty)\). \(\infty\)تتم قراءة الرمز باسم «اللانهاية». إنه ليس رقمًا فعليًا. \(\PageIndex{3}\)يوضح الشكل كلاً من خط الأرقام وترميز الفاصل الزمني.

عدم المساواة\(x\leq 1\) يعني جميع الأرقام التي تقل عن أو تساوي 1. لا يوجد حد أدنى لهذه الأرقام. نكتب\(x\leq 1\) بالتدوين الفاصل الزمني كـ\((-\infty, 1]\). \(-\infty\)تتم قراءة الرمز على أنه «اللانهاية السالبة». \(\PageIndex{4}\)يوضح الشكل كلاً من خط الأرقام والترميز الفاصل الزمني.


هل لاحظت كيف يتطابق القوس أو القوس في ترقيم الفاصل الزمني مع الرمز الموجود في نقطة نهاية السهم؟ تظهر هذه العلاقات في الشكل\(\PageIndex{5}\).

رسم بياني على خط الأعداد واكتب بتدوين الفاصل الزمني.
- \(x \geq -3\)
- \(x<2.5\)
- \(x\leq \frac{3}{5}\)
- إجابة
-
1.
2.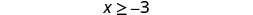
ظلل على يمين −3، ثم ضع قوسًا عند −3. 
اكتب بالتدوين الفاصل الزمني. 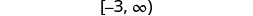
3.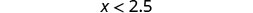
ظلل على يسار 2.5، ثم ضع قوسًا عند 2.5. 
اكتب بالتدوين الفاصل الزمني. 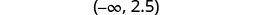
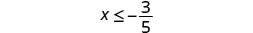
ظلل على يسار الصورة\(-\frac{3}{5}\)، ثم ضع قوسًا عليها\(-\frac{3}{5}\). 
اكتب بالتدوين الفاصل الزمني. 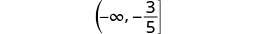
رسم بياني على خط الأعداد واكتب بتدوين الفاصل الزمني:
- \(x>2\)
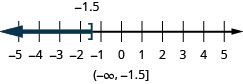
- \(x\leq −1.5\)
- \(x\geq \frac{3}{4}\)
- إجابة
-
رسم بياني على خط الأعداد واكتب بتدوين الفاصل الزمني:
- \(x\leq −4\)
- \(x\geq 0.5\)
- \(x<-\frac{2}{3}\)
- إجابة
-
حل المتباينات باستخدام خواص الطرح والجمع للتفاوت
تنص خاصيتا الطرح والجمع للمساواة على أنه إذا تساوت كميتان، فعندما نجمع أو نطرح نفس الكمية من كلتا الكميتين، ستكون النتائج متساوية.
\[\begin{array} { l l } { \textbf { Subtraction Property of Equality } } & { \textbf { Addition Property of Equality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if } \qquad \quad a = b , } & { \text { if } \qquad \quad a = b } \\ { \text { then } a - c = b - c . } & { \text { then } a + c = b + c } \end{array}\]
تنطبق الخصائص المماثلة على عدم المساواة.
| على سبيل المثال، نعلم أن −4 أقل من 2. | 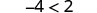 |
| إذا طرحنا 5 من كلتا الكميتين، فهل يظل الجانب الأيسر أقل من الجانب الأيمن؟ | 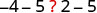 |
| نحصل على −9 على اليسار و−3 على اليمين. |  |
| ونعلم أن −9 أقل من −3. |  |
|
بقيت علامة عدم المساواة كما هي. |
وبالمثل يمكننا أن نظهر أن عدم المساواة يظل أيضًا كما هو بالنسبة للإضافة.
هذا يقودنا إلى خصائص الطرح والجمع لعدم المساواة.
\[\begin{array} { l l } { \textbf { Subtraction Property of Inequality } } & { \textbf { Addition Property of Inequality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if }\qquad \quad a < b } & { \text { if } \qquad \quad a < b } \\ { \text { then } a - c < b - c . } & { \text { then } a + c < b + c } \\\\ { \text { if } \qquad \quad a > b } & { \text { if } \qquad \quad a > b } \\ { \text { then } a - c > b - c . } & { \text { then } a + c > b + c } \end{array}\]
نحن نستخدم هذه الخصائص لحل المتباينات، مع اتخاذ نفس الخطوات التي استخدمناها لحل المعادلات. لحل عدم المساواة\(x+5>9\)، ستبدو الخطوات كما يلي:
\[\begin{array}{rrll} {} &{x + 5} &{ >} &{9} \\ {\text{Subtract 5 from both sides to isolate }x.} &{x + 5 - 5} &{ >} &{9 - 5} \\{} &{x} &{ >} &{4} \\ \end{array}\]
أي رقم أكبر من 4 هو حل لهذا التفاوت.
حل عدم المساواة\(n - \frac{1}{2} \leq \frac{5}{8}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
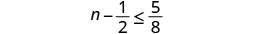
أضف\(\frac{1}{2}\) إلى كلا جانبي عدم المساواة. 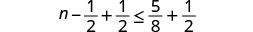
قم بالتبسيط. 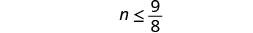
ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني.
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(p - \frac{3}{4} \geq \frac{1}{6}\)
- إجابة
-
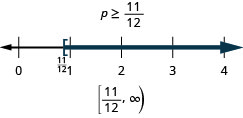
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(r - \frac{1}{3} \leq \frac{7}{12}\)
- إجابة
-
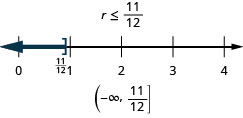
حل المتباينات باستخدام خواص القسمة والضرب في عدم المساواة
تنص خصائص القسمة والضرب للمساواة على أنه إذا تساوت كميتان، فعندما نقسم أو نضرب كلتا الكميتين بنفس المقدار، ستكون النتائج متساوية أيضًا (بشرط ألا نقسم على 0).
\[\begin{array}{ll} {\textbf{Division Property of Equality}} &{\textbf{MUltiplication Property of Equality}} \\ {\text{For any numbers a, b, c, and c} \neq 0} &{\text{For any numbers a, b, c}} \\ {\text{if } \qquad a = b} &{\text{if} \qquad \quad a = b} \\ {\text{then }\quad \frac{a}{c} = \frac{b}{c}} &{\text{then } \quad ac = bc} \end{array}\]
هل هناك خصائص مماثلة لعدم المساواة؟ ماذا يحدث لعدم المساواة عندما نقسم أو نضرب كلا الجانبين بثابت؟
فكر في بعض الأمثلة العددية.
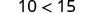 |
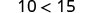 |
||
| قسّم كلا الجانبين على 5. | 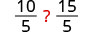 |
اضرب كلا الجانبين في 5. |  |
| قم بالتبسيط. |  |
 |
|
| املأ علامات عدم المساواة. |  |
 |
بقيت علامات عدم المساواة كما هي.
هل تظل اللامساواة كما هي عندما نقسم أو نضرب عددًا سالبًا؟
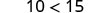 |
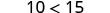 |
||
| قسّم كلا الجانبين بنسبة -5. | 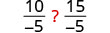 |
اضرب كلا الجانبين في -5. |  |
| قم بالتبسيط. |  |
 |
|
| املأ علامات عدم المساواة. |  |
 |
عكست علامات عدم المساواة اتجاهها.
عندما نقسم أو نضرب عدم المساواة في رقم موجب، تظل علامة عدم المساواة كما هي. عندما نقسم أو نضرب عدم المساواة برقم سالب، تنعكس علامة عدم المساواة.
فيما يلي خصائص القسمة والضرب لعدم المساواة للرجوع إليها بسهولة.
لأي أرقام حقيقية أ، ب، ج
\[\begin{array}{ll} {\text{if } a < b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \\ {\text{if } a > b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a < b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a > b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \end{array}\]
عندما نقسم أو نضرب عدم المساواة بـ:
- الرقم الموجب، يبقى عدم المساواة كما هو.
- الرقم السالب، ينعكس عدم المساواة.
حل عدم المساواة\(7y<42\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
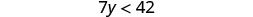
قسّم جانبي عدم المساواة على 7.
منذ ذلك الحين\(7>0\)، يبقى عدم المساواة على حاله.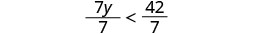
قم بالتبسيط. 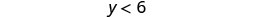
ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. 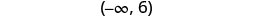
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(9c>72\)
- إجابة
-
\(c>8\)

\((8, \infty)\)
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(12d\leq 60\)
- إجابة
-
\(d\leq 5\)

\((-\infty, 5]\)
حل عدم المساواة\(−10a\geq 50\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
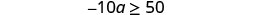
قسّم كلا جانبي عدم المساواة على −10.
منذ\(−10<0\) ذلك الحين، ينعكس عدم المساواة.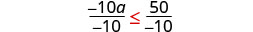
قم بالتبسيط. 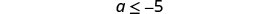
ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. 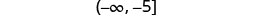
حل كل تفاوت، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(−8q<32\)
- إجابة
-
\(q>−4\)
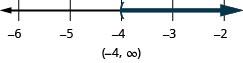
حل كل تفاوت، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(−7r\leq −70\)
- إجابة
-
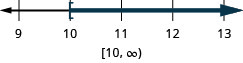
في بعض الأحيان عند حل عدم المساواة، ينتهي المتغير على اليمين. يمكننا إعادة كتابة عدم المساواة في الاتجاه المعاكس للحصول على المتغير إلى اليسار.
\[\begin{array}{l} x > a\text{ has the same meaning as } a < x \end{array}\]
فكر في الأمر على أنه «إذا كان Xavier أطول من أليكس، فإن أليكس أقصر من Xavier».
حل عدم المساواة\(-20 < \frac{4}{5}u\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
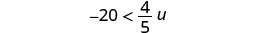
اضرب كلا جانبي عدم المساواة في\(\frac{5}{4}\).
منذ ذلك الحين\(\frac{5}{4} > 0\)، يبقى عدم المساواة على حاله.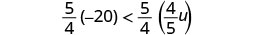
قم بالتبسيط. 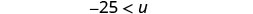
أعد كتابة المتغير الموجود على اليسار. 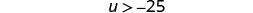
ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. 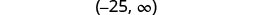
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(24 \leq \frac{3}{8}m\)
- إجابة
-
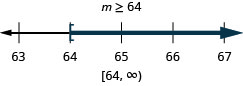
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(-24 < \frac{4}{3}n\)
- إجابة
-
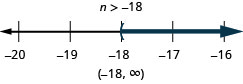
حل عدم المساواة\(\frac{t}{-2} \geq 8\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
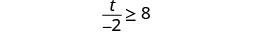
اضرب كلا جانبي عدم المساواة في −2.
منذ\(−2<0\) ذلك الحين، ينعكس عدم المساواة.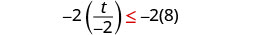
قم بالتبسيط. 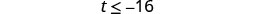
ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. 
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(\frac{k}{-12}\leq 15\)
- إجابة
-
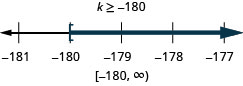
حل عدم المساواة، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
\(\frac{u}{-4}\geq -16\)
- إجابة
-
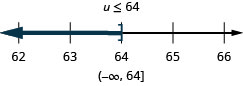
حل عدم المساواة التي تتطلب التبسيط
ستستغرق معظم حالات عدم المساواة أكثر من خطوة لحلها. نحن نتبع نفس الخطوات التي استخدمناها في الاستراتيجية العامة لحل المعادلات الخطية، ولكن تأكد من إيلاء اهتمام وثيق أثناء الضرب أو القسمة.
حل عدم المساواة\(4m\leq 9m+17\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
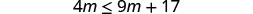
اطرح 9 أمتار من كلا الجانبين لتجميع المتغيرات الموجودة على اليسار. 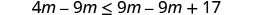
قم بالتبسيط. 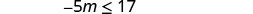
قسّم كلا جانبي عدم المساواة على −5، وعكسوا عدم المساواة. 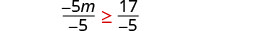
قم بالتبسيط. 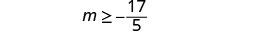
ارسم حلًا بيانيًا على خط الأعداد. 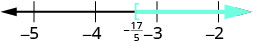
اكتب الحل بالتدوين الفاصل الزمني. 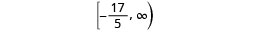
حل عدم المساواة\(3q\geq 7q−23\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
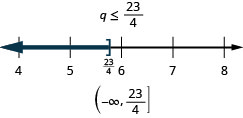
حل عدم المساواة\(6x<10x+19\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
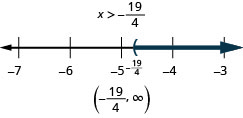
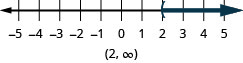
حل حل حل\(8p+3(p−12)>7p−28\) التمثيل البياني للتفاوت على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
قم بتبسيط كل جانب قدر الإمكان. 8p+3 (p−12) >7p−28 توزيع. 8 ص+3p−36> 7p−28 اجمع بين المصطلحات المتشابهة. 11p−36>7p−28 اطرح 7p من كلا الجانبين لتجميع المتغيرات الموجودة على اليسار. 11p−36-7p>7p−28-7p قم بالتبسيط. 4p−36>−28 أضف 36 إلى كلا الجانبين لجمع الثوابت على اليمين. 4p−36+36>−28+36 قم بالتبسيط. 4p>8 قسّم كلا جانبي عدم المساواة على 4؛ يبقى عدم المساواة كما هو. \(\frac{4p}{4}>84\) قم بالتبسيط. \(p>2\) ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. \((2, \infty)\)
حل عدم المساواة\(9y+2(y+6)>5y−24\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
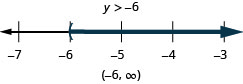
حل عدم المساواة\(6u+8(u−1)>10u+32\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
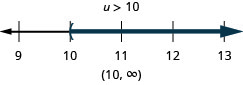
تمامًا مثل بعض المعادلات عبارة عن هويات وبعضها تناقضات، قد تكون أوجه عدم المساواة هويات أو تناقضات أيضًا. نحن ندرك هذه الأشكال عندما يتبقى لنا ثوابت فقط أثناء حل عدم المساواة. إذا كانت النتيجة عبارة صحيحة، فلدينا هوية. إذا كانت النتيجة عبارة خاطئة، فلدينا تناقض.
حل عدم المساواة\(8x−2(5−x)<4(x+9)+6x\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
قم بتبسيط كل جانب قدر الإمكان. 8x−2 (5−x) <4 (x+9) +6x توزيع. 8x−10+2 × <4x+36+6x اجمع بين المصطلحات المتشابهة. 10x−10<10x+36 اطرح 10x من كلا الجانبين لتجميع المتغيرات الموجودة على اليسار. 10x−10−10x<10x+36−10x قم بالتبسيط. −10<36 اختفت xx، ولدينا بيان حقيقي. عدم المساواة هي هوية.
الحل هو جميع الأرقام الحقيقية.ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. \((-\infty, \infty)\)
حل عدم المساواة\(4b−3(3−b)>5(b−6)+2b\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
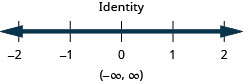
حل عدم المساواة\(9h−7(2−h)<8(h+11)+8h\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
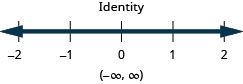
حل عدم المساواة\(\frac{1}{3}a - \frac{1}{8}a > \frac{5}{24}a + \frac{3}{4}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
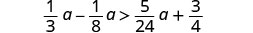
اضرب كلا الجانبين في شاشة LCD، 24، لمسح الكسور. 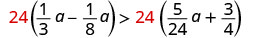
قم بالتبسيط. 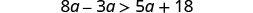
اجمع بين المصطلحات المتشابهة. 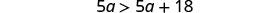
اطرح 5a من كلا الجانبين لتجميع المتغيرات الموجودة على اليسار. 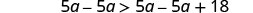
قم بالتبسيط. 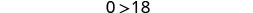
البيان خاطئ! عدم المساواة هو تناقض. لا يوجد حل. ارسم حلًا بيانيًا على خط الأعداد. 
اكتب الحل بالتدوين الفاصل الزمني. لا يوجد حل.
حل عدم المساواة\(\frac{1}{4}x - \frac{1}{12}x > \frac{1}{6}x + \frac{7}{8}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
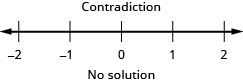
حل عدم المساواة\(\frac{2}{5}z - \frac{1}{3}z < \frac{1}{15}z - \frac{3}{5}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.
- إجابة
-
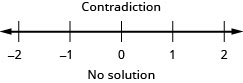
ترجم إلى عدم المساواة وحلّها
لترجمة الجمل الإنجليزية إلى تفاوتات، نحتاج إلى التعرف على العبارات التي تشير إلى عدم المساواة. بعض الكلمات سهلة، مثل «أكثر من» و «أقل من». لكن البعض الآخر ليس واضحًا.
فكر في عبارة «على الأقل» - ماذا يعني أن يكون عمرك «21 عامًا على الأقل»؟ يعني 21 أو أكثر. عبارة «على الأقل» هي نفس عبارة «أكبر من أو تساوي».
\(\PageIndex{4}\)[1]يعرض الجدول بعض العبارات الشائعة التي تشير إلى عدم المساواة.
| > | \(\geq\) | < | \(\leq\) |
|---|---|---|---|
| فئة «data-valign=» middle = «lt-math-15134">أكبر من | \ (\ geq\)» data-valign= «middle» class="lt-math-15134">أكبر من أو يساوي | أقل من | \ (\ leq\)» data-valign= «middle» class="lt-math-15134">أقل من أو يساوي |
| فئة «data-valign=» middle = «lt-math-15134">هي أكثر من | \ (\ geq\)» data-valign= «middle» class="lt-math-15134">على الأقل | أصغر من | \ (\ leq\)» data-valign= «middle» class="lt-math-15134">على الأكثر |
| فئة «data-valign=» middle = «lt-math-15134">أكبر من | \ (\ geq\)» data-valign= «middle» class="lt-math-15134">لا تقل عن | لديه أقل من | \ (\ leq\)» data-valign= «middle» class="lt-math-15134">لا تزيد عن |
| فئة «data-valign=» middle = «lt-math-15134">تتجاوز | \ (\ geq\)» data-valign= «middle» class="lt-math-15134">هو الحد الأدنى | أقل من | \ (\ leq\)» data-valign= «middle» class="lt-math-15134">هو الحد الأقصى |
قم بالترجمة والحل. ثم اكتب الحل في تدوين الفاصل الزمني والرسم البياني على خط الأعداد.
اثنا عشر مرة في c لا تزيد عن 96.
- إجابة
-
ترجم. 
الحل - قسّم كلا الجانبين بمقدار 12. 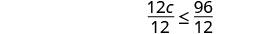
قم بالتبسيط. 
اكتب بالتدوين الفاصل الزمني. 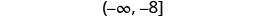
رسم بياني على خط الأعداد. 
قم بالترجمة والحل. ثم اكتب الحل في تدوين الفاصل الزمني والرسم البياني على خط الأعداد.
عشرون مرة y هي 100 على الأكثر
- إجابة
-
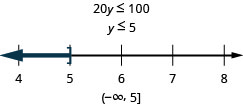
قم بالترجمة والحل. ثم اكتب الحل في تدوين الفاصل الزمني والرسم البياني على خط الأعداد.
تسع مرات z لا تقل عن 135
- إجابة
-
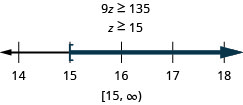
قم بالترجمة والحل. ثم اكتب الحل في تدوين الفاصل الزمني والرسم البياني على خط الأعداد.
أقل بثلاثين من x يساوي 45 على الأقل.
- إجابة
-
ترجم. 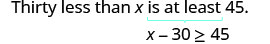
الحل - أضف 30 إلى كلا الجانبين. 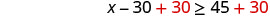
قم بالتبسيط. 
اكتب بالتدوين الفاصل الزمني. 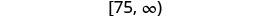
رسم بياني على خط الأعداد. 
قم بالترجمة والحل. ثم اكتب الحل في تدوين الفاصل الزمني والرسم البياني على خط الأعداد.
تسعة عشر أقل من p لا تقل عن 47
- إجابة
-
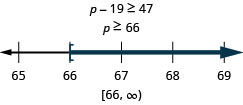
قم بالترجمة والحل. ثم اكتب الحل في تدوين الفاصل الزمني والرسم البياني على خط الأعداد.
أربعة أكثر من a يساوي 15 على الأكثر.
- إجابة
-
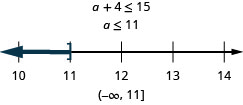
المفاهيم الرئيسية
- خاصية الطرح في عدم المساواة
بالنسبة لأي أعداد أ، ب، ج،
إذا كانت a<b ثم a−c<b−c
وإذا a>b ثم a−c>b−c. - خاصية إضافة عدم المساواة
لأي أرقام a و b و c،
إذا كانت a<b ثم a+c<b+c
وإذا a>b ثم a+c>b+c. - خصائص القسمة والضرب في عدم المساواة y
بالنسبة لأي أرقام أ، ب، ج،
إذا كانت a <b and c>0، ثم c <bc and ac>bc.
إذا كان a> b و c>0، ثم ac>bc و ac>bc.
إذا كان <b و cbc<0, then ac> و ac>bc.
إذا كان a>b و c <0، ثم ac<bc و ac<bc. - عندما نقسم أو نضرب عدم المساواة بـ:
- الرقم الموجب، يبقى عدم المساواة كما هو.
- الرقم السالب، ينعكس عدم المساواة.