1.10: خصائص الأعداد الحقيقية
- Page ID
- 200689
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم الخصائص التبادلية والترابطية
- استخدم الهوية والخصائص العكسية للجمع والضرب
- استخدم خصائص الصفر
- قم بتبسيط التعبيرات باستخدام خاصية التوزيع
يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي يتم تناولها في هذا القسم في فصل ما قبل الجبر، «خصائص الأرقام الحقيقية».
استخدم الخصائص الإبدالية والترابطية
فكر في إضافة رقمين، قل 5 و 3. الترتيب الذي نضيفها به لا يؤثر على النتيجة، أليس كذلك؟
\[\begin{array} { cc } { 5 + 3 } & { 3 + 5 } \\ { 8 } & { 8 } \\ { 5 + 3 = } & { 3 + 5 } \end{array}\]
النتائج هي نفسها.
كما نرى، لا يهم الترتيب الذي نضيف به!
ماذا عن ضرب 5 و 3؟
\[\begin{array} { c c } { 5 \cdot 3 } & { 3 \cdot 5 } \\ { 15 } & { 15 } \\ { 5 \cdot 3=} &{3 \cdot 5 } \end{array}\]
مرة أخرى، النتائج هي نفسها!
الترتيب الذي نضرب به لا يهم!
توضح هذه الأمثلة الخاصية التبادلية. عند الإضافة أو الضرب، فإن تغيير الترتيب يعطي نفس النتيجة.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b \text { are real numbers, then } \quad a + b = b + a } \\ { \textbf { of Multiplication } } & { \text { If } a , b \text { are real numbers, then } \quad a \cdot b = b \cdot a } \end{array}\]
عند الإضافة أو الضرب، فإن تغيير الترتيب يعطي نفس النتيجة.
الخاصية التبادلية لها علاقة بالترتيب. إذا قمت بتغيير ترتيب الأرقام عند الجمع أو الضرب، فإن النتيجة هي نفسها.
ماذا عن الطرح؟ هل الترتيب مهم عندما نطرح الأرقام؟ هل يعطي 7−3 نفس النتيجة مثل 3−7؟
\[\begin{array} { c c } { 7 - 3 } & { 3 - 7 } \\ { 4 } & { - 4 } \end{array}\]
\[\begin{aligned} 4 & \neq - 4 \\ 7 - 3 & \neq 3 - 7 \end{aligned}\]
النتائج ليست هي نفسها.
نظرًا لأن تغيير ترتيب الطرح لا يعطي نفس النتيجة، فنحن نعلم أن الطرح ليس إبداليًا.
دعونا نرى ما يحدث عندما نقسم رقمين. هل التقسيم تبادلي؟
\[\begin{array} { cc} { 12 \div 4 } & { 4 \div 12 } \\ { \frac { 12 } { 4 } } & { \frac { 4 } { 12 } } \\ { 3 } & { \frac { 1 } { 3 } } \end{array}\]
\[\begin{aligned} 3 \neq & \frac { 1 } { 3 } \\ 12 \div 4 & \neq 4 \div 12 \end{aligned}\]
النتائج ليست هي نفسها.
نظرًا لأن تغيير ترتيب القسمة لا يعطي نفس النتيجة، فإن القسمة ليست تبديلية. تنطبق الخصائص التبادلية فقط على الجمع والضرب!
- الجمع والضرب تبديلان.
- الطرح والقسمة لا يتبادلان.
إذا طُلب منك تبسيط هذا التعبير، فكيف ستفعل ذلك وماذا ستكون إجابتك؟
\[7 + 8 + 2\]
قد يعتقد بعض الناس\(7+8\) أنه 15 ثم\(15+2\) 17. قد يبدأ البعض الآخر بالرقم 10 ثم\(7+10\) يصنع 17.\(8+2\)
في كلتا الحالتين تعطي نفس النتيجة. تذكر أننا نستخدم الأقواس كرموز تجميع للإشارة إلى العملية التي يجب إجراؤها أولاً.
\[\begin{array} { ll } { \text{ Add } 7 + 8 . } & { ( 7 + 8 ) + 2 } \\ { \text { Add. } } & { 15 + 2 } \\ { \text { Add. } } & { 17 } \\ \\ { } & { 7 + ( 8 + 2 ) } \\ { \text { Add } 8 + 2 . } & { 7 + 10 } \\ { \text { Add. } } & { 77 } \\\\ { ( 7 + 8 ) + 2 = 7 + ( 8 + 2 ) } \end{array}\]
عند إضافة ثلاثة أرقام، فإن تغيير تجميع الأرقام يعطي نفس النتيجة.
هذا صحيح بالنسبة للضرب أيضًا.
\[\begin{array} { ll } { } & { (5\cdot \frac{1}{3})\cdot 3 } \\ { \text { Multiply. } 5\cdot \frac{1}{3} } & { \frac{5}{3}\cdot 3 } \\ { \text { Multiply. } } & { 5 } \\ \\ { } & { 5\cdot (\frac{1}{3}\cdot 3) } \\ { \text { Multiply. } \frac{1}{3}\cdot 3 } & { 5\cdot 1 } \\ { \text { Multiply. } } & { 5 } \\ \\ { (5\cdot \frac{1}{3})\cdot 3 = 5\cdot (\frac{1}{3}\cdot 3) } \end{array}\]
عند ضرب ثلاثة أرقام، فإن تغيير تجميع الأرقام يعطي نفس النتيجة.
ربما تعرف هذا، لكن المصطلحات قد تكون جديدة بالنسبة لك. توضح هذه الأمثلة الخاصية الترابطية.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b , c \text { are real numbers, then } ( a + b ) + c = a + ( b + c ) } \\ { \textbf { of Multiplication } } & { \text { If } a , b , c \text { are real numbers, then } ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) } \end{array}\]
عند الإضافة أو الضرب، فإن تغيير التجميع يعطي نفس النتيجة.
دعونا نفكر مرة أخرى في الضرب\(5\cdot \frac{1}{3}\cdot 3\). حصلنا على نفس النتيجة في كلا الاتجاهين، ولكن ما هي الطريقة الأسهل؟ يؤدي الضرب\(\frac{1}{3}\) و3 أولاً، كما هو موضح أعلاه على الجانب الأيمن، إلى إزالة الكسر في الخطوة الأولى. يمكن أن يؤدي استخدام الخاصية الترابطية إلى تسهيل الرياضيات!
الخاصية الترابطية لها علاقة بالتجميع. إذا قمنا بتغيير كيفية تجميع الأرقام، فستكون النتيجة هي نفسها. لاحظ أنها نفس الأرقام الثلاثة بنفس الترتيب - الاختلاف الوحيد هو التجميع.
لقد رأينا أن الطرح والقسمة ليسا بديلين. كما أنها ليست ترابطية.
عند تبسيط التعبير، من الجيد دائمًا التخطيط للخطوات التي ستكون. من أجل دمج المصطلحات المتشابهة في المثال التالي، سنستخدم خاصية الإبدال الخاصة بالإضافة لكتابة المصطلحات المتشابهة معًا.
قم بالتبسيط:\(18p+6q+15p+5q\).
- إجابة
-
\[\begin{array} { l l} {} &{18p+6q+15p+5q}\\ \\{ \text { Use the commutative property of addition } } &{} \\ { \text {to re-order so that like terms are together.} } &{18p+15p+ 6q+5q} \\ \\ {\text{Add like terms.}} &{33p + 11q} \end{array}\]
قم بالتبسيط:\(23r+14s+9r+15s\).
- إجابة
-
\(32r+29s\)
قم بالتبسيط:\(37m+21n+4m−15n\).
- إجابة
-
\(41m+6n\)
عندما يتعين علينا تبسيط التعبير الجبري s، يمكننا غالبًا تسهيل العمل من خلال تطبيق الخاصية الإبدالية أو الترابطية أولاً، بدلاً من اتباع ترتيب العمليات تلقائيًا. عند جمع الكسور أو طرحها، اجمع تلك التي لها قاسم مشترك أولاً.
قم بالتبسيط:\((\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}\)
- إجابة
-
\[\begin{array} { l l } {} &{(\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}} \\{ \text { Notice that the last } 2 \text { terms have a } } \\ { \text { common denominator, so change the } } &{\frac { 5 } { 13 } + \left( \frac { 3 } { 4 } + \frac { 1 } { 4 } \right)}\\ { \text { grouping. } } &{}\\ \\ {\text{Add in parentheses first.}} &{\frac{5}{13} + (\frac{4}{4})} \\ \\ {\text{Simplify the fraction.}} &{\frac{5}{13} + 1} \\ \\ {\text{Add.}} &{1\frac{5}{13}} \\ \\ {\text{Convert to an improper fraction.}} &{\frac{18}{13}} \end{array}\]
قم بالتبسيط:\((\frac{7}{15} + \frac{5}{8}) + \frac{3}{8}\)
- إجابة
-
\(1\frac{7}{15}\)
قم بالتبسيط:\((\frac{2}{9} + \frac{7}{12}) + \frac{5}{12}\)
- إجابة
-
\(1\frac{2}{9}\)
استخدم الخاصية الترابطية للتبسيط\(6(3x)\).
- إجابة
-
استخدم الخاصية الترابطية للضرب\((a\cdot b)\cdot c=a\cdot (b\cdot c)\)، لتغيير التجميع.
\[\begin{array} { ll } {} &{ 6 ( 3 x ) } \\ { \text { Change the grouping. } } &{(6\cdot 3)x} \\ { \text { Multiply in the parentheses. } } &{18} \end{array}\]
لاحظ أنه يمكننا الضرب\(6\cdot 3\) ولكن لا يمكننا الضرب\(3x\) دون الحصول على قيمة لـ\(x\).
استخدم الخاصية الترابطية للتبسيط\(8(4x)\).
- إجابة
-
\(32x\)
استخدم الخاصية الترابطية للتبسيط\(-9(7y)\).
- إجابة
-
\(-63y\)
استخدم خصائص الهوية والمعكوس للجمع والضرب
ماذا يحدث عندما نضيف 0 إلى أي رقم؟ لا تؤدي إضافة 0 إلى تغيير القيمة. لهذا السبب، نسمي 0 الهوية الإضافية.
على سبيل المثال،
\[\begin{array} { c c c } { 13 + 0 } & { - 14 + 0 } & { 0 + ( - 8 ) } \\ { 13 } & { - 14 } & { - 8 } \end{array}\]
توضح هذه الأمثلة خاصية الهوية الخاصة بالإضافة التي تنص على ذلك لأي رقم حقيقي\(a\),\(a+0=a\) و\(0+a=a\).
ماذا يحدث عندما نضرب أي رقم في واحد؟ الضرب في 1 لا يغير القيمة. لذلك نسمي 1 الهوية المضاعفة.
على سبيل المثال،\[\begin{array} { r r r } { 43 \cdot 1 } & { - 27 \cdot 1 } & { 1 \cdot \frac { 3 } { 5 } } \\ { 43 } & { - 27 } & { \frac { 3 } { 5 } } \end{array}\]
توضح هذه الأمثلة خاصية الهوية الخاصة بالضرب التي تنص على ذلك لأي رقم حقيقي\(a\)،\(a\cdot 1=a\) و\(1\cdot a=a\).
نحن نلخص خصائص الهوية أدناه.
\[\begin{array} { l l} { \textbf {of addition}\text{ For any real number } a : } &{ a + 0 = a \quad 0 + a = a } \\ { \textbf{0} \text { is the}\textbf{ additive identity } } \\ {\textbf {of multiplication}\text{ For any real number } a : } &{ a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1}\text{ is the}\textbf{ multiplicative identity } } \end{array}\]

لاحظ أنه في كل حالة، كان الرقم المفقود هو عكس الرقم!
نحن نسمي\(−a\). المعكوس الجمعي لـ a. نقيض الرقم هو معكوسه الإضافي. الرقم ونقيضه يضيفان إلى الصفر، وهو الهوية الإضافية. يؤدي هذا إلى خاصية الجمع العكسية التي تنص على أي رقم حقيقي\(a, a+(−a)=0\). تذكر أن الرقم ونقيضه يضيفان إلى الصفر.
ما العدد\(\frac{2}{3}\) مضروبًا في إعطاء الهوية المضاعفة، ١؟ بعبارة أخرى،\(\frac{2}{3}\) أضعاف ما هي النتائج في 1؟

ما العدد مضروبًا في ٢ الذي يُعطي الهوية الضربية، ١؟ بمعنى آخر مرتين ما هي النتائج في 1؟

لاحظ أنه في كل حالة، كان الرقم المفقود هو مقلوب الرقم!
نسمي\(\frac{1}{a}\) المعكوس الضربي لـ a. مقلوب العدد هو معكوسه الضربي. عدد وضربه في واحد، وهو الهوية المضاعفة. يؤدي هذا إلى خاصية الضرب العكسية التي تنص على ذلك لأي رقم حقيقي\(a, a\neq 0, a\cdot \frac{1}{a}=1\).
سنذكر رسميًا الخصائص العكسية هنا:
\[\begin{array} { l l l } { \textbf { of addition } } &{ \text { For any real number } a,} &{a + (-a) = 0}\\{} &{-a \text{. is the}\textbf{ additive inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its opposite add to zero. } }&{}\\ \\{ \textbf { of multiplication } } &{ \text { For any real number } a, a\neq 0} &{a\cdot \frac{1}{a} = 1}\\{} &{\frac{1}{a} \text{. is the}\textbf{ multiplicative inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its reciprocal multiply to zero. } }&{} \end{array}\]
أوجد المعكوس الجمعي لـ
- \(\frac{5}{8}\)
- \(0.6\)
- \(-8\)
- \(-\frac{4}{3}\)
- إجابة
-
لإيجاد المعكوس الجمعي، نجد العكس.
- المعكوس الجمعي لـ\(\frac{5}{8}\) هو عكس\(\frac{5}{8}\). المعكوس الجمعي لـ\(\frac{5}{8}\) هو\(-\frac{5}{8}\)
- المعكوس الجمعي لـ\(0.6\) هو عكس\(0.6\). المعكوس الجمعي لـ\(0.6\) is\(-0.6\).
- المعكوس الجمعي لـ\(-8\) هو عكس\(-8\). نكتب عكس\(-8\) as\(-(-8)\)، ثم نبسطه إلى\(8\). لذلك، فإن المعكوس الجمعي لـ\(-8\) هو\(8\).
- المعكوس الجمعي لـ\(-\frac{4}{3}\) هو عكس\(-\frac{4}{3}\). نكتب هذا كـ\(-(-\frac{4}{3})\)، ثم نبسطه\(\frac{4}{3}\). وبالتالي، فإن المعكوس الجمعي لـ\(-\frac{4}{3}\) هو\(\frac{4}{3}\).
أوجد المعكوس الجمعي لـ
- \(\frac{7}{9}\)
- \(1.2\)
- \(-14\)
- \(-\frac{9}{4}\)
- إجابة
-
- \(-\frac{7}{9}\)
- \(-1.2\)
- \(14\)
- \(\frac{9}{4}\)
أوجد المعكوس الجمعي لـ
- \(\frac{7}{13}\)
- \(8.4\)
- \(-46\)
- \(-\frac{5}{2}\)
- إجابة
-
- \(-\frac{7}{13}\)
- \(-8.4\)
- \(46\)
- \(\frac{5}{2}\)
أوجد المعكوس الضربي لـ
- \(9\)
- \(-\frac{1}{9}\)
- \(0.9\)
- إجابة
-
لإيجاد المعكوس الضربي، نجد المقلوب.
- المعكوس الضربي لـ\(9\) هو مقلوب\(9\)، وهو\(\frac{1}{9}\). لذلك، فإن المعكوس الضربي لـ\(9\) is\(\frac{1}{9}\).
- المعكوس الضربي لـ\(-\frac{1}{9}\) هو مقلوب\(-\frac{1}{9}\)، وهو\(−9\). وبالتالي، فإن المعكوس الضربي لـ\(-\frac{1}{9}\) is\(-9\).
- لإيجاد المعكوس الضربي لـ\(0.9\)، نقوم أولاً بالتحويل\(0.9\) إلى كسر،\(\frac{9}{10}\). ثم نجد مقلوب الكسر. المعاملة بالمثل\(\frac{9}{10}\) هي\(\frac{10}{9}\). لذا فإن المعكوس الضربي لـ\(0.9\) هو\(\frac{10}{9}\).
أوجد المعكوس الضربي لـ
- \(4\)
- \(-\frac{1}{7}\)
- \(0.3\)
- إجابة
-
- \(\frac{1}{4}\)
- \(-7\)
- \(\frac{10}{3}\)
أوجد المعكوس الضربي لـ
- \(18\)
- \(-\frac{4}{5}\)
- \(0.6\)
- إجابة
-
- \(\frac{1}{18}\)
- \(-\frac{5}{4}\)
- \(\frac{5}{3}\)
استخدم خصائص الصفر
تقول خاصية الهوية الخاصة بالإضافة أنه عندما نضيف 0 إلى أي رقم، تكون النتيجة هي نفس الرقم. ماذا يحدث عندما نضرب عددًا في 0؟ الضرب في 0 يجعل المنتج يساوي صفرًا.
لأي رقم حقيقي a.
\[a \cdot 0 = 0 \quad 0 \cdot a = 0\]
منتج أي رقم حقيقي و 0 هو 0.
ماذا عن القسمة التي تتضمن الصفر؟ ما هي\(0\div 3\)؟ فكر في مثال حقيقي: إذا لم تكن هناك ملفات تعريف الارتباط في جرة ملفات تعريف الارتباط وكان على 3 أشخاص مشاركتها، فما عدد ملفات تعريف الارتباط التي يحصل عليها كل شخص؟ لا توجد ملفات تعريف ارتباط لمشاركتها، لذلك يحصل كل شخص على 0 ملفات تعريف الارتباط. لذا،
\[0\div 3 = 0\]
يمكننا التحقق من القسمة بحقيقة الضرب ذات الصلة.
\[12 \div 6 = 2 \text { because } 2 \cdot 6 = 12\]
لذلك نحن نعرف\(0\div 3=0\) ذلك بسبب\(0\cdot 3=0\).
لأي رقم حقيقي a، باستثناء\(0, \frac{0}{a}=0\) و\(0\div a=0\).
الصفر مقسومًا على أي رقم حقيقي باستثناء الصفر هو صفر.
الآن فكر في القسمة على الصفر. ما نتيجة قسمة 4 على 0؟ فكر في حقيقة الضرب ذات الصلة:\(4\div 0=?\) الوسائل\(?\cdot 0=4\). هل هناك رقم مضروبًا في 0 يعطي 4؟ نظرًا لأن أي رقم حقيقي مضروبًا في 0 يعطي 0، فلا يوجد رقم حقيقي يمكن ضربه في 0 للحصول على 4.
نستنتج أنه لا توجد إجابة لذلك نقول أن القسمة على 0 غير محددة.\(4\div 0\)
لأي رقم حقيقي a، باستثناء\(0, \frac{a}{0}\)\(a\div 0\) وغير معرف.
القسمة على الصفر غير محددة.
نحن نلخص خصائص الصفر أدناه.
الضرب بالصفر: لأي رقم حقيقي a،
\[a \cdot 0 = 0 \quad 0 \cdot a = 0 \quad \text { The product of any number and } 0 \text { is } 0\]
قسمة الصفر، القسمة على الصفر: لأي رقم حقيقي\(a, a\neq 0\)
\[\begin{array} { l l } { \frac { 0 } { a } = 0 } & { \text { Zero divided by any real number, except itself is zero. } } \\ { \frac { a } { 0 } \text { is undefined } } & { \text { Division by zero is undefined. } } \end{array}\]
قم بالتبسيط:
- \(-8\cdot 0\)
- \(\frac{0}{-2}\)
- \(\frac{-32}{0}\)
- إجابة
-
- \[\begin{array} { cc } { } &{-8\cdot 0}\\{\text{The product of any real number and 0 is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{0}{-2}}\\{\text{Zero divided by any real number, except}} &{} \\ {\text{itself, is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{-32}{0}}\\ {\text{Division by 0 is undefined.}} &{\text{undefined}} \end{array}\]
قم بالتبسيط:
- \(-14\cdot 0\)
- \(\frac{0}{-6}\)
- \(\frac{-2}{0}\)
- إجابة
-
- \(0\)
- \(0\)
- غير محدد
قم بالتبسيط:
- \(0(-17)\)
- \(\frac{0}{-10}\)
- \(\frac{-5}{0}\)
- إجابة
-
- \(0\)
- \(0\)
- غير محدد
سنتدرب الآن على استخدام خصائص الهويات والمعكوسات والصفر لتبسيط التعبيرات.
قم بالتبسيط:
- \(\frac{0}{n + 5}\)، أين\(n\neq −5\)
- \(\frac{10 - 3p}{0}\)أين\(10 - 3p \neq 0\)
- إجابة
-
- \[\begin{array} { ll } { } &{\frac{0}{n + 5}}\\ {\text { Zero divided by any real number except }} &{0} \\ { \text { itself is } 0.} &{} \end{array}\]
- \[\begin{array} { ll } { } &{\frac{10 - 3p}{0}}\\ {\text { Division by 0 is undefined }} &{\text{undefined}} \end{array}\]
قم بالتبسيط:\(−84n+(−73n)+84n\).
- إجابة
-
\[\begin{array} { l l } { } &{−84n+(−73n)+84n} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { opposites; use the commutative property of } } &{- 84 n + 84 n + ( - 73 n ) } \\ { \text { addition to re-order the terms. } } &{} \\ \\ { \text { Add left to right. } } &{0 + (-73)}\\ \\{ \text { Add. } } &{-73n} \end{array}\]
قم بالتبسيط:\(−27a+(−48a)+27a\).
- إجابة
-
\(−48a\)
قم بالتبسيط:\(39x+(−92x)+(−39x)\).
- إجابة
-
\(−92x\)
سنرى الآن كيف أن التعرف على المعاملة بالمثل مفيد. قبل الضرب من اليسار إلى اليمين، ابحث عن الترددية - منتجها هو 1.
قم بالتبسيط:\(\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}\)
- إجابة
-
\[\begin{array} { l l } { } &{\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { reciprocals, so use the commutative } } &{\frac{7}{15}\cdot\frac{15}{7}\cdot\frac{8}{23}} \\ { \text { property of multiplication to re-order the } } &{} \\ { \text { factors. } } &{}\\ \\{ \text { Multiply left to right. } } &{1\cdot\frac{8}{23}} \\\\{\text{Multiply.}} &{\frac{8}{23}}\end{array}\]
قم بالتبسيط:\(\frac{9}{16}\cdot\frac{5}{49}\cdot\frac{16}{9}\)
- إجابة
-
\(\frac{5}{49}\)
قم بالتبسيط:\(\frac{6}{17}\cdot\frac{11}{25}\cdot\frac{17}{6}\)
- إجابة
-
\(\frac{11}{25}\)
قم بالتبسيط:
- \(\frac{0}{m + 7}\)، أين\(m \neq -7\)
- \(\frac{18 - 6c}{0}\)، أين\(18 - 6c \neq 0\)
- إجابة
-
- 0
- غير محدد
قم بالتبسيط:
- \(\frac{0}{d - 4}\)، أين\(d \neq 4\)
- \(\frac{15 - 4q}{0}\)، أين\(15 - 4q \neq 0\)
- إجابة
-
- 0
- غير محدد
قم بالتبسيط:\(\frac{3}{4}\cdot\frac{4}{3}(6x + 12)\)
- إجابة
-
\[\begin{array} { l l } { } &{\frac{3}{4}\cdot\frac{4}{3}(6x + 12)} \\ { \text { There is nothing to do in the parentheses, } } &{}\\ { \text { so multiply the two fractions first—notice, } } &{1(6x + 12)} \\ { \text { they are reciprocals. } } &{} \\ \\{ \text { Simplify by recognizing the multiplicative } } &{} \\{\text{ identity.}} &{6x + 12} \end{array}\]
قم بالتبسيط:\(\frac{2}{5}\cdot\frac{5}{2}(20y + 50)\)
- إجابة
-
\(20y + 50\)
قم بالتبسيط:\(\frac{3}{8}\cdot\frac{8}{3}(12z + 16)\)
- إجابة
-
\(12z + 16\)
تبسيط التعبيرات باستخدام خاصية التوزيع
لنفترض أن ثلاثة أصدقاء سيذهبون إلى السينما. يحتاج كل منهم إلى 9.25 دولارًا - أي 9 دولارات وربع واحد - لدفع ثمن تذاكرهم. كم من المال يحتاجون إليه جميعًا معًا؟
يمكنك التفكير في الدولارات بشكل منفصل عن الأرباع. إنهم بحاجة إلى 3 أضعاف 9 دولارات، أي 27 دولارًا، و 3 مرات في الربع الأول، أي 75 سنتًا. في المجموع، يحتاجون إلى 27.75 دولارًا. إذا فكرت في إجراء الرياضيات بهذه الطريقة، فأنت تستخدم خاصية التوزيع.
\[\begin{array} { rr } {\text { If } a , b , c \text { are real numbers, then }} &{a ( b + c ) = a b + a c} \\ \\{ \text { Also,} } &{( b + c ) a = b a + c a} \\ {} &{a ( b - c ) = a b - a c } &{} \\{} &{( b - c ) a = b a - c a } \end{array}\]
بالعودة إلى أصدقائنا في الأفلام، يمكننا العثور على المبلغ الإجمالي للأموال التي يحتاجونها على النحو التالي:
\[\begin{array} { c } { 3 ( 9.25 ) } \\ { 3 ( 9 + 0.25 ) } \\ { 3 ( 9 ) + 3 ( 0.25 ) } \\ { 27 + 0.75 } \\ \\ { 27.75 } \end{array}\]
في الجبر، نستخدم خاصية التوزيع لإزالة الأقواس أثناء تبسيط التعبيرات.
على سبيل المثال، إذا طُلب منا تبسيط التعبير\(3(x+4)\)، فإن ترتيب العمليات ينص على العمل بين قوسين أولاً. ولكن لا يمكننا إضافة x و 4، لأنها ليست مثل المصطلحات. لذلك نستخدم خاصية التوزيع، كما هو موضح في التمرين\(\PageIndex{31}\).
قم بالتبسيط:\(3(x+4)\).
- إجابة
-
\[\begin{array} { l l } { } & { 3 ( x + 4 ) } \\ { \text { Distribute. } } & { 3 \cdot x + 3 \cdot 4 } \\ { \text { Multiply. } } & { 3 x + 12 } \end{array}\]
قم بالتبسيط:\(4(x+2)\).
- إجابة
-
\(4x + 8\)
قم بالتبسيط:\(6(x+7)\).
- إجابة
-
\(6x + 42\)
يجد بعض الطلاب أنه من المفيد رسم الأسهم لتذكيرهم بكيفية استخدام خاصية التوزيع. ثم\(\PageIndex{31}\) ستبدو الخطوة الأولى في التمرين كما يلي:
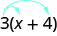
قم بالتبسيط:\(8(\frac{3}{8}x+\frac{1}{4})\).
- إجابة
-
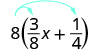
قم بالتوزيع. 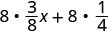
اضرب. 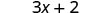
قم بالتبسيط:\(6(\frac{5}{6}y+\frac{1}{2})\).
- إجابة
-
\(5y + 3\)
قم بالتبسيط:\(12(\frac{1}{3}n+\frac{3}{4})\).
- إجابة
-
\(4n + 9\)
\(\PageIndex{37}\)سيكون استخدام خاصية التوزيع كما هو موضح في التمرين مفيدًا جدًا عندما نحل تطبيقات النقود في الفصول اللاحقة.
قم بالتبسيط:\(100(0.3+0.25q)\).
- إجابة
-
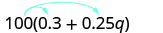
قم بالتوزيع. 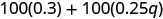
اضرب. 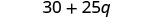
قم بالتبسيط:\(100(0.7+0.15p)\).
- إجابة
-
\(70 + 15p\)
قم بالتبسيط:\(100(0.04+0.35d)\).
- إجابة
-
\(4 + 35d\)
عندما نوزع رقمًا سالبًا، نحتاج إلى توخي الحذر الشديد لتصحيح العلامات!
قم بالتبسيط:\(−2(4y+1)\).
- إجابة
-
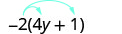
قم بالتوزيع. 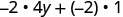
اضرب. 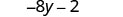
قم بالتبسيط:\(−3(6m+5)\).
- إجابة
-
\(−18m-15)\)
قم بالتبسيط:\(−6(8n+11)\).
- إجابة
-
\(−48n- 66)\)
قم بالتبسيط:\(−11(4-3a)\).
- إجابة
-
قم بالتوزيع. 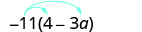
اضرب. 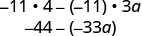
قم بالتبسيط. 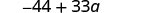
لاحظ أنه يمكنك أيضًا كتابة النتيجة كـ\(33a−44\). هل تعرف لماذا؟
قم بالتبسيط:\(−5(2-3a)\).
- إجابة
-
\(10+ 15a\)
قم بالتبسيط:\(−7(8-15y)\).
- إجابة
-
\(-56 + 105y\)
\(\PageIndex{46}\)سيوضح التمرين كيفية استخدام خاصية التوزيع للعثور على عكس التعبير.
قم بالتبسيط:\(−(y+5)\).
- إجابة
-
\[\begin{array} { ll } {} &{-(y + 5)} \\ \\{ \text {Multiplying by -1 results in the opposite.} } &{-1( y + 5 )} \\ \\ {\text{Distribute.}} &{-1\cdot y + (-1)\cdot 5}\\ \\{\text{Simplify.}} &{-y + (-5)} \\ \\ {} &{-y - 5} \end{array}\]
قم بالتبسيط:\(−(z-11)\).
- إجابة
-
\(-z + 11\)
قم بالتبسيط:\(−(x -4)\).
- إجابة
-
\(-x + 4\)
ستكون هناك أوقات سنحتاج فيها إلى استخدام خاصية التوزيع كجزء من ترتيب العمليات. ابدأ بالنظر إلى الأقواس. إذا تعذر تبسيط التعبير الموجود داخل الأقواس، فستكون الخطوة التالية هي الضرب باستخدام خاصية التوزيع، التي تزيل الأقواس. سيوضح المثالان التاليان هذا.
قم بالتبسيط:\(8−2(x + 3)\).
تأكد من اتباع ترتيب العمليات. يأتي الضرب قبل الطرح، لذلك سنقوم بتوزيع 2 أولاً ثم الطرح.
- إجابة
-
\[\begin{array} { ll } {} &{8−2(x + 3)} \\ \\{ \text {Distribute.} } &{8−2\cdot x -2\cdot 3} \\ \\ {\text{Multiply.}} &{8 - 2x - 6}\\ \\{\text{Combine like terms.}} &{-2x + 2} \end{array}\]
قم بالتبسيط:\(9−3(x + 2)\).
- إجابة
-
\(3 - 3x\)
قم بالتبسيط:\(7x−5(x + 4)\).
- إجابة
-
\(2x - 20\)
قم بالتبسيط:\(4(x - 8)−(x + 3)\).
- إجابة
-
\[\begin{array} { ll } {} &{4(x - 8)−(x + 3)} \\ \\{ \text {Distribute.} } &{4x - 32 - x - 3} \\ \\{\text{Combine like terms.}} &{3x - 35} \end{array}\]
قم بالتبسيط:\(6(x - 9)−(x + 12)\).
- إجابة
-
\(5x - 66\)
قم بالتبسيط:\(8(x - 1)-(x + 5)\).
- إجابة
-
\(7x - 13\)
تم تلخيص جميع خصائص الأرقام الحقيقية التي استخدمناها في هذا الفصل في الجدول\(\PageIndex{1}\).
| الملكية التبادلية | |
| من الجمع إذا كانت a و b أرقامًا حقيقية، ثم الضرب إذا كانت a و b أرقامًا حقيقية، إذن |
\(a+b=b+a\) \(a\cdot b=b\cdot a\) |
| الملكية الترابطية | |
| من الجمع إذا كانت a و b و c أرقامًا حقيقية، ثم الضرب إذا كانت a و b و c أرقامًا حقيقية، إذن |
\((a+b)+c=a+(b+c)\) \((a\cdot b)\cdot c=a\cdot (b\cdot c)\) |
| خاصية التوزيع | |
| إذا كانت a، b، c هي أرقام حقيقية، إذن | \(a(b+c)=ab+ac\) |
| خاصية الهوية | |
|
إضافة: بالنسبة لأي رقم حقيقي a: الضرب لأي رقم حقيقي a: |
\(a+0=a\) \(0+a=a\) \(1·a=a\) |
| خاصية عكسية | |
| الجمع: بالنسبة لأي رقم حقيقي، أ، \(−a\) هو المعكوس الجمعي لـ a من الضرب لأي رقم حقيقي\(a,a\neq 0\) \(\frac{1}{a}\) هو معكوس ضربي لـ |
\(a+(−a)=0\) \(a\cdot\frac{1}{a}=1\) |
| خصائص الصفر | |
|
لأي رقم حقيقي a، لأي رقم حقيقي\(a,a\neq 0\) |
\(a\cdot 0=0\) \(0\cdot a=0\) \(\frac{0}{a} = 0\) |
المفاهيم الرئيسية
- الملكية التبادلية لـ
- إضافة: إذا كانت a و b أرقامًا حقيقية، إذن\(a+b=b+a\).
- الضرب: إذا كانت a و b أرقامًا حقيقية، إذن\(a\cdot b=b\cdot a\). عند الإضافة أو الضرب، فإن تغيير الترتيب يعطي نفس النتيجة.
- الملكية الترابطية لـ
- الإضافة: إذا كانت a و b و c أرقامًا حقيقية، إذن\((a+b)+c=a+(b+c)\).
- الضرب: إذا كانت a و b و c أرقامًا حقيقية، إذن\((a\cdot b)\cdot c=a\cdot (b\cdot c)\).
عند الإضافة أو الضرب، فإن تغيير التجميع يعطي نفس النتيجة.
- خاصية التوزيع: إذا كانت a و b و c أرقامًا حقيقية، إذن
- \(a(b+c)=ab+ac\)
- \((b+c)a=ba+ca\)
- \(a(b-c)=ab-ac\)
- \((b+c)a=ba-ca\)
- خاصية الهوية
- من الإضافة: لأي رقم حقيقي a:\(a+0=a\)
0 هي الهوية المضافة - من الضرب: لأي رقم حقيقي a:\(a\cdot 1=a \quad 1·a=a\)
1 1 هي الهوية المضاعفة
- من الإضافة: لأي رقم حقيقي a:\(a+0=a\)
- خاصية عكسية
- من الإضافة: لأي رقم حقيقي\(a, a+(−a)=0\). الرقم ونقيضه يضيفان إلى الصفر. \(−a\)هو المعكوس الجمعي لـ a.
- من الضرب: لأي رقم حقيقي\(a,(a\neq 0)a\cdot\frac{1}{a}=1\). عدد ومقتضبيه في واحد. \(\frac{1}{a}\)هو المعكوس الضربي لـ a.
- خصائص الصفر
- لأي رقم حقيقي a،
\(a\cdot 0=0 \quad 0·a=0\) - منتج أي رقم حقيقي و 0 هو 0. - \(\frac{0}{a}=0\)لـ\(a\neq 0\) - صفر مقسومًا على أي رقم حقيقي باستثناء الصفر هو صفر.
- \(\frac{a}{0}\)غير محدد - القسمة على الصفر غير محددة.
- لأي رقم حقيقي a،


