Skip to main content
Global

1.9: الأرقام الحقيقية

  1. Last updated
  2. Save as PDF
  • Page ID
    200658

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • تبسيط التعبيرات باستخدام الجذور التربيعية
    • حدد الأعداد الصحيحة والأرقام العقلانية والأرقام غير المنطقية والأرقام الحقيقية
    • حدد موقع الكسور على خط الأعداد
    • حدد موقع الأرقام العشرية على خط الأرقام
    ملاحظة

    يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي تم تناولها في هذا القسم في فصول الجبر المسبق والأرقام العشرية وخصائص الأعداد الحقيقية.

    تبسيط التعبيرات باستخدام الجذور التربيعية

    تذكر أنه عندما\(n\) يتم ضرب الرقم في حد ذاته، فإننا\(n^{2}\) نكتبه ونقرأه «\(n\)مربعًا». النتيجة تسمى مربع\(n\). على سبيل المثال،

    \[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

    وبالمثل، 121 هو مربع 11، لأنه\(11^{2}\) 121.

    مربع الرقم

    إذا كان\(n^{2}=m\)، إذن\(m\) هو مربع\(n\).

    ملاحظة

    سيساعدك القيام بنشاط الرياضيات المتلاعبة «الأرقام المربعة» على تطوير فهم أفضل للأرقام المربعة المثالية.

    أكمل الجدول التالي لتوضيح مربعات أعداد العد من 1 إلى 15.

    يوجد جدول يحتوي على صفين و 17 عمودًا. يقرأ الصف الأول من اليسار إلى اليمين الأرقام، n، 1، 2، 3، 4، 5، 6، 7، 8، 9، 10، 11، 12، 13، 14، 15. يُقرأ الصف الثاني من اليسار إلى اليمين مربع، n مربع، فارغ، فارغ، فارغ، فارغ، فارغ، فارغ، فارغ، 64، فارغ، فارغ، فارغ، 121، فارغ، فارغ، فارغ، فارغ، فارغ.
    الشكل\(\PageIndex{1}\)

    تسمى الأرقام الموجودة في الصف الثاني بالأرقام المربعة المثالية. سيكون من المفيد تعلم التعرف على الأرقام المربعة المثالية.

    مربعات أرقام العد هي أرقام موجبة. ماذا عن مربعات الأرقام السالبة؟ نحن نعلم أنه عندما تكون علامات الرقمين متماثلة، يكون منتجهما إيجابيًا. لذا فإن مربع أي رقم سالب يكون موجبًا أيضًا.

    \[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

    هل لاحظت أن هذه المربعات هي نفس مربعات الأرقام الموجبة؟

    في بعض الأحيان سنحتاج إلى النظر إلى العلاقة بين الأرقام ومربعاتها في الاتجاه المعاكس. لأننا\(10^{2}=100\) نقول أن 100 هو مربع 10. نقول أيضًا أن 10 هو الجذر التربيعي لـ 100. يُطلق على الرقم الذي يكون مربعه مم اسم الجذر التربيعي لـ\(m\).

    الجذر التربيعي لعدد

    إذا كان\(n^{2}=m\)، إذن\(n\) هو الجذر التربيعي لـ\(m\).

    لاحظ\((−10)^{2}=100\) أيضًا\(−10\) أن الجذر التربيعي لـ\(100\). لذلك،\(−10\) كلاهما\(10\) لهما جذور مربعة لـ\(100\).

    لذلك، كل عدد موجب له جذران مربعان - أحدهما موجب والآخر سالب. ماذا لو أردنا فقط الجذر التربيعي الموجب لعدد موجب؟ تشير العلامة الراديكالية إلى الجذر التربيعي الإيجابي.\(\sqrt{m}\) يسمى الجذر التربيعي الموجب بالجذر التربيعي الرئيسي. عندما نستخدم العلامة الجذرية فهذا يعني دائمًا أننا نريد الجذر التربيعي الرئيسي.

    نستخدم أيضًا العلامة الجذرية للجذر التربيعي للصفر. بسبب\(0^{2}=0, \sqrt{0}=0\). لاحظ أن الصفر يحتوي على جذر مربع واحد فقط.

    تدوين الجذر التربيعي

    \(\sqrt{m}\)يُقرأ «الجذر التربيعي لـ\(m\)»

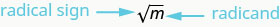
    يتم إعطاء الجذر التربيعي، مع وجود سهم للإشارة الجذرية (يبدو وكأنه علامة اختيار بخط أفقي يمتد من نهايتها الطويلة) للإشارة الجذرية وسهم إلى الرقم الموجود أسفل العلامة الجذرية، والتي تم وضع علامة راديكاند عليها.

    إذا\(m = n^{2}\)، إذن\(\sqrt{m} = n\)، من أجل\(n\geq 0\).

    الجذر التربيعي لـ\(m\),\(\sqrt{m}\), هو الرقم الموجب الذي يكون مربعه\(m\).

    بما أن 10 هو الجذر التربيعي الرئيسي لـ 100، فإننا نكتب\(\sqrt{100}=10\). قد ترغب في إكمال الجدول التالي لمساعدتك في التعرف على الجذور التربيعية.

    يوجد جدول يحتوي على صفين و 15 عمودًا. يقرأ الصف الأول من الجذر التربيعي الأيسر إلى الأيمن لـ 1، والجذر التربيعي لـ 4، والجذر التربيعي لـ 9، والجذر التربيعي لـ 16، والجذر التربيعي لـ 25، والجذر التربيعي لـ 36، والجذر التربيعي لـ 64، والجذر التربيعي لـ 81، والجذر التربيعي لـ 121، والجذر التربيعي لـ 144، والجذر التربيعي لـ 169، والجذر التربيعي لـ 196، الجذر التربيعي لـ 225. يتكون الصف الثاني من جميع الفراغات باستثناء الخلية العاشرة تحت الجذر التربيعي لـ 100، والتي تقرأ 10.
    الشكل\(\PageIndex{2}\)
    التمارين\(\PageIndex{1}\)

    قم بالتبسيط:

    1. \(\sqrt{25}\)
    2. \(\sqrt{121}\)
    إجابة
    1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
    2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
    التمارين\(\PageIndex{2}\)

    قم بالتبسيط:

    1. \(\sqrt{36}\)
    2. \(\sqrt{169}\)
    إجابة
    1. 6
    2. 13
    التمارين\(\PageIndex{3}\)

    قم بالتبسيط:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    إجابة
    1. 4
    2. 14

    نحن نعلم أن كل رقم موجب له جذران تربيعيان وأن العلامة الجذرية تشير إلى الموجب. نحن نكتب\(\sqrt{100)=10\). إذا أردنا إيجاد الجذر التربيعي السالب لعدد ما، فإننا نضع القيمة السالبة أمام العلامة الجذرية. على سبيل المثال،\(-\sqrt{100)=-10\). نقرأ على\(-\sqrt{100)\) أنه «عكس الجذر التربيعي لـ 10".

    التمارين\(\PageIndex{4}\)

    قم بالتبسيط:

    1. \(-\sqrt{9}\)
    2. \(-\sqrt{144}\)
    إجابة
    1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
    2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
    التمارين\(\PageIndex{5}\)

    قم بالتبسيط:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    إجابة
    1. −2
    2. −15
    التمارين\(\PageIndex{6}\)

    قم بالتبسيط:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    إجابة
    1. −9
    2. −10

    تحديد الأعداد الصحيحة والأعداد النسبية والأعداد غير النسبية والأعداد الحقيقية

    لقد وصفنا بالفعل الأرقام على أنها عد الأرقام s والأرقام الصحيحة s والأعداد الصحيحة. ما الفرق بين هذه الأنواع من الأرقام؟

    \[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

    ما نوع الأرقام التي سنحصل عليها إذا بدأنا بجميع الأعداد الصحيحة ثم أدرجنا جميع الكسور؟ تشكل الأرقام التي سنحصل عليها مجموعة الأرقام العقلانية. الرقم العقلاني هو رقم يمكن كتابته كنسبة من عددين صحيحين.

    رقم عقلاني

    الرقم العقلاني هو رقم النموذج\(\dfrac{p}{q}\)، حيث p و q عبارة عن أعداد صحيحة و\(q \neq 0\)

    يمكن كتابة الرقم العقلاني كنسبة عددين صحيحين.

    جميع الكسور الموقعة، مثل\(\dfrac{4}{5}\)،\(-\dfrac{7}{8}\)،\(\dfrac{13}{4}\)،\(-\dfrac{20}{3}\) هي أرقام منطقية. كل عداد وكل قاسم هو عدد صحيح.

    هل الأعداد الصحيحة أرقام عقلانية؟ لتحديد ما إذا كان العدد الصحيح هو رقم منطقي، نحاول كتابته كنسبة من عددين صحيحين. يمكن كتابة كل عدد صحيح كنسبة من الأعداد الصحيحة بعدة طرق. على سبيل المثال، 3 يعادل\(\dfrac{3}{1}\)\(-\dfrac{6}{2}\)،\(\dfrac{9}{3}\)،\(\dfrac{12}{4}\)،\(-\dfrac{15}{5} \ldots\)

    طريقة سهلة لكتابة عدد صحيح كنسبة من الأعداد الصحيحة هي كتابته ككسر بمقامه واحد.

    \[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

    نظرًا لأنه يمكن كتابة أي عدد صحيح كنسبة من عددين صحيحين، فإن جميع الأعداد الصحيحة هي أرقام منطقية! تذكر أن أرقام العد والأرقام الصحيحة هي أيضًا أعداد صحيحة، وبالتالي فهي منطقية أيضًا.

    ماذا عن الأرقام العشرية؟ هل هم عقلانيون؟ دعونا نلقي نظرة على بعضها لمعرفة ما إذا كان بإمكاننا كتابة كل منها كنسبة من عددين صحيحين.

    لقد رأينا بالفعل أن الأعداد الصحيحة هي أرقام عقلانية. \(−8\)يمكن كتابة العدد الصحيح على هيئة عدد عشري\(−8.0\). لذلك، من الواضح أن بعض الأرقام العشرية منطقية.

    فكر في الرقم العشري\(7.3\). هل يمكننا كتابتها كنسبة من عددين صحيحين؟ لأنه\(7.3\) يعني أنه\(7\dfrac{3}{10}\) يمكننا كتابته ككسر غير صحيح،\(\dfrac{73}{10}\). هكذا\(7.3\) هي نسبة الأعداد الصحيحة\(73\) و\(10\). إنه رقم عقلاني.

    بشكل عام، أي رقم عشري ينتهي بعد عدد من الأرقام (مثل\(7.3\) أو\(−1.2684\)) هو رقم منطقي. يمكننا استخدام القيمة المكانية للرقم الأخير كمقام عند كتابة العدد العشري في صورة كسر.

    التمارين\(\PageIndex{7}\)

    اكتب كنسبة من عددين صحيحين:

    1. −27
    2. 7.31
    إجابة
    1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
    2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

    لذلك نرى أن −27 و7.31 كلاهما عددان منطقيان، حيث يمكن كتابتهما كنسبة من عددين صحيحين.

    التمارين\(\PageIndex{8}\)

    اكتب كنسبة من عددين صحيحين:

    1. −24
    2. 3.57
    إجابة
    1. \(\dfrac{-24}{1}\)
    2. \(\dfrac{357}{100}\)
    التمارين\(\PageIndex{9}\)

    اكتب كنسبة من عددين صحيحين:

    1. −19
    2. 8.41
    إجابة
    1. \(\dfrac{-19}{1}\)
    2. \(\dfrac{841}{100}\)
    دعونا ننظر إلى الشكل العشري للأرقام التي نعرف أنها منطقية.

    لقد رأينا أن كل عدد صحيح هو رقم منطقي، لأنه\(a = \dfrac{a}{1}\) بالنسبة لأي عدد صحيح،\(a\). يمكننا أيضًا تغيير أي عدد صحيح إلى رقم عشري بإضافة نقطة عشرية وصفر.

    \[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

    لقد رأينا أيضًا أن كل كسر هو رقم منطقي. انظر إلى الشكل العشري للكسور التي اعتبرناها أعلاه.

    \[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

    ماذا تخبرنا هذه الأمثلة؟

    يمكن كتابة كل رقم منطقي كنسبة من الأعداد الصحيحة، (\(\dfrac{p}{q}\)، حيث p و q عبارة عن أعداد صحيحة و\(q\neq 0\))، وكرقم عشري يتوقف أو يتكرر.

    فيما يلي الأرقام التي نظرنا إليها أعلاه معبرًا عنها كنسبة من الأعداد الصحيحة وكعدد عشري:

    الكسور الأعداد الصحيحة
    رقم \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) −2 −1 0 1 2 3
    نسبة الأعداد الصحيحة \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) \(-\frac{2}{1}\) \(-\frac{1}{1}\) \(\frac{0}{1}\) \(\frac{1}{1}\) \(\frac{2}{1}\) \(\frac{3}{1}\)
    نموذج عشري 0.8 −0.875 3.25 \(−6.\overline{6}\) −2.0 −1.0 0.0 1.0 2.0 3.0
    طاولة\(\PageIndex{1}\)
    رقم عقلاني

    الرقم العقلاني هو رقم النموذج\(\frac{p}{q}\)، حيث p و q عبارة عن أعداد صحيحة و\(q\neq 0\)

    يتوقف النموذج العشري الخاص به أو يتكرر.

    هل هناك أي أرقام عشرية لا تتوقف أو تتكرر؟ نعم!

    الرقم\(\pi\) (الحرف اليوناني pi، يُنطق «pie»)، وهو مهم جدًا في وصف الدوائر، له شكل عشري لا يتوقف أو يتكرر.

    \[\pi =3.141592654\ldots\]

    يمكننا أيضًا إنشاء نمط عشري لا يتوقف أو يتكرر، مثل

    \[2.01001000100001\ldots\]

    لا يمكن كتابة الأرقام التي لا يتوقف شكلها العشري أو يتكرر ككسر من الأعداد الصحيحة. نسمي هذه الأرقام غير منطقية.

    رقم غير منطقي

    الرقم غير العقلاني هو رقم لا يمكن كتابته كنسبة من عددين صحيحين.

    لا يتوقف شكله العشري ولا يتكرر.

    دعونا نلخص طريقة يمكننا استخدامها لتحديد ما إذا كان الرقم عقلانيًا أم غير منطقي.

    عقلاني أو غير عقلاني؟

    إذا كان الشكل العشري للرقم

    • يتكرر أو يتوقف، الرقم عقلاني.
    • لا يتكرر ولا يتوقف، الرقم غير منطقي.
    التمارين\(\PageIndex{10}\)

    بالنظر إلى\(0.58\overline{3}, 0.47, 3.605551275\ldots\) قائمة الأرقام

    1. أرقام عقلانية
    2. أرقام غير منطقية.
    إجابة
    1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
    2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
    التمارين\(\PageIndex{11}\)

    للحصول على قائمة الأرقام المعطاة

    1. أرقام عقلانية
    2. أرقام غير منطقية:\(0.29, 0.81\overline{6}, 2.515115111….\)
    إجابة
    1. \(0.29, 0.81\overline{6}\)
    2. \(2.515115111….\)
    التمارين\(\PageIndex{12}\)

    للحصول على قائمة الأرقام المعطاة

    1. أرقام عقلانية
    2. أرقام غير منطقية:\(2.6\overline{3}, 0.125, 0.418302…\)
    إجابة
    1. \(2.6\overline{3}, 0.125\)
    2. \(0.418302…\)
    التمارين\(\PageIndex{13}\)

    بالنسبة لكل رقم معطى، حدد ما إذا كان عقلانيًا أم غير منطقي:

    1. \(\sqrt{36}\)
    2. \(\sqrt{44}\)
    إجابة
    1. اعلم أن 36 هو مربع مثالي، منذ ذلك الحين\(6^{2} = 36\). لذلك\(\sqrt{36} = 6\)،\(\sqrt{36}\) فمن المنطقي.
    2. تذكر\(6^{2} = 36\) ذلك\(7^{2} = 49\)،\(44\) وكذلك ليس مربعًا مثاليًا. لذلك، لن يتكرر الشكل العشري أبدًا\(\sqrt{44}\) ولن يتوقف أبدًا، لذلك\(\sqrt{44}\) فهو غير منطقي.
    التمارين\(\PageIndex{14}\)

    بالنسبة لكل رقم معطى، حدد ما إذا كان عقلانيًا أم غير منطقي:

    1. \(\sqrt{81}\)
    2. \(\sqrt{17}\)
    إجابة
    1. معقول
    2. غير منطقي
    التمارين\(\PageIndex{15}\)

    بالنسبة لكل رقم معطى، حدد ما إذا كان عقلانيًا أم غير منطقي:

    1. \(\sqrt{116}\)
    2. \(\sqrt{121}\)
    إجابة
    1. غير منطقي
    2. معقول

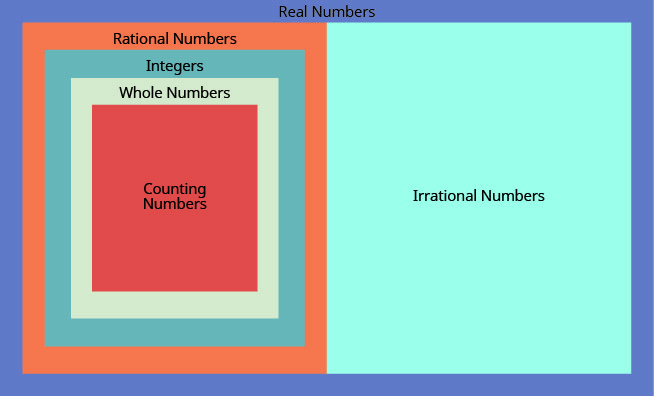
    لقد رأينا أن جميع أرقام العد هي أعداد صحيحة، وجميع الأرقام الصحيحة هي أعداد صحيحة، وجميع الأعداد الصحيحة هي أرقام عقلانية. الأرقام غير المنطقية هي الأرقام التي لا يتوقف شكلها العشري ولا يتكرر. عندما نجمع الأعداد النسبية والأرقام غير المنطقية، نحصل على مجموعة الأعداد الحقيقية s.

    الرقم الحقيقي

    الرقم الحقيقي هو رقم عقلاني أو غير منطقي.

    جميع الأرقام التي نستخدمها في الجبر الأولي هي أرقام حقيقية. \(\PageIndex{3}\)يوضح الشكل كيفية توافق مجموعات الأرقام التي ناقشناها في هذا القسم معًا.

    يتكون هذا الشكل من مخطط Venn. للبدء، يوجد مستطيل كبير يحمل علامة الأرقام الحقيقية. يتكون النصف الأيمن من المستطيل من الأرقام غير النسبية. يتكون النصف الأيسر من الأرقام النسبية. داخل مستطيل الأرقام النسبية، توجد أعداد صحيحة...، سالب 2، سالب 1، 0، 1، 2،... داخل مستطيل الأعداد الصحيحة، توجد أعداد صحيحة 0، 1، 2، 3،... داخل مستطيل الأعداد الصحيحة، هناك عد الأعداد 1، 2، 3،...
    الشكل\(\PageIndex{3}\): يعرض هذا المخطط مجموعات الأرقام التي تشكل مجموعة الأرقام الحقيقية. هل يبدو مصطلح «الأرقام الحقيقية» غريبًا بالنسبة لك؟ هل هناك أي أرقام غير «حقيقية»، وإذا كان الأمر كذلك، فماذا يمكن أن تكون؟

    هل يمكننا التبسيط\(\sqrt{-25}\)؟ هل هناك رقم مربعه\(−25\)؟

    \[(\quad)^{2}=−25?\]

    لا يحتوي أي من الأرقام التي تعاملنا معها حتى الآن على مربع\(−25\). لماذا؟ أي رقم موجب مربع يكون موجبًا. أي رقم سالب مربّع يكون موجبًا. لذلك نقول أنه لا يوجد رقم حقيقي يساوي\(\sqrt{-25}\).

    الجذر التربيعي للرقم السالب ليس رقمًا حقيقيًا.

    التمارين\(\PageIndex{16}\)

    بالنسبة لكل رقم معطى، حدد ما إذا كان رقمًا حقيقيًا أم لا:

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{64}\)
    إجابة
    1. لا يوجد رقم حقيقي مربعه\(−169\). لذلك،\(\sqrt{-169}\) ليس رقمًا حقيقيًا.
    2. بما أن السالب أمام الراديكالي، أي\(−8\)،\(-\sqrt{64}\) بما أن الرقم الحقيقي\(−8\) هو رقم حقيقي،\(-\sqrt{64}\) فهو رقم حقيقي.
    التمارين\(\PageIndex{17}\)

    بالنسبة لكل رقم معطى، حدد ما إذا كان رقمًا حقيقيًا أم لا:

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{81}\)
    إجابة
    1. ليس رقمًا حقيقيًا
    2. رقم حقيقي
    التمارين\(\PageIndex{18}\)

    بالنسبة لكل رقم معطى، حدد ما إذا كان رقمًا حقيقيًا أم لا:

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    إجابة
    1. رقم حقيقي
    2. ليس رقمًا حقيقيًا
    التمارين\(\PageIndex{19}\)

    بالنظر إلى الأرقام\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\)، ضع قائمة بـ

    1. أرقام صحيحة
    2. الأعداد الصحيحة
    3. أرقام عقلانية
    4. أرقام غير منطقية
    5. أرقام حقيقية
    إجابة
    1. تذكر أن الأعداد الصحيحة هي 0، 1، 2، 3،... و8 هو العدد الصحيح الوحيد المعطى.
    2. الأعداد الصحيحة هي الأعداد الصحيحة، أضدادها، و 0. لذا فإن العدد الكامل 8 هو عدد صحيح، و−7 هو عكس عدد صحيح، لذا فهو عدد صحيح أيضًا. لاحظ أيضًا أن 64 هو مربع 8 إذن\(-\sqrt{64} = -8\). لذا فإن الأعداد الصحيحة هي\(−7, 8, \sqrt{64}\).
    3. نظرًا لأن جميع الأعداد الصحيحة عقلانية،\(-7, 8, -\sqrt{64}\) فهي عقلانية. تتضمن الأرقام العقلانية أيضًا الكسور والأرقام العشرية التي تتكرر أو تتوقف،\(\frac{14}{5}\) وهكذا\(5.9\) تكون منطقية. لذا فإن قائمة الأرقام العقلانية هي\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
    4. تذكر أن الرقم 5 ليس مربعًا مثاليًا، لذا فهو\(\sqrt{5}\) أمر غير منطقي.
    5. جميع الأرقام المدرجة هي أرقام حقيقية.
    التمارين\(\PageIndex{20}\)

    بالنسبة للأرقام المعطاة، قم بإدراج

    1. أرقام صحيحة
    2. الأعداد الصحيحة
    3. أرقام عقلانية
    4. أرقام غير منطقية
    5. الأرقام الحقيقية:\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    إجابة
    1. \(4, \sqrt{49}\).
    2. \(−3, 4, \sqrt{49}\)
    3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    4. \( -\sqrt{2}\)
    5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    التمارين\(\PageIndex{21}\)

    بالنسبة للأرقام المعطاة، قم بإدراج

    1. أرقام صحيحة
    2. الأعداد الصحيحة
    3. أرقام عقلانية
    4. أرقام غير منطقية
    5. الأرقام الحقيقية:\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
    إجابة
    1. \(6, \sqrt{121}\).
    2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
    3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
    4. \(2.041975…\)
    5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

    حدد موقع الكسور على خط الأعداد

    في المرة الأخيرة التي نظرنا فيها إلى خط الأعداد، كان عليه فقط أعداد صحيحة موجبة وسالبة. نريد الآن تضمين الكسور s والأرقام العشرية عليها.

    ملاحظة

    سيساعدك القيام بنشاط الرياضيات المتلاعبة «خط الأرقام الجزء 3" على تطوير فهم أفضل لموقع الكسور على خط الأعداد.

    لنبدأ بالكسور وتحديد الموقع\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\)\(\frac{8}{3}\) وعلى خط الأعداد.

    سنبدأ بالأعداد الصحيحة 3 و −5. لأنها أسهل طريقة للرسم. انظر الشكل\(\PageIndex{4}\).

    الكسور المناسبة المدرجة هي\(\frac{1}{5}\text{ and } -\frac{4}{5}\). نحن نعلم أن الكسر المناسب\(\frac{1}{5}\) له قيمة أقل من واحد وبالتالي سيكون بين 0 و 1. المقام هو 5، لذلك نقسم الوحدة من 0 إلى 1 إلى 5 أجزاء متساوية\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). نحن نتآمر\(\frac{1}{5}\). انظر الشكل\(\PageIndex{4}\).

    وبالمثل،\(-\frac{4}{5}\) يتراوح بين 0 و−1. بعد تقسيم الوحدة إلى 5 أجزاء متساوية نرسم\(-\frac{4}{5}\). انظر الشكل\(\PageIndex{4}\).

    أخيرًا، انظر إلى الكسور غير الصحيحة\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). هذه هي الكسور التي يكون البسط فيها أكبر من المقام. قد يكون تحديد موقع هذه النقاط أسهل إذا قمت بتغيير كل منها إلى رقم مختلط. انظر الشكل\(\PageIndex{4}\).

    \[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

    \(\PageIndex{4}\)يوضح الشكل خط الأرقام مع رسم جميع النقاط.

    يوجد خط أرقام موضح يمتد من سالب 6 إلى موجب 6. من اليسار إلى اليمين، الأرقام المحددة هي السالب 5، السالب 9/2، السالب 4/5، 1/5، 4/5، 8/3، و 3. يقع الرقم السالب 9/2 في منتصف الطريق بين سالب 5 وسالب 4. الرقم السالب 4/5 يقع قليلاً على يمين السالب 1. الرقم 1/5 يقع قليلاً على يمين 0. الرقم 4/5 على يسار 1 قليلاً. الرقم 8/3 بين 2 و 3، ولكنه أقرب قليلاً إلى 3.
    الشكل\(\PageIndex{4}\)
    التمارين\(\PageIndex{22}\)

    حدد موقع ما يلي وقم بتسميته على سطر الأرقام:\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) و\(\frac{7}{3}\).

    إجابة

    حدد موقع الأعداد الصحيحة، ٤، −٣، وارسمها.

    حدد موقع الكسر المناسب\(\frac{3}{4}\) أولاً. \(\frac{3}{4}\)يقع الكسر بين 0 و1. قسّم المسافة بين 0 و 1 إلى أربعة أجزاء متساوية ثم نرسم\(\frac{3}{4}\). مؤامرة مماثلة\(-\frac{1}{4}\).

    الآن حدد موقع الكسور غير الصحيحة\(\frac{6}{5}\)،\(-\frac{5}{2}\)،\(\frac{7}{3}\). من الأسهل رسمها إذا قمنا بتحويلها إلى أرقام مختلطة ثم رسمها كما هو موضح أعلاه:\(\frac{6}{5} = 1\frac{1}{5}\)،\(-\frac{5}{2} = -2\frac{1}{2}\)،\(\frac{7}{3} = 2\frac{1}{3}\).

    يوجد خط أرقام موضح يمتد من سالب 6 إلى موجب 6. من اليسار إلى اليمين، الأرقام المحددة هي سالب 3، سالب 5/2، سالب 1/4، 3/4، 6/5، 7/3، و 4. الرقم السالب 5/2 يقع في منتصف الطريق بين سالب 3 وسالب 2. الرقم السالب 1/4 يقع قليلاً على يسار 0. الرقم 3/4 يقع قليلاً على يسار 1. الرقم 6/5 يقع قليلاً على يمين 1. الرقم 7/3 بين 2 و 3، ولكنه أقرب قليلاً إلى 2.

    التمارين\(\PageIndex{23}\)

    حدد موقع ما يلي وقم بتسميته على سطر الأرقام:\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) و\(-\frac{8}{3}\).

    إجابة

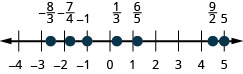
    يوجد خط أرقام موضح يمتد من سالب 4 إلى موجب 5. من اليسار إلى اليمين، الأرقام المحددة هي سالب 8/3، سالب 7/4، سالب 1، 1/3، 6/5، 9/2، و 5. الرقم السالب 8/3 يقع بين سالب 3 وسالب 2 ولكنه أقرب قليلاً إلى سالب 3. الرقم السالب 7/4 يقع قليلاً على يمين السالب 2. الرقم 1/3 يقع قليلاً على يمين 0. الرقم 6/5 يقع قليلاً على يمين 1. الرقم 9/2 يقع في منتصف الطريق بين 4 و 5.

    التمارين\(\PageIndex{24}\)

    حدد موقع ما يلي وقم بتسميته على سطر الأرقام:\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) و\(\frac{8}{3}\).

    إجابة

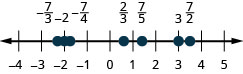
    يوجد خط أرقام موضح يمتد من سالب 4 إلى موجب 5. من اليسار إلى اليمين، الأرقام المحددة هي السالب 7/3، السالب 2، السالب 7/4، 2/3، 7/5، 3، 7/2. الرقم السالب 7/3 يقع بين سالب 3 وسالب 2 ولكنه أقرب قليلاً إلى سالب 2. الرقم السالب 7/4 يقع قليلاً على يمين السالب 2. الرقم 2/3 يقع قليلاً على يسار 1. يقع الرقم 7/5 بين 1 و 2، ولكنه أقرب إلى 1. الرقم 7/2 يقع في منتصف الطريق بين 3 و 4.

    في التمرين\(\PageIndex{25}\)، سنستخدم رموز عدم المساواة لترتيب الكسور. في الفصول السابقة، استخدمنا خط الأعداد لترتيب الأرقام.

    • \(a < b\)«a أقل من b» عندما تكون a على يسار b على خط الأعداد
    • \(a > b\)«a أكبر من b» عندما تكون a على يمين b على خط الأعداد

    عندما ننتقل من اليسار إلى اليمين على خط الأرقام، تزداد القيم.

    التمارين\(\PageIndex{25}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\). قد يكون من المفيد الرجوع إلى الشكل\(\PageIndex{5}\).

    1. \(−\frac{2}{3}\text{___}-1\)
    2. \(−3\frac{1}{2}\text{___}-3\)
    3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
    4. \(−2\text{___}-\frac{8}{3}\)
    يوجد خط أرقام موضح يمتد من سالب 4 إلى موجب 4. من اليسار إلى اليمين، الأرقام المحددة هي سالب 3 و 1/2، وسالب 3، وسالب 8/3، وسالب 2، وسالب 1، وسالب 3/4، وسالب 2/3، وسالب 1/4. الرقم السالب 3 و 1/2 يقع بين سالب 4 وسالب 3 والرقم السالب 8/3 يقع بين سالب 3 وسالب 2، ولكنه أقرب إلى سالب 3. الأرقام السالبة 3/4 والسالبة 2/3 والسالبة 1/4 كلها بين السالب 1 و 0.
    الشكل\(\PageIndex{5}\)
    إجابة

    كن حذرًا عند طلب الأرقام السالبة.

    1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
    4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
    التمارين\(\PageIndex{26}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\).

    1. \(−\frac{1}{3}\text{___}-1\)
    2. \(−1\frac{1}{2}\text{___}-2\)
    3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
    4. \(−3\text{___}-\frac{7}{3}\)
    إجابة
    1. \(>\)
    2. \(>\)
    3. \(<\)
    4. \(<\)
    التمارين\(\PageIndex{27}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\).

    1. \(−1\text{___}-\frac{2}{3}\)
    2. \(−2\frac{1}{4}\text{___}-2\)
    3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
    4. \(−4\text{___}-\frac{10}{3}\)
    إجابة
    1. \(<\)
    2. \(<\)
    3. \(>\)
    4. \(<\)

    حدد موقع الأعداد العشرية على خط الأعداد

    نظرًا لأن الأعداد العشرية هي أشكال من الكسور، فإن تحديد موضع الأعداد العشرية على خط الأعداد يشبه تحديد موقع الكسور على خط الأعداد.

    التمارين\(\PageIndex{28}\)

    حدد موقع 0.4 على خط الأعداد.

    إجابة

    الكسر المناسب له قيمة أقل من واحد. الرقم العشري\(0.4\) يعادل الكسر المناسب\(\frac{4}{10}\)، لذلك\(0.4\) يقع بين 0 و 1. في خط الأعداد، قسّم الفاصل الزمني بين 0 و1 إلى 10 أجزاء متساوية. الآن قم بتسمية الأجزاء\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). نكتب 0 كـ 0.0 و 1 و 1.0، بحيث تكون الأرقام ثابتة في الأجزاء من عشرة. أخيرًا، ضع علامة\(0.4\) على خط الأرقام. انظر الشكل\(\PageIndex{6}\).

    يوجد خط أرقام معروض يمتد من 0.0 إلى 1. النقطة الوحيدة المعطاة هي 0.4، والتي تتراوح بين 0.3 و 0.5.
    الشكل\(\PageIndex{6}\)
    التمارين\(\PageIndex{29}\)

    حدد موقع على خط الأرقام: 0.6.

    إجابة

    يوجد خط أرقام معروض يمتد من 0.0 إلى 1. النقطة الوحيدة المعطاة هي 0.6، والتي تتراوح بين 0.5 و 0.7.

    التمارين\(\PageIndex{30}\)

    حدد موقع على خط الأرقام: 0.9.

    إجابة

    يوجد خط أرقام معروض يمتد من 0.0 إلى 1. النقطة الوحيدة المعطاة هي 0.9، والتي تتراوح بين 0.8 و 1.

    التمارين\(\PageIndex{31}\)

    حدد موقع\(−0.74\) على خط الأرقام.

    إجابة

    الرقم العشري (−0.74\) يعادل\(-\frac{74}{100}\)، لذا فهو يقع بين 0 و−1. على خط الأعداد، ضع علامة على الأجزاء من مائة في الفترة بين 0 و−1. انظر الشكل\(\PageIndex{7}\).

    يوجد خط أرقام موضح يمتد من سالب 1.00 إلى 0.00. النقطة الوحيدة المعطاة هي سالب 0.74، والذي يقع بين سالب 0.8 وسالب 0.7.
    الشكل\(\PageIndex{7}\)
    التمارين\(\PageIndex{32}\)

    حدد الموقع على خط الأعداد: −0.6.

    إجابة

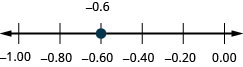
    يوجد خط أرقام موضح يمتد من سالب 1.00 إلى 0.00. النقطة الوحيدة المعطاة هي سالب 0.6، والذي يقع بين سالب 0.8 وسالب 0.4.

    التمارين\(\PageIndex{33}\)

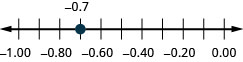
    حدد الموقع على خط الأعداد: −0.7.

    إجابة

    يوجد خط أرقام موضح يمتد من سالب 1.00 إلى 0.00. النقطة الوحيدة المعطاة هي سالب 0.7، والذي يقع بين سالب 0.8 وسالب 0.6.

    أيهما أكبر، 0.04 أم 0.40؟ إذا كنت تفكر في هذا على أنه أموال، فأنت تعلم أن 0.40 دولارًا (أربعين سنتًا) أكبر من 0.04 دولار (أربعة سنتات). لذا،\(0.40 > 0.04\)

    مرة أخرى، يمكننا استخدام خط الأرقام لطلب الأرقام.

    • \(a < b\)«a أقل من b» عندما تكون a على يسار b على خط الأعداد
    • \(a > b\)«a أكبر من b» عندما تكون a على يمين b على خط الأعداد

    أين تقع 0.04 و 0.40 على خط الأعداد؟ انظر الشكل\(\PageIndex{8}\).

    يوجد خط أرقام معروض يتم تشغيله من سالب 0.0 إلى 1.0. من اليسار إلى اليمين، تم وضع علامة على النقاط 0.04 و 0.4. النقطة 0.04 هي بين 0.0 و 0.1. النقطة 0.4 هي بين 0.3 و 0.5.
    الشكل\(\PageIndex{8}\)

    نرى أن 0.40 على يمين 0.04 على خط الأعداد. هذه طريقة أخرى لإثبات ذلك\(0.40 > 0.04\).

    كيف يقارن 0.31 بـ 0.308؟ لا يُترجم هذا إلى أموال لتسهيل المقارنة. ولكن إذا قمنا بتحويل 0.31 و 0.308 إلى كسور، يمكننا معرفة أيهما أكبر.

      0.31 0.308
    قم بالتحويل إلى كسور. \(\frac{31}{100}\) \(\frac{308}{1000}\)
    نحن بحاجة إلى قاسم مشترك لمقارنتها. . .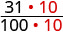
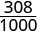      \(\frac{310}{1000}\) \(\frac{308}{1000}\)
    طاولة\(\PageIndex{2}\)

    لأننا نعرف\(310 > 308\) ذلك\(\frac{310}{1000} > \frac{308}{1000}\). لذلك،\(0.31 > 0.308\).

    لاحظ ما فعلناه عند التحويل\(0.31\) إلى كسر - بدأنا بالكسر وانتهينا\(\frac{31}{100}\) بالكسر المكافئ\(\frac{310}{1000}\). التحويل\(\frac{310}{1000}\) مرة أخرى إلى رقم عشري يعطي 0.310. لذا فإن 0.31 يعادل 0.310. كتابة الأصفار في نهاية العدد العشري لا يغير قيمته!

    \[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

    نقول أن 0.31 و 0.310 هي أعداد عشرية مكافئة.

    الأرقام العشرية المكافئة

    يتساوى عددان عشريان إذا تم تحويلهما إلى كسور مكافئة.

    نحن نستخدم الأرقام العشرية المكافئة عندما نقوم بترتيب الكسور العشرية.

    يتم تلخيص الخطوات التي نتخذها لترتيب الكسور العشرية هنا.

    ترتيب الأعداد العشرية.
    1. اكتب العددين واحدًا تحت الآخر، مع ترتيب النقاط العشرية.
    2. تحقق لمعرفة ما إذا كان كلا الرقمين لهما نفس عدد الأرقام. إذا لم يكن الأمر كذلك، فاكتب الأصفار في نهاية الواحد بعدد أقل من الأرقام لجعلها متطابقة.
    3. قارن الأرقام كما لو كانت أرقامًا صحيحة.
    4. رتِّب الأرقام باستخدام علامة عدم المساواة المناسبة.
    التمارين\(\PageIndex{34}\)

    اطلب\(0.64 \text{ ___ } 0.6\) باستخدام\(<\) أو\(>\).

    إجابة

    \(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

    التمارين\(\PageIndex{35}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\):\(0.42 \text{ ___ } 0.4\).

    إجابة

    \(>\)

    التمارين\(\PageIndex{36}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\):\(0.18 \text{ ___ } 0.1\).

    إجابة

    \(>\)

    التمارين\(\PageIndex{37}\)

    اطلب\(0.83 \text{ ___ } 0.803\) باستخدام\(<\) أو\(>\).

    إجابة

    \(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

    التمارين\(\PageIndex{38}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\):\(0.76 \text{ ___ } 0.706\).

    إجابة

    \(>\)

    التمارين\(\PageIndex{39}\)

    رتب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\):\(0.305 \text{ ___ } 0.35\).

    إجابة

    \(<\)

    عند ترتيب الأرقام العشرية السالبة، من المهم تذكر كيفية ترتيب الأعداد الصحيحة السالبة. تذكر أن الأرقام الأكبر موجودة على اليمين على خط الأعداد. على سبيل المثال، نظرًا لأن −2 تقع على يمين -3 على خط الأعداد، فإننا نعرف ذلك\(−2>−3\). وبالمثل، تقع الأرقام الصغيرة على اليسار على خط الأعداد. على سبيل المثال، نظرًا لأن −9 تقع على يسار −6 على خط الأعداد، فإننا نعرف ذلك\(−9<−6\). انظر الشكل\(\PageIndex{9}\).

    يوجد خط أرقام موضح يمتد من سالب 10 إلى 0. لا توجد نقاط محددة وتوجد علامات التجزئة في كل عدد صحيح بين سالب 10 و 0.
    الشكل\(\PageIndex{9}\)

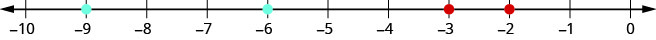
    إذا قمنا بتكبير الفاصل الزمني بين 0 و−1، كما هو موضح في التمرين\(\PageIndex{40}\)، فسوف نرى بنفس الطريقة التي نرى بها\(−0.2>−0.3\) و\(−0.9<−0.6\).

    التمارين\(\PageIndex{40}\)

    استخدم\(<\) أو\(>\) للطلب\(−0.1\text{ ___ }−0.8\).

    إجابة

    \(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

    التمارين\(\PageIndex{41}\)

    اطلب زوج الأرقام التالي باستخدام\(<\) أو\(>\):\(−0.3\text{ ___ }−0.5\).

    إجابة

    \(>\)

    التمارين\(\PageIndex{42}\)

    اطلب زوج الأرقام التالي باستخدام\(<\) أو\(>\):\(−0.6\text{ ___ }−0.7\).

    إجابة

    \(>\)

    المفاهيم الرئيسية


    • \(\sqrt{m}\)تتم قراءة تدوين الجذر التربيعي «الجذر التربيعي لـ»\(m\). إذا\(m = n^{2}\)، إذن\(\sqrt{m} = n\)، من أجل\(n \geq 0\).
    • ترتيب الأعداد العشرية
      1. اكتب العددين واحدًا تحت الآخر، مع ترتيب النقاط العشرية.
      2. تحقق لمعرفة ما إذا كان كلا الرقمين لهما نفس عدد الأرقام. إذا لم يكن الأمر كذلك، فاكتب الأصفار في نهاية الواحد بعدد أقل من الأرقام لجعلها متطابقة.
      3. قارن الأرقام كما لو كانت أرقامًا صحيحة.
      4. رتِّب الأرقام باستخدام علامة عدم المساواة المناسبة.

    الممارسة تجعل من الكمال

    تبسيط التعبيرات باستخدام الجذور التربيعية

    في التمارين التالية، قم بالتبسيط.