1.4: جمع الأعداد الصحيحة وطرحها

أهداف التعلم

• استخدم السلبيات والأضداد
• تبسيط: التعبيرات ذات القيمة المطلقة
• إضافة أعداد صحيحة
• طرح الأعداد الصحيحة

يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي يتم تناولها في هذا القسم في فصل Prealgebra، الأعداد الصحيحة.

استخدم السلبيات والأضداد

لم يتضمن عملنا حتى الآن سوى أرقام العد والأرقام الصحيحة. ولكن إذا سبق لك أن واجهت درجة حرارة أقل من الصفر أو تجاوزت حسابك الجاري عن طريق الخطأ، فأنت على دراية بالفعل بالأرقام السالبة. الأرقام السالبة هي أرقام أقل من\(0\). تظهر الأرقام السالبة على يسار الصفر على خط الأرقام. انظر الشكل\(\PageIndex{1}\).

الشكل\(\PageIndex{1}\). يُظهر خط الأرقام موقع الأرقام الموجبة والسالبة.

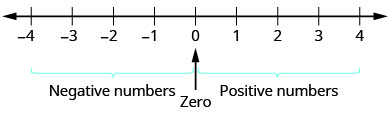
تشير الأسهم الموجودة على طرفي خط الأعداد إلى أن الأرقام تستمر إلى الأبد. لا يوجد أكبر رقم موجب، ولا يوجد أصغر رقم سالب.

هل الصفر رقم موجب أم سالب؟ الأرقام الأكبر من الصفر إيجابية، والأرقام الأصغر من الصفر سالبة. الصفر ليس إيجابيًا ولا سلبيًا.

ضع في اعتبارك كيفية ترتيب الأرقام على خط الأعداد. بالانتقال من اليسار إلى اليمين، تزداد الأرقام في القيمة. بالانتقال من اليمين إلى اليسار، تنخفض الأرقام في القيمة. انظر الشكل\(\PageIndex{2}\).

الشكل\(\PageIndex{2}\). تزداد الأرقام الموجودة على خط الأرقام في القيمة من اليسار إلى اليمين وتنخفض القيمة من اليمين إلى اليسار.

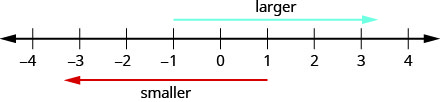
سيساعدك القيام بنشاط الرياضيات المتلاعبة «خط الأرقام - الجزء 2" على تطوير فهم أفضل للأعداد الصحيحة.

تذكر أننا نستخدم الترميز:

\(a \lt b\)(اقرأ «\(a\)أقل من\(b\)») عندما\(a\) تكون\(b\) على يسار خط الأرقام.

\(a \gt b\)(اقرأ «\(a\)أكبر من\(b\)») عندما\(a\) تكون\(b\) على يمين خط الأعداد.

نحتاج الآن إلى توسيع خط الأعداد الذي أظهر الأرقام الكاملة لتشمل الأرقام السالبة أيضًا. الأرقام المميزة بالنقاط في الشكل\(\PageIndex{3}\). تسمى الأعداد الصحيحة. الأعداد الصحيحة هي الأرقام\(...−3, −2, −1, 0, 1, 2, 3…\)

الشكل\(\PageIndex{3}\). جميع الأرقام المميزة تسمى الأعداد الصحيحة.

مثال\(\PageIndex{1}\)

قم بترتيب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\):

1. \(14 \; \_\_\_\; 6\)
2. \(-1\; \_\_\_ \;9\)
3. \(-1\; \_\_\_ -4\)
4. \(\;\; 2 \;\_\_\_ -20\)

الحل:

قد يكون من المفيد الرجوع إلى سطر الأرقام المعروض.

الشكل\(\PageIndex{4}\)

\ (\ ابدأ {محاذاة *} 1. \ رباعي & 14\;\ _\ _\ _\\; 6\\ [4pt]
و 14 > 6 &&\ النص {\(14\)على اليمين أو\(6\) على خط الأرقام.}\\ [8pt]
2. \ رباعي & -1\;\ _\ _\ _\\\; 9\\ [4pt]
& -1 < 9 &\ النص {\(-1\)\(9\)على يسار خط الأرقام.}\\ [8pt]
3. \ رباعية و-1\؛\ _\ _\ _-4\\ [4pt]
& -1 > -4 &&\ النص {\(-1\)على اليمين أو\(-4\) على خط الأرقام.}\\ [8pt]
4. \ رباعي & 2\;\ _\ _\ _\ _-20\\ [4pt]
و 2 > -20 &&\ النص {\(2\)على اليمين\(-20\) أو على خط الأرقام.} \
\ النهاية {محاذاة *}\)

جرب ذلك\(\PageIndex{1}\)

قم بترتيب كل زوج من أزواج الأرقام التالية باستخدام\(<\) or \(>\):

1. \(15 \; \_\_\_\; 7\)
2. \(-2 \; \_\_\_\; 5\)
3. \(-3 \; \_\_\_\; -7\)
4. \(5 \; \_\_\_\; -17\)

Answer

1. \(<\)
2. \(>\)
3. \(<\)
4. \(>\)

Try It \(\PageIndex{2}\)

قم بترتيب كل زوج من أزواج الأرقام التالية باستخدام\(<\) أو\(>\):

1. \(8 \; \_\_\_\; 13\)
2. \(3 \; \_\_\_\; -4\)
3. \(-5 \; \_\_\_\; -2\)
4. \(9 \; \_\_\_\; -21\)

إجابة

1. \(<\)
2. \(>\)
3. \(<\)
4. \(>\)

ربما لاحظت أن الأرقام السالبة، على خط الأعداد، هي صورة معكوسة للأرقام الموجبة، مع وجود صفر في المنتصف. نظرًا لأن الأرقام\(2\)\(−2\) هي نفس المسافة من الصفر، فإنها تسمى s المقابلة. \(2\)نقيضه\(−2\)،\(−2\) ونقيضه\(2\).

مقابل

نقيض الرقم هو الرقم الذي هو نفس المسافة من الصفر على خط الأعداد ولكن على الجانب الآخر من الصفر.

\(\PageIndex{5}\)يوضح الشكل التعريف.

الشكل\(\PageIndex{5}\):\(3\) نقيضه\(−3\).

في بعض الأحيان في الجبر يكون للرمز نفسه معاني مختلفة. تمامًا مثل بعض الكلمات في اللغة الإنجليزية، يصبح المعنى المحدد واضحًا من خلال النظر في كيفية استخدامه. لقد رأيت الرمز «\(−\)» مستخدمًا بثلاث طرق مختلفة.

\ [\ ابدأ {align*} &10 − 4\ رباعي\ نص {بين رقمين، يشير إلى تشغيل}\ textit {الطرح}.\\\\\ qquad\ quad\ text {نقرأ} 10 - 4\،\ النص {باسم «} 10\،\ text {ناقص}\، 4. \ text {»}\\ [5pt]
&-8\ quad\ text {أمام الرقم، يشير إلى}\ textit {سلبي}\\ نص {رقم.}\\\\\\\ quad\ t{ نقرأ} -8\ النص {كـ «ثمانية سالب».}\\ [5pt]
&-x\ quad\ text {يشير أمام المتغير إلى}\ النص المقابل.}\\\\ رباعي\ qquad\ text {نقرأ} -x\ text {على أنه «عكس} x\ text {»}\\ [5pt]
&- (-2)\ quad\ text {هنا توجد علامتان «−».} \\
&\ qquad\ qquad\ text {يخبرنا الرقم الموجود بين قوسين أن الرقم سالب} 2. \\
\ qquad\ qquad\ text {يخبرنا الشخص الموجود خارج الأقواس بأخذ}\ textit {العكس}\ text {of} −2. \\
\ qquad\ qquad\ text {نقرأ} − (−2)\ النص {على أنه «عكس سالب اثنين».} \ النهاية {محاذاة *}\]

الترميز المعاكس

\(−a\)يعني عكس الرقم\(a\).

\(−a\)تتم قراءة الترميز على أنه «عكس»\(a\).

مثال\(\PageIndex{2}\)

ابحث عن:

1. على العكس من\(7\)
2. على العكس من\(−10\)
3. على العكس من\(−(−6)\)

الحل:

1. \( \quad −7\)هي نفس المسافة من\(0\) as\(7\)، ولكن على الجانب الآخر من\(0\). على العكس من\(7\) ذلك\(-7\).

2. \( \quad 10\)هي نفس المسافة من\(0\) as\(−10\)، ولكن على الجانب الآخر من\(0\). على العكس من\(-10\) ذلك\(10\).

3. \(\quad\)على العكس من\(-(-6)\) ذلك\(-6\).

جرب ذلك\(\PageIndex{3}\)

ابحث عن:

1. على العكس من\(4\)
2. the opposite of \(−3\)
3. \(−(−1)\)

Answer

1. \(-4\)
2. \(3\)
3. \(1\)

Try It \(\PageIndex{4}\)

ابحث عن:

1. على العكس من\(8\)
2. على العكس من\(−5\)
3. \(−(−5)\)

إجابة

1. \(-8\)
2. \(5\)
3. \(5\)

يمنحنا عملنا مع الأضداد طريقة لتحديد الأعداد الصحيحة. تسمى الأعداد الصحيحة وأضدادها بالأعداد الصحيحة. الأعداد الصحيحة هي الأرقام\(…−3,−2,−1,0,1,2,3…\)

الأعداد الصحيحة

تسمى الأعداد الصحيحة وأضدادها بالأعداد الصحيحة.

الأعداد الصحيحة هي الأرقام

\[…−3,−2,−1,0,1,2,3… \nonumber \]

عند تقييم عكس المتغير، يجب أن نكون حذرين للغاية. وبدون معرفة ما إذا كان المتغير يمثل عددًا موجبًا أم سالبًا، لا نعرف ما إذا كان −x−x موجبًا أم سالبًا. يمكننا أن نرى هذا في المثال\(\PageIndex{1}\).

مثال\(\PageIndex{3}\):

تقييم

1. \(-x\)، متى\(x = 8\)
2. \(-x\)، متى\(x = -8\)

الحل:

1. 	-x
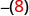
   اكتب عكس العدد ٨.	-8

2. 	-x
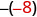
   اكتب عكس -8.	8

جرب ذلك\(\PageIndex{5}\)

تقييم\(-n\), when

1. \(n = 4\)
2. \(n = -4\)

Answer

1. \(-4\)
2. \(4\)

Try It \(\PageIndex{6}\)

قم بالتقييم\(-m\)، متى

1. \(m = 11\)
2. \(m = -11\)

إجابة

1. \(-11\)
2. \(11\)

تبسيط: التعبيرات ذات القيمة المطلقة

لقد رأينا أن الأرقام مثل\(2\) و\(−2\) هي أضداد لأنها\(0\) على نفس المسافة من خط الأعداد. كلاهما وحدتان من\(0\). تُسمى المسافة\(0\) بين أي رقم على خط الأعداد بالقيمة المطلقة لهذا الرقم.

القيمة المطلقة

القيمة المطلقة للرقم هي المسافة من\(0\) على خط الأعداد.

تتم كتابة القيمة المطلقة\(n\) للرقم كـ\(|n|\).

على سبيل المثال،

• \(−5\)تبعد\(5\) الوحدات عن\(0\), وبالتالي\(|−5|=5\).
• \(5\)تبعد\(5\) الوحدات عن\(0\), وبالتالي\(|5|=5\).

\(\PageIndex{6}\)يوضح الشكل هذه الفكرة.

الشكل\(\PageIndex{6}\): الأعداد الصحيحة\(5\)\(5\) والوحدات بعيدة عن\(0\).

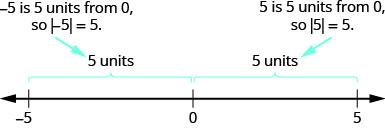
القيمة المطلقة للرقم ليست سالبة أبدًا (لأن المسافة لا يمكن أن تكون سالبة). الرقم الوحيد ذو القيمة المطلقة التي تساوي الصفر هو الرقم صفر نفسه، لأن المسافة من\(0\) إلى\(0\) على خط الأعداد هي صفر وحدة.

خاصية القيمة المطلقة

\(|n| \geq 0\)لجميع الأرقام

تكون القيم المطلقة دائمًا أكبر من أو تساوي الصفر!

يقول علماء الرياضيات ذلك بشكل أكثر دقة، «القيم المطلقة دائمًا ما تكون غير سلبية». غير السالب يعني أكبر من أو يساوي الصفر.

مثال\(\PageIndex{4}\):

قم بالتبسيط:

1. \(|3|\)
2. \(|-44|\)
3. \(|0|\)

الحل:

القيمة المطلقة للرقم هي المسافة بين الرقم والصفر. لا تكون المسافة سالبة أبدًا، لذا فإن القيمة المطلقة لا تكون سالبة أبدًا.

1. \( |3| = 3\)
2. \(|-44| = 44\)
3. \( |0| = 0\)

جرب ذلك\(\PageIndex{7}\)

قم بالتبسيط:

1. \(|4|\)
2. \(|-28|\)
3. \(|0|\)

Answer

1. \(4\)
2. \(28\)
3. \(0\)

Try It \(\PageIndex{8}\)

قم بالتبسيط:

1. \(|-13|\)
2. \(|47|\)

إجابة

1. \(13\)
2. \(47\)

في المثال التالي، سنرتب التعبيرات ذات القيم المطلقة. تذكر أن الأرقام الإيجابية دائمًا ما تكون أكبر من الأرقام السالبة!

مثال\(\PageIndex{5}\):

املأ\(<, >, \text{or} =\) كل زوج من أزواج الأرقام التالية:

1. \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
2. \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
3. \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
4. \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)

الحل:

1. 
   \(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
2. 
   \(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
3. 
   \(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
4. 
   \(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)

جرب ذلك\(\PageIndex{9}\)

املأ\(<, >, \text{or} =\) for each of the following pairs of numbers:

1. \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
2. \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
3. \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
4. \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)

Answer

1. \(>\)
2. \(>\)
3. \(<\)
4. \(>\)

Try It \(\PageIndex{10}\)

املأ\(<, >, \text{or} =\) كل زوج من أزواج الأرقام التالية:

1. \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
2. \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
3. \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
4. \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)

إجابة

1. \(>\)
2. \(>\)
3. \(>\)
4. \(<\)

نضيف الآن أشرطة القيمة المطلقة إلى قائمة رموز التجميع الخاصة بنا. عندما نستخدم ترتيب العمليات، نقوم أولاً بالتبسيط داخل أشرطة القيمة المطلقة قدر الإمكان، ثم نأخذ القيمة المطلقة للرقم الناتج.

رموز التجميع

\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]

في المثال التالي، نقوم بتبسيط التعبيرات داخل أشرطة القيمة المطلقة أولاً، تمامًا كما نفعل مع الأقواس.

مثال\(\PageIndex{6}\):

قم بالتبسيط:\(24 - |19 - 3(6 - 2)|\)

الحل:

\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]

جرب ذلك\(\PageIndex{11}\)

قم بالتبسيط:\(19 - |11 - 4(3 - 1)|\)

Answer

\(16\)

Try It \(\PageIndex{12}\)

قم بالتبسيط:\(9 - |8 - 4(7 - 5)|\)

إجابة

\(9\)

مثال\(\PageIndex{7}\)

تقييم:

1. \(|x|\)عندما\(x = -35\)
2. \(|y|\)عندما\(y = -20\)
3. \(-|u|\)عندما\(u = 12\)
4. \(-|p|\)عندما\(p = -14\)

الحل:

1. \(|x|\)عندما\(x = -35\)

\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)

2. \(|y|\)عندما\(y = -20\)

\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)

3. \(-|u|\)عندما\(u = 12\)

\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)

4. \(-|p|\)عندما\(p = -14\)

\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)

جرب ذلك\(\PageIndex{13}\)

تقييم:

1. \(|x|\) when \(x = -17\)
2. \(|y|\) when \(y = -39\)
3. \(-|m|\) when \(m = 22\)
4. \(-|p|\) when \(p = -11\)

Answer

1. \(17\)
2. \(39\)
3. \(-22\)
4. \(-11\)

Try It \(\PageIndex{14}\)

تقييم:

1. \(|y|\)عندما\(y = -23\)
2. \(|-y|\)عندما\(y = -21\)
3. \(-|n|\)عندما\(n = 37\)
4. \(-|q|\)عندما\(q = -49\)

إجابة

1. \(23\)
2. \(21\)
3. \(-37\)
4. \(-49\)

إضافة أعداد صحيحة

يشعر معظم الطلاب بالراحة تجاه حقائق الجمع والطرح للأرقام الموجبة. لكن القيام بالجمع أو الطرح بالأرقام الإيجابية والسلبية قد يكون أكثر صعوبة.

سيساعدك القيام بنشاط الرياضيات المتلاعبة «إضافة الأرقام الموقعة» على تطوير فهم أفضل لإضافة الأعداد الصحيحة».

سنستخدم عدادين للألوان لنمذجة الجمع والطرح للسلبيات بحيث يمكنك تصور الإجراءات بدلاً من حفظ القواعد.

نترك لونًا واحدًا (أزرق) يمثل إيجابيًا. سيمثل اللون الآخر (الأحمر) السلبيات. إذا كان لدينا عداد إيجابي واحد وعداد سلبي واحد، فإن قيمة الزوج هي صفر. إنهم يشكلون زوجًا محايدًا. قيمة هذا الزوج المحايد هي صفر.

الشكل\(\PageIndex{7}\)

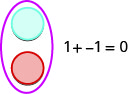
سنستخدم العدادات لإظهار كيفية إضافة حقائق الجمع الأربعة باستخدام الأرقام\(5, −5\) و\(3,−3\).

\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]

للإضافة\(5+3\)، ندرك أن هذا\(5+3\) يعني مجموع\(5\) و\(3\).

نبدأ\(5\) بالإيجابيات.
ثم نضيف\(3\) الإيجابيات.
لدينا الآن\(8\) إيجابيات. مجموع\(5\) و\(3\) هو\(8\).

الآن سنضيف\(−5 + (−3)\). راقب أوجه التشابه مع المثال الأخير\(5 + 3 = 8\).

للإضافة\(−5 + (−3)\)، ندرك أن هذا يعني مجموع\(−5\) و\(−3\).

نبدأ\(5\) بالسلبيات.
ثم نضيف\(3\) السلبيات.
لدينا الآن\(8\) سلبية. مجموع\(-5\) و\(-3\) هو\(-8\).

ما هي الطرق التي كان بها هذان المثالان الأولان متشابهين؟

• يضيف المثال الأول\(5\) الإيجابيات\(3\) والإيجابيات - كلاهما إيجابي.
• يضيف المثال الثاني\(5\)\(3\) السلبيات والسلبيات - كلا السلبيات.

في كل حالة حصلنا على\(8\) - إما\(8\) إيجابيات أو\(8\) سلبيات.

عندما كانت العلامات هي نفسها، كانت العدادات كلها بنفس اللون، ولذا قمنا بإضافتها.

الشكل\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

إضافة:

1. \(1 + 4\)
2. \(-1 + (-4)\)

الحل:

1.

\(1\)\(4\)الإيجابيات الإيجابية هي\(5\) الإيجابيات.

2.

\(1\)السلبيات بالإضافة إلى\(4\) السلبيات هي\(5\) السلبيات.

جرب ذلك\(\PageIndex{15}\)

إضافة:

1. \(2 + 4\)
2. \(-2 + (-4)\)

Answer

1. \(6\)
2. \(-6\)

Try It \(\PageIndex{16}\)

إضافة:

1. \(2 + 5\)
2. \(-2 + (-5)\)

إجابة

1. \(7\)
2. \(-7\)

إذن ماذا يحدث عندما تكون العلامات مختلفة؟ دعونا نضيف\(−5+3\). نحن ندرك أن هذا يعني مجموع\(−5\) و\(3\). عندما كانت العدادات بنفس اللون، وضعناها في صف واحد. عندما تكون العدادات بلون مختلف، نقوم بترتيبها تحت بعضها البعض.

طاولة\(\PageIndex{1}\)

	\(-5 + 3\)يعني مجموع\(-5\) و\(3\).
نبدأ\(5\) بالسلبيات.
ثم نضيف\(3\) الإيجابيات.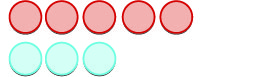
نقوم بإزالة أي أزواج محايدة.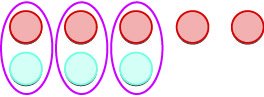
لدينا\(2\) سلبيات متبقية.
مجموع\(-5\) و\(3\) هو\(-2\).	\(-5 + 3 = 2\)

لاحظ أن هناك سلبيات أكثر من الإيجابيات، لذلك كانت النتيجة سلبية.

دعونا الآن نضيف المجموعة الأخيرة،\(5+(−3)\).

طاولة\(\PageIndex{2}\)

	\(5 + (-3)\)يعني مجموع\(-5\) و\(-3\).
نبدأ\(5\) بالإيجابيات.
ثم نضيف\(3\) السلبيات.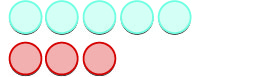
نقوم بإزالة أي أزواج محايدة.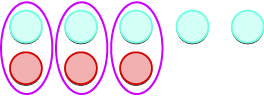
لدينا\(2\) إيجابيات متبقية.
مجموع\(5\) و\(-3\) هو\(2\).	\(5 + (-3) = 2\)

عندما نستخدم العدادات لتمثيل إضافة الأعداد الصحيحة الموجبة والسالبة، يكون من السهل معرفة ما إذا كانت هناك عدادات أكثر إيجابية أو أكثر سالبة. لذلك نحن نعرف ما إذا كان المبلغ سيكون موجبًا أم سلبيًا.

الشكل\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

إضافة:

1. \(-1 + 5\)
2. \(1 + (-5)\)

الحل:

1. \(-1 + 5\)

هناك المزيد من الإيجابيات، لذا فإن المجموع إيجابي.

لذلك،\(-1 + 5 = 4\).

2. \(1 + (-5)\)

هناك المزيد من السلبيات، وبالتالي فإن المجموع سلبي.

لذا،\(1 + (-5) = -4\)

جرب ذلك\(\PageIndex{17}\)

إضافة:

1. \(-2 + 4\)
2. \(2 + (-4)\)

Answer

1. \(2\)
2. \(-2\)

Try It \(\PageIndex{18}\)

إضافة:

1. \(-2 + 5\)
2. \(2 + (-5)\)

إجابة

1. \(3\)
2. \(-3\)

الآن بعد أن أضفنا أعدادًا صغيرة إيجابية وسلبية مع نموذج، يمكننا تصور النموذج في أذهاننا لتبسيط المشكلات مع أي أرقام.

عندما تحتاج إلى إضافة أرقام مثل\(37+(−53)\)، فأنت لا تريد حقًا حساب العدادات\(37\) الزرقاء والعدادات\(53\) الحمراء. مع وجود النموذج في ذهنك، هل يمكنك تصور ما ستفعله لحل المشكلة؟

عدادات الصورة\(37\) الزرقاء مع عدادات\(53\) حمراء تصطف تحتها. نظرًا لوجود عدادات حمراء (سالبة) أكثر من العدادات الزرقاء (الإيجابية)، سيكون المجموع سالبًا. كم عدد العدادات الحمراء الأخرى التي ستكون موجودة؟ لأن\(53−37=16\) هناك\(16\) المزيد من العدادات الحمراء.

لذلك، مجموع\(37+(−53)\) هو\(−16\).

\[37+(−53)=−16\nonumber\]

دعونا نجرب واحدة أخرى. سنقوم بإضافة\(−74+(−27)\). مرة أخرى، تخيل العدادات\(74\) الحمراء\(27\) والمزيد من العدادات الحمراء، لذلك سيكون لدينا عدادات\(101\) حمراء. هذا يعني أن المبلغ هو\(−101\).

\[−74+(−27)=−101\nonumber\]

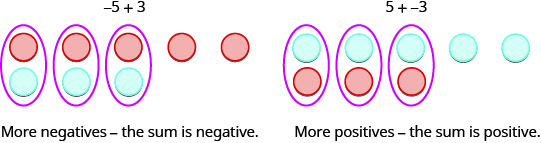
دعونا ننظر مرة أخرى إلى نتائج إضافة مجموعات مختلفة من\(5,−5\) و\(3, -3\).

إضافة الأعداد الصحيحة الإيجابية والسلبية

\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both positive, sum positive}} \end{array}\nonumber\]

عندما تكون العلامات هي نفسها، ستكون العدادات كلها بنفس اللون، لذا قم بإضافتها.

\[\begin{array} {ll} {5 + 3=-2} &{-5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]

عندما تكون العلامات مختلفة، قد تشكل بعض العدادات أزواجًا محايدة، لذا اطرح لمعرفة العدد المتبقي.

قم بتصوير النموذج وأنت تقوم بتبسيط التعبيرات في الأمثلة التالية.

مثال\(\PageIndex{10}\)

قم بالتبسيط:

1. \(19 + (-47)\)
2. \(-14 + (-36)\)

الحل:

1. بما أن العلامات مختلفة، فإننا نطرح\(19\) منها\(47\). ستكون الإجابة سلبية لأن هناك سلبيات أكثر من الإيجابيات.

\(\text{Add.} \qquad 19 + (-47) = -28\)

2. بما أن العلامات هي نفسها، نضيف. ستكون الإجابة سلبية لأن هناك سلبيات أكثر من الإيجابيات.

\(\text{Add.} \qquad-14 + (-36) = -50\)

جرب ذلك\(\PageIndex{19}\)

قم بالتبسيط:

1. \(-31 + (-19)\)
2. \(15 + (-32)\)

Answer

1. \(-50\)
2. \(-17\)

Try It \(\PageIndex{20}\)

قم بالتبسيط:

1. \(-42 + (-28)\)
2. \(25 + (-61)\)

إجابة

1. \(-70\)
2. \(-36\)

تمتد التقنيات المستخدمة حتى الآن إلى مشاكل أكثر تعقيدًا، مثل تلك التي رأيناها من قبل. تذكر اتباع ترتيب العمليات!

مثال\(\PageIndex{11}\)

قم بالتبسيط:

\(-5 + 3(-2 + 7)\)

الحل:

\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]

جرب ذلك\(\PageIndex{21}\)

قم بالتبسيط:

\(-2 + 5(-4 + 7)\)

Answer

\(13\)

Try It \(\PageIndex{22}\)

قم بالتبسيط:

\(-4 + 2(-3 + 5)\)

إجابة

\(0\)

طرح الأعداد الصحيحة

ملاحظة

سيساعدك القيام بنشاط الرياضيات المتلاعبة «طرح الأرقام الموقعة» على تطوير فهم أفضل لطرح الأعداد الصحيحة.

سنستمر في استخدام العدادات لتمثيل الطرح. تذكر أن العدادات الزرقاء تمثل الأرقام الموجبة والعدادات الحمراء تمثل الأرقام السالبة.

ربما عندما كنت أصغر سنًا، كنت تقرأ «\(5−3\)» كـ «\(5\)take away»\(3\). عند استخدام العدادات، يمكنك التفكير في الطرح بنفس الطريقة!

سنمثل حقائق الطرح الأربعة باستخدام الأرقام\(5\) و\(3\).

\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]

للطرح\(5−3\)، نعيد ذكر المشكلة باسم «\(5\)take away»\(3\).

طاولة\(\PageIndex{3}\)

نبدأ\(5\) بالإيجابيات.
نحن «نزيل»\(3\) الإيجابيات.
لدينا\(2\) إيجابيات متبقية.
الفرق بين\(5\) و\(3\) هو\(2\).	\(2\)

الآن سنطرح\(−5−(−3)\). راقب أوجه التشابه مع المثال الأخير\(5−3=2\).

للطرح\(−5−(−3)\)، نعيد ذكر هذا بـ «\(–5\)take away\(–3\)»

طاولة\(\PageIndex{4}\)

نبدأ\(5\) بالسلبيات.
نحن «نزيل»\(3\) السلبيات.
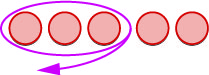لدينا\(2\) سلبيات متبقية.
الفرق بين\(-5\) و\(-3\) هو\(-2\).	\(-2\)

لاحظ أن هذين المثالين متشابهان إلى حد كبير: المثال الأول، نطرح 3 إيجابيات من 5 إيجابيات وننتهي بإيجابيتين.

في المثال الثاني، نطرح 3 سلبيات من 5 سلبيات وننتهي بـ 2 سلبيات.

استخدم كل مثال عدادات بلون واحد فقط، وكان نموذج «take away» للطرح سهل التطبيق.

الشكل\(\PageIndex{9}\)

مثال\(\PageIndex{12}\)

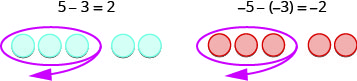
طرح:

1. \(7 - 5\)
2. \(-7 - (-5)\)

الحل:

1. \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
2. \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]

جرب ذلك\(\PageIndex{23}\)

طرح:

1. \(6 - 4\)
2. \(-6 - (-4)\)

Answer

1. \(2\)
2. \(-2\)

Try It \(\PageIndex{24}\)

طرح:

1. \(7 - 4\)
2. \(-7 - (-4)\)

إجابة

1. \(3\)
2. \(-3\)

ماذا يحدث عندما يتعين علينا طرح عدد موجب واحد وعدد سالب واحد؟ سنحتاج إلى استخدام كل من العدادات البيضاء والحمراء بالإضافة إلى بعض الأزواج المحايدة. لا تؤدي إضافة زوج محايد إلى تغيير القيمة. إنه مثل تغيير الأرباع إلى النيكل - القيمة هي نفسها، لكنها تبدو مختلفة.

• للطرح\(−5−3\)، نعيد ذكر ذلك على\(−5\) أنه سحب\(3\).

نبدأ\(5\) بالسلبيات. نحن بحاجة إلى التخلص من\(3\) الإيجابيات، ولكن ليس لدينا أي إيجابيات نستخلصها.

تذكر أن الزوج المحايد له قيمة صفر. إذا أضفنا\(0\) إلى\(5\) قيمتها فلا يزال\(5\). نضيف أزواجًا محايدة إلى\(5\) السلبيات حتى نحصل على\(3\) الإيجابيات التي يجب التخلص منها.

طاولة\(\PageIndex{5}\)

	\(-5 -3\)يعني\(-5\) يسلب\(3\)
نبدأ\(5\) بالسلبيات.
نضيف الآن المحايدين اللازمين للحصول على\(3\) الإيجابيات.
نزيل\(3\) الإيجابيات.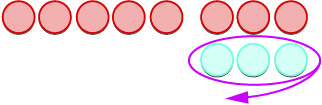
لقد تركنا مع\(8\) السلبيات.
الفرق بين\(-5\) و\(3\) هو\(-8\).	\(-5 - 3 = -8\)

والآن، الحالة الرابعة،\(5−(−3)\). نبدأ\(5\) بالإيجابيات. نحن بحاجة إلى إزالة\(3\) السلبيات، ولكن لا توجد سلبيات يمكن إزالتها. لذلك نضيف أزواجًا محايدة حتى نحصل على\(3\) سلبيات يجب إزالتها.

طاولة\(\PageIndex{6}\)

	\(5 -(-3)\)يعني\(5\) يسلب\(-3\)
نبدأ\(5\) بالإيجابيات.
نضيف الآن الأزواج المحايدة المطلوبة.
نزيل\(3\) السلبيات.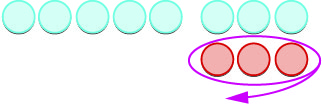
لدينا الكثير من\(8\) الإيجابيات.
الفرق بين\(5\) و\(-3\) هو\(8\).	\(5 - (-3) = 8\)

مثال\(\PageIndex{13}\)

طرح:

1. \(-3 -1\)
2. \(3 - (-1)\)

الحل:

1.

خذ 1 إيجابيًا من الزوج المحايد المضاف.

\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\)

2.

خذ سالبًا واحدًا من الزوج المحايد المضاف.

\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\)

جرب ذلك\(\PageIndex{25}\)

طرح:

1. \(-6 -4\)
2. \(6 - (-4)\)

Answer

1. \(-10\)
2. \(10\)

Try It \(\PageIndex{26}\)

طرح:

1. \(-7-4\)
2. \(7 - (-4)\)

إجابة

1. \(-11\)
2. \(11\)

هل لاحظت أن طرح الأرقام الموقعة يمكن أن يتم بإضافة العكس؟ في التمرين\(\PageIndex{33}\)،\(−3−1\) هو نفسه\(−3+(−1)\)\(3−(−1)\) وهو نفسه\(3+1\). غالبًا ما سترى هذه الفكرة، خاصية الطرح، مكتوبة على النحو التالي:

خاصية الطرح

\[a−b=a+(−b) \nonumber\]

طرح رقم هو نفس إضافة نقيضه.

انظر إلى هذين المثالين.

الشكل\(\PageIndex{10}\):\(6−4\) يعطي نفس الإجابة مثل\(6+(−4)\).

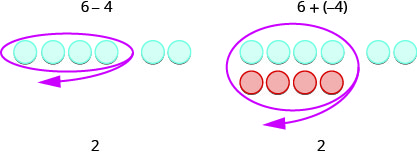
بالطبع، عندما تكون لديك مشكلة طرح تحتوي على أرقام موجبة فقط، مثل\(6−4\)، تقوم فقط بعملية الطرح. لقد عرفت بالفعل كيفية الطرح منذ\(6−4\) فترة طويلة. لكن معرفة ذلك\(6−4\) يعطي نفس الإجابة التي\(6+(−4)\) تساعد عند طرح الأرقام السالبة. تأكد من أنك تفهم كيف\(6−4\)\(6+(−4)\) وتعطي نفس النتائج!

مثال\(\PageIndex{14}\)

قم بالتبسيط:

1. \(13 - 8 \space \text{and } 13 + (-8)\)
2. \(-17 - 9 \space \text{and } -17 + (-9)\)

الحل:

1. \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
2. \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)

جرب ذلك\(\PageIndex{27}\)

قم بالتبسيط:

1. \(21 - 13 \space \text{and } 21 + (-13)\)
2. \(-11 - 7 \space \text{and } -11 + (-7)\)

Answer

1. \(8\)
2. \(-18\)

Try It \(\PageIndex{28}\)

قم بالتبسيط:

1. \(15 - 7 \space \text{and } 15 + (-7)\)
2. \(-14 - 8 \space \text{and } -14 + (-8)\)

إجابة

1. \(8\)
2. \(-22\)

انظر إلى ما يحدث عندما نطرح سالبًا.

الشكل\(\PageIndex{11}\):\(8−(−5)\) يعطي نفس الإجابة\(8+5\)

طرح رقم سالب يشبه إضافة رقم موجب!

غالبًا ما سترى هذا مكتوبًا كـ\(a−(−b)=a+b\).

هل يصلح ذلك للأرقام الأخرى أيضًا؟ دعونا نفعل المثال التالي ونرى.

مثال\(\PageIndex{15}\)

قم بالتبسيط:

1. \(9 - (-15) \space \text{and } 9 + 15\)
2. \(-7 - (-4) \space \text{and } -7 + 4\)

الحل:

1. \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
2. \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)

جرب ذلك\(\PageIndex{29}\)

قم بالتبسيط:

1. \(6 - (-13) \space \text{and } 6 + 13\)
2. \(-5 - (-1) \space \text{and } -5 + 1\)

Answer

1. \(19\)
2. \(-4\)

Try It \(\PageIndex{30}\)

قم بالتبسيط:

1. \(4 - (-19) \space \text{and } 4 + 19\)
2. \(-4 - (-7) \space \text{and } -4 + 7\)

إجابة

1. \(23\)
2. \(3\)

دعونا ننظر مرة أخرى إلى نتائج طرح المجموعات المختلفة من\(5,−5\) و\(3,−3\).

طرح الأعداد الصحيحة

\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]

عندما يكون هناك عدد كافٍ من عدادات اللون لأخذها، اطرح.

\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]

عندما لا تكون هناك عدادات كافية للون لإزالتها، قم بإضافتها.

ماذا يحدث عندما يكون هناك أكثر من ثلاثة أعداد صحيحة؟ نحن فقط نستخدم ترتيب العمليات كالمعتاد.

مثال\(\PageIndex{16}\)

قم بالتبسيط:

\(7 - (-4 -3) - 9\)

الحل:

\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]

جرب ذلك\(\PageIndex{31}\)

قم بالتبسيط:

\(8−(−3−1)−9\)

Answer

\(3\)

Try It \(\PageIndex{32}\)

قم بالتبسيط:

\(12−(−9−6)−14\)

إجابة

\(12\)

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع إضافة الأعداد الصحيحة وطرحها. ستحتاج إلى تمكين Java في متصفح الويب الخاص بك لاستخدام التطبيقات.

• إضافة شريحة ملونة
• اطرح الرقاقة الملونة

المفاهيم الرئيسية

• جمع الأعداد الصحيحة الموجبة والسالبة

\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]

\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]

• خاصية القيمة المطلقة:

\(|n| \geq 0\)لجميع الأرقام. تكون القيم المطلقة دائمًا أكبر من أو تساوي الصفر!

• طرح الأعداد الصحيحة

\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]

\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]

• خاصية الطرح: طرح رقم هو نفس إضافة نقيضه.

مسرد المصطلحات

القيمة المطلقة

القيمة المطلقة للرقم هي المسافة من 0 على خط الأعداد. تتم كتابة القيمة المطلقة للرقم nn كـ |n|.

الأعداد الصحيحة

تسمى الأرقام الصحيحة وأضدادها بالأعداد الصحيحة:\(...−3, −2, −1, 0, 1, 2, 3...\)

مقابل

نقيض العدد هو العدد الذي هو نفس المسافة من الصفر على خط الأعداد ولكن على الجانب الآخر من الصفر: −\(a\) يعني عكس العدد. \(a\)تتم قراءة الترميز - «عكس»\(a\).