Skip to main content
Global

11.5E: تمارين

  1. Last updated
  2. Save as PDF
  • Page ID
    201802

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    الممارسة تجعل من الكمال

    التمارين الرياضية\(\PageIndex{13}\) Graph a Hyperbola with Center at \((0,0)\)

    في التمارين التالية، رسم بياني.

    1. \(\frac{x^{2}}{9}-\frac{y^{2}}{4}=1\)
    2. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    3. \(\frac{x^{2}}{16}-\frac{y^{2}}{25}=1\)
    4. \(\frac{x^{2}}{9}-\frac{y^{2}}{36}=1\)
    5. \(\frac{y^{2}}{25}-\frac{x^{2}}{4}=1\)
    6. \(\frac{y^{2}}{36}-\frac{x^{2}}{16}=1\)
    7. \(16 y^{2}-9 x^{2}=144\)
    8. \(25 y^{2}-9 x^{2}=225\)
    9. \(4 y^{2}-9 x^{2}=36\)
    10. \(16 y^{2}-25 x^{2}=400\)
    11. \(4 x^{2}-16 y^{2}=64\)
    12. \(9 x^{2}-4 y^{2}=36\)
    إجابة

    1.

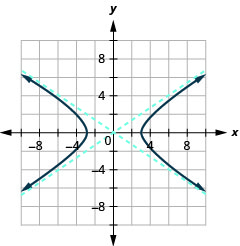
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، حيث تكون خطوط التقارب y تساوي زائد أو ناقص الثلثين في x، والفروع التي تمر عبر القمم (زائد أو ناقص 3، 0) وتفتح يمينًا ويسارًا.
    الشكل 11.4.33

    3.

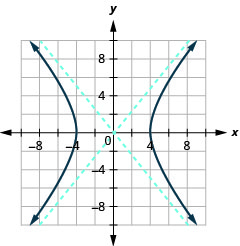
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، حيث إن خطوط التقارب y تساوي زائد أو ناقص خمسة أرباع في x، والفروع التي تمر عبر القمم (زائد أو ناقص 4، 0) وتفتح يمينًا ويسارًا.
    الشكل 11.4.34

    5.

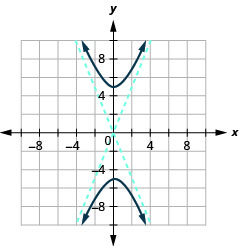
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، حيث إن خطوط التقارب y تساوي زائد أو ناقص خمسة أنصاف في x، والفروع التي تمر عبر القمم (0، زائد أو ناقص 5) وتنفتح لأعلى ولأسفل.
    الشكل 11.4.35

    7.

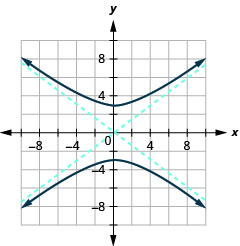
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي بحيث تكون خطوط التقارب y تساوي زائد أو ناقص ثلاثة أرباع في x، والفروع التي تمر عبر الرؤوس (0، زائد أو ناقص 3) وتفتح لأعلى ولأسفل.
    الشكل 11.4.36

    9.

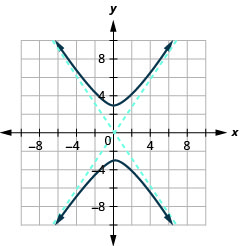
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، حيث إن خطوط التقارب y تساوي زائد أو ناقص ثلاثة أنصاف في x، والفروع التي تمر عبر القمم (0، زائد أو ناقص 3) وتفتح لأعلى ولأسفل.
    الشكل 11.4.37

    11.

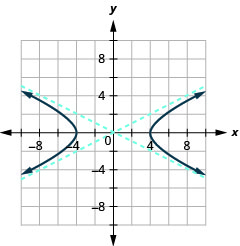
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، حيث إن خطوط التقارب y تساوي زائد أو ناقص نصف مضروبًا في x، والفروع التي تمر عبر القمم (زائد أو ناقص 4، 0) وتفتح يمينًا ويسارًا.
    الشكل 11.4.38
    التمارين الرياضية\(\PageIndex{14}\) Graph a Hyperbola with Center at \((h,k)\)

    في التمارين التالية، رسم بياني.

    1. \(\frac{(x-1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y-4)^{2}}{9}-\frac{(x-2)^{2}}{25}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-4)^{2}}{16}=1\)
    5. \(\frac{(y+4)^{2}}{25}-\frac{(x+1)^{2}}{36}=1\)
    6. \(\frac{(y+1)^{2}}{16}-\frac{(x+1)^{2}}{4}=1\)
    7. \(\frac{(y-4)^{2}}{16}-\frac{(x+1)^{2}}{25}=1\)
    8. \(\frac{(y+3)^{2}}{16}-\frac{(x-3)^{2}}{36}=1\)
    9. \(\frac{(x-3)^{2}}{25}-\frac{(y+2)^{2}}{9}=1\)
    10. \(\frac{(x+2)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
    إجابة

    1.

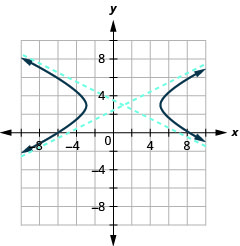
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (1، 3) وخط التقارب الذي يمر عبر (سالب 3، 1) و (5، 5) وخط التقارب الذي يمر خلال (5، 1) و (سالب 3، 5)، والفروع التي تمر عبر القمم (سالب 3، 3) و (5، 3) و يفتح يمينًا ويسارًا.
    الشكل 11.4.39

    3.

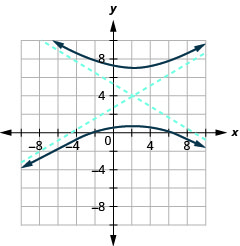
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (1، 3) وخط التقارب الذي يمر عبر (سالب 3، 1) و (5، 5) وخط التقارب الذي يمر خلال (5، 1) و (سالب 3، 5)، والفروع التي تمر عبر القمم (سالب 3، 3) و (5، 3) و يفتح يمينًا ويسارًا.
    الشكل 11.4.40

    5.

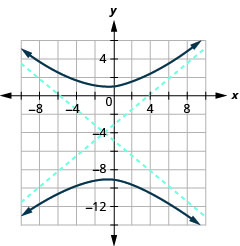
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (1، سالب 4) وخط التقارب الذي يمر عبر (سالب 7، 1) و (5، سالب 9) وخط التقارب الذي يمر خلال (5، 1) و (سالب 7، سالب 9)، والفروع التي تمر عبر القمم (1، 1) و (1، سلبي 9) وافتح لأعلى ولأسفل.
    الشكل 11.4.41

    7.

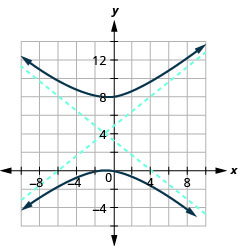
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (سالب 1، 4) وخط التقارب الذي يمر خلال (4، 8) و (سالب 6، 0) وخط التقارب الذي يمر عبره (سالب 6، 8) و (4، 0)، والفروع التي تمر عبر القمم (سالب 1، 0) و ( سلبي 1، 8) وافتح لأعلى ولأسفل.
    الشكل 11.4.42

    9.

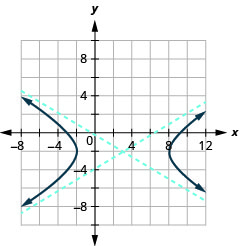
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (3، سالب 2) وخط التقارب الذي يمر خلال (8، 1) و (سالب 2، سالب 5) وخط التقارب الذي يمر خلال (سالب 2، سالب 1) و (8، سالب 5)، والفروع التي تمر عبر الرؤوس (سالبة 2، سالبة 2) و (8، سالبة 2) وتفتح يسارًا ويمينًا.
    الشكل 11.4.43
    التمارين الرياضية\(\PageIndex{15}\) Graph a Hyperbola with Center at \((h,k)\)

    في التمارين التالية،

    1. اكتب المعادلة في الصورة القياسية و
    2. رسم بياني.
    1. \(9 x^{2}-4 y^{2}-18 x+8 y-31=0\)
    2. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
    3. \(y^{2}-x^{2}-4 y+2 x-6=0\)
    4. \(4 y^{2}-16 x^{2}-24 y+96 x-172=0\)
    5. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
    إجابة

    1.

    1. \(\frac{(x-1)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
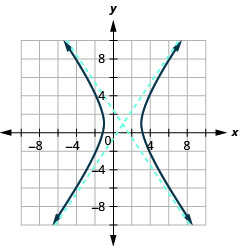
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (1، 1) وخط التقارب الذي يمر خلال (3، 4) و (سالب 1، سالب 2) وخط التقارب الذي يمر خلال (سالب 1، 4) و (3، سالب 2)، والفروع التي تمر عبر القمم (سالب 1، 1) و (3، 1) ويفتح يسارًا ويمينًا.
    الشكل 11.4.44

    3.

    1. \(\frac{(y-2)^{2}}{9}-\frac{(x-1)^{2}}{9}=1\)
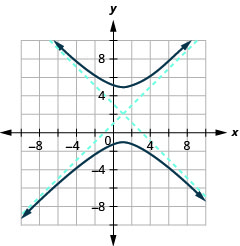
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (1، 2) وخط التقارب الذي يمر خلال (4، 5) و (سالب 2، سالب 1) وخط التقارب الذي يمر عبره (سالب 2، 5) و (4، سالب 1)، والفروع التي تمر عبر القمم (1، 5) و ( 1، سلبي 1) وافتح لأعلى ولأسفل.
    الشكل 11.4.45

    5.

    1. \(\frac{(y+1)^{2}}{1}-\frac{(x+2)^{2}}{9}=1\)
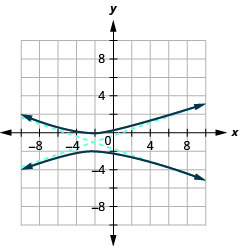
    يوضِّح الرسم البياني محور س والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي مع المركز (سالب 2، سالب 1) وخط التقارب الذي يمر خلال (1، 0) و (سالب 5، سالب 2) وخط التقارب الذي يمر خلال (3، 0) و (1، سالب 2)، والفروع التي تمر عبر القمم ( سالب 2، 0) و (سالب 2، سالب 2) وافتح لأعلى ولأسفل.
    الشكل 11.4.46
    التمارين الرياضية\(\PageIndex{16}\) Identify the Graph of each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    في التمارين التالية، حدد نوع الرسم البياني.

      1. \(x=-y^{2}-2 y+3\)
      2. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
      3. \(9 x^{2}+25 y^{2}=225\)
      4. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      1. \(x=-2 y^{2}-12 y-16\)
      2. \(x^{2}+y^{2}=9\)
      3. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
      4. \(16 x^{2}+36 y^{2}=576\)
    إجابة

    2.

    1. بارابولا
    2. دائرة
    3. هايبربولا
    4. الشكل البيضاوي
    التمارين\(\PageIndex{17}\) Mixed Practice

    في التمارين التالية، قم برسم بياني لكل معادلة.

    1. \(\frac{(y-3)^{2}}{9}-\frac{(x+2)^{2}}{16}=1\)
    2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
    3. \(y=(x-1)^{2}+2\)
    4. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    5. \((x+2)^{2}+(y-5)^{2}=4\)
    6. \(9 x^{2}-4 y^{2}+54 x+8 y+41=0\)
    7. \(x=-y^{2}-2 y+3\)
    8. \(16 x^{2}+9 y^{2}=144\)
    إجابة

    2.

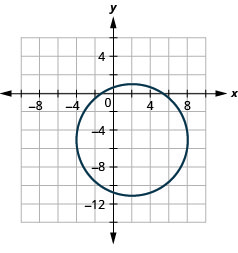
    يوضِّح التمثيل البياني المستوى الإحداثي x y مع دائرة مركزها (2، سالب 5) ونصف قطرها 6 وحدات.
    الشكل 11.4.47

    4.

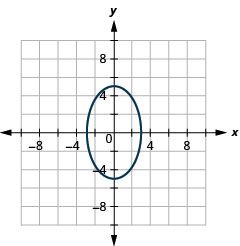
    يُظهر الرسم البياني المستوى الإحداثي x y مع الشكل البيضاوي الذي يكون محوره الرئيسي عموديًا، والرؤوس هي (0، زائد أو ناقص 5) والرؤوس المشتركة هي (زائد أو ناقص 3، 0).
    الشكل 11.4.48

    6.

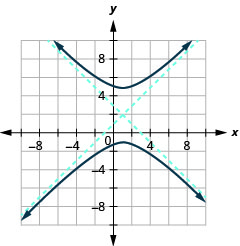
    يوضِّح التمثيل البياني المستوى الإحداثي x y مع المركز (1، 2) وخط التقارب الذي يمر عبر (سالب 2، 5) و (5، سالب 1) وخط التقارب الذي يمر عبر (4، 5) و (2، 0)، والفروع التي تمر بالرءوس (1، 5) و (سالب 2، سالب 1) وتفتح لأعلى ولأسفل.
    الشكل 11.4.49

    8.

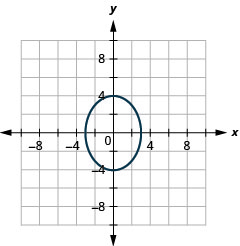
    يُظهر الرسم البياني المستوى الإحداثي x y مع الشكل البيضاوي الذي يكون محوره الرئيسي عموديًا، والرؤوس هي (0، زائد أو ناقص 4) والرؤوس المشتركة هي (زائد أو ناقص 3، 0).
    الشكل 11.4.50
    التمارين\(\PageIndex{18}\) Writing Exercises
    1. بكلماتك الخاصة، حدد الهيبربولا واكتب معادلة الهيبربولا التي تتمركز عند الأصل في الشكل القياسي. ارسم رسمًا تخطيطيًا للهايبربولا الذي يصف المركز والرؤوس وخطوط التقارب.
    2. اشرح بكلماتك الخاصة كيفية إنشاء واستخدام المستطيل الذي يساعد في رسم hyperbola في رسم بياني.
    3. قارن وقارن بين الرسوم البيانية للمعادلات\(\frac{x^{2}}{4}-\frac{y^{2}}{9}=1\) و\(\frac{y^{2}}{9}-\frac{x^{2}}{4}=1\).
    4. اشرح بكلماتك الخاصة، كيفية التمييز بين معادلة القطع الناقص ومعادلة hyperbola.
    إجابة

    2. قد تختلف الإجابات

    4. قد تختلف الإجابات

    فحص ذاتي

    أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

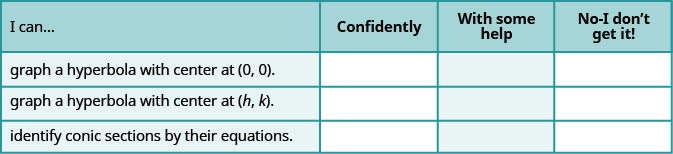
    يحتوي هذا الجدول على أربعة أعمدة وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي كل عمود، «لا أستطيع»، «بثقة»، «مع بعض المساعدة،» و «لا يمكنني الحصول عليه»™! †في الصف الثاني، كان الرسم البياني لـ I عبارة عن رسم بياني لهايبربولا في المركز (0، 0). في الصف 3، كان الرسم البياني لـ I عبارة عن رسم بياني لـ hyperbola مع مركز عند (h، k). في الصف 4، كان بإمكاني تحديد المقاطع المخروطية من خلال معادلاتها.
    الشكل 11.4.51

    ب- على مقياس من 1 إلى 10، كيف تقيم إتقانك لهذا القسم في ضوء إجاباتك على قائمة التحقق؟ كيف يمكنك تحسين هذا؟