11.6: حل أنظمة المعادلات غير الخطية
- Page ID
- 201780
في نهاية هذا القسم، ستكون قادرًا على:
- حل نظام المعادلات غير الخطية باستخدام الرسوم البيانية
- حل نظام المعادلات غير الخطية باستخدام الاستبدال
- حل نظام المعادلات غير الخطية باستخدام الحذف
- استخدم نظام المعادلات غير الخطية لحل التطبيقات
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.\).
إذا فاتتك هذه المشكلة، راجع المثال 4.2. - حل النظام عن طريق الاستبدال:\(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
إذا فاتتك هذه المشكلة، راجع المثال 4.7. - حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)
إذا فاتتك هذه المشكلة، راجع المثال 4.9.
حل نظام المعادلات غير الخطية باستخدام التمثيل البياني
لقد تعلمنا كيفية حل أنظمة المعادلات الخطية بمتغيرين عن طريق الرسم البياني والاستبدال والحذف. سنستخدم هذه الأساليب نفسها عندما ننظر إلى أنظمة المعادلات غير الخطية ذات المعادلتين والمتغيرين. نظام المعادلات غير الخطية هو نظام لا تكون فيه واحدة على الأقل من المعادلات خطية.
على سبيل المثال، يعد كل نظام من الأنظمة التالية نظامًا من المعادلات غير الخطية.
\(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right. \left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right. \left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.\)
نظام المعادلات غير الخطية هو نظام لا تكون فيه واحدة على الأقل من المعادلات خطية.
تمامًا كما هو الحال مع أنظمة المعادلات الخطية، فإن حل النظام غير الخطي هو زوج مرتب يجعل كلتا المعادلتين صحيحتين. في النظام غير الخطي، قد يكون هناك أكثر من حل. سنرى هذا عندما نحل نظامًا من المعادلات غير الخطية بالرسم البياني.
عندما قمنا بحل أنظمة المعادلات الخطية، كان حل النظام هو نقطة تقاطع الخطين. في أنظمة المعادلات غير الخطية، قد تكون الرسوم البيانية عبارة عن دوائر أو أشكال مماثلة أو مبالغ زائدة وقد تكون هناك عدة نقاط تقاطع، وبالتالي العديد من الحلول. بمجرد تحديد الرسوم البيانية، قم بتصور الطرق المختلفة التي يمكن أن تتقاطع بها الرسوم البيانية وبالتالي عدد الحلول التي قد تكون موجودة.
لحل أنظمة المعادلات غير الخطية بالرسم البياني، نستخدم بشكل أساسي نفس الخطوات كما هو الحال مع أنظمة المعادلات الخطية المعدلة قليلاً للمعادلات غير الخطية. يتم سرد الخطوات أدناه كمرجع.
حل نظام المعادلات غير الخطية بالرسم البياني.
- حدد الرسم البياني لكل معادلة. ارسم الخيارات الممكنة للتقاطع.
- ارسم المعادلة الأولى بيانيًا.
- ارسم المعادلة الثانية على نفس نظام الإحداثيات المستطيلة.
- حدد ما إذا كانت الرسوم البيانية تتقاطع.
- حدد نقاط التقاطع.
- تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين.
حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{x-y=-2} \\ {y=x^{2}}\end{array}\right.\)
الحل:
| حدد كل رسم بياني. | \(\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.\) |
| ارسم الخيارات الممكنة لتقاطع القطع المكافئ والخط. | 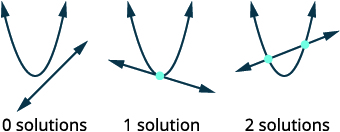 |
|
رسم الخط،\(x-y=-2\). شكل اعتراض المنحدر\(y=x+2\). رسم بياني للقطع المكافئ،\(y=x^{2}\). |
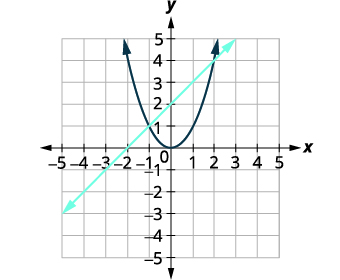 |
| حدد نقاط التقاطع. | يبدو أن نقاط التقاطع هي\((2,3)\) و\((-1,1)\). |
|
تحقق للتأكد من أن كل حل يجعل كلا المعادلتين صحيحتين. \((2,4)\) \(\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}\) \((-1,1)\) \(\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}\) |
|
| الحلول هي\((2,4)\) و\((-1,1)\). |
حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.\).
- إجابة
-
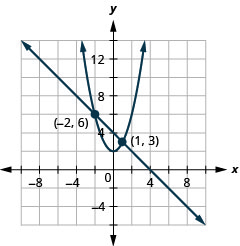
الشكل 11.5.3
حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{x-y=-1} \\ {y=-x^{2}+3}\end{array}\right.\)
- إجابة
-
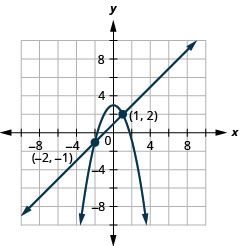
الشكل 11.5.4
لتحديد الرسم البياني لكل معادلة، ضع في اعتبارك خصائص\(x^{2}\)\(y^{2}\) وشروط كل مخروط.
حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.\).
الحل:
| حدد كل رسم بياني. | \(\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.\) |
| ارسم الخيارات الممكنة لتقاطع الدائرة والخط. | 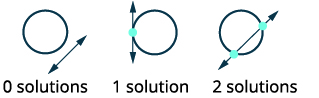 |
|
رسم بياني للدائرة،\((x-2)^{2}+(y+3)^{2}=4\) المركز:\((2,-3)\) دائرة نصف قطرها:\(2\) رسم الخط،\(y=-1\). إنه خط أفقي. |
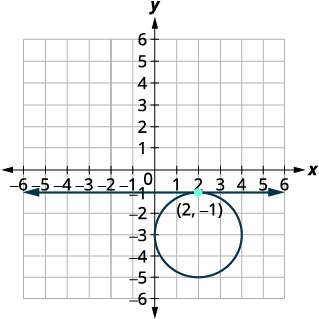 |
| حدد نقاط التقاطع. | يبدو أن نقطة التقاطع هي\((2,-1)\). |
|
تحقق للتأكد من أن الحل يجعل كلتا المعادلتين صحيحتين. \((2,-1)\) \(\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}\) |
|
| الحل هو\((2,-1)\) |
حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{x=-6} \\ {(x+3)^{2}+(y-1)^{2}=9}\end{array}\right.\)
- إجابة
-
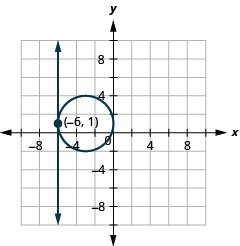
الشكل 11.5.7
حل النظام عن طريق الرسم البياني:\(\left\{\begin{array}{l}{y=4} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.\)
- إجابة
-
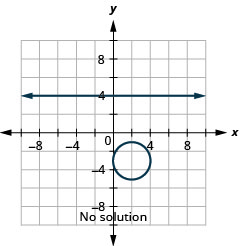
الشكل 11.5.8
حل نظام المعادلات غير الخطية باستخدام التعويض
تعمل طريقة الرسوم البيانية بشكل جيد عندما تكون نقاط التقاطع عبارة عن أعداد صحيحة ويسهل قراءتها من الرسم البياني. ولكن في كثير من الأحيان يكون من الصعب قراءة إحداثيات نقاط التقاطع. طريقة الاستبدال هي طريقة جبرية تعمل بشكل جيد في العديد من المواقف. إنه يعمل بشكل جيد بشكل خاص عندما يكون من السهل حل إحدى المعادلات لأحد المتغيرات.
طريقة الاستبدال تشبه إلى حد كبير طريقة الاستبدال التي استخدمناها لأنظمة المعادلات الخطية. يتم سرد الخطوات أدناه كمرجع.
حل نظام المعادلات غير الخطية بالتعويض
- حدد الرسم البياني لكل معادلة. ارسم الخيارات الممكنة للتقاطع.
- حل إحدى المعادلات لأي متغير.
- استبدل التعبير من الخطوة 2 بالمعادلة الأخرى.
- حل المعادلة الناتجة.
- استبدل كل حل في الخطوة 4 بإحدى المعادلات الأصلية للعثور على المتغير الآخر.
- اكتب كل حل كزوج مطلوب.
- تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين.
حل النظام باستخدام الاستبدال:\(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right.\)
الحل:
| حدد كل رسم بياني. | \(\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.\) |
| ارسم الخيارات الممكنة لتقاطع القطع الناقص والخط. |  |
| تم حل\(y=3x-3\) المعادلة لـ\(y\). |  |
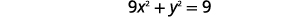 |
|
| استبدل\(3x-3\)\(y\) في المعادلة الأولى. |  |
| حل المعادلة لـ\(x\). | 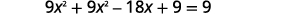 |
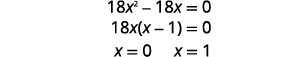 |
|
| استبدل\(x=0\)\(x=1\) وابحث\(y=3x-3\) عن\(y\) -. |  |
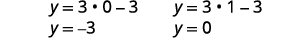 |
|
| الأزواج المرتبة هي\((0,-3), (1,0)\). | |
|
تحقق من كلا الزوجين المرتبين في كلتا المعادلتين. \((0,-3)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}\) \((1,0)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}\) |
|
| الحلول هي\((0,-3), (1,0)\). |
حل النظام باستخدام الاستبدال:\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {y=\frac{1}{3} x-3}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل النظام باستخدام الاستبدال:\(\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=x+2}\end{array}\right.\)
- إجابة
-
\(\left(-\frac{4}{5}, \frac{6}{5}\right),(0,2)\)
حتى الآن، يحتوي كل نظام من المعادلات غير الخطية على حل واحد على الأقل. سيعرض المثال التالي خيارًا آخر.
حل النظام باستخدام الاستبدال:\(\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=x-2}\end{array}\right.\)
الحل:
| حدد كل رسم بياني. | \(\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.\) |
| ارسم الخيارات الممكنة لتقاطع القطع المكافئ والخط. | 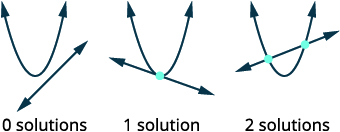 |
| تم حل\(y=x-2\) المعادلة لـ\(y\). | 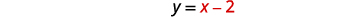 |
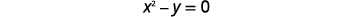 |
|
| استبدل\(x-2\)\(y\) في المعادلة الأولى. |  |
| حل المعادلة لـ\(x\). |  |
| هذا لا يؤثر بسهولة، لذلك يمكننا التحقق من التمييز. | |
| \(\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}\) |
التمييز سلبي، لذلك لا يوجد حل حقيقي. لا يوجد حل للنظام. |
حل النظام باستخدام الاستبدال:\(\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=2 x-3}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل النظام باستخدام الاستبدال:\(\left\{\begin{array}{l}{y^{2}-x=0} \\ {y=3 x-2}\end{array}\right.\)
- إجابة
-
\(\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)\)
حل نظام المعادلات غير الخطية باستخدام الحذف
عندما درسنا أنظمة المعادلات الخطية، استخدمنا طريقة الحذف لحل النظام. يمكننا أيضًا استخدام الحذف لحل أنظمة المعادلات غير الخطية. يعمل بشكل جيد عندما تحتوي المعادلات على كلا المتغيرين بشكل مربع. عند استخدام الحذف، نحاول جعل معاملات متغير واحد أضداد، لذلك عندما نجمع المعادلات معًا، يتم حذف هذا المتغير.
طريقة الحذف تشبه إلى حد كبير طريقة الحذف التي استخدمناها لأنظمة المعادلات الخطية. يتم سرد الخطوات كمرجع.
حل نظام المعادلات بالحذف
- حدد الرسم البياني لكل معادلة. ارسم الخيارات الممكنة للتقاطع.
- اكتب المعادلتين في الصورة القياسية.
- قم بعمل معاملات أضداد متغير واحد.
حدد المتغير الذي ستقوم بإزالته.
اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد. - أضف المعادلات الناتجة من الخطوة 3 لإزالة متغير واحد.
- حل للمتغير المتبقي.
- استبدل كل حل من الخطوة 5 بإحدى المعادلات الأصلية. ثم قم بحل المتغير الآخر.
- اكتب كل حل كزوج مطلوب.
- تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين.
حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=4}\end{array}\right.\)
الحل:
| حدد كل رسم بياني. | 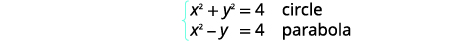 |
| ارسم الخيارات الممكنة لتقاطع الدائرة والقطع المكافئ. | 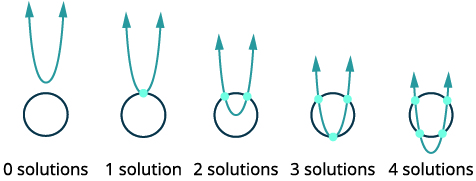 |
| كلا المعادلتين في الشكل القياسي. | 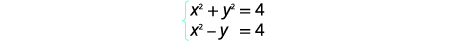 |
| للحصول على معاملات عكسية لـ\(x^{2}\)، سنضرب المعادلة الثانية في\(-1\). | 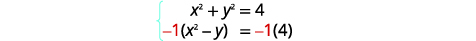 |
| قم بالتبسيط. | 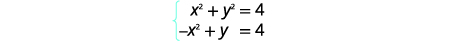 |
| أضف المعادلتين لإزالة\(x^{2}\)/ | 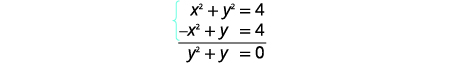 |
| حل لـ\(y\). | 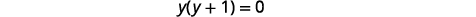 |
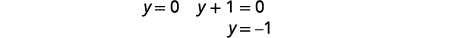 |
|
| استبدل\(y=0\)\(y=-1\) وفي إحدى المعادلات الأصلية. ثم قم بحل المشكلة\(x\). | 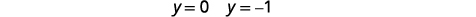 |
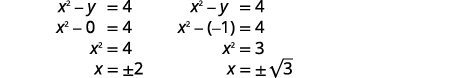 |
|
| اكتب كل حل كزوج مطلوب. | الأزواج المرتبة هي\((-2,0)(2,0)\). \((\sqrt{3},-1)(-\sqrt{3},-1)\) |
| تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين. | |
| سنترك الشيكات لكل حل من الحلول الأربعة لك. | الحلول هي\((-2,0),(2,0),(\sqrt{3},-1)\)، و\((-\sqrt{3},-1)\). |
حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right.\)
- إجابة
-
\((-3,0),(3,0),(-2 \sqrt{2},-1),(2 \sqrt{2},-1)\)
حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {-x+y^{2}=1}\end{array}\right.\)
- إجابة
-
\((-1,0),(0,1),(0,-1)\)
هناك أيضًا أربعة خيارات عندما نفكر في الدائرة والهايبربولا.
حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
الحل:
| حدد كل رسم بياني. | \(\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.\) |
| ارسم الخيارات الممكنة لتقاطع الدائرة والهايبربولا. | 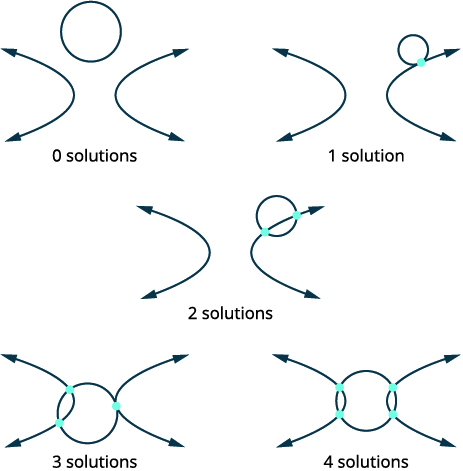 |
| كلا المعادلتين في الشكل القياسي. | \(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\) |
| معاملات\(y^{2}\) معاكسة، لذلك سنضيف المعادلات. |
\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\) \(2 x^{2}=8\) |
| قم بالتبسيط. | \(x^{2}=4\) \(x=\pm 2\) \(x=2 \quad x=-2\) |
| استبدل\(x=2\)\(x=-2\) وفي إحدى المعادلات الأصلية. ثم قم بحل المشكلة\(y\). | \(\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}\) |
| اكتب كل حل كزوج مطلوب. | الأزواج المرتبة هي\((-2, \sqrt{3}),(-2,-\sqrt{3})\)،\((2, \sqrt{3}),\) و\((2,-\sqrt{3})\). |
| تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين. | |
| سنترك الشيكات لكل حل من الحلول الأربعة لك. | الحلول هي\((-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})\)، و\((2,-\sqrt{3})\). |
حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y^{2}-x^{2}=7}\end{array}\right.\)
- إجابة
-
\((-3,-4),(-3,4),(3,-4),(3,4)\)
حل النظام عن طريق الإزالة:\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y^{2}=4}\end{array}\right.\)
- إجابة
-
\((-2,0),(2,0)\)
استخدم نظام المعادلات غير الخطية لحل التطبيقات
يمكن استخدام أنظمة المعادلات غير الخطية لنمذجة العديد من التطبيقات وحلها. سننظر إلى الوضع الهندسي اليومي كمثال لنا.
الفرق بين مربعي الرقمين هو\(15\). مجموع الأرقام هو\(5\). ابحث عن الأرقام.
الحل:
| حدد ما نبحث عنه. | رقمان مختلفان. |
| حدد المتغيرات. |
\(x\)= الرقم الأول \(y\)= الرقم الثاني |
| ترجم المعلومات إلى نظام معادلات. | |
| الجملة الأولى. | الفرق بين مربعي الرقمين هو\(15\). |
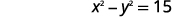 |
|
| الجملة الثانية. | مجموع الأرقام هو\(5\). |
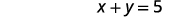 |
|
| حل النظام عن طريق الاستبدال. | 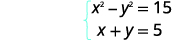 |
| حل المعادلة الثانية لـ\(x\). |  |
| استبدل\(x\) المعادلة الأولى. | 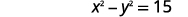 |
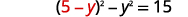 |
|
| قم بالتوسع والتبسيط. | 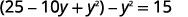 |
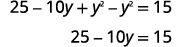 |
|
| حل لـ\(y\). | 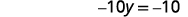 |
 |
|
| استبدل مرة أخرى بالمعادلة الثانية. | 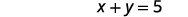 |
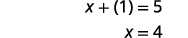 |
|
| الأرقام هي\(1\) و\(4\). |
الفرق بين مربعي الرقمين هو\(−20\). مجموع الأرقام هو\(10\). ابحث عن الأرقام.
- إجابة
-
\(4\)و\(6\)
الفرق بين مربعي الرقمين هو\(35\). مجموع الأرقام هو\(−1\). ابحث عن الأرقام.
- إجابة
-
\(-18\)و\(17\)
اشترت ميرا تلفزيونًا\(25\) «صغيرًا» لمطبخها. يتم قياس حجم التلفزيون على قطر الشاشة. تحتوي الشاشة أيضًا على مساحة بوصة\(300\) مربعة. ما طول شاشة التلفزيون وعرضها؟
الحل:
| حدد ما نبحث عنه. | طول المستطيل وعرضه. |
| حدد المتغيرات. |
Let\(x\) = عرض المستطيل \(y\)= طول المستطيل |
| ارسم مخططًا للمساعدة في تصور الموقف. | 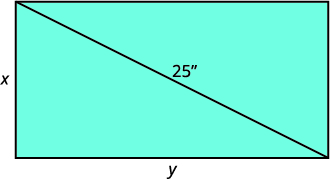 |
| المساحة هي بوصة\(300\) مربعة. | |
| ترجم المعلومات إلى نظام معادلات. | قطر المثلث الأيمن هو\(25\) بوصة. |
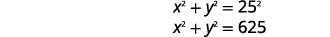 |
|
| مساحة المستطيل هي بوصة\(300\) مربعة. | |
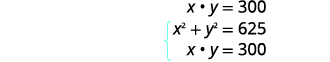 |
|
| حل النظام باستخدام الاستبدال. |  |
| حل المعادلة الثانية لـ\(x\). |  |
| استبدل\(x\) المعادلة الأولى. | 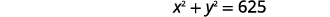 |
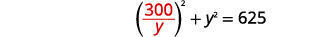 |
|
| قم بالتبسيط. | 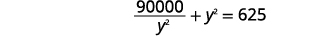 |
| اضرب\(y^{2}\) في لمسح الكسور. | 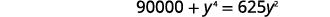 |
| ضع في النموذج القياسي. | 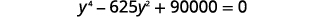 |
| حل عن طريق التخصيم | 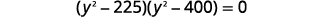 |
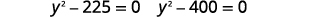 |
|
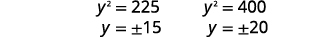 |
|
| \(y\)نظرًا لوجود جانب من المستطيل، فإننا نتجاهل القيم السالبة. |  |
| استبدل مرة أخرى بالمعادلة الثانية. | 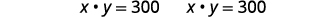 |
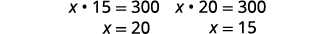 |
|
| إذا كان الطول\(15\) بالبوصة، يكون العرض\(20\) بوصات. | |
| إذا كان الطول\(20\) بالبوصة، يكون العرض\(15\) بوصات. |
اشترى إدغار جهاز تلفزيون\(20\) «صغير» لمرآبه. يتم قياس حجم التلفزيون على قطر الشاشة. تحتوي الشاشة أيضًا على مساحة بوصة\(192\) مربعة. ما طول شاشة التلفزيون وعرضها؟
- إجابة
-
إذا كان الطول\(12\) بالبوصة، يكون العرض\(16\) بوصات. إذا كان الطول\(16\) بالبوصة، يكون العرض\(12\) بوصات.
اشترت عائلة Harper ميكروفونًا صغيرًا لغرفتها العائلية. قطر الباب يقيس\(15\) بوصة. تبلغ مساحة الباب أيضًا بوصات\(108\) مربعة. ما هو طول وعرض باب الميكروويف؟
- إجابة
-
إذا كان الطول\(12\) بالبوصة، يكون العرض\(9\) بوصات. إذا كان الطول\(9\) بالبوصة، يكون العرض\(12\) بوصات.
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل المعادلات غير الخطية.
- أنظمة المعادلات غير الخطية
- حل نظام المعادلات غير الخطية
- حل نظام المعادلات غير الخطية بالحذف
- نظام المعادلات غير الخطية - تطبيقات المساحة والمحيط
المفاهيم الرئيسية
- كيفية حل نظام المعادلات غير الخطية بالرسم البياني.
- حدد الرسم البياني لكل معادلة. ارسم الخيارات الممكنة للتقاطع.
- ارسم المعادلة الأولى بيانيًا.
- ارسم المعادلة الثانية على نفس نظام الإحداثيات المستطيلة.
- حدد ما إذا كانت الرسوم البيانية تتقاطع.
- حدد نقاط التقاطع.
- تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين.
- كيفية حل نظام المعادلات غير الخطية عن طريق الاستبدال.
- حدد الرسم البياني لكل معادلة. ارسم الخيارات الممكنة للتقاطع.
- حل إحدى المعادلات لأي متغير.
- استبدل التعبير من الخطوة 2 بالمعادلة الأخرى.
- حل المعادلة الناتجة.
- استبدل كل حل في الخطوة 4 بإحدى المعادلات الأصلية للعثور على المتغير الآخر.
- اكتب كل حل كزوج مطلوب.
- تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين.
- كيفية حل نظام المعادلات بالحذف.
- حدد الرسم البياني لكل معادلة. ارسم الخيارات الممكنة للتقاطع.
- اكتب المعادلتين في الصورة القياسية.
- قم بعمل معاملات أضداد متغير واحد.
حدد المتغير الذي ستقوم بإزالته.
اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد. - أضف المعادلات الناتجة من الخطوة 3 لإزالة متغير واحد.
- حل للمتغير المتبقي.
- استبدل كل حل من الخطوة 5 بإحدى المعادلات الأصلية. ثم قم بحل المتغير الآخر.
- اكتب كل حل كزوج مطلوب.
- تأكد من أن كل زوج مرتب هو حل لكل من المعادلتين الأصليتين.


