Skip to main content
Global

11.5: الغلو

  1. Last updated
  2. Save as PDF
  • Page ID
    201796

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • رسم بياني لحالة هيبربولا مع مركزها في\((0,0)\)
    • رسم بياني لحالة هيبربولا مع مركزها في\((h,k)\)
    • حدد المقاطع المخروطية من خلال معادلاتها

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. حل:\(x^{2}=12\).
      إذا فاتتك هذه المشكلة، راجع المثال 9.1.
    2. قم بالتوسع:\((x−4)^{2}\).
      إذا فاتتك هذه المشكلة، راجع مثال 5.32.
    3. رسم بياني\(y=-\frac{2}{3} x\).
      إذا فاتتك هذه المشكلة، راجع المثال 3.4.

    رسم بياني لهايبربولا مع المركز في\((0,0)\)

    يُطلق على القسم المخروطي الأخير الذي سننظر إليه اسم hyperbola. سنرى أن معادلة الهيبربولا تبدو مثل معادلة القطع الناقص، إلا أنها فرق وليس مجموع. في حين أن معادلات القطع الناقص والمفرط متشابهة جدًا، إلا أن رسوماتها البيانية مختلفة جدًا.

    نُعرّف الهيبربولا بأنها جميع النقاط في المستوى حيث يكون الفرق بين مسافاتها ونقطتين ثابتتين ثابتًا. كل نقطة من النقاط الثابتة تسمى محور الهايبربولا.

    تعريف\(\PageIndex{1}\)

    الهيبربولا هي جميع النقاط في المستوى حيث يكون فرق المسافات بين نقطتين ثابتتين ثابتًا. كل نقطة من النقاط الثابتة تسمى محور الهايبربولا.

    يوضِّح الشكل مخروطًا دائريًا قائمًا مزدوجًا مقطوعًا إلى شرائح من مستوى موازٍ للمحور الرأسي للمخروط الذي يُشكِّل هيبربولا. تم تسمية هذا الرقم بـ «€ hyperbola※™.
    الشكل 11.4.1

    ويسمى الخط الذي يمر عبر البؤر بالمحور المستعرض. النقطتان اللتان يتقاطع فيهما المحور المستعرض مع الهايبربولا هما كل منهما قمة رأس الهايبربولا. يُطلق على نقطة الوسط في الجزء الذي ينضم إلى البؤر اسم مركز الهيبربولا. يُطلق على الخط العمودي على المحور المستعرض الذي يمر عبر المركز اسم المحور المترافق. يُطلق على كل جزء من الرسم البياني اسم فرع الهايبربولا.

    يوضِّح الشكل رسمين بيانيين للهايبربولا. يُظهر الرسم البياني الأول المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. تظهر الرؤوس والبؤر بنقاط تقع على المحور المستعرض، وهو المحور السيني. تمر الفروع عبر القمم وتفتح يمينًا ويسارًا. المحور y هو المحور المترافق. يُظهر الرسم البياني الثاني المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. تظهر الرؤوس والبؤر بالنقاط التي تقع على المحور العرضي، وهو المحور y. تمر الفروع عبر الرؤوس وتفتح لأعلى ولأسفل. المحور السيني هو المحور المترافق.
    الشكل 11.4.2

    مرة أخرى هدفنا هو ربط هندسة المخروط بالجبر. يمنحنا وضع hyperbola على نظام إحداثيات مستطيل هذه الفرصة. في الشكل، وضعنا الهايبربولا بحيث\(((−c,0),(c,0))\) تكون البؤر على\(x\) المحور السيني والمركز هو الأصل.

    يوضِّح الشكل الرسم البياني للهايبربولا. يُظهر الرسم البياني المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. يتم تمييز البؤر (سالبة c، 0) و (c، 0) بنقطة وتقع على المحور السيني. يتم تمييز الرؤوس بنقطة وتقع على المحور السيني. تمر الفروع عبر القمم وتفتح يمينًا ويسارًا. يتم وضع علامة d suber 1 على المسافة من (سالب c، 0) إلى نقطة على الفرع (x، y). يتم وضع علامة d sub 2 على المسافة من (x، y) على الفرع إلى (c، 0).
    الشكل 11.4.3

    يوضح التعريف أن فرق المسافة من البؤر إلى النقطة\((x,y)\) ثابت. \(|d_{1}−d_{2}|\)هذا هو الثابت الذي سنسميه\(2a\) كذلك\(|d_{1}-d_{2} |=2 a\). سنستخدم صيغة المسافة لتقودنا إلى صيغة جبرية للقطع الناقص.

    \(\left|d_{1} - d_{2}\right| =2 a\)

    استخدم صيغة المسافة للبحث\(d_{1}, d_{2}\)

    \(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)

    القضاء على الجذور. لتبسيط معادلة القطع الناقص، نسمح بذلك\(c^{2}-a^{2}=b^{2}\).

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)

    لذا، فإن معادلة الهيبربولا المتمركزة عند الأصل في الشكل القياسي هي:

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)

    لرسم بياني للهايبربولا، سيكون من المفيد معرفة عمليات الاعتراض. سنجد\(x\) -Intercepts و\(y\) -Intercepts باستخدام الصيغة.

    \(x\)- عمليات الاعتراض

    دعونا\(y=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)

    \(x\)عمليات الاعتراض - هي\((a,0)\) و\((−a,0)\).

    \(y\)- عمليات الاعتراض

    دعونا\(x=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)

    لا توجد\(y\) عمليات اعتراض.

    تساعدنا\(a, b\) القيم في المعادلة أيضًا في إيجاد خطوط التقارب للهايبربولا. خطوط التقارب عبارة عن خطوط مستقيمة تتقاطع معها فروع الرسم البياني ولكنها لا تتقاطع أبدًا عندما تصبح\(x, y\) القيم أكبر وأكبر.

    للعثور على خطوط التقارب، نرسم مستطيلًا تتقاطع أضلاعه مع المحور x عند الرؤوس\((−a,0),(a,0)\)، ويتقاطع\(y\) المحور السيني عند\((0,−b), (0,b)\). والخطوط التي تحتوي على أقطار هذا المستطيل هي خطوط التقارب للهايبربولا. لا يشكل المستطيل وخطوط التقارب جزءًا من الضخامة، ولكنها تساعدنا في رسم الهيبربولا بيانيًا.

    يوضِّح الشكل الرسم البياني للهايبربولا. يُظهر الرسم البياني المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. الرؤوس هي (سالب a، 0) و (a، 0) ويتم تمييزها بنقطة وتقع على المحور x. تقع النقاط (0، ب) و (0، سالب) على المحور y. يوجد مستطيل مركزي تتقاطع أضلاعه مع المحور السيني عند الرؤوس (سالب a، 0) و (a، 0) ويتقاطع مع المحور y عند (0، b) و (0، سالب b). تُعطى خطوط التقارب بـ y وهي تساوي b مقسومًا على a مضروبًا في x و y يساوي سالب b مقسومًا على a في x ويتم رسمها كأقطار المستطيل المركزي. تمر فروع الهيبربولا عبر الرؤوس وتفتح يمينًا ويسارًا وتقترب من خطوط التقارب.
    الشكل 11.4.4

    تمر خطوط التقارب عبر نقطة الأصل ويمكننا تقييم ميلها باستخدام المستطيل الذي رسمناه. لديهم معادلات\(y=\frac{b}{a} x\) و\(y=-\frac{b}{a} x\).

    توجد معادلتان للمبالغ الزائدة، اعتمادًا على ما إذا كان المحور المستعرض رأسيًا أم أفقيًا. يمكننا معرفة ما إذا كان المحور العرضي أفقيًا من خلال النظر إلى المعادلة. عندما تكون المعادلة في الشكل القياسي، إذا كان الحد\(x^{2}\) -موجبًا، يكون المحور العرضي أفقيًا. عندما تكون المعادلة في الشكل القياسي، إذا كان الحد\(y^{2}\) -موجبًا، يكون المحور العرضي رأسيًا.

    يمكن اشتقاق المعادلات الثانية بشكل مشابه لما قمنا به. سنلخص النتائج هنا.

    تعريف\(\PageIndex{2}\)

    الشكل القياسي لمعادلة هايبربولا مع المركز\((0,0)\)

    الشكل القياسي لمعادلة الهيبربولا مع المركز\((0,0)\) هو

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\)أو\(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)

    يوضِّح الشكل التمثيل البياني لنقطتين زائدتين. يُظهر الرسم البياني الأول المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. الرؤوس هي (سالب a، 0) و (a، 0) ويتم تمييزها بنقطة وتقع على المحور x. تقع النقاط (0، ب) و (0، سالب) على المحور y. يوجد مستطيل مركزي تتقاطع أضلاعه مع المحور السيني عند الرؤوس (سالب a، 0) و (a، 0) ويتقاطع مع المحور y عند (0، b) و (0، سالب b). تُعطى خطوط التقارب بـ y وهي تساوي b مقسومًا على a مضروبًا في x و y يساوي سالب b مقسومًا على a في x ويتم رسمها كأقطار المستطيل المركزي. تمر فروع الهيبربولا عبر الرؤوس وتفتح يمينًا ويسارًا وتقترب من خطوط التقارب. يُظهر الرسم البياني الثاني المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. الرؤوس هي (0، أ) و (0، سالب أ) ويتم تمييزها بنقطة وتقع على المحور y. تقع النقاط (0، ب) و (0، سالب) على المحور y. يوجد مستطيل مركزي تتقاطع أضلاعه مع المحور y عند الرؤوس (0، a) و (0، سالب a) ويتقاطع مع المحور y عند (سالب b، 0) و (b، 0). تمر فروع الهيبربولا عبر الرؤوس وتنفتح لأعلى ولأسفل وتقترب من خطوط التقارب.
    الشكل 11.4.5

    لاحظ أنه، على عكس معادلة القطع الناقص، لا\(x^{2}\) يكون المقام دائمًا\(a^{2}\) وقامه\(y^{2}\) ليس دائمًا\(b^{2}\).

    لاحظ أنه عندما يكون\(x^{2}\) المصطلح -موجبًا، يكون المحور المستعرض على\(x\) المحور -. عندما يكون\(y^{2}\) مصطلح -term موجبًا، يكون المحور المستعرض على\(y\) المحور -.

    الأشكال القياسية لمعادلة هايبربولا مع المركز\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    اتجاه \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">المحور المستعرض على\(x\) المحور -.
    يفتح يمينًا ويسارًا    		 \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">المحور المستعرض على\(y\) المحور -.
    يفتح لأعلى ولأسفل
    رءوس \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    \(x\)- عمليات الاعتراض \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">لا شيء
    \(y\)- عمليات الاعتراض \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">لا شيء \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    المستطيل \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">الاستخدام\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">الاستخدام\((0, \pm a)( \pm b, 0)\)
    خطوط التقارب \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    الجدول 11.4.1

    سنستخدم هذه الخصائص لرسم الضلالات البيانية.

    مثال\(\PageIndex{1}\) How to Graph a Hyperbola with Center \((0,0)\)

    رسم بياني\(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\).

    الحل:

    الخطوة 1: اكتب المعادلة في النموذج القياسي. المعادلة في الشكل القياسي. \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\)
    الخطوة 2: حدد ما إذا كان المحور العرضي أفقيًا أم رأسيًا. نظرًا لأن\(x^{2}\) مصطلح -term إيجابي، يكون المحور المستعرض أفقيًا. المحور العرضي أفقي.
    الخطوة 3: ابحث عن الرؤوس. منذ\(a^{2}=25\) ذلك الحين\(a=\pm 5\). توجد الرؤوس على\(x\) المحور -. \((-5,0),(5,0)\)
    الخطوة 4: ارسم المستطيل المتمركز عند تقاطع الأصل عند أحد المحاور\(\pm a\) والآخر عنده\(\pm b\).

    نظرًا لأن\(a=\pm 5\) المستطيل سيتقاطع مع\(x\) المحور -عند الرؤوس.

    نظرًا لأن\(b=\pm 2\) المستطيل سيتقاطع مع\(y\) المحور -عند\((0,-2)\) و\((0,2)\).

    		 لقطة شاشة (148) .png

    الخطوة 5: ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل.

    		 تحتوي خطوط التقارب على المعادلات\(y=\frac{5}{2} x, y=-\frac{5}{2} x\). لقطة شاشة (149) .png
    الخطوة 6: ارسم فرعين من الهايبربولا. ابدأ من كل قمة واستخدم خطوط التقارب كدليل. 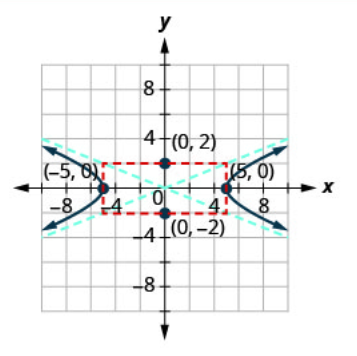لقطة شاشة (150) .png
    الجدول 11-4-2
    التمارين\(\PageIndex{1}\)

    رسم بياني\(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\).

    إجابة
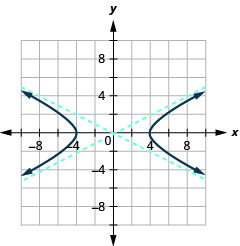
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، حيث تكون خطوط التقارب y تساوي زائد أو ناقص نصف مضروبًا في x، والفروع التي تمر عبر القمم (زائد أو ناقص 4، 0) وتفتح يمينًا ويسارًا.
    الشكل 11.4.9
    التمارين\(\PageIndex{2}\)

    رسم بياني\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\).

    إجابة
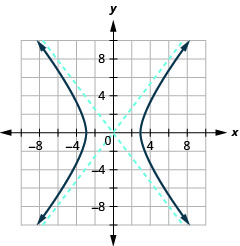
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، حيث تكون خطوط التقارب y تساوي زائد أو ناقص أربعة ثلثي في x، والفروع التي تمر عبر القمم (زائد أو ناقص 3، 0) وتفتح يمينًا ويسارًا.
    الشكل 11.4.10

    نحن نلخص الخطوات كمرجع.

    رسم بياني لهايبربولا المتمركز في\((0,0)\)

    1. اكتب المعادلة في الصورة القياسية.
    2. حدد ما إذا كان المحور العرضي أفقيًا أم رأسيًا.
    3. ابحث عن الرؤوس.
    4. ارسم المستطيل المتمركز عند نقطة الأصل التي تتقاطع مع أحد المحاور عند\(±a\) المحور الآخر\(±b\).
    5. ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل.
    6. ارسم فرعين من الهايبربولا.

    في بعض الأحيان، يجب وضع معادلة hyperbola أولاً في الشكل القياسي قبل رسمها بيانيًا.

    مثال\(\PageIndex{2}\)

    رسم بياني\(4 y^{2}-16 x^{2}=64\).

    الحل:

      \(4 y^{2}-16 x^{2}=64\)
    لكتابة المعادلة في الصورة القياسية، قم بتقسيم كل حد\(64\) على لجعل المعادلة مساوية لـ\(1\). \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\)
    قم بالتبسيط. \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\)
    نظرًا لأن\(y^{2}\) مصطلح -term إيجابي، يكون المحور المستعرض عموديًا. منذ\(a^{2}=16\) ذلك الحين\(a=\pm 4\).  
    توجد الرؤوس على\(y\) المحور -،\((0,-a),(0, a)\). منذ\(b^{2}=4\) ذلك الحين\(b=\pm 2\). \((0,-4),(0,4)\)
    ارسم المستطيل الذي يتقاطع مع\(x\)\(y\) المحور -عند\((-2,0),(2,0)\) والمحور -عند الرؤوس. ارسم خطوط التقارب من خلال أقطار المستطيل. ارسم فرعين من الهايبربولا. .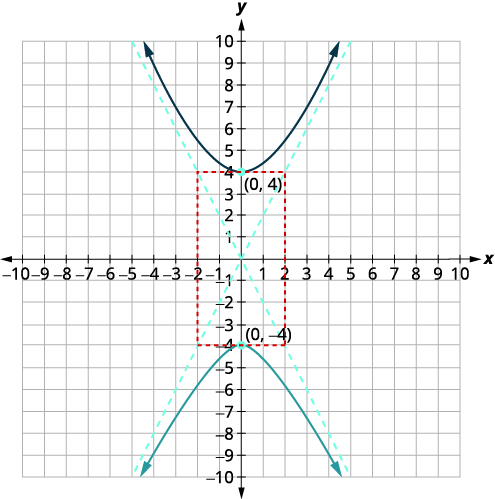
    الجدول 11-4-3
    التمارين\(\PageIndex{3}\)

    رسم بياني\(4 y^{2}-25 x^{2}=100\).

    إجابة
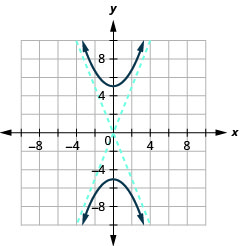
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، حيث تكون خطوط التقارب y تساوي زائد أو ناقص خمسة أنصاف في x، والفروع التي تمر عبر القمم (0، زائد أو ناقص 5) وتفتح لأعلى ولأسفل.
    الشكل 11.4.12
    التمارين\(\PageIndex{4}\)

    رسم بياني\(25 y^{2}-9 x^{2}=225\).

    إجابة
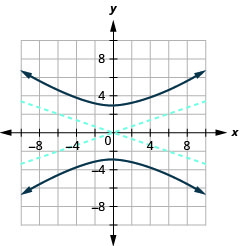
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، حيث تكون خطوط التقارب y تساوي زائد أو ناقص ثلاثة أخماس في x، والفروع التي تمر عبر الرؤوس (0، زائد أو ناقص 3) وتفتح لأعلى ولأسفل.
    الشكل 11.4.13

    رسم بياني لهايبربولا مع المركز في\((h,k)\)

    لا تتمركز Hyperbolas دائمًا في الأصل. عندما تتمركز الهيبربولا\((h,k)\) في المعادلات تتغير قليلاً كما هو موضح في الجدول.

    الأشكال القياسية لمعادلة هايبربولا مع المركز\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    اتجاه \ (frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">المحور المستعرض أفقي. يفتح يمينًا ويسارًا \ (frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">المحور المستعرض عمودي. يفتح لأعلى ولأسفل
    المركز \ (frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2} =1\) ">\((h,k)\) \ (frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">\((h,k)\)
    رءوس \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2} =1\) ">\(a\) الوحدات إلى اليسار واليمين من المركز \ (frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">\(a\) الوحدات فوق المركز وتحته
    المستطيل \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2} =1\) ">استخدم\(a\) الوحدات يسار/يمين\(b\) الوحدات المركزية أعلى/أسفل المركز \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">استخدم\(a\) الوحدات أعلى/أسفل\(b\) وحدات المركز يسار/يمين المركز
    الجدول 11-4-4
    مثال\(\PageIndex{3}\) How to Graph a Hyperbola with Center \((h,k)\)

    رسم بياني\(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)

    الحل:

    الخطوة 1: اكتب المعادلة في النموذج القياسي. المعادلة في الشكل القياسي. \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
    الخطوة 2: حدد ما إذا كان المحور العرضي أفقيًا أم رأسيًا. نظرًا لأن\(x^{2}\) مصطلح -term إيجابي، فإن hyperbola يفتح يسارًا ويمينًا. المحور العرضي أفقي. يفتح الهايبربولا يمينًا ويسارًا.
    الخطوة 3: ابحث عن المركز و\(a, b\). \(h=1\)و\(k=2\)
    \(a^{2}=9\)
    \(b^{2}=16\)

    \(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\)

    المركز:\((1,2)\)

    \(a=3\)

    \(b=4\)
    الخطوة 4: ارسم المستطيل الذي يركز على\((h,k)\) الاستخدام\(a,b\).

    ضع علامة على المركز،\((1,2)\).

    ارسم المستطيل الذي يمر عبر\(3\) وحدات النقاط إلى يسار/يمين المركز\(4\) والوحدات فوق المركز وأسفله.

    		 لقطة شاشة (151) .png
    الخطوة 5: ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل. ضع علامة على الرؤوس. ارسم الأقطار. حدد الرؤوس الموجودة على\(3\) وحدات المستطيل على يسار ويمين المركز. لقطة شاشة (152) .png
    الخطوة 6: ارسم فرعين من الهايبربولا. ابدأ من كل قمة واستخدم خطوط التقارب كدليل. لقطة شاشة (153) .png
    الجدول 11-4-5
    التمارين\(\PageIndex{5}\)

    رسم بياني\(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\).

    إجابة
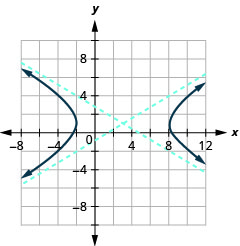
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، مع وجود خط تقارب يمر عبر (سالب 2، سالب 2) و (8، 4) وخط التقارب الذي يمر عبره (سالب 2، 4) و (8، سالب 2)، والفروع التي تمر عبر القمم ( سلبي 2، 2) و (8، 2) ويفتح يسارًا ويمينًا.
    الشكل 11.4.17
    التمارين\(\PageIndex{6}\)

    رسم بياني\(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\).

    إجابة
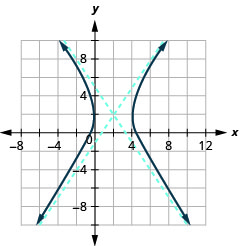
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، مع وجود المركز (2، 2) وخط التقارب الذي يمر عبر (0، سالب 1) و (4، 5) وخط التقارب الذي يمر خلال (0، 5) و (4، سالب 1)، والفروع التي تمر عبر القمم (0، 2) و (4، 2) ويفتح يسارًا ويمينًا.
    الشكل 11.4.18

    نحن نلخص الخطوات للرجوع إليها بسهولة.

    رسم بياني لهايبربولا المتمركز في\((h,k)\)

    1. اكتب المعادلة في الصورة القياسية.
    2. حدد ما إذا كان المحور العرضي أفقيًا أم رأسيًا.
    3. ابحث عن المركز و\(a,b\).
    4. ارسم المستطيل الذي يركز على\((h,k)\) الاستخدام\(a,b\).
    5. ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل. ضع علامة على الرؤوس.
    6. ارسم فرعين من الهايبربولا.

    كن حذرًا عند تحديد المركز. تحتوي المعادلة القياسية\(x−h\)\(y−k\) على المركز كـ\((h,k)\).

    مثال\(\PageIndex{4}\)

    رسم بياني\(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\).

    الحل:

      .
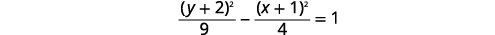    نظرًا لأن\(y^{2}\) مصطلح -term إيجابي، فإن الهايبربولا ينفتح صعودًا وهبوطًا. .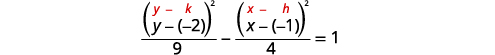
    ابحث عن المركز،\((h,k)\). المركز:\((-1,-2)\)
    ابحث\(a,b\). \(a=3 b=2\)
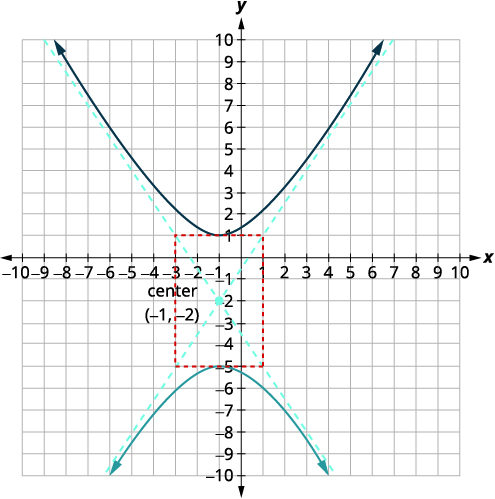
    ارسم المستطيل الذي يمر عبر\(3\) وحدات النقاط فوق المركز وأسفله
    \(2\) والوحدات على يسار/يمين المركز.
    ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل.
    ضع علامة على الرؤوس.
    رسم بياني للفروع.    		 .
    الجدول 11-4-6
    التمارين\(\PageIndex{7}\)

    رسم بياني\(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\).

    إجابة
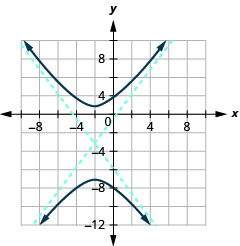
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، بحيث يكون المركز عند (سالب 2، سالب 3)، وخط التقارب الذي يمر خلال (سالب 5، سالب 7) و (1، 1) وخط التقارب الذي يمر خلال (سالب 5، 1) و (1، 7)، والفروع التي تمر عبر القمم (سالب 2، 1) و (سالب 2، سالب 7) وتفتح لأعلى ولأسفل.
    الشكل 11.4.22
    التمارين\(\PageIndex{8}\)

    رسم بياني\(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\).

    إجابة
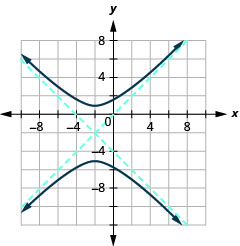
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، بحيث يكون المركز عند (سالب 2، سالب 2)، وخط التقارب الذي يمر خلال (سالب 5، سالب 5) و (1، 1) وخط التقارب الذي يمر عبره (سالب 5، 1) و (1، سالب 5)، و الفروع التي تمر عبر القمم (سالبة 2، 1) و (سالبة 2، سالبة 5) وتفتح لأعلى ولأسفل.
    الشكل 11.4.23

    مرة أخرى، في بعض الأحيان يتعين علينا وضع المعادلة في شكل قياسي كخطوة أولى.

    مثال\(\PageIndex{5}\)

    اكتب المعادلة في الصورة القياسية والرسم البياني\(4 x^{2}-9 y^{2}-24 x-36 y-36=0\).

    الحل:

      .
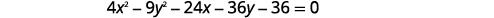    للوصول إلى النموذج القياسي، أكمل المربعات. .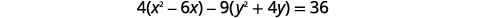
      .
      .
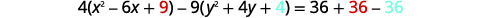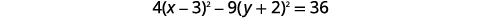    قسّم كل مصطلح\(36\) للحصول على الثابت\(1\). .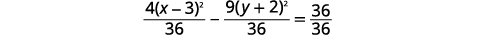
      .
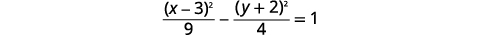    نظرًا لأن\(x^{2}\) مصطلح -term إيجابي، فإن hyperbola يفتح يسارًا ويمينًا.  
    ابحث عن المركز،\((h,k)\). المركز:\((3, -2)\)
    ابحث\(a,b\).

    \(a=3\)

    \(b=4\)
    ارسم المستطيل الذي يمر عبر\(3\) وحدات النقاط إلى يسار/يمين المركز\(2\) والوحدات فوق المركز وأسفله.
    ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل.
    ضع علامة على الرؤوس.
    رسم بياني للفروع.    		 .
    الجدول 11-4-7
    التمارين\(\PageIndex{9}\)
    1. اكتب المعادلة في الصورة القياسية و
    2. رسم بياني\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\).
    إجابة
    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
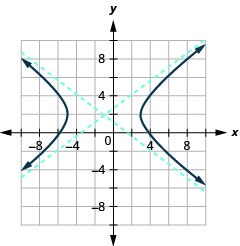
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، مع وجود المركز (سالب 1، 2) وخط التقارب الذي يمر عبره (سالب 5، 5) و (3، سالب 1) وخط التقارب الذي يمر خلال (3، 5) و (سالب 5، سالب 1)، والفروع التي تمر عبر القمم (سالبة 5، 2) و (3، 2) وتفتح يسارًا ويمينًا.
    الشكل 11.4.31
    التمارين\(\PageIndex{10}\)
    1. اكتب المعادلة في الصورة القياسية و
    2. رسم بياني\(16 x^{2}-25 y^{2}+96 x-50 y-281=0\).
    إجابة
    1. \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
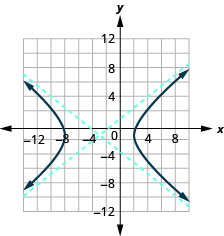
    يوضِّح الرسم البياني المحور السيني والمحور الصادي اللذين يجريان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة، مع وجود المركز (سالب 3، سالب 1) وخط التقارب الذي يمر عبره (سالب 8، سالب 5) و (2، 3) وخط التقارب الذي يمر عبره (سالب 8، 3) و (2، سالب 5)، و الفروع التي تمر عبر القمم (سالب 8، سالب 1) و (2، سالب 1) وتفتح يسارًا ويمينًا.
    الشكل 11.4.32

    تحديد المقاطع المخروطية من خلال معادلاتها

    الآن بعد أن أكملنا دراستنا للأقسام المخروطية، سنلقي نظرة على المعادلات المختلفة ونتعرف على بعض الطرق لتحديد المخروط من خلال معادلته. عندما نحصل على معادلة للرسم البياني، فمن المفيد تحديد المخروط حتى نعرف الخطوات التالية التي يجب اتخاذها.

    لتحديد المخروط من معادلته، يكون من الأسهل أن نضع شروط المتغير على أحد طرفي المعادلة والثوابت على الجانب الآخر.

    مخروطي خصائص\(x^{2}\)\(y^{2}\) - والمصطلحات مثال
    بارابولا \ (x^ {2}\) - و\(y^{2}\) - الشروط">إما\(x^{2}\) أو\(y^{2}\). متغير واحد فقط هو مربع. \(x=3 y^{2}-2 y+1\)
    دائرة \ (x^ {2}\) - و\(y^{2}\) -terms>\(x^{2}\)\(y^{2}\) - و - المصطلحات لها نفس المعاملات. \(x^{2}+y^{2}=49\)
    الشكل البيضاوي \ (x^ {2}\) - و\(y^{2}\) -terms>\(x^{2}\)\(y^{2}\) - و - المصطلحات لها نفس العلامة ومعاملات مختلفة. \(4 x^{2}+25 y^{2}=100\)
    هايبربولا \ (x^ {2}\) - و\(y^{2}\) -terms>\(x^{2}\)\(y^{2}\) - و - المصطلحات لها علامات مختلفة ومعاملات مختلفة. \(25 y^{2}-4 x^{2}=100\)
    الجدول 11-4-8
    مثال\(\PageIndex{6}\)

    حدد الرسم البياني لكل معادلة في صورة دائرة أو مكافئ أو شكل بيضاوي أو هايبربولا.

    1. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    2. \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
    3. \(x^{2}+y^{2}-6 x-8 y=0\)
    4. \(y=-2 x^{2}-4 x-5\)

    الحل:

    أ-\(x^{2}\) المصطلحان\(y^{2}\) - و - لهما نفس العلامة ومعاملات مختلفة.

    \(9 x^{2}+4 y^{2}+56 y+160=0\)

    الشكل البيضاوي

    ب-\(y^{2}\) للمصطلحات\(x^{2}\) - و - علامات مختلفة ومعاملات مختلفة.

    \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)

    هايبربولا

    ج-\(x^{2}\) المصطلحان\(y^{2}\) - و - لهما نفس المعاملات.

    \(x^{2}+y^{2}-6 x-8 y=0\)

    دائرة

    d. متغير واحد فقط\(x\)،، هو مربع.

    \(y=-2 x^{2}-4 x-5\)

    بارابولا

    التمارين\(\PageIndex{11}\)

    حدد الرسم البياني لكل معادلة في صورة دائرة أو مكافئ أو شكل بيضاوي أو هايبربولا.

    1. \(x^{2}+y^{2}-8 x-6 y=0\)
    2. \(4 x^{2}+25 y^{2}=100\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(16 y^{2}-9 x^{2}=144\)
    إجابة
    1. دائرة
    2. الشكل البيضاوي
    3. بارابولا
    4. هايبربولا
    التمارين\(\PageIndex{12}\)

    حدد الرسم البياني لكل معادلة في صورة دائرة أو مكافئ أو شكل بيضاوي أو هايبربولا.

    1. \(16 x^{2}+9 y^{2}=144\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(x^{2}+y^{2}+2 x+6 y+9=0\)
    4. \(4 x^{2}-16 y^{2}=64\)
    إجابة
    1. الشكل البيضاوي
    2. بارابولا
    3. دائرة
    4. هايبربولا

    يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على إرشادات وممارسة إضافية باستخدام hyperbolas.

    • رسم بياني لهايبربولا مع المركز في الأصل
    • رسم بياني لهايبربولا مع المركز ليس في الأصل
    • رسم بياني لـ Hyperbola في شكل عام
    • تحديد الأقسام المخروطية بشكل عام

    المفاهيم الرئيسية

    • Hyperbola: hyperbola هي جميع النقاط في المستوى حيث يكون الفرق بين مسافاتها ونقطتين ثابتتين ثابتًا.
    يوضِّح الشكل مخروطًا دائريًا قائمًا مزدوجًا مقطوعًا إلى شرائح من مستوى موازٍ للمحور الرأسي للمخروط الذي يُشكِّل هيبربولا. يُطلق على الشكل اسم «hyperbola».
    الشكل 11.4.1
    • كل نقطة من النقاط الثابتة تسمى محور الهايبربولا.
      ويسمى الخط الذي يمر عبر البؤر بالمحور المستعرض.
      النقطتان اللتان يتقاطع فيهما المحور المستعرض مع الهايبربولا هما كل منهما قمة رأس الهايبربولا.
      يُطلق على نقطة الوسط في الجزء الذي ينضم إلى البؤر اسم مركز الهيبربولا.
      يُطلق على الخط العمودي على المحور المستعرض الذي يمر عبر المركز اسم المحور المترافق.
      يُطلق على كل جزء من الرسم البياني اسم فرع من الهايبربولا.
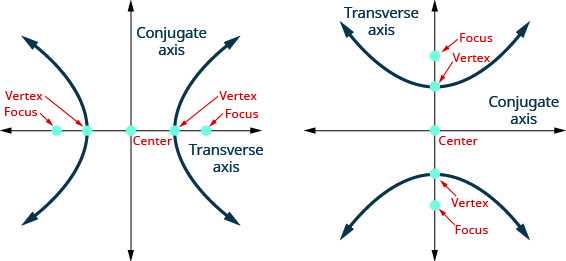
      يوضِّح الشكل رسمين بيانيين للهايبربولا. يُظهر الرسم البياني الأول المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. تظهر الرؤوس والبؤر بنقاط تقع على المحور المستعرض، وهو المحور السيني. تمر الفروع عبر القمم وتفتح يمينًا ويسارًا. المحور y هو المحور المترافق. يُظهر الرسم البياني الثاني المحور x والمحور y اللذين يعملان في الاتجاهين السالب والإيجابي، ولكن على فترات غير مسماة. مركز الهايبربولا هو الأصل. تظهر الرؤوس والبؤر بالنقاط التي تقع على المحور العرضي، وهو المحور y. تمر الفروع عبر الرؤوس وتفتح لأعلى ولأسفل. المحور السيني هو المحور المترافق.

    الشكل 11.4.2

    الأشكال القياسية لمعادلة هايبربولا مع المركز\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    اتجاه \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">المحور المستعرض على\(x\) المحور -.
    يفتح يمينًا ويسارًا    		 \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">المحور المستعرض على\(y\) المحور -.
    يفتح لأعلى ولأسفل
    رءوس \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    \(x\)- عمليات الاعتراض \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">لا شيء
    \(y\)- عمليات الاعتراض \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">لا شيء \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    المستطيل \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">الاستخدام\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">الاستخدام\((0, \pm a)( \pm b, 0)\)
    خطوط التقارب \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    الجدول 11.4.1
    • كيفية رسم بياني لفرط الإيبولا المتمركز في\((0,0)\).
      1. اكتب المعادلة في الصورة القياسية.
      2. حدد ما إذا كان المحور العرضي أفقيًا أم رأسيًا.
      3. ابحث عن الرؤوس.
      4. ارسم المستطيل المتمركز عند نقطة الأصل التي تتقاطع مع أحد المحاور عند\(±a\) المحور الآخر\(±b\).
      5. ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل.
      6. ارسم فرعين من الهايبربولا.

    الأشكال القياسية لمعادلة هايبربولا مع المركز\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    اتجاه \ (frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">المحور المستعرض أفقي. يفتح يمينًا ويسارًا \ (frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">المحور المستعرض عمودي. يفتح لأعلى ولأسفل
    المركز \ (frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2} =1\) ">\((h,k)\) \ (frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">\((h,k)\)
    رءوس \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2} =1\) ">\(a\) الوحدات إلى اليسار واليمين من المركز \ (frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">\(a\) الوحدات فوق المركز وتحته
    المستطيل \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2} =1\) ">استخدم\(a\) الوحدات يسار/يمين\(b\) الوحدات المركزية أعلى/أسفل المركز \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2} =1\) ">استخدم\(a\) الوحدات أعلى/أسفل\(b\) وحدات المركز يسار/يمين المركز
    الجدول 11-4-4
    • كيفية رسم بياني لفرط الإيبولا المتمركز في\((h,k)\).
      1. اكتب المعادلة في الصورة القياسية.
      2. حدد ما إذا كان المحور العرضي أفقيًا أم رأسيًا.
      3. ابحث عن المركز و\(a,b\).
      4. ارسم المستطيل الذي يركز على\((h,k)\) الاستخدام\(a,b\).
      5. ارسم خطوط التقارب - الخطوط التي تمر بأقطار المستطيل. ضع علامة على الرؤوس.
      6. ارسم فرعين من الهايبربولا.
    مخروطي خصائص\(x^{2}\)\(y^{2}\) - والمصطلحات مثال
    بارابولا \ (x^ {2}\) - و\(y^{2}\) - الشروط">إما\(x^{2}\) أو\(y^{2}\). متغير واحد فقط هو مربع. \(x=3 y^{2}-2 y+1\)
    دائرة \ (x^ {2}\) - و\(y^{2}\) -terms>\(x^{2}\)\(y^{2}\) - و - المصطلحات لها نفس المعاملات. \(x^{2}+y^{2}=49\)
    الشكل البيضاوي \ (x^ {2}\) - و\(y^{2}\) -terms>\(x^{2}\)\(y^{2}\) - و - المصطلحات لها نفس العلامة ومعاملات مختلفة. \(4 x^{2}+25 y^{2}=100\)
    هايبربولا \ (x^ {2}\) - و\(y^{2}\) -terms>\(x^{2}\)\(y^{2}\) - و - المصطلحات لها علامات مختلفة ومعاملات مختلفة. \(25 y^{2}-4 x^{2}=100\)
    الجدول 11-4-8

    مسرد المصطلحات

    هيبربولا
    يُعرَّف الهايبربولا بأنه جميع النقاط في المستوى حيث يكون فرق المسافات بين نقطتين ثابتتين ثابتًا.