11.4E: تمارين
- Page ID
- 201818
الممارسة تجعلها مثالية
في التمارين التالية، قم برسم بياني لكل شكل بيضاوي.
- \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
- \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
- \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
- \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
- \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
- \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
- \(x^{2}+\frac{y^{2}}{4}=1\)
- \(\frac{x^{2}}{9}+y^{2}=1\)
- \(4 x^{2}+25 y^{2}=100\)
- \(16 x^{2}+9 y^{2}=144\)
- \(16 x^{2}+36 y^{2}=576\)
- \(9 x^{2}+25 y^{2}=225\)
- إجابة
-
1.
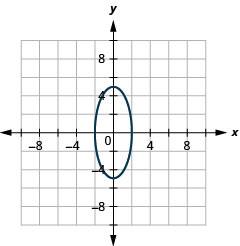
الشكل 11.3.38 3.
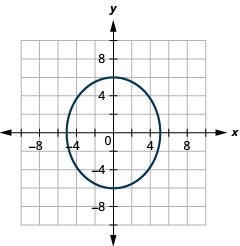
الشكل 11.3.39 5.
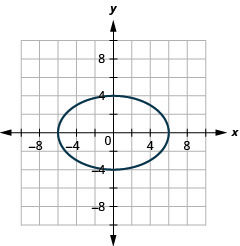
الشكل 11.3.40 7.
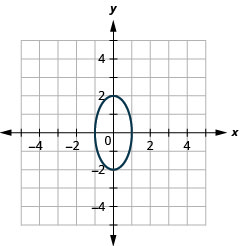
الشكل 11.3.41 9.
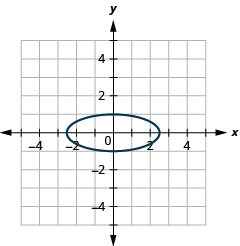
الشكل 11.3.42 11.
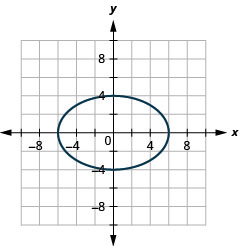
الشكل 11.3.43
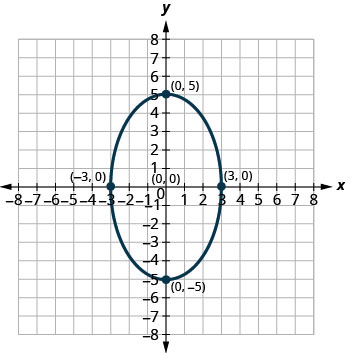
في التمارين التالية، أوجد معادلة الشكل البيضاوي الموضَّح في الرسم البياني.
1.
2.
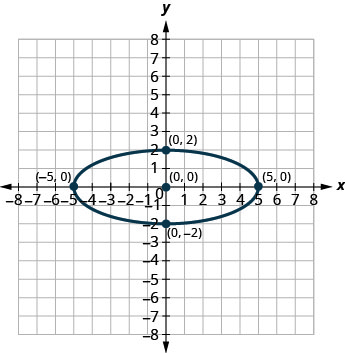
3.
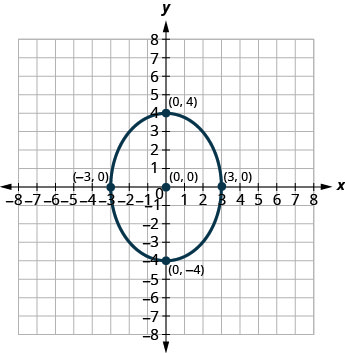
4.
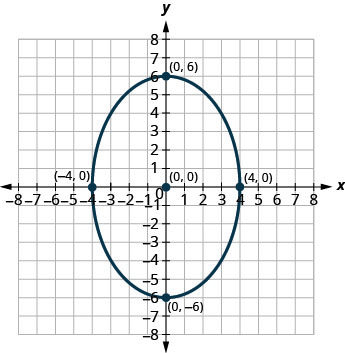
- إجابة
-
1. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
3. \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)
في التمارين التالية، قم برسم بياني لكل شكل بيضاوي.
- \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
- \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
- \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
- \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
- إجابة
-
1.
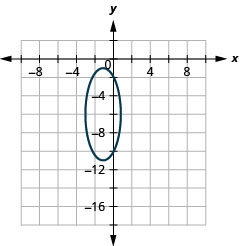
الشكل 11.3.48 3.
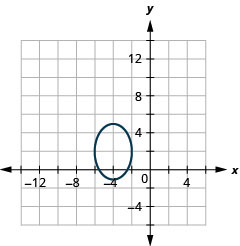
الشكل 11.3.49
في التمارين التالية، قم برسم بياني لكل معادلة بالترجمة.
- \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
- \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
- \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
- \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
- إجابة
-
1.
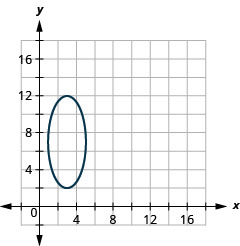
الشكل 11.3.50 3.
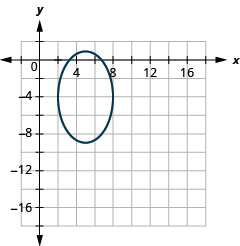
الشكل 11.3.51
في التمارين التالية،
- اكتب المعادلة في الصورة القياسية و
- رسم بياني.
- \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
- \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
- \(4 x^{2}+25 y^{2}-24 x-64=0\)
- \(9 x^{2}+4 y^{2}+56 y+160=0\)
- إجابة
-
1.
- \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
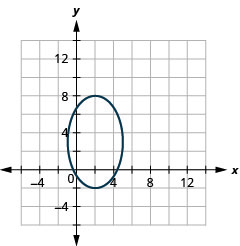
الشكل 11.3.52 3.
- \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
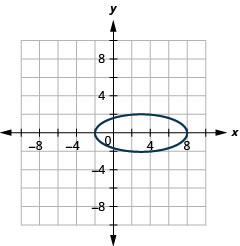
الشكل 11.3.53
في التمارين التالية، قم برسم المعادلة بيانيًا.
- \(x=-2(y-1)^{2}+2\)
- \(x^{2}+y^{2}=49\)
- \((x+5)^{2}+(y+2)^{2}=4\)
- \(y=-x^{2}+8 x-15\)
- \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
- \((x-2)^{2}+(y-3)^{2}=9\)
- \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
- \(x=4(y+1)^{2}-4\)
- \(x^{2}+y^{2}=64\)
- \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
- \(y=6 x^{2}+2 x-1\)
- \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
- إجابة
-
1.
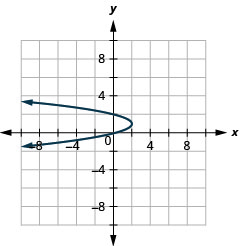
الشكل 11.3.54 3.
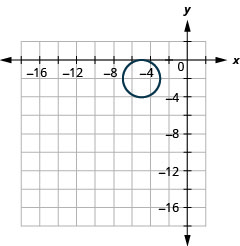
الشكل 11.3.55 5.
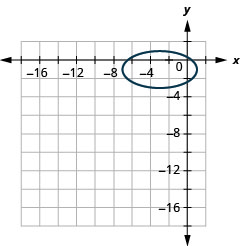
الشكل 11.3.56 7.
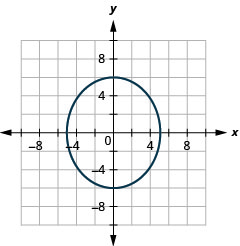
الشكل 11.3.57 9.
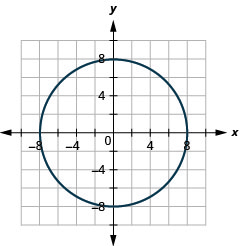
الشكل 11.3.58 11.
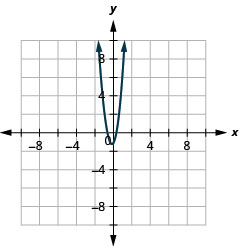
الشكل 11.3.59
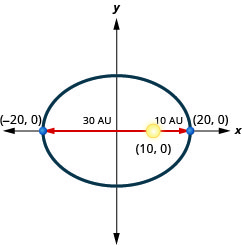
1. يتحرك كوكب في مدار بيضاوي حول الشمس. أقرب كوكب يصل إلى الشمس هو\(10\) AU تقريبًا والأبعد هو\(30\) AU تقريبًا. الشمس هي واحدة من بؤر المدار البيضاوي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار البيضاوي للكوكب.
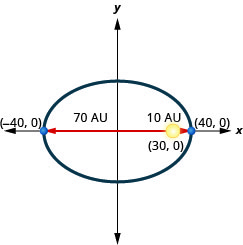
2. يتحرك كوكب في مدار بيضاوي حول الشمس. أقرب كوكب يصل إلى الشمس هو\(10\) AU تقريبًا والأبعد هو\(70\) AU تقريبًا. الشمس هي واحدة من بؤر المدار البيضاوي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار البيضاوي للكوكب.
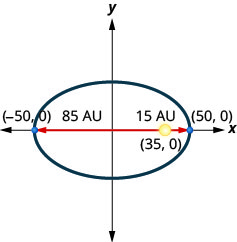
3. يتحرك مذنب في مدار بيضاوي حول الشمس. أقرب ما يصل إليه المذنب إلى الشمس هو\(15\) AU تقريبًا والأبعد هو\(85\) AU تقريبًا. الشمس هي واحدة من بؤر المدار البيضاوي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي للمذنب.
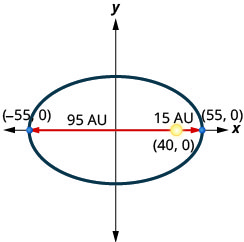
4. يتحرك مذنب في مدار بيضاوي حول الشمس. أقرب ما يصل إليه المذنب إلى الشمس هو\(15\) AU تقريبًا والأبعد هو\(95\) AU تقريبًا. الشمس هي واحدة من بؤر المدار البيضاوي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي للمذنب.
- إجابة
-
1. \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)
3. \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)
- بكلماتك الخاصة، حدد الشكل البيضاوي واكتب معادلة القطع الناقص المتمركز عند الأصل في الشكل القياسي. ارسم رسمًا تخطيطيًا للقطع الناقص الذي يصف المركز والرؤوس والمحاور الرئيسية والثانوية.
- اشرح بكلماتك الخاصة كيفية الحصول على المحاور من المعادلة في النموذج القياسي.
- قارن وقارن بين الرسوم البيانية للمعادلات\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) و\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).
- اشرح بكلماتك الخاصة الفرق بين قمة الرأس وتركيز القطع الناقص.
- إجابة
-
1. قد تختلف الإجابات
3. قد تختلف الإجابات
فحص ذاتي
أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.
ب- ماذا تخبرك قائمة التحقق هذه عن إتقانك لهذا القسم؟ ما الخطوات التي ستتخذها للتحسين؟


