11.4: الأشكال البيضاوية
- Page ID
- 201810
في نهاية هذا القسم، ستكون قادرًا على:
- رسم بياني للقطع الناقص مع المركز عند نقطة الأصل
- ابحث عن معادلة الشكل البيضاوي مع المركز عند نقطة الأصل
- ارسم بيانيًا بيضاويًا مع عدم وجود المركز في الأصل
- حل التطبيق باستخدام علامات الحذف
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- رسم بياني\(y=(x-1)^{2}-2\) باستخدام التحويلات.
إذا فاتتك هذه المشكلة، راجع مثال 9.57. - أكمل المربع:\(x^{2}-8 x=8\).
إذا فاتتك هذه المشكلة، راجع مثال 9.12. - اكتب في النموذج القياسي. \(y=2 x^{2}-12 x+14\)
إذا فاتتك هذه المشكلة، راجع المثال 9.59.
رسم بياني للقطع الناقص مع المركز عند الأصل
القسم المخروطي التالي الذي سننظر إليه هو شكل بيضاوي. نحدد الشكل البيضاوي على أنه جميع النقاط في المستوى حيث يكون مجموع المسافات من نقطتين ثابتتين ثابتًا. كل نقطة من النقاط المعطاة تسمى محور القطع الناقص.
القطع الناقص هو كل النقاط في المستوى حيث يكون مجموع المسافات من نقطتين ثابتتين ثابتًا. كل نقطة من النقاط الثابتة تسمى محور القطع الناقص.
يمكننا رسم شكل بيضاوي عن طريق أخذ طول ثابت من الخيط المرن وربط الأطراف بمسندين للإبهام. نستخدم قلمًا لسحب الخيط المشدود وتدويره حول مسندي الإبهام. الشكل الذي ينتج هو شكل بيضاوي.
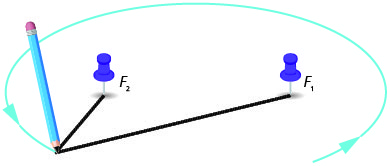
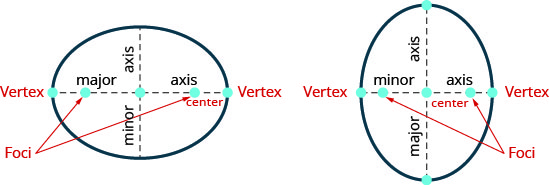
يتقاطع الخط المرسوم عبر البؤر مع الشكل البيضاوي في نقطتين. كل نقطة تسمى قمة الشكل البيضاوي. يُطلق على المقطع الذي يربط الرؤوس اسم المحور الرئيسي. يُطلق على نقطة منتصف المقطع اسم مركز القطع الناقص. يُطلق على المقطع العمودي على المحور الرئيسي الذي يمر عبر المركز ويتقاطع مع الشكل البيضاوي في نقطتين اسم المحور الصغير.
ذكرنا سابقًا أن هدفنا هو ربط هندسة المخروط بالجبر. يمنحنا وضع القطع الناقص على نظام إحداثيات مستطيل هذه الفرصة. في الشكل، وضعنا الشكل البيضاوي بحيث\(((−c,0),(c,0))\) تكون البؤر على\(x\) المحور -والمركز هو الأصل.
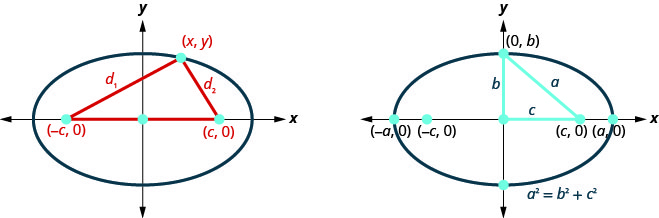
ينص التعريف على أن مجموع المسافة من البؤر إلى النقطة\((x,y)\) ثابت. \(d_{1}+d_{2}\)هذا هو الثابت الذي سنسميه\(2a\) كذلك،\(d_{1}+d_{2}=2 a\). سنستخدم صيغة المسافة لتقودنا إلى صيغة جبرية للقطع الناقص.
\(d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a\)
استخدم صيغة المسافة للبحث\(d_{1},d_{2}\).
\(\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a\)
بعد القضاء على الجذور والتبسيط، نحصل على:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1\)
لتبسيط معادلة القطع الناقص، نسمح لـ\(a^{2}−c^{2}=b^{2}\) .So، معادلة القطع الناقص المتمركز عند الأصل في الشكل القياسي هي:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
لرسم الشكل البيضاوي، سيكون من المفيد معرفة نقاط الاعتراض. سنجد\(x\) -Intercepts و\(y\) -Intercepts باستخدام الصيغة.
\(y\)- عمليات الاعتراض
دعونا\(x=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}\)
\(y\)عمليات الاعتراض - هي\((0,b)\) و\((0, -b)\).
\(x\)- عمليات الاعتراض
دعونا\(y=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
\(x\)عمليات الاعتراض - هي\((a,0)\) و\((-a,0)\).
الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((0,0)\)
الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((0,0)\)، هو
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
\(x\)عمليات الاعتراض - هي\((a,0)\) و\((−a,0)\).
\(y\)عمليات الاعتراض - هي\((0,b)\) و\((0,−b)\).
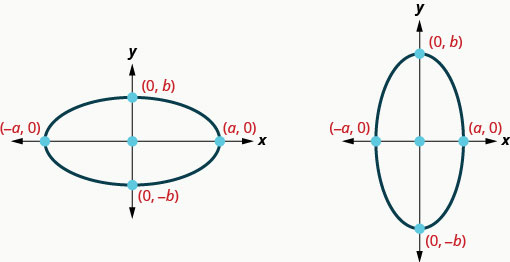
لاحظ أنه عندما يكون المحور الرئيسي أفقيًا،\(a\) ستكون قيمته أكبر من قيمة المحور الرئيسي\(b\) وعندما يكون المحور الرئيسي عموديًا،\(b\) ستكون قيمته أكبر من قيمة\(a\). سنستخدم هذه المعلومات لرسم شكل بيضاوي متمركز في الأصل.
الشكل البيضاوي مع المركز\((0,0)\)
| \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) | \(a>b\) | \(b>a\) |
|---|---|---|
| المحور الرئيسي | على\(x\) المحور -. | \(y\)على المحور |
| \(x\)- عمليات الاعتراض | \((-a, 0),(a, 0)\) | |
| \(y\)- عمليات الاعتراض | \((0,-b),(0, b)\) |
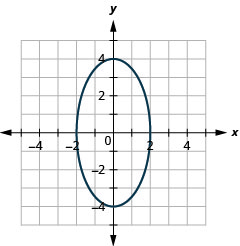
رسم بياني:\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).
الحل:
| الخطوة 1. اكتب المعادلة في الصورة القياسية. | إنه في شكل قياسي. | \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) |
| الخطوة 2. حدد ما إذا كان المحور الرئيسي أفقيًا أم رأسيًا. | نظرًا\(9\) لأنه\(9>4\) في\(y^{2}\) المصطلح، يكون المحور الرئيسي عموديًا. | المحور الرئيسي عمودي. |
| الخطوة 3. ابحث عن نقاط نهاية المحور الرئيسي. |
ستكون نقاط النهاية هي\(y\) -intercepts. منذ\(b^{2}=9\) ذلك الحين\(b=\pm 3\). نقاط النهاية للمحور الرئيسي هي\((0,3),(0,-3)\). |
نقاط النهاية للمحور الرئيسي هي\((0,3),(0,-3)\). |
| الخطوة 4. ابحث عن نقاط نهاية المحور الثانوي. | ستكون نقاط النهاية هي\(x\) -intercepts.
منذ\(a^{2}=4\) ذلك الحين\(a=\pm 2\). نقاط النهاية للمحور الرئيسي هي\((2,0),(-2,0)\). |
نقاط النهاية للمحور الرئيسي هي\((2,0),(-2,0)\). |
| الخطوة 5. ارسم الشكل البيضاوي. | .png) |
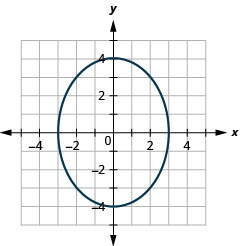
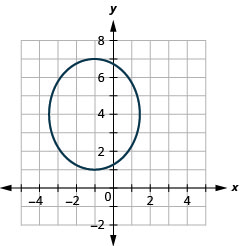
رسم بياني:\(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\).
- إجابة
-
الشكل 11.3.7
رسم بياني:\(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\).
- إجابة
-
الشكل 11.3.8
نحن نلخص الخطوات كمرجع.
كيفية رسم شكل بيضاوي مع المركز\((0,0)\).
- اكتب المعادلة في الصورة القياسية.
- حدد ما إذا كان المحور الرئيسي أفقيًا أم رأسيًا.
- ابحث عن نقاط نهاية المحور الرئيسي.
- ابحث عن نقاط نهاية المحور الصغير
- ارسم الشكل البيضاوي.
في بعض الأحيان، يجب وضع المعادلة أولاً في شكل قياسي.
رسم بياني\(x^{2}+4 y^{2}=16\).
الحل:
| نحن ندرك هذا على أنه معادلة القطع الناقص نظرًا لأن كلا\(x\)\(y\) المصطلحين مربعان ولهما معاملات مختلفة. |
\(x^{2}+4 y^{2}=16\) |
| للحصول على المعادلة في الصورة القياسية، قسّم كلا الطرفين\(16\) بحيث تكون المعادلة مساوية لـ\(1\). |
\(\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}\) |
| قم بالتبسيط. | \(\frac{x^{2}}{16}+\frac{y^{2}}{4}=1\) |
| المعادلة في الشكل القياسي. يتركز الشكل البيضاوي في الأصل. |
المركز هو\((0,0)\). |
| نظرًا\(16\) لأنه\(16>4\) في\(x^{2}\) المصطلح، يكون المحور الرئيسي أفقيًا. |
|
| \(a^{2}=16, a=\pm 4\) \(b^{2}=4, \quad b=\pm 2\) |
الرؤوس هي\((4,0),(−4,0)\). نقاط النهاية للمحور الثانوي هي \((0,2),(0,−2)\). |
| ارسم القطع المكافئ. | 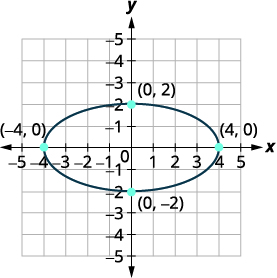 |
رسم بياني\(9 x^{2}+16 y^{2}=144\).
- إجابة
-
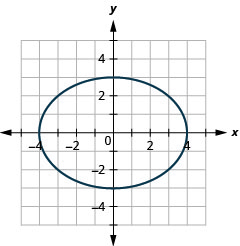
الشكل 11.3.10
رسم بياني\(16 x^{2}+25 y^{2}=400\).
- إجابة
-
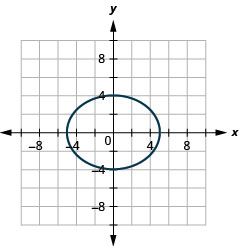
الشكل 11.3.11
ابحث عن معادلة القطع الناقص مع المركز عند نقطة الأصل
إذا أُعطينا الرسم البياني للقطع الناقص، يمكننا إيجاد معادلة القطع الناقص.
أوجد معادلة الشكل البيضاوي الموضَّح.
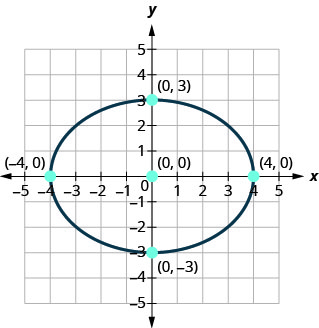
الحل:
نحن ندرك هذا على أنه شكل بيضاوي يتركز في الأصل.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
نظرًا لأن المحور الرئيسي أفقي والمسافة من المركز إلى الرأس هي\(4\)، فنحن نعرف\(a=4\) ذلك\(a^{2}=16\).
\(\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1\)
المحور الصغير عمودي والمسافة من المركز إلى الشكل البيضاوي هي\(3\) كما نعلم\(b=3\) وهكذا\(b^{2}=9\).
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
أوجد معادلة الشكل البيضاوي الموضَّح.
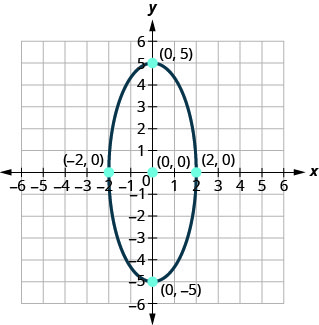
- إجابة
-
\(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
أوجد معادلة الشكل البيضاوي الموضَّح.
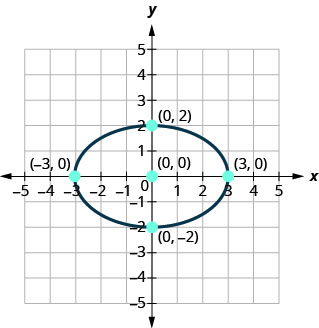
- إجابة
-
\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)
رسم بياني لشكل بيضاوي مع عدم وجود المركز في الأصل
لقد تمحورت جميع علامات الحذف التي نظرنا إليها حتى الآن في الأصل. سننظر الآن في الأشكال البيضاوية التي يقع مركزها\((h,k)\).
المعادلة هي\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) وعندما يكون المحور الرئيسي أفقيًا\(a>b\)، وبالتالي تكون المسافة من المركز إلى الرأس\(a\). عندما يكون\(b>a\) المحور الرئيسي عموديًا، تكون المسافة من المركز إلى قمة الرأس\(b\).
الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((h,k)\)
الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((h,k)\)، هو
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
عندما يكون\(a>b\) المحور الرئيسي أفقيًا، تكون المسافة من المركز إلى قمة الرأس\(a\).
عندما يكون\(b>a\) المحور الرئيسي عموديًا، تكون المسافة من المركز إلى قمة الرأس\(b\).
رسم بياني:\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\).
الحل:
| المعادلة في الشكل القياسي،\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). | \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) |
| يتركز الشكل البيضاوي في\((h,k)\). | المركز هو\((3,1)\). |
| نظرًا\(9\) لأنه\(9>4\) في\(x^{2}\) المصطلح، يكون المحور الرئيسي أفقيًا. | |
| \(a^{2}=9, a=\pm 3\) \(b^{2}=4, b=\pm 2\) |
المسافة من المركز إلى الرؤوس هي\(3\). المسافة من المركز إلى نقاط النهاية للمحور الصغير هي\(2\). |
| ارسم الشكل البيضاوي. | 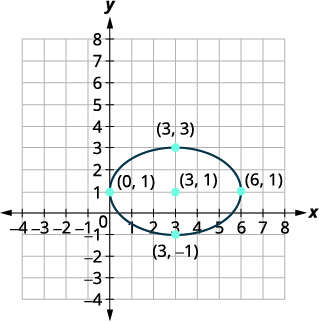 |
رسم بياني:\(\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1\).
- إجابة
-
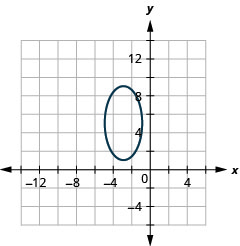
الشكل 11.3.16
رسم بياني:\(\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1\).
- إجابة
-
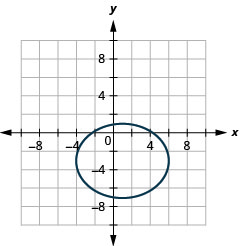
الشكل 11.3.17
إذا نظرنا إلى معادلات\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) و\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\)، نرى أن كلاهما عبارة عن حذف مع\(a=3\) و\(b=2\). لذلك سيكون لديهم نفس الحجم والشكل. إنهم مختلفون من حيث أنهم لا يملكون نفس المركز.
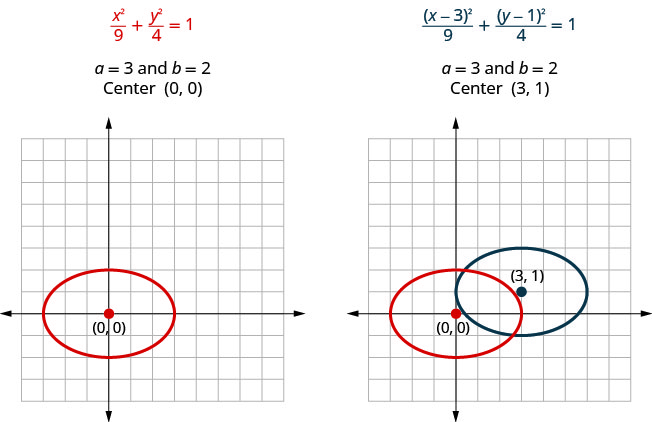
لاحظ في الرسم البياني أعلاه أنه كان بإمكاننا رسم بياني\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) بالترجمات. قمنا بنقل القطع الناقص الأصلي إلى\(3\) الوحدات الصحيحة ثم إلى أعلى\(1\) الوحدة.
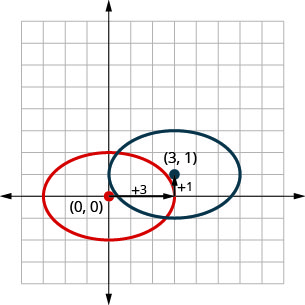
في المثال التالي، سنستخدم طريقة الترجمة لرسم القطع الناقص.
رسم بياني\(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) بالترجمة.
الحل:
سيكون لهذا الشكل البيضاوي نفس الحجم والشكل مثل\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) مركزه\((0,0)\). نرسم هذا الشكل البيضاوي أولاً.
| المركز هو\((0,0)\). | المركز\((0,0)\) |
| نظرًا لأن\(16>9\) المحور الرئيسي أفقي. | |
| \(a^{2}=16, a=\pm 4\) \(b^{2}=9, \quad b=\pm 3\) |
الرؤوس هي\((4,0),(−4,0)\). نقاط النهاية للمحور الثانوي هي \((0,3),(0,−3)\). |
| ارسم الشكل البيضاوي. | 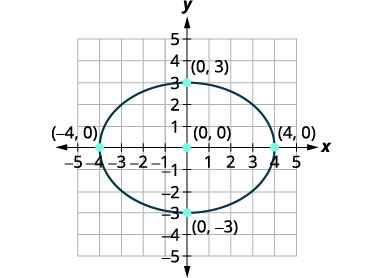 |
| المعادلة الأصلية في شكل قياسي،\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). | \(\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) |
| يتركز الشكل البيضاوي في\((h,k)\). | المركز هو\((-4,6)\). |
| نترجم الرسم البياني\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) لأربع وحدات إلى اليسار ثم\(6\) الوحدات العلوية. تحقق من أن المركز موجود\((−4,6)\). الشكل البيضاوي الجديد هو الشكل البيضاوي الذي تكون معادلته \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\). |
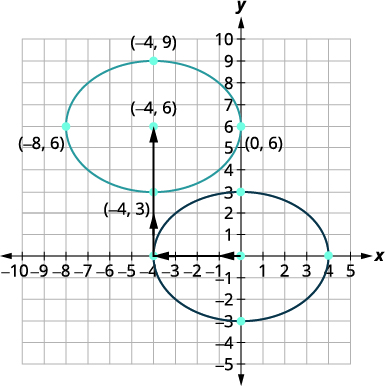 |
رسم بياني\(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1\) بالترجمة.
- إجابة
-
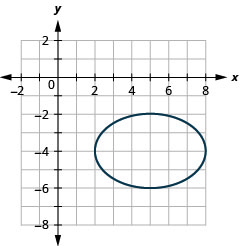
الشكل 11.3.22
رسم بياني\(\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1\) بالترجمة.
- إجابة
-
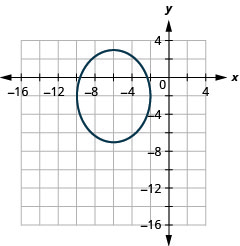
الشكل 11.3.23
عندما تحتوي المعادلة على كل من a\(x^{2}\) و a\(y^{2}\) بمعاملات مختلفة، فإننا نتحقق من أنها علامة حذف بوضعها في الشكل القياسي. سنتمكن بعد ذلك من رسم المعادلة بيانيًا.
اكتب المعادلة\(x^{2}+4 y^{2}-4 x+24 y+24=0\) في الصورة القياسية والرسم البياني.
الحل:
نضع المعادلة في الشكل القياسي بإكمال المربعات في كل من\(x\) و\(y\).
| \(x^{2}+4 y^{2}-4 x+24 y+24=0\) | |
| أعد كتابة تجميع\(x\) المصطلحات\(y\) والمصطلحات. | 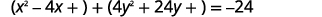 |
| اجعل المعامِلات\(y^{2}\) تساوي\(x^{2}\) وتساوي\(1\). | 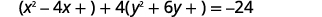 |
| أكمل المربعات. | 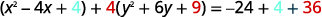 |
| اكتب كمربعات ذات حدين. | 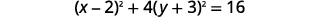 |
| قسّم كلا\(1\) الجانبين\(16\) للوصول إلى اليمين. | 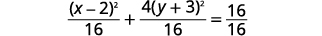 |
| قم بالتبسيط. | 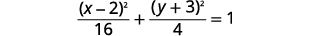 |
| المعادلة في الشكل القياسي،\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) | 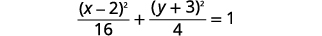 |
| يتركز الشكل البيضاوي في\((h,k)\). | المركز هو\((2,-3)\). |
|
نظرًا\(16\) لأنه\(16>4\) في\(x^{2}\) المصطلح، يكون المحور الرئيسي أفقيًا. \(a^{2}=16, a=\pm 4\) |
المسافة من المركز إلى الرؤوس هي\(4\). المسافة من المركز إلى نقاط النهاية للمحور الصغير هي\(2\). |
| ارسم الشكل البيضاوي. | 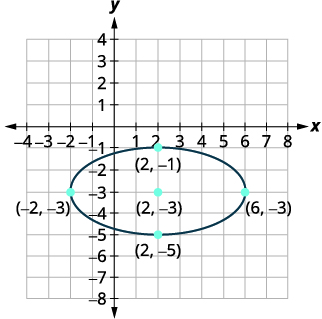 |
- اكتب المعادلة\(6 x^{2}+4 y^{2}+12 x-32 y+34=0\) في الصورة القياسية و
- رسم بياني.
- إجابة
-
- \(\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1\)
الشكل 11.3.32
- اكتب المعادلة\(4 x^{2}+y^{2}-16 x-6 y+9=0\) في الصورة القياسية و
- رسم بياني.
- إجابة
-
- \(\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1\)
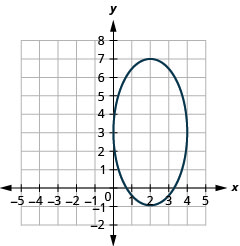
الشكل 11.3.33
حل التطبيق باستخدام علامات الحذف
تتبع مدارات الكواكب حول الشمس مسارات بيضاوية.
يتحرك بلوتو (كوكب قزم) في مدار بيضاوي حول الشمس. أقرب كوكب بلوتو إلى الشمس هو وحدات\(30\) فلكية تقريبًا (AU) وأبعدها هو\(50\) AU تقريبًا. الشمس هي واحدة من بؤر المدار الإهليلجي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي لبلوتو.
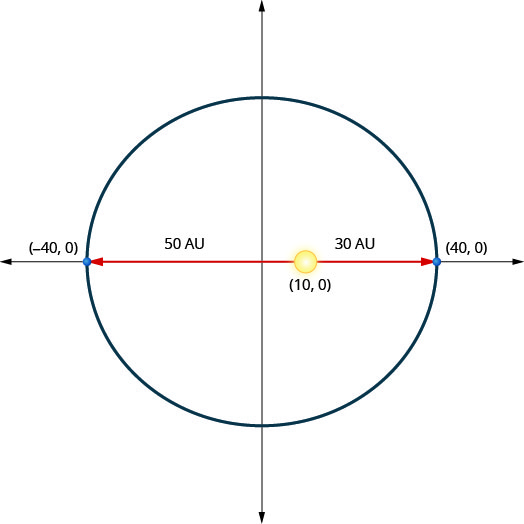
الحل:
نحن ندرك هذا على أنه شكل بيضاوي يتركز في الأصل.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
نظرًا لأن المحور الرئيسي أفقي والمسافة من المركز إلى الرأس هي\(40\)، فنحن نعرف\(a=40\) ذلك\(a^{2}=1600\).
\(\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1\)
المحور الصغير عمودي ولكن نقاط النهاية غير مذكورة. للعثور على ذلك،\(b\) سنستخدم موقع الشمس. نظرًا لأن الشمس هي محور القطع الناقص عند هذه النقطة\((10,0)\)، فإننا نعلم ذلك\(c=10\). استخدم هذا لحلها\(b^{2}\).
\(b^{2}=a^{2}-c^{2}\)
\(b^{2}=40^{2}-10^{2}\)
\(b^{2}=1600-100\)
\(b^{2}=1500\)
استبدل\(a^{2}\)\(b^{2}\) وفي الشكل القياسي للقطع الناقص.
\(\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1\)
يتحرك كوكب في مدار بيضاوي حول الشمس. أقرب كوكب يصل إلى الشمس هو\(20\) AU تقريبًا والأبعد هو\(30\) AU تقريبًا. الشمس هي واحدة من بؤر المدار الإهليلجي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي للكوكب.
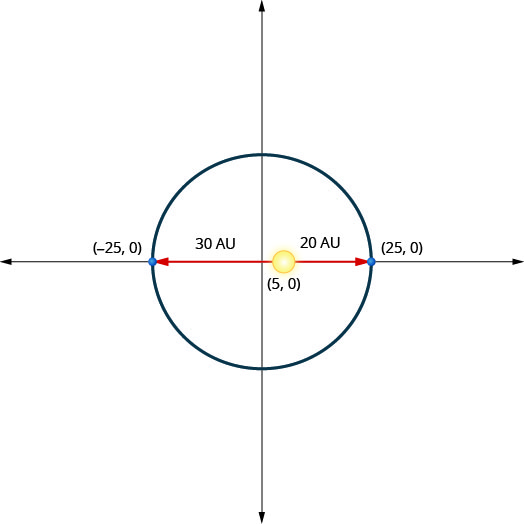
- إجابة
-
\(\frac{x^{2}}{625}+\frac{y^{2}}{600}=1\)
يتحرك كوكب في مدار بيضاوي حول الشمس. أقرب كوكب يصل إلى الشمس هو\(20\) AU تقريبًا والأبعد هو\(50\) AU تقريبًا. الشمس هي واحدة من بؤر المدار الإهليلجي. عند ترك الشكل البيضاوي في نقطة الأصل ووضع علامات على المحاور في AU، سيبدو المدار كما هو موضح أدناه. استخدم الرسم البياني لكتابة معادلة للمدار الإهليلجي للكوكب.
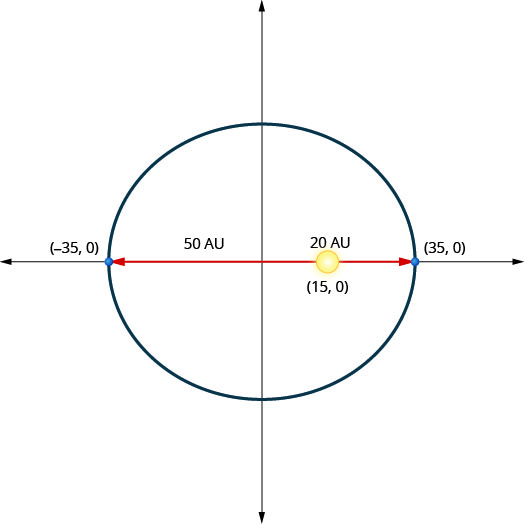
- إجابة
-
\(\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على إرشادات إضافية وممارسة باستخدام علامات الحذف.
- المقاطع المخروطية: رسم الأشكال البيضاوية - الجزء 1
- المقاطع المخروطية: رسم الأشكال البيضاوية - الجزء 2
- معادلة القطع الناقص من الرسم البياني
المفاهيم الرئيسية
- الشكل البيضاوي: القطع الناقص هو كل النقاط في المستوى حيث يكون مجموع المسافات من نقطتين ثابتتين ثابتًا. كل نقطة من النقاط الثابتة تسمى محور القطع الناقص.
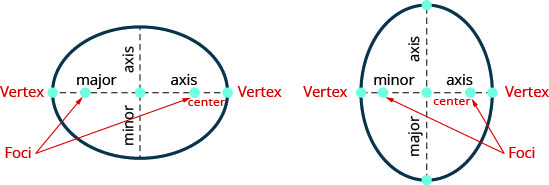
الشكل 11.3.37
- إذا رسمنا خطًا عبر البؤر، يتقاطع الشكل البيضاوي في نقطتين - يُطلق على كل منهما رأس الشكل البيضاوي.
يُطلق على المقطع الذي يربط الرؤوس اسم المحور الرئيسي.
يُطلق على نقطة منتصف المقطع اسم مركز القطع الناقص.
يُطلق على المقطع العمودي على المحور الرئيسي الذي يمر عبر المركز ويتقاطع مع الشكل البيضاوي في نقطتين اسم المحور الصغير. - الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((0,0)\): الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((0,0)\)، هو
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
\(x\)عمليات الاعتراض - هي\((a,0)\) و\((−a,0)\).
\(y\)عمليات الاعتراض - هي\((0,b)\) و\((0,−b)\). - كيفية عمل القطع الناقص مع المركز\((0,0)\)
- اكتب المعادلة في الصورة القياسية.
- حدد ما إذا كان المحور الرئيسي أفقيًا أم رأسيًا.
- ابحث عن نقاط نهاية المحور الرئيسي.
- ابحث عن نقاط نهاية المحور الصغير
- ارسم الشكل البيضاوي.
- الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((h,k)\): الشكل القياسي لمعادلة الشكل البيضاوي مع المركز\((h,k)\)، هو
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
عندما يكون\(a>b\) المحور الرئيسي أفقيًا، تكون المسافة من المركز إلى قمة الرأس\(a\).
عندما يكون\(b>a\) المحور الرئيسي عموديًا، تكون المسافة من المركز إلى قمة الرأس\(b\).
مسرد المصطلحات
- الشكل البيضاوي
- القطع الناقص هو كل النقاط في المستوى حيث يكون مجموع المسافات من نقطتين ثابتتين ثابتًا.


