11.3E: تمارين
- Page ID
- 201781
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
الممارسة تجعل من الكمال
في التمارين التالية، قم برسم بياني لكل معادلة باستخدام الخصائص.
- \(y=-x^{2}+4 x-3\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
- \(y=8 x^{2}-10 x+3\)
- إجابة
-
1.
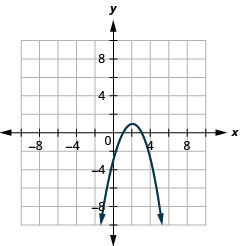
الشكل 11.2.83 3.
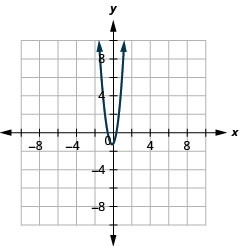
الشكل 11.2.84
في التمارين التالية،
- اكتب المعادلة في الصورة القياسية و
- استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
- \(y=-x^{2}+2 x-4\)
- \(y=2 x^{2}+4 x+6\)
- \(y=-2 x^{2}-4 x-5\)
- \(y=3 x^{2}-12 x+7\)
- إجابة
-
1.
- \(y=-(x-1)^{2}-3\)
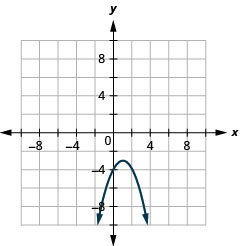
الشكل 11.2.85 3.
- \(y=-2(x+1)^{2}-3\)
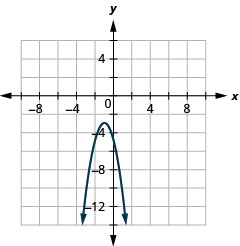
الشكل 11.2.86
في التمارين التالية، قم برسم بياني لكل معادلة باستخدام الخصائص.
- \(x=-2 y^{2}\)
- \(x=3 y^{2}\)
- \(x=4 y^{2}\)
- \(x=-4 y^{2}\)
- \(x=-y^{2}-2 y+3\)
- \(x=-y^{2}-4 y+5\)
- \(x=y^{2}+6 y+8\)
- \(x=y^{2}-4 y-12\)
- \(x=(y-2)^{2}+3\)
- \(x=(y-1)^{2}+4\)
- \(x=-(y-1)^{2}+2\)
- \(x=-(y-4)^{2}+3\)
- \(x=(y+2)^{2}+1\)
- \(x=(y+1)^{2}+2\)
- \(x=-(y+3)^{2}+2\)
- \(x=-(y+4)^{2}+3\)
- \(x=-3(y-2)^{2}+3\)
- \(x=-2(y-1)^{2}+2\)
- \(x=4(y+1)^{2}-4\)
- \(x=2(y+4)^{2}-2\)
- إجابة
-
1.
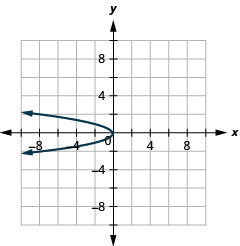
الشكل 11.2.87 3.
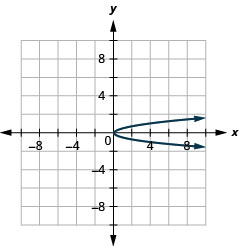
الشكل 11.2.88 5.
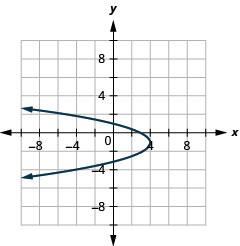
الشكل 11.2.89 7.
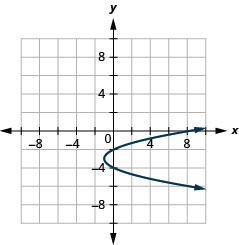
الشكل 11.2.90 9.
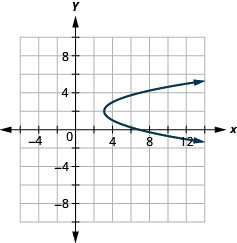
الشكل 11.2.91 11.
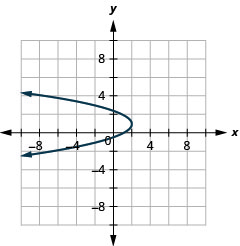
الشكل 11.2.92 13.
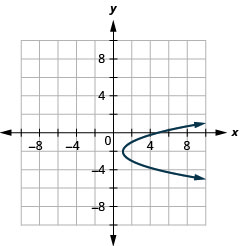
الشكل 11.2.93 15.
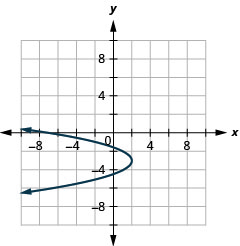
الشكل 11.2.94 17.
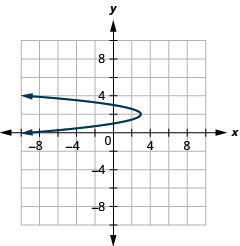
الشكل 11.2.95 19.
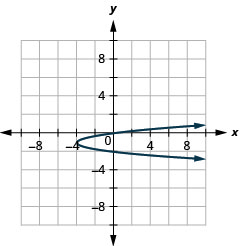
الشكل 11.2.96
في التمارين التالية،
- اكتب المعادلة في الصورة القياسية و
- استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
- \(x=y^{2}+4 y-5\)
- \(x=y^{2}+2 y-3\)
- \(x=-2 y^{2}-12 y-16\)
- \(x=-3 y^{2}-6 y-5\)
- إجابة
-
1.
- \(x=(y+2)^{2}-9\)
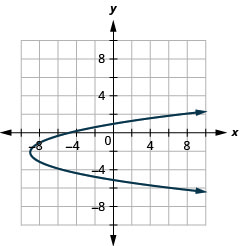
الشكل 11.2.97 3.
- \(x=-2(y+3)^{2}+2\)
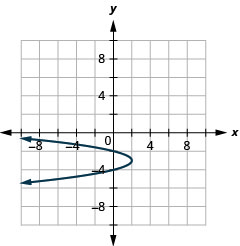
الشكل 11.2.98
في التمارين التالية، قم بمطابقة كل رسم بياني بإحدى المعادلات التالية:
- \(x^{2}+y^{2}=64\)
- \(x^{2}+y^{2}=49\)
- \((x+5)^{2}+(y+2)^{2}=4\)
- \((x-2)^{2}+(y-3)^{2}=9\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
1.
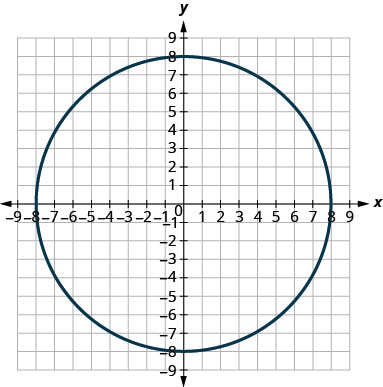
2.
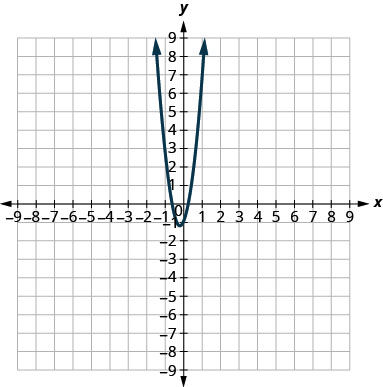
3.
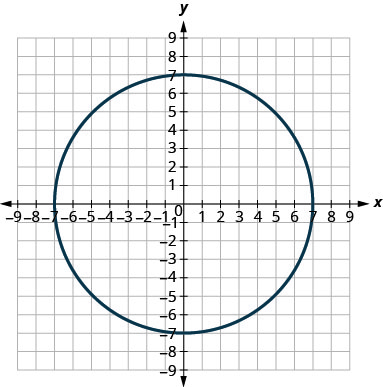
4.
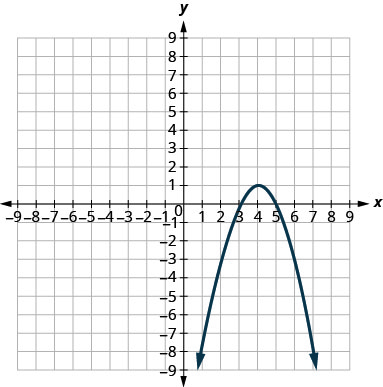
5.
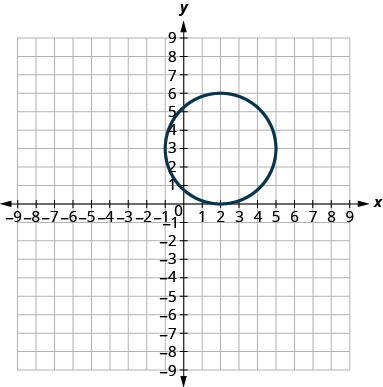
6.
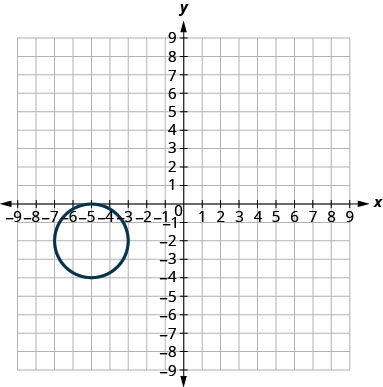
- إجابة
-
1. أ
3. ب
5. د
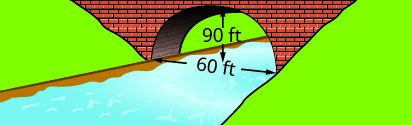
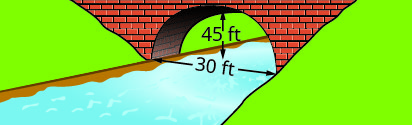
اكتب المعادلة في الصورة القياسية للقوس المكافئ المتكوَّن في أساس الجسر الموضَّح. استخدم الجانب الأيسر السفلي من الجسر كنقطة أصل\((0, 0)\).
1.
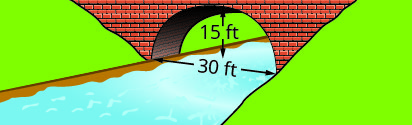
2.
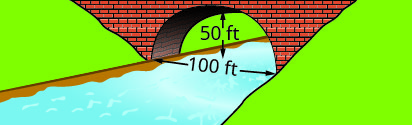
3.
4.
- إجابة
-
1. \(y=-\frac{1}{15}(x-15)^{2}+15\)
3. \(y=-\frac{1}{10}(x-30)^{2}+90\)
- بكلماتك الخاصة، حدد المكافئ.
- هل المكافئ\(y=x^{2}\) دالة؟ هل المكافئ\(x=y^{2}\) دالة؟ اشرح لماذا أو لماذا لا.
- اكتب معادلة القطع المكافئ الذي يفتح لأعلى أو لأسفل في الصورة القياسية ومعادلة القطع المكافئ الذي يفتح يسارًا أو يمينًا في الصورة القياسية. قدم رسمًا بيانيًا للأجزاء المكافئة لكل منها، وقم بتسمية قمة الرأس ومحور التماثل.
- اشرح بكلماتك الخاصة كيف يمكنك معرفة ما إذا كان القطع المكافئ يفتح لأعلى أو لأسفل أو يسارًا أو يمينًا من المعادلة.
- إجابة
-
1. قد تختلف الإجابات
3. قد تختلف الإجابات
فحص ذاتي
أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.
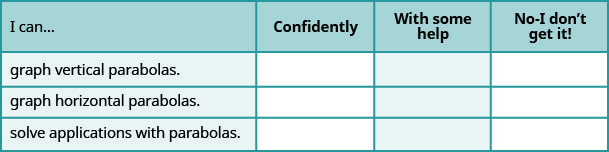
ب- بعد مراجعة قائمة التحقق هذه، ماذا ستفعل لتصبح واثقًا من جميع الأهداف؟