11.3: بارابولاس
- Page ID
- 201770
في نهاية هذا القسم، ستكون قادرًا على:
- الأشكال الرأسية للرسم البياني
- الأشكال الجانبية الأفقية للرسم البياني
- حل التطبيقات باستخدام بارابولاس
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- رسم بياني:\(y=-3 x^{2}+12 x-12\).
إذا فاتتك هذه المشكلة، راجع مثال 9.47. - حل بإكمال المربع:\(x^{2}-6 x+6=0\).
إذا فاتتك هذه المشكلة، راجع مثال 9.12. - اكتب في النموذج القياسي:\(y=3 x^{2}-6 x+5\).
إذا فاتتك هذه المشكلة، راجع المثال 9.59.
الرسم البياني: البارابولاس الرأسية
القسم المخروطي التالي الذي سننظر إليه هو القطع المكافئ. نحدد المكافئ على أنه جميع النقاط في المستوى التي هي نفس المسافة من نقطة ثابتة وخط ثابت. تسمى النقطة الثابتة بالتركيز، والخط الثابت يسمى دليل المكافئ.
المكافئ هو كل النقاط في المستوى الذي يقع على نفس المسافة من نقطة ثابتة وخط ثابت. تسمى النقطة الثابتة بالتركيز، والخط الثابت يسمى دليل المكافئ.
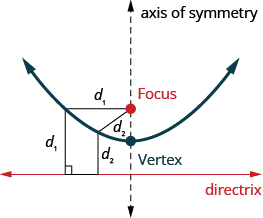
في السابق، تعلمنا رسم البارابولاس الرأسية من النموذج العام أو النموذج القياسي باستخدام الخصائص. ستعمل هذه الأساليب هنا أيضًا. سنلخص الخصائص هنا.
بارابولاس عمودية
|
نموذج عام \(y=a x^{2}+b x+c\) |
نموذج قياسي \(y=a(x-h)^{2}+k\) |
|
|---|---|---|
| اتجاه | \ (y=a x^ {2} +b x+c\) ">\(a>0\) لأعلى؛\(a<0\) لأسفل | \ (y=a (x-h) ^ {2} +k\) ">\(a>0\) لأعلى؛\(a<0\) لأسفل |
| محور التماثل | \ (y=a x^ {2} +ب x+c\) ">\(x=-\dfrac{b}{2 a}\) | \ (y=a (x-h) ^ {2} +k\) ">\(x=h\) |
| فيرتكس | \ (y=a x^ {2} +b x+c\) ">بديل\(x=-\dfrac{b}{2 a}\) وحل لـ\(y .\) |
\ (y=a (x-h) ^ {2} +k\) ">\((h, k)\) |
| \(y\)-اعتراض | \ (y=a x^ {2} +ب x+c\) ">Let\(x=0\) | \ (y=a (x-h) ^ {2} +k\) ">دع\(x=0\) |
| \(x\)- عمليات الاعتراض | \ (y=a x^ {2} +ب x+c\) ">Let\(y=0\) | \ (y=a (x-h) ^ {2} +k\) ">دع\(y=0\) |
تُظهر الرسوم البيانية كيف تبدو المظلات عندما تفتح لأعلى أو لأسفل. إن موقفهم فيما يتعلق\(y\) بالمحور\(x\) - أو - هو مجرد مثال.
لرسم مكافئ من هذه النماذج، استخدمنا الخطوات التالية.
كيفية رسم بارابولاس عمودية\(y=a x^{2}+b x+c\) أو\(f(x)=a(x-h)^{2}+k\) استخدام الخصائص.
- الخطوة 1: حدد ما إذا كان القطع المكافئ يفتح لأعلى أو لأسفل.
- الخطوة 2. أوجد محور التماثل.
- الخطوة 3. ابحث عن قمة الرأس.
- الخطوة 4. ابحث\(y\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(y\) المقطوع عبر محور التماثل.
- الخطوة 5. ابحث عن\(x\) -Intercepts.
- الخطوة 6. رسم بياني للقطع المكافئ.
يستعرض المثال التالي طريقة رسم المكافئ بيانيًا من الشكل العام لمعادلته.
رسم بياني\(y=-x^{2}+6 x-8\) باستخدام الخصائص.
الحل:
| \( \begin{align*} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt] \color{black}{y} &=-x^{2}+6 x-8 \end{align*}\) | |
| منذ\(a\) ذلك الحين\(-1\)، ينفتح المكافئ لأسفل. | |
 |
|
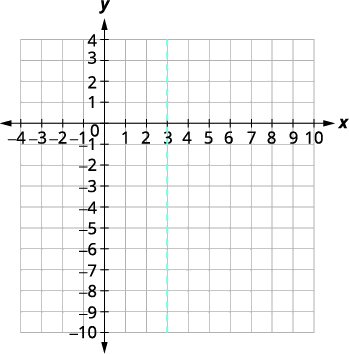
| للعثور على محور التماثل، ابحث\(x=-\dfrac{b}{2 a}\). | \( \begin{align*} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align*}\) |
| محور التماثل هو\(x=3\). | |
 |
|
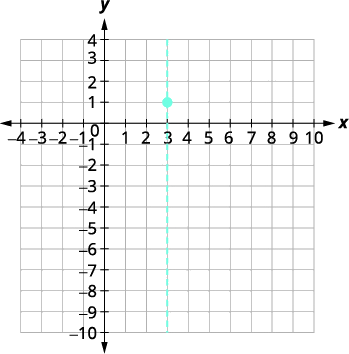
| قمة الرأس على الخط\(x=3\). | \(y=-x^{2}+6 x-8\) |
| دعونا\(x=3\). | 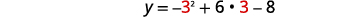 |
| \(\begin{align*} y &=-9+18-8 \\[4pt] y &=1 \end{align*}\) | |
| قمة الرأس هي\((3,1)\). | |
 |
|
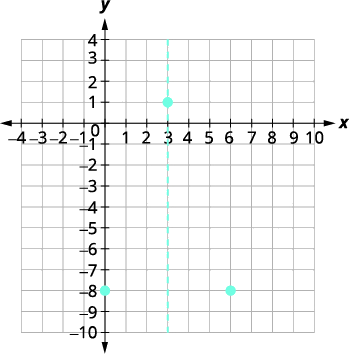
| يحدث\(y\) التقاطع عند حدوث ذلك\(x=0\). | \(y=-x^{2}+6 x-8\) |
| بديل\(x=0\). | \(y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8\) |
| قم بالتبسيط. | \(y=-8\) |
| \(y\)التقاطع هو\((0,-8)\). | |
| النقطة\((0,−8)\) هي ثلاث وحدات على يسار خط التماثل. النقطة الثلاث وحدات على يمين خط التماثل هي\((6,−8)\). | النقطة المتماثلة في\(y\) التقاطع السيني هي\((6,−8)\). |
 |
|
| يحدث\(x\) التقاطع عند حدوث ذلك\(y=0\). | \(y=-x^{2}+6 x-8\) |
| دعونا\(y=0\). | \(\color{red}{0} \color{black}{=}-x^{2}+6 x-8\) |
| عامل عامل GCF. | \(0=-\left(x^{2}-6 x+8\right)\) |
| عامل ثلاثي الحدود. | \(0=-(x-4)(x-2)\) |
| حل لـ\(x\). | \(x=4, \quad x=2\) |
| \(x\)عمليات الاعتراض الإلكترونية هي\((4,0),(2,0)\). | |
| رسم بياني للقطع المكافئ. | 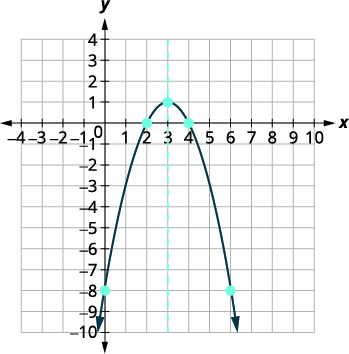 |
رسم بياني\(y=-x^{2}+5 x-6\) باستخدام الخصائص.
- إجابة
-
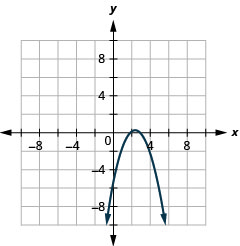
الشكل 11.2.24
رسم بياني\(y=-x^{2}+8 x-12\) باستخدام الخصائص.
- إجابة
-
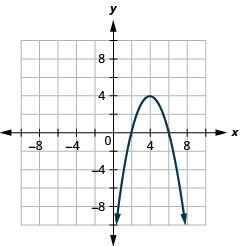
الشكل 11.2.25
يستعرض المثال التالي طريقة رسم المكافئ بيانيًا من الشكل القياسي لمعادلته,\(y=a(x-h)^{2}+k\).
اكتب\(y=3 x^{2}-6 x+5\) في النموذج القياسي ثم استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
الحل:
| أعد كتابة الدالة في\(y=a(x-h)^{2}+k\) الشكل بإكمال المربع. | \(\begin{align*} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3 \\[4pt] y &=3(x-1)^{2}+2 \end{align*}\) |
| حدد الثوابت\(a, h, k\). | \(a=3, h=1, k=2\) |
| منذ ذلك الحين\(a=2\)، ينفتح المكافئ لأعلى. | |
 |
|
| محور التماثل هو\(x=h\). | محور التماثل هو\(x=1\). |
| قمة الرأس هي\((h,k)\). | قمة الرأس هي\((1,2)\). |
| ابحث عن\(y\) التقاطع السيني عن طريق الاستبدال\(x=0\)، | \( \begin{align*} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align*} \) |
| \(y\)-اعتراض\((0,5)\) | |
| ابحث عن النقطة المتماثلة\((0,5)\) لعبور محور التماثل. | \((2,5)\) |
| ابحث عن\(x\) -Intercepts. | \(\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}\) |
| يخبرنا الجذر التربيعي لرقم سالب أن الحلول هي أرقام معقدة. لذلك لا\(x\) توجد اعتراضات. | |
| رسم بياني للقطع المكافئ. | 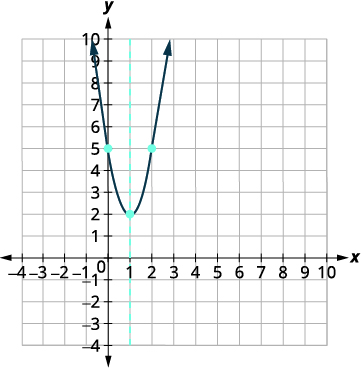 |
- اكتب\(y=2 x^{2}+4 x+5\) في النموذج القياسي و
- استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
- إجابة
-
- \(y=2(x+1)^{2}+3\)
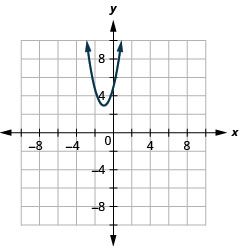
الشكل 11.2.28
- اكتب\(y=-2 x^{2}+8 x-7\) في النموذج القياسي و
- استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
- إجابة
-
- \(y=-2(x-2)^{2}+1\)
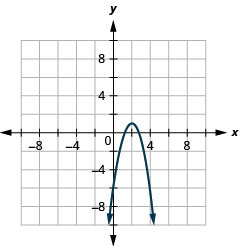
الشكل 11.2.29
رسم بياني: بارابولاس أفقية
لم يتعامل عملنا حتى الآن إلا مع الأشكال المظللة التي تنفتح لأعلى أو لأسفل. سننظر الآن في الأشكال الأفقية. تفتح هذه الأشكال المظللة إما إلى اليسار أو إلى اليمين. إذا تبادلنا الحرف «\(x\)و»\(y\) في معادلاتنا السابقة للبارابولاس، نحصل على معادلات البارابولاس التي تنفتح على اليسار أو إلى اليمين.
بارابولاس أفقية
|
نموذج عام \(x=a y^{2}+b y+c\) |
نموذج قياسي \(x=a(y-k)^{2}+h\) |
|
|---|---|---|
| اتجاه | \ (x=a y^ {2} +b y+c\) ">\(a>0\) اليمين؛\(a<0\) اليسار | \ (x=a (y-k) ^ {2} +h\) ">\(a>0\) اليمين؛\(a<0\) اليسار |
| محور التماثل | \ (x=a y^ {2} +b y+c\) ">\(y=-\dfrac{b}{2 a}\) | \ (x=a (y-k) ^ {2} +h\) ">\(y=k\) |
| فيرتكس | \ (x=a y^ {2} +b y+c\) ">بديل\(y=-\dfrac{b}{2 a}\) وحل لـ\(x .\) |
\ (x=a (y-k) ^ {2} +h\) ">\((h, k)\) |
| \(x\)- عمليات الاعتراض | \ (x=a y^ {2} +b y+c\) ">Let\(x=0\) | \ (x=a (y-k) ^ {2} +h\) ">Let\(x=0\) |
| \(y\)-اعتراض | \ (x=a y^ {2} +b y+c\) ">Let\(y=0\) | \ (x=a (y-k) ^ {2} +h\) ">Let\(y=0\) |
تُظهر الرسوم البيانية كيف تبدو البارابولاس عندما تكون على اليسار أو إلى اليمين. إن موقفهم فيما يتعلق\(y\) بالمحور\(x\) - أو - هو مجرد مثال.
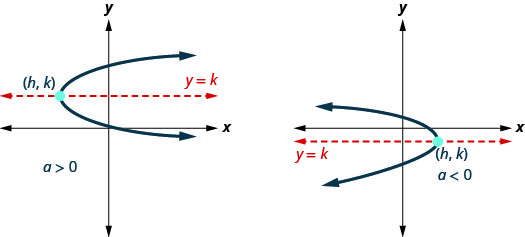
بالنظر إلى هذه الأشكال المماثلة، هل تمثل رسوماتها البيانية دالة؟ نظرًا لأن كلا الرسمين البيانيين سيفشلان في اختبار الخط العمودي، فإنهما لا يمثلان دالة.
إن رسم القطع المكافئ الذي يفتح إلى اليسار أو اليمين هو في الأساس نفس ما فعلناه للبارابولاس التي تنفتح لأعلى أو لأسفل، مع عكس\(y\) المتغيرات.\(x\)
- الخطوة 1: حدد ما إذا كان القطع المكافئ يفتح على اليسار أو إلى اليمين.
- الخطوة 2: ابحث عن محور التماثل.
- الخطوة 3: ابحث عن قمة الرأس.
- الخطوة 4: ابحث\(x\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(x\) المقطوع عبر محور التماثل.
- الخطوة 5: ابحث عن\(y\) -Intercepts.
- الخطوة 6: رسم القطع المكافئ.
رسم بياني\(x=2 y^{2}\) باستخدام الخصائص.
الحل:
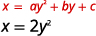 |
|
| منذ ذلك الحين\(a=2\)، ينفتح المكافئ على اليمين. | |
 |
|
| للعثور على محور التماثل، ابحث\(y=-\dfrac{b}{2 a}\) | \(y=-\dfrac{b}{2 a}\) |
| \(y=-\dfrac{0}{2(2)}\) | |
| \(y=0\) | |
| محور التماثل هو\(y=0\). | |
| قمة الرأس على الخط\(y=0\). | \(x=2 y^{2}\) |
| دعونا\(y=0\). |  |
| \(x=0\) | |
| قمة الرأس هي\((0,0)\). |
نظرًا لوجود قمة الرأس\((0,0)\)، فإن كلا من\(x\) - و\(y\) -المعترضين هما النقطة\((0,0)\). لرسم المكافئ نحتاج إلى المزيد من النقاط. في هذه الحالة، يكون من الأسهل اختيار قيم\(y\).
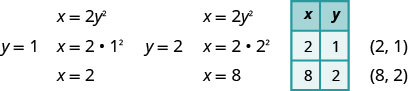
نرسم أيضًا النقاط المتماثلة مع\((2,1)\)\(y\) المحور -وعبره، النقاط\((2,−1),(8,−2)\).\((8,2)\)
رسم بياني للقطع المكافئ.
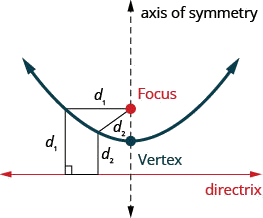
رسم بياني\(x=y^{2}\) باستخدام الخصائص.
- إجابة
-
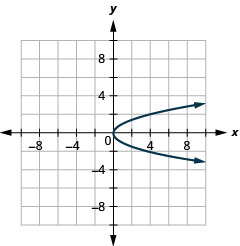
الشكل 11.2.40
رسم بياني\(x=-y^{2}\) باستخدام الخصائص.
- إجابة
-
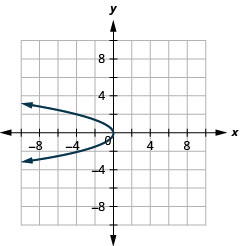
الشكل 11.2.41
في المثال التالي، لا تكون قمة الرأس هي الأصل.
رسم بياني\(x=-y^{2}+2 y+8\) باستخدام الخصائص.
الحل:
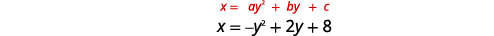 |
|
| منذ ذلك الحين\(a=-1\)، يفتح القطع المكافئ على اليسار. | |
 |
|
| للعثور على محور التماثل، ابحث\(y=-\dfrac{b}{2 a}\) |
\(y=-\dfrac{b}{2 a}\) |
| \(y=-\dfrac{2}{2(-1)}\) | |
| \(y=1\) | |
| محور التماثل هو\(y=1\). | |
| قمة الرأس على الخط\(y=1\). | \(x=-y^{2}+2 y+8\) |
| دعونا\(y=1\). | 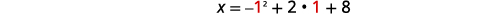 |
| \(x=9\) | |
| قمة الرأس هي\((9,1)\). | |
| يحدث\(x\) التقاطع عند حدوث ذلك\(y=0\). | \(x=-y^{2}+2 y+8\) |
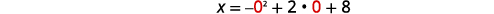 |
|
| \(x=8\) | |
| \(x\)التقاطع هو\((8,0)\). | |
| النقطة\((8,0)\) هي وحدة واحدة تحت خط التماثل. النقطة المتماثلة التي تقع فوق خط التماثل بوحدة واحدة هي\((8,2)\) |
النقطة المتماثلة هي\((8,2)\). |
| يحدث\(y\) التقاطع عند حدوث ذلك\(x=0\). | \(x=-y^{2}+2 y+8\) |
| بديل\(x=0\). | \(0=-y^{2}+2 y+8\) |
| حل. | \(y^{2}-2 y-8=0\) |
| \((y-4)(y+2)=0\) | |
| \(y=4, \quad y=-2\) | |
| \(y\)عمليات الاعتراض - هي\((0,4)\) و\((0,-2)\). | |
| قم بتوصيل النقاط لرسم القطع المكافئ. | 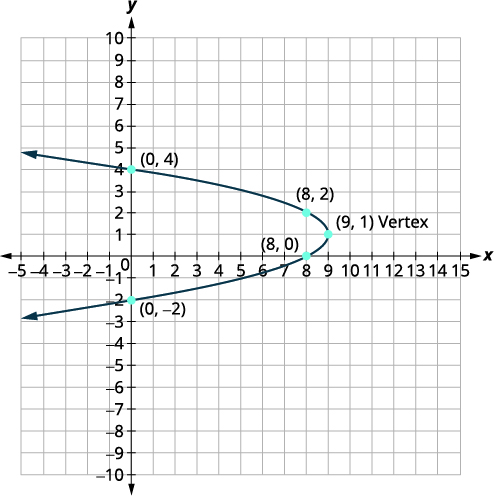 |
رسم بياني\(x=-y^{2}-4 y+12\) باستخدام الخصائص.
- إجابة
-
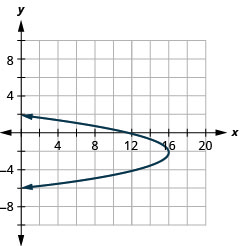
الشكل 11.2.58
رسم بياني\(x=-y^{2}+2 y-3\) باستخدام الخصائص.
- إجابة
-
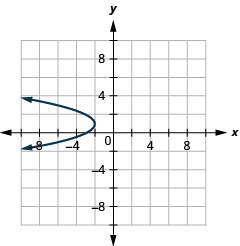
الشكل 11.2.59
في الجدول 11.2.4، نرى العلاقة بين المعادلة في الشكل القياسي وخصائص القطع المكافئ. يسرد مربع How To خطوات رسم المكافئ بيانيًا في النموذج القياسي\(x=a(y-k)^{2}+h\). سنستخدم هذا الإجراء في المثال التالي.
رسم بياني\(x=2(y-2)^{2}+1\) باستخدام الخصائص.
الحل:
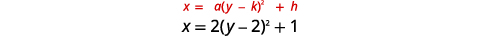 |
|
| حدد الثوابت\(a, h, k\). | \(a=2, h=1, k=2\) |
| منذ ذلك الحين\(a=2\)، ينفتح المكافئ على اليمين. | |
 |
|
| محور التماثل هو\(y=k\). | محور التماثل هو\(y=2\). |
| قمة الرأس هي\((h,k)\). | قمة الرأس هي\((1,2)\). |
| ابحث عن\(x\) التقاطع -عن طريق الاستبدال\(y=0\). | \(x=2(y-2)^{2}+1\) \(x=2(0-2)^{2}+1\) \(x=9\) |
| \(x\)التقاطع هو\((9,0)\). | |
| ابحث عن النقطة المتماثلة\((9,0)\) لعبور محور التماثل. | \((9,4)\) |
| ابحث عن\(y\) -Intercepts. دعونا\(x=0\). | \(\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}\) |
| لا يمكن أن يكون المربع سالبًا، لذلك لا يوجد حل حقيقي. لذلك لا\(y\) توجد اعتراضات. | |
| رسم بياني للقطع المكافئ. | 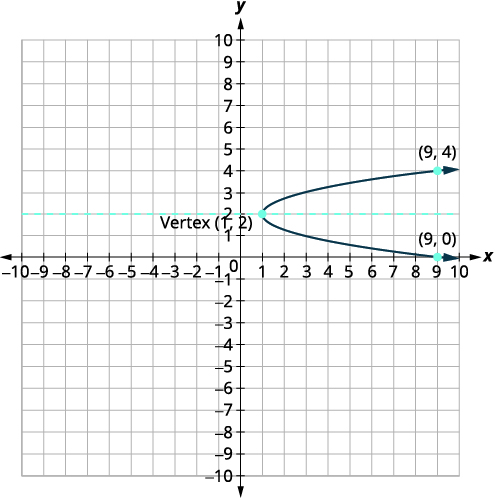 |
رسم بياني\(x=3(y-1)^{2}+2\) باستخدام الخصائص.
- إجابة
-
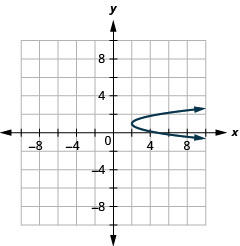
الشكل 11.2.63
رسم بياني\(x=2(y-3)^{2}+2\) باستخدام الخصائص.
- إجابة
-
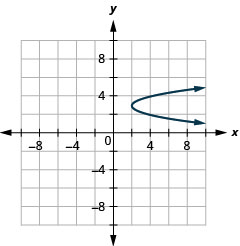
الشكل 11.2.64
في المثال التالي، نلاحظ أن a سالب وبالتالي يتم فتح القطع المكافئ إلى اليسار.
رسم بياني\(x=-4(y+1)^{2}+4\) باستخدام الخصائص.
الحل:
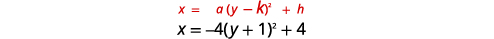 |
|
| حدد الثوابت\(a, h, k\). | \(a=-4, h=4, k=-1\) |
| منذ ذلك الحين\(a=-4\)، يفتح القطع المكافئ على اليسار. | |
 |
|
| محور التماثل هو\(y=k\). | محور التماثل هو\(y=-1\). |
| قمة الرأس هي\((h,k)\). | قمة الرأس هي\((4,-1)\). |
| ابحث عن\(x\) التقاطع -عن طريق الاستبدال\(y=0\). | \(x=-4(y+1)^{2}+4\) \(x=-4(0+1)^{2}+4\) \(x=0\) |
| \(x\)التقاطع هو\((0,0)\). | |
| ابحث عن النقطة المتماثلة\((0,0)\) لعبور محور التماثل. | \((0,-2)\) |
| ابحث عن\(y\) -Intercepts. | \(x=-4(y+1)^{2}+4\) |
| دعونا\(x=0\). | \(\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}\) |
| \(y=-1+1 \quad y=-1-1\) | |
| \(y=0 \quad\quad y=-2\) | |
| \(y\)عمليات الاعتراض - هي\((0,0)\) و\((0,-2)\). | |
| رسم بياني للقطع المكافئ. | 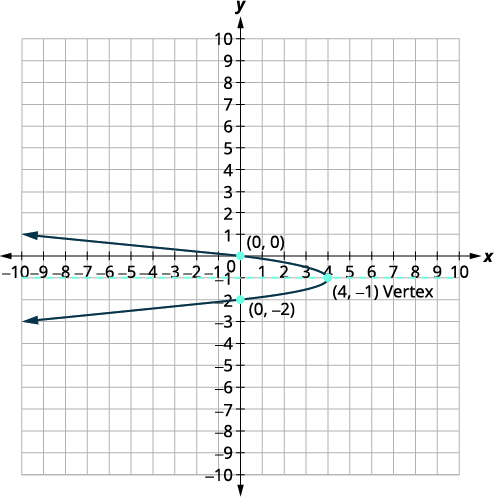 |
رسم بياني\(x=-4(y+2)^{2}+4\) باستخدام الخصائص.
- إجابة
-
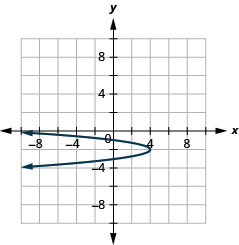
الشكل 11.2.68
رسم بياني\(x=-2(y+3)^{2}+2\) باستخدام الخصائص.
- إجابة
-
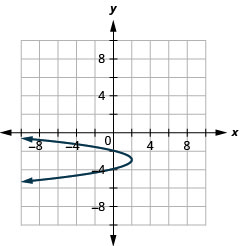
الشكل 11.2.69
يتطلب المثال التالي أن نضع المعادلة أولاً في النموذج القياسي ثم نستخدم الخصائص.
اكتب\(x=2 y^{2}+12 y+17\) في النموذج القياسي ثم استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
الحل:
| \(x=2 y^{2}+12 y+17\) | |
| أعد كتابة الدالة في\(x=a(y-k)^{2}+h\) الشكل بإكمال المربع. | \(x=2\left(y^{2}+6 y\right)+17\) |
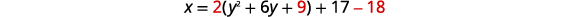 |
|
| \(x=2(y+3)^{2}-1\) | |
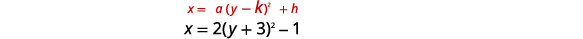 |
|
| حدد الثوابت\(a, h, k\). | \(a=2, h=-1, k=-3\) |
| منذ ذلك الحين\(a=2\)، ينفتح المكافئ على اليمين. | |
 |
|
| محور التماثل هو\(y=k\). | محور التماثل هو\(y=-3\). |
| قمة الرأس هي\((h,k)\). | قمة الرأس هي\((-1,-3)\). |
| ابحث عن\(x\) التقاطع -عن طريق الاستبدال\(y=0\). | \(x=2(y+3)^{2}-1\) \(x=2(0+3)^{2}-1\) \(x=17\) |
| \(x\)التقاطع هو\((17,0)\). | |
| ابحث عن النقطة المتماثلة\((17,0)\) لعبور محور التماثل. | \((17,-6)\) |
|
ابحث عن\(y\) -Intercepts. دعونا\(x=0\). |
\(\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}\) |
| \(y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}\) | |
| \(y \approx-2.3 \quad y \approx-3.7\) | |
| \(y\)عمليات الاعتراض الإلكترونية هي\(\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)\). | |
| رسم بياني للقطع المكافئ. | 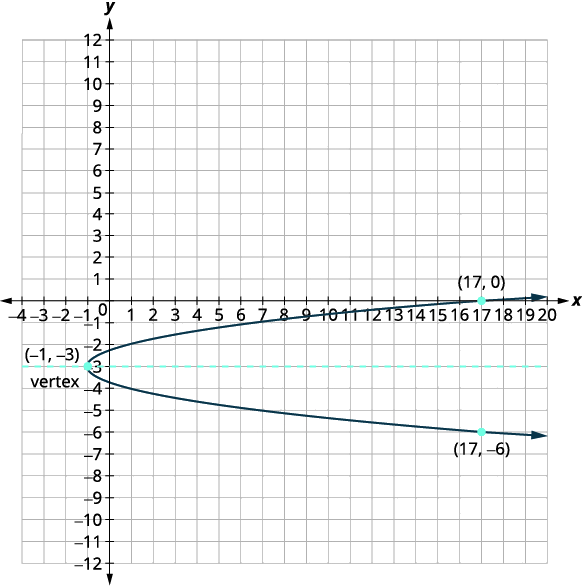 |
- اكتب\(x=3 y^{2}+6 y+7\) في النموذج القياسي و
- استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
- إجابة
-
- \(x=3(y+1)^{2}+4\)
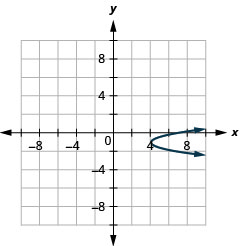
الشكل 11.2.77
- اكتب\(x=-4 y^{2}-16 y-12\) في النموذج القياسي و
- استخدم خصائص النموذج القياسي لرسم المعادلة بيانيًا.
- إجابة
-
- \(x=-4(y+2)^{2}+4\)
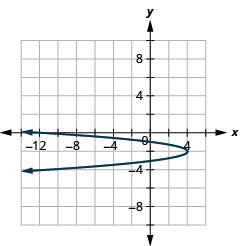
الشكل 11.2.78
حل التطبيقات باستخدام Parabolas
تتضمن العديد من التصميمات المعمارية بارابولاس. ليس من غير المألوف أن يتم بناء الجسور باستخدام parabolas كما سنرى في المثال التالي.
أوجد معادلة القوس المكافئ المتكوَّن في أساس الجسر الموضَّح. اكتب المعادلة في الصورة القياسية.
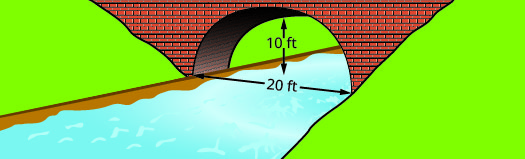
الحل:
سنقوم أولاً بإعداد نظام الإحداثيات ورسم القطع المكافئ. سيعطينا الرسم البياني المعلومات التي نحتاجها لكتابة معادلة الرسم البياني في النموذج القياسي\(y=a(x-h)^{2}+k\).
|
اجعل الجانب الأيسر السفلي من الجسر هو أصل شبكة الإحداثيات عند النقطة\((0,0)\). نظرًا لأن القاعدة بعرض\(20\) قدم، فإن النقطة\((20,0)\) تمثل الجانب الأيمن السفلي. يبلغ ارتفاع الجسر 10 أقدام عند أعلى نقطة. أعلى نقطة هي قمة المكافئ، لذا سيكون\(y\) |
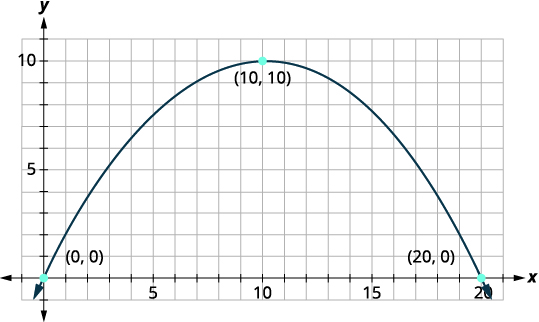 |
| تحديد قمة الرأس،\((h,k)\). | \((h, k)=(10,10)\) |
| \(h=10, \quad k=10\) | |
|
استبدل القيم في النموذج القياسي. لا تزال قيمة\(a\) الـ غير معروفة. للعثور على قيمة\(a\) استخدام إحدى النقاط الأخرى على القطع المكافئ. |
\(\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}\) |
| استبدل قيم النقطة الأخرى في المعادلة. | \(y=a(x-10)^{2}+10\) \(0=a(0-10)^{2}+10\) |
| حل لـ\(a\). | \(\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}\) |
| \(y=a(x-10)^{2}+10\) | |
| استبدل القيمة بـ\(a\) في المعادلة. | \(y=-\dfrac{1}{10}(x-10)^{2}+10\) |
أوجد معادلة القوس المكافئ المتكوَّن في أساس الجسر الموضَّح. اكتب المعادلة في الصورة القياسية.
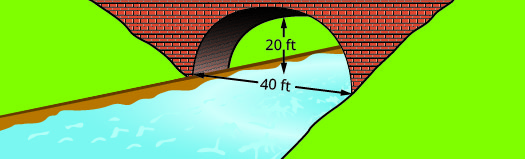
- إجابة
-
\(y=-\dfrac{1}{20}(x-20)^{2}+20\)
أوجد معادلة القوس المكافئ المتكوَّن في أساس الجسر الموضَّح. اكتب المعادلة في الصورة القياسية.
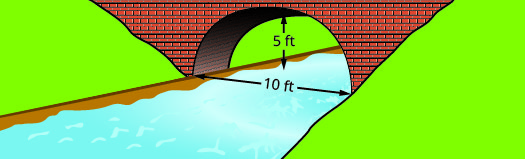
- إجابة
-
\(y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام الوظائف التربيعية والممثلات.
- الدوال التربيعية
- مقدمة إلى القصص المخروطية ورسم الأشكال الجانبية الأفقية
المفاهيم الرئيسية
- بارابولا: المكافئ هو جميع النقاط في المستوى التي تكون على نفس المسافة من نقطة ثابتة وخط ثابت. تسمى النقطة الثابتة بالتركيز، والخط الثابت يسمى دليل المكافئ.
بارابولاس عمودية
|
نموذج عام \(y=a x^{2}+b x+c\) |
نموذج قياسي \(y=a(x-h)^{2}+k\) |
|
|---|---|---|
| اتجاه | \ (y=a x^ {2} +b x+c\) ">\(a>0\) لأعلى؛\(a<0\) لأسفل | \ (y=a (x-h) ^ {2} +k\) ">\(a>0\) لأعلى؛\(a<0\) لأسفل |
| محور التماثل | \ (y=a x^ {2} +ب x+c\) ">\(x=-\dfrac{b}{2 a}\) | \ (y=a (x-h) ^ {2} +k\) ">\(x=h\) |
| فيرتكس | \ (y=a x^ {2} +b x+c\) ">بديل\(x=-\dfrac{b}{2 a}\) وحل لـ\(y .\) |
\ (y=a (x-h) ^ {2} +k\) ">\((h, k)\) |
| \(y\)-اعتراض | \ (y=a x^ {2} +ب x+c\) ">Let\(x=0\) | \ (y=a (x-h) ^ {2} +k\) ">دع\(x=0\) |
| \(x\)- عمليات الاعتراض | \ (y=a x^ {2} +ب x+c\) ">Let\(y=0\) | \ (y=a (x-h) ^ {2} +k\) ">دع\(y=0\) |
- كيفية رسم بياني للبارابولاس الرأسية\(y=a x^{2}+b x+c\) أو\(f(x)=a(x-h)^{2}+k)\) استخدام الخصائص.
- حدِّد ما إذا كان القطع المكافئ ينفتح لأعلى أم لأسفل.
- أوجد محور التماثل.
- ابحث عن قمة الرأس.
- ابحث\(y\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(y\) المقطوع عبر محور التماثل.
- ابحث عن\(x\) -Intercepts.
- رسم بياني للقطع المكافئ.
بارابولاس أفقية
|
نموذج عام \(x=a y^{2}+b y+c\) |
نموذج قياسي \(x=a(y-k)^{2}+h\) |
|
|---|---|---|
| اتجاه | \ (x=a y^ {2} +b y+c\) ">\(a>0\) اليمين؛\(a<0\) اليسار | \ (x=a (y-k) ^ {2} +h\) ">\(a>0\) اليمين؛\(a<0\) اليسار |
| محور التماثل | \ (x=a y^ {2} +b y+c\) ">\(y=-\dfrac{b}{2 a}\) | \ (x=a (y-k) ^ {2} +h\) ">\(y=k\) |
| فيرتكس | \ (x=a y^ {2} +b y+c\) ">بديل\(y=-\dfrac{b}{2 a}\) وحل لـ\(x .\) |
\ (x=a (y-k) ^ {2} +h\) ">\((h, k)\) |
| \(x\)- عمليات الاعتراض | \ (x=a y^ {2} +b y+c\) ">Let\(x=0\) | \ (x=a (y-k) ^ {2} +h\) ">Let\(x=0\) |
| \(y\)-اعتراض | \ (x=a y^ {2} +b y+c\) ">Let\(y=0\) | \ (x=a (y-k) ^ {2} +h\) ">Let\(y=0\) |

كيفية رسم الأشكال الأفقية للرسم البياني\(x=a y^{2}+b y+c\) أو\(x=a(y-k)^{2}+h\) استخدام الخصائص.
- حدِّد ما إذا كان القطع المكافئ ينفتح على اليسار أم إلى اليمين.
- أوجد محور التماثل.
- ابحث عن قمة الرأس.
- ابحث\(x\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(x\) المقطوع عبر محور التماثل.
- ابحث عن\(y\) -Intercepts.
- رسم بياني للقطع المكافئ.
مسرد المصطلحات
- المكافئ
- المكافئ هو كل النقاط في المستوى الذي يقع على نفس المسافة من نقطة ثابتة وخط ثابت.


