الفصل 10 تمارين المراجعة

تمارين مراجعة الفصل

إيجاد الدوال المركَّبة والعكسية

التمارين$\PageIndex{1}$ Find and Evaluate Composite Functions

في التمارين التالية، لكل زوج من الوظائف، ابحث

1. $(f \circ g)(x)$
2. $(g \circ f)(x)$
3. $(f \cdot g)(x)$

1. $f(x)=7 x-2$و$g(x)=5 x+1$

2. $f(x)=4 x$و$g(x)=x^{2}+3 x$

إجابة

2.

1. $4 x^{2}+12 x$
2. $16 x^{2}+12 x$
3. $4 x^{3}+12 x^{2}$

التمارين$\PageIndex{2}$ Find and Evaluate Composite Functions

في التمارين التالية، قم بتقييم التركيبة.

1. للوظائف$f(x)=3 x^{2}+2$ وابحث$g(x)=4 x-3$
   1. $(f \circ g)(-3)$
   2. $(g \circ f)(-2)$
   3. $(f \circ f)(-1)$
2. للوظائف$f(x)=2 x^{3}+5$ وابحث$g(x)=3 x^{2}-7$
   1. $(f \circ g)(-1)$
   2. $(g \circ f)(-2)$
   3. $(g \circ g)(1)$

إجابة

2.

1. $-123$
2. $356$
3. $41$

التمارين$\PageIndex{3}$ Determine Whether a Function is One-to-One

في التمارين التالية، بالنسبة لكل مجموعة من الأزواج المرتبة، حدد ما إذا كانت تمثل دالة أم لا، وإذا كان الأمر كذلك، فهي الدالة 1 إلى 1.

1. $\begin{array}{l}{\{(-3,-5),(-2,-4),(-1,-3),(0,-2)} , {(-1,-1),(-2,0),(-3,1) \}}\end{array}$
2. $\begin{array}{l}{\{(-3,0),(-2,-2),(-1,0),(0,1)} , {(1,2),(2,1),(3,-1) \}}\end{array}$
3. $\begin{array}{l}{\{(-3,3),(-2,1),(-1,-1),(0,-3)} , {(1,-5),(2,-4),(3,-2) \}}\end{array}$

إجابة

2. الوظيفة؛ ليست واحدة لواحد

التمارين$\PageIndex{4}$ Determine Whether a Function is One-to-One

في التمارين التالية، حدد ما إذا كان كل رسم بياني يمثل رسمًا بيانيًا لدالة، وإذا كان الأمر كذلك، فهل هو رسم بياني لواحد.

1. 1. 
      
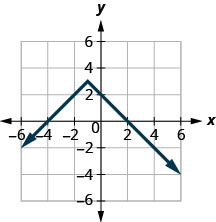
      الشكل 10-هاء-1
   2. 
      
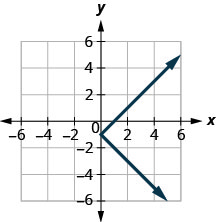
      الشكل 10-هاء-2
2. 1. 
      
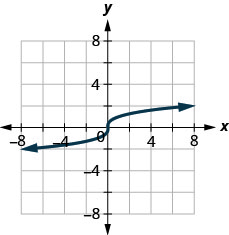
      الشكل 10-هاء-3
   2. 
      
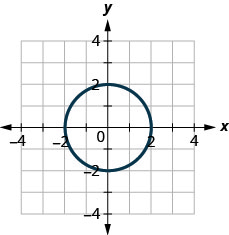
      الشكل 10-هاء-4

إجابة

1.

1. الوظيفة؛ ليست واحدة لواحد
2. ليست وظيفة

التمارين$\PageIndex{5}$ Find the Inverse of a Function

في التمرين التالي، ابحث عن معكوس الدالة. حدِّد مجال ومدى الدالة العكسية.

1. $\{(-3,10),(-2,5),(-1,2),(0,1)\}$

إجابة

1. دالة عكسية:$\{(10,-3),(5,-2),(2,-1),(1,0)\}$. اسم النطاق:$\{1,2,5,10\}$. النطاق:$\{-3,-2,-1,0\}$.

التمارين$\PageIndex{6}$ Find the Inverse of a Function

في التمرين التالي، قم برسم معكوس دالة واحد إلى واحد كما هو موضح.

الشكل 10-هاء-5

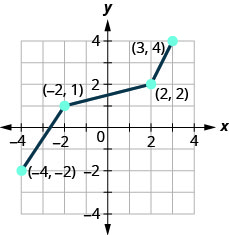
إجابة

قم بحل المشكلة بنفسك

التمارين$\PageIndex{7}$ Find the Inverse of a Function

في التمارين التالية، تحقق من أن الدوال هي دوال عكسية.

1. $\begin{array}{l}{f(x)=3 x+7 \text { and }} {g(x)=\frac{x-7}{3}}\end{array}$
2. $\begin{array}{l}{f(x)=2 x+9 \text { and }} {g(x)=\frac{x+9}{2}}\end{array}$

إجابة

1. $g(f(x))=x,$$f(g(x))=x,$وبالتالي فهي معكوسة.

التمارين$\PageIndex{8}$ Find the Inverse of a Function

1. $f(x)=6 x-11$
2. $f(x)=x^{3}+13$
3. $f(x)=\frac{1}{x+5}$
4. $f(x)=\sqrt[5]{x-1}$

إجابة

1. $f^{-1}(x)=\frac{x+11}{6}$

3. $f^{-1}(x)=\frac{1}{x}-5$

إيجاد قيمة الدالة الأسية وتمثيلها

التمارين$\PageIndex{9}$ Graph Exponential Functions

في التمارين التالية، قم برسم بياني لكل وظيفة من الوظائف التالية.

1. $f(x)=4^{x}$
2. $f(x)=\left(\frac{1}{5}\right)^{x}$
3. $g(x)=(0.75)^{x}$
4. $g(x)=3^{x+2}$
5. $f(x)=(2.3)^{x}-3$
6. $f(x)=e^{x}+5$
7. $f(x)=-e^{x}$

إجابة

1.

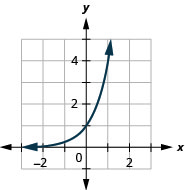
الشكل 10 هاء -6

3.

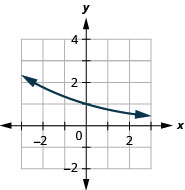
الشكل 10 هاء - 7

5.

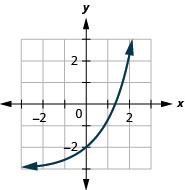
الشكل 10 هاء -8

7.

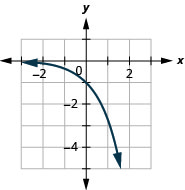
الشكل 10 هاء - 9

التمارين$\PageIndex{10}$ Solve Exponential Equations

في التمارين التالية، قم بحل كل معادلة.

1. $3^{5 x-6}=81$
2. $2^{x^{2}}=16$
3. $9^{x}=27$
4. $5^{x^{2}+2 x}=\frac{1}{5}$
5. $e^{4 x} \cdot e^{7}=e^{19}$
6. $\frac{e^{x^{2}}}{e^{15}}=e^{2 x}$

إجابة

2. $x=-2, x=2$

4. $x=-1$

6. $x=-3, x=5$

التمارين$\PageIndex{11}$ Use Exponential Models in Applications

في التمارين التالية، قم بحل.

1. استثمر فيليكس $$12,000$ في حساب التوفير. إذا كان معدل الفائدة هو$4$% كم سيكون في الحساب$12$ بالسنوات بكل طريقة من طرق التجميع؟
   1. مجمع ربع سنوي
   2. مجمع شهري
   3. مركب بشكل مستمر
2. يقوم سيد بإيداع $$20,000$ في حساب استثماري. ماذا ستكون قيمة استثماره في$30$ السنوات إذا كان الاستثمار يكسب$7$ نسبة مئوية سنويًا ويتفاقم بشكل مستمر؟
3. يدرس باحث في مركز السيطرة على الأمراض والوقاية منها نمو البكتيريا. تبدأ تجربتها مع$150$ البكتيريا التي تنمو بمعدل$15$% في الساعة. ستفحص البكتيريا كل$24$ ساعة. كم عدد البكتيريا التي سيجدها في$24$ ساعات؟
4. في السنوات الخمس الماضية، نما عدد سكان الولايات المتحدة بمعدل$0.7$% سنويًا إلى حوالي$318,900,000$. إذا استمر هذا المعدل، فماذا سيكون عدد السكان في سنوات$5$ أخرى؟

إجابة

2. $\$ 163,323.40$

4. $330,259,000$

إيجاد قيم الدوال اللوغاريتمية ورسمها

التمارين$\PageIndex{12}$ Convert Between Exponential and Logarithmic Form

في التمارين التالية، قم بالتحويل من الصورة الأسية إلى الصورة اللوغاريتمية.

1. $5^{4}=625$
2. $10^{-3}=\frac{1}{1,000}$
3. $63^{\frac{1}{5}}=\sqrt[5]{63}$
4. $e^{y}=16$

إجابة

2. $\log \frac{1}{1,000}=-3$

4. $\ln 16=y$

التمارين$\PageIndex{13}$ Convert Between Exponential and Logarithmic Form

في التمارين التالية، قم بتحويل كل معادلة لوغاريتمية إلى صورة أسية.

1. $7=\log _{2} 128$
2. $5=\log 100,000$
3. $4=\ln x$

إجابة

2. $100000=10^{5}$

التمارين$\PageIndex{14}$ Evaluate Logarithmic Functions

في التمارين التالية، قم بحل المشكلة$x$.

1. $\log _{x} 125=3$
2. $\log _{7} x=-2$
3. $\log _{\frac{1}{2}} \frac{1}{16}=x$

إجابة

1. $x=5$

3. $x=4$

التمارين$\PageIndex{15}$ Evaluate Logarithmic Functions

في التمارين التالية، ابحث عن القيمة الدقيقة لكل لوغاريتم بدون استخدام الآلة الحاسبة.

1. $\log _{2} 32$
2. $\log _{8} 1$
3. $\log _{3} \frac{1}{9}$

إجابة

2. $0$

التمارين$\PageIndex{16}$ Graph Logarithmic Functions

في التمارين التالية، قم برسم بياني لكل دالة لوغاريتمية.

1. $y=\log _{5} x$
2. $y=\log _{\frac{1}{4}} x$
3. $y=\log _{0.8} x$

إجابة

1.

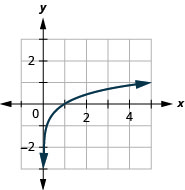
الشكل 10 هاء -10

3.

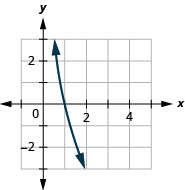
الشكل 10 هاء -11

التمارين$\PageIndex{17}$ Solve Logarithmic Equations

في التمارين التالية، قم بحل كل معادلة لوغاريتمية.

1. $\log _{a} 36=5$
2. $\ln x=-3$
3. $\log _{2}(5 x-7)=3$
4. $\ln e^{3 x}=24$
5. $\log \left(x^{2}-21\right)=2$

إجابة

2. $x=e^{-3}$

4. $x=8$

التمارين$\PageIndex{18}$ Use Logarithmic Models in Applications

ما مستوى الديسيبل لصافرة قطار بكثافة$10^{−3}$ الواط لكل بوصة مربعة؟

إجابة

$90$ديسيبل

استخدم خصائص اللوغاريتمات

التمارين$\PageIndex{19}$ Use the Properties of Logarithms

في التمارين التالية، استخدم خصائص اللوغاريتمات للتقييم.

1. 1. $\log _{7} 1$
   2. $\log _{12} 12$
2. 1. $5^{\log _{5} 13}$
   2. $\log _{3} 3^{-9}$
3. 1. $10^{\log \sqrt{5}}$
   2. $\log 10^{-3}$
4. 1. $e^{\ln 8}$
   2. $\ln e^{5}$

إجابة

2.

1. $13$
2. $-9$

4.

1. $8$
2. $5$

التمارين$\PageIndex{20}$ Use the Properties of Logarithms

في التمارين التالية، استخدم خاصية المنتج للوغاريتمات لكتابة كل لوغاريتم في صورة مجموع اللوغاريتمات. قم بالتبسيط إن أمكن.

1. $\log _{4}(64 x y)$
2. $\log 10,000 m$

إجابة

2. $4+\log m$

التمارين$\PageIndex{21}$ Use the Properties of Logarithms

في التمارين التالية، استخدم خاصية حاصل القسمة للوغاريتمات لكتابة كل لوغاريتم في صورة مجموع اللوغاريتمات. قم بالتبسيط، إن أمكن.

1. $\log _{7} \frac{49}{y}$
2. $\ln \frac{e^{5}}{2}$

إجابة

2. $5-\ln 2$

التمارين$\PageIndex{22}$ Use the Properties of Logarithms

في التمارين التالية، استخدم خاصية قوة اللوغاريتمات لتوسيع كل لوغاريتم. قم بالتبسيط، إن أمكن.

1. $\log x^{-9}$
2. $\log _{4} \sqrt[7]{z}$

إجابة

2. $\frac{1}{7} \log _{4} z$

التمارين$\PageIndex{23}$ Use the Properties of Logarithms

في التمارين التالية، استخدم خصائص اللوغاريتمات لكتابة كل لوغاريتم في صورة مجموع اللوغاريتمات. قم بالتبسيط إن أمكن.

1. $\log _{3}\left(\sqrt{4} x^{7} y^{8}\right)$
2. $\log _{5} \frac{8 a^{2} b^{6} c}{d^{3}}$
3. $\ln \frac{\sqrt{3 x^{2}-y^{2}}}{z^{4}}$
4. $\log _{6} \sqrt[3]{\frac{7 x^{2}}{6 y^{3} z^{5}}}$

إجابة

2. $\begin{array}{l}{\log _{5} 8+2 \log _{5} a+6 \log _{5} b} {+\log _{5} c-3 \log _{5} d}\end{array}$

4. $\begin{array}{l}{\frac{1}{3}\left(\log _{6} 7+2 \log _{6} x-1-3 \log _{6} y\right.} {-5 \log _{6} z )}\end{array}$

التمارين$\PageIndex{24}$ Use the Properties of Logarithms

في التمارين التالية، استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم. قم بالتبسيط إن أمكن.

1. $\log _{2} 56-\log _{2} 7$
2. $3 \log _{3} x+7 \log _{3} y$
3. $\log _{5}\left(x^{2}-16\right)-2 \log _{5}(x+4)$
4. $\frac{1}{4} \log y-2 \log (y-3)$

إجابة

2. $\log _{3} x^{3} y^{7}$

4. $\log \frac{\sqrt[4]{y}}{(y-3)^{2}}$

التمارين$\PageIndex{25}$ Use the Change-of-Base Formula

في التمارين التالية، بالتقريب إلى ثلاث منازل عشرية، قم بتقريب كل لوغاريتم تقريبًا.

1. $\log _{5} 97$
2. $\log _{\sqrt{3}} 16$

إجابة

2. $5.047$

حل المعادلات الأسية واللوغاريتمية

التمارين$\PageIndex{26}$ Solve Logarithmic Equations Using the Properties of Logarithms

في التمارين التالية، قم بحل المشكلة$x$.

1. $3 \log _{5} x=\log _{5} 216$
2. $\log _{2} x+\log _{2}(x-2)=3$
3. $\log (x-1)-\log (3 x+5)=-\log x$
4. $\log _{4}(x-2)+\log _{4}(x+5)=\log _{4} 8$
5. $\ln (3 x-2)=\ln (x+4)+\ln 2$

إجابة

2. $x=4$

4. $x=3$

التمارين$\PageIndex{27}$ Solve Exponential Equations Using Logarithms

في التمارين التالية، حل كل معادلة أسية. ابحث عن الإجابة الصحيحة ثم قربها إلى ثلاث منازل عشرية.

1. $2^{x}=101$
2. $e^{x}=23$
3. $\left(\frac{1}{3}\right)^{x}=7$
4. $7 e^{x+3}=28$
5. $e^{x-4}+8=23$

إجابة

1. $x=\frac{\log 101}{\log 2} \approx 6.658$

3. $x=\frac{\log 7}{\log \frac{1}{3}} \approx-1.771$

5. $x=\ln 15+4 \approx 6.708$

التمارين$\PageIndex{28}$ Use Exponential Models in Applications

1. جيروم يستثمر $$18,000$ في العمر$17$. يأمل أن تبلغ قيمة الاستثمارات $$30,000$ عندما يتحول$26$. إذا كانت الفائدة تتزايد باستمرار، فما معدل النمو الذي سيحتاجه تقريبًا لتحقيق هدفه؟ هل هذا توقع معقول؟
2. تستثمر إليز دولارًا$4500$ في حساب يضاعف الفائدة شهريًا ويكسب$6$ %.كم من الوقت ستستغرق مضاعفة أموالها؟
3. سجل الباحثون أن عددًا معينًا من البكتيريا نما من$100$ إلى$300$ في$8$ ساعات. عند معدل النمو هذا، كم عدد البكتيريا التي ستكون موجودة في$24$ غضون ساعات؟
4. يمكن أن تتضاعف أعداد الماوس في$8$ الأشهر$\left(A=2 A_{0}\right)$. كم من الوقت سيستغرق عدد الفئران ثلاثة أضعاف؟
5. عمر النصف لليود المشع هو$60$ أيام. ما مقدار عينة$50$ الملجم المتبقية في$40$ الأيام؟

إجابة

2. $11.6$سنوات

4. $12.7$أشهر

اختبار الممارسة

التمارين$\PageIndex{29}$

1. للوظائف$g(x)=8x−3$،$f(x)=6x+1$ وابحث
   1. $(f \circ g)(x)$
   2. $(g \circ f)(x)$
   3. $(f \cdot g)(x)$
2. حدد ما إذا كانت المجموعة التالية من الأزواج المرتبة تمثل دالة أم لا، وإذا كان الأمر كذلك، فهي الدالة من واحد إلى واحد. $\{(-2,2),(-1,-3),(0,1),(1,-2),(2,-3)\}$
3. حدِّد هل كل رسم بياني يمثل رسمًا بيانيًا لدالة، وإذا كان الأمر كذلك، فهل هو رسم بياني لدالة
   1. 
      
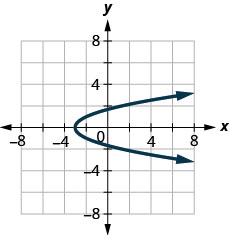
      الشكل 10 هاء - 12
   2. 
      
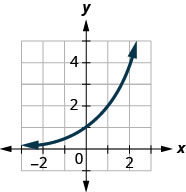
      الشكل 10 هاء - 13
4. رسم بياني، على نفس النظام الإحداثي، يظهر معكوس الدالة الفردية.

الشكل 10 هاء - 14

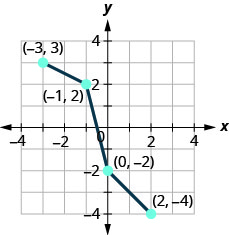
5. أوجد معكوس الدالة$f(x)=x^{5}−9$.

6. رسم بياني للدالة$g(x)=2^{x-3}$.

7. حل المعادلة$2^{2 x-4}=64$.

8. حل المعادلة$\frac{e^{x^{2}}}{e^{4}}=e^{3 x}$.

9. استثمرت ميغان $$21,000$ في حساب التوفير. إذا كان معدل الفائدة هو$5$%، فكم سيكون في الحساب$8$ بالسنوات حسب كل طريقة من طرق التجميع؟

1. مجمع ربع سنوي
2. مجمع شهري
3. مركب بشكل مستمر

10. حوِّل المعادلة من الصورة الأسية إلى الصورة اللوغاريتمية:$10^{-2}=\frac{1}{100}$.

11. حوِّل المعادلة من المعادلة اللوغاريتمية إلى الصورة الأسية:$3=\log _{7} 343$.

12. حل لـ$x$:$\log _{5} x=-3$

13. سجل التقييم$_{11} 1$.

14. تقييم$\log _{4} \frac{1}{64}$.

15. رسم بياني للدالة$y=\log _{3} x$.

16. حل لـ$x$:$\log \left(x^{2}-39\right)=1$

17. ما مستوى الديسيبل لمروحة صغيرة بكثافة$10^{−8}$ الواط لكل بوصة مربعة؟

18. قم بتقييم كل منها.

1. $6^{\log _{6} 17}$
2. $\log _{9} 9^{-3}$

إجابة

1.

1. $48 x-17$
2. $48 x+5$
3. $48 x^{2}-10 x-3$

3.

1. ليست وظيفة
2. وظيفة واحدة إلى واحدة

5. $f^{-1}(x)=\sqrt[5]{x+9}$

7. $x=5$

9.

1. $$31,250.74$
2. $$31,302.29$
3. $$31,328.32$

11. $343=7^{3}$

13. $0$

15.

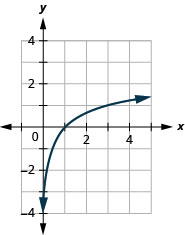
الشكل 10 هاء - 15

17. $40$ديسيبل

التمارين$\PageIndex{30}$

في التمارين التالية، استخدم خصائص اللوغاريتمات لكتابة كل تعبير كمجموع اللوغاريتمات، مع التبسيط إن أمكن.

1. $\log _{5} 25 a b$
2. $\ln \frac{e^{12}}{8}$
3. $\log _{2} \sqrt[4]{\frac{5 x^{3}}{16 y^{2} z^{7}}}$

إجابة

1. $2+\log _{5} a+\log _{5} b$

3. $\begin{array}{l}{\frac{1}{4}\left(\log _{2} 5+3 \log _{2} x-4-2 \log _{2} y\right.} {-7 \log _{2} z )}\end{array}$

التمارين$\PageIndex{31}$

في التمارين التالية، استخدم خصائص اللوغاريتمات لتكثيف اللوغاريتم وتبسيطه إن أمكن.

1. $5 \log _{4} x+3 \log _{4} y$
2. $\frac{1}{6} \log x-3 \log (x+5)$
3. التقريب إلى ثلاث منازل عشرية، بشكل تقريبي$\log _{4} 73$.
4. حل لـ$x$:$\log _{7}(x+2)+\log _{7}(x-3)=\log _{7} 24$

إجابة

2. $\log \frac{\sqrt[6]{x}}{(x+5)^{3}}$

4. $x=6$

التمارين$\PageIndex{32}$

في التمارين التالية، حل كل معادلة أسية. ابحث عن الإجابة الصحيحة ثم قربها إلى ثلاث منازل عشرية.

1. $\left(\frac{1}{5}\right)^{x}=9$
2. $5 e^{x-4}=40$
3. يستثمر جاكوب $$14,000$ في حساب يضاعف الفائدة كل ثلاثة أشهر ويكسب$4$%. كم من الوقت سيستغرق مضاعفة أمواله؟
4. سجل الباحثون أن عددًا معينًا من البكتيريا نما من$500$ إلى$700$ في$5$ ساعات. عند معدل النمو هذا، كم عدد البكتيريا التي ستكون موجودة في$20$ غضون ساعات؟
5. يمكن أن تتضاعف أعداد خنفساء معينة في$3$ غضون أشهر$\left(A=2 A_{0}\right)$. كم من الوقت سيستغرق عدد هذه الخنافس ثلاث مرات؟

إجابة

2. $x=\ln 8+4 \approx 6.079$

4. $1,921$بكتيريا