9.9E: تمارين

Last updated
Save as PDF

Page ID: 201647

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

الممارسة تجعل من الكمال

التمارين الرياضية$\PageIndex{11}$ Solve Quadratic Inequalities Graphically

في التمارين التالية،

حل بشكل رسومي
اكتب الحل في الترميز الفاصل الزمني
1. $x^{2}+6 x+5>0$
2. $x^{2}+4 x-12<0$
3. $x^{2}+4 x+3 \leq 0$
4. $x^{2}-6 x+8 \geq 0$
5. $-x^{2}-3 x+18 \leq 0$
6. $-x^{2}+2 x+24<0$
7. $-x^{2}+x+12 \geq 0$
8. $-x^{2}+2 x+15>0$

إجابة

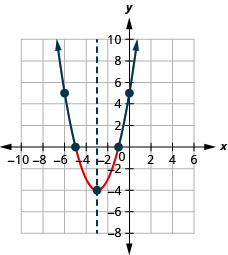
$الرسم البياني الموضح هو شكل مكافئ متجه لأعلى مع قمة الرأس (سالب 3، سالب 4) ونقطة تقاطع y (0,5).$
الشكل 9.8.16
$(-\infty,-5) \cup(-1, \infty)$

$الرسم البياني الموضح هو شكل مكافئ متجه لأعلى وله رأس (سالب 2، سالب 1) ونقطة تقاطع y (0,3).$
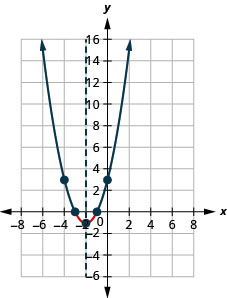
الشكل 9.8.17
$[-3,-1]$

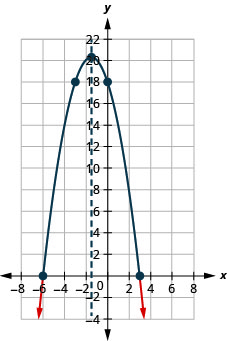
$الرسم البياني الموضح هو شكل مكافئ متجه لأسفل وله رأس (سالب 1 و5 أعشار، 20) ونقطة تقاطع y (0، 18).$
الشكل 9.8.18
$(-\infty,-6] \cup[3, \infty)$

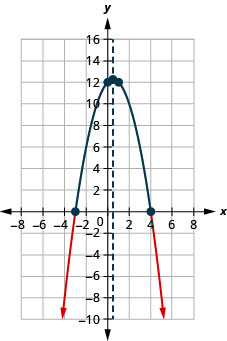
$الرسم البياني الموضح هو شكل مكافئ متجه لأسفل مع قطع تقاطع ص قدره (0، 12) وقطعه x (سالب 3، 0) و (4، 0).$
الشكل 9.8.19
$[-3,4]$

التمارين الرياضية$\PageIndex{12}$ Solve Quadratic Inequalities Graphically

في التمارين التالية، قم بحل كل متباينة جبريًا واكتب أي حل في شكل فاصل زمني.

$x^{2}+3 x-4 \geq 0$
$x^{2}+x-6 \leq 0$
$x^{2}-7 x+10<0$
$x^{2}-4 x+3>0$
$x^{2}+8 x>-15$
$x^{2}+8 x<-12$
$x^{2}-4 x+2 \leq 0$
$-x^{2}+8 x-11<0$
$x^{2}-10 x>-19$
$x^{2}+6 x<-3$
$-6 x^{2}+19 x-10 \geq 0$
$-3 x^{2}-4 x+4 \leq 0$
$-2 x^{2}+7 x+4 \geq 0$
$2 x^{2}+5 x-12>0$
$x^{2}+3 x+5>0$
$x^{2}-3 x+6 \leq 0$
$-x^{2}+x-7>0$
$-x^{2}-4 x-5<0$
$-2 x^{2}+8 x-10<0$
$-x^{2}+2 x-7 \geq 0$

إجابة

1. $(-\infty,-4] \cup[1, \infty)$

3. $(2,5)$

5. $(-\infty,-5) \cup(-3, \infty)$

7. $[2-\sqrt{2}, 2+\sqrt{2}]$

9. $(-\infty, 5-\sqrt{6}) \cup(5+\sqrt{6}, \infty)$

11. $\left(-\infty,-\frac{5}{2}\right] \cup\left[-\frac{2}{3}, \infty\right)$

13. $\left[-\frac{1}{2}, 4\right]$

15. $(-\infty, \infty)$

17. لا يوجد حل

19. $(-\infty, \infty)$

التمارين الرياضية$\PageIndex{13}$ Writing Exercises

اشرح النقاط الحرجة وكيفية استخدامها لحل المتباينات التربيعية جبريًا.
قم بحل$x^{2}+2x≥8$ كلًا من الناحية الرسومية والجبرية. ما الطريقة التي تفضلها ولماذا؟
وصف الخطوات اللازمة لحل عدم المساواة التربيعية بيانيًا.
وصف الخطوات اللازمة لحل عدم المساواة التربيعية جبريًا.

إجابة

1. قد تختلف الإجابات.

3. قد تختلف الإجابات.

فحص ذاتي

أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

هذا الشكل عبارة عن قائمة لتقييم فهمك للمفاهيم المقدمة في هذا القسم. يحتوي على 4 أعمدة تحمل علامة «يمكنني»، بكل ثقة، مع بعض المساعدة، ولا يمكنني الحصول عليها™! فيما يلي أستطيع، هناك حل المتباينات التربيعية بيانيًا وحل المتباينات التربيعية جبريًا. يتم ترك الأعمدة الأخرى فارغة لك للتحقق من فهمك. — الشكل 9.8.20

ب- على مقياس من 1 إلى 10، كيف تقيم إتقانك لهذا القسم في ضوء إجاباتك على قائمة التحقق؟ كيف يمكنك تحسين هذا؟

التمارين الرياضية\(\PageIndex{11}\) Solve Quadratic Inequalities Graphically

التمارين الرياضية\(\PageIndex{12}\) Solve Quadratic Inequalities Graphically

التمارين الرياضية\(\PageIndex{13}\) Writing Exercises