9.9: حل المتباينات التربيعية

Last updated

Nov 1, 2022
Page ID
201639
Save as PDF
- 9.8E: تمارين
- 9.9E: تمارين

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

حل عدم المساواة التربيعية بيانيًا
حل المتباينات التربيعية جبريًّا

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

حل: $2x−3=0$ .
إذا فاتتك هذه المشكلة، راجع مثال 2.2.
حل: $2y^{2}+y=15$ .
إذا فاتتك هذه المشكلة، راجع المثال 6.45.
حل $\frac{1}{x^{2}+2 x-8}>0$
إذا فاتتك هذه المشكلة، راجع المثال 7.56.

لقد تعلمنا كيفية حل عدم المساواة الخطية وعدم المساواة العقلانية سابقًا. كانت بعض التقنيات التي استخدمناها لحلها هي نفسها وبعضها كان مختلفًا. سنتعلم الآن حل المتباينات التي لها تعبير تربيعي. سوف نستخدم بعض التقنيات من حل عدم المساواة الخطية والعقلانية وكذلك المعادلات التربيعية. سنحل المتباينات التربيعية بطريقتين - بيانيًا وجبريًا.

حل المتباينات التربيعية بطريقة

تكون المعادلة التربيعية في الصورة القياسية عند كتابتها كـ $ax^{2}+bx+c=0$ . إذا استبدلنا علامة المساواة بعلامة عدم المساواة، فسيكون لدينا عدم مساواة تربيعية في الشكل القياسي.

تعريف $\PageIndex{1}$ : Quadratic Inequality

عدم المساواة التربيعية هي عدم مساواة تحتوي على تعبير تربيعي. يتم كتابة الشكل القياسي لعدم المساواة التربيعية:

$\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}$

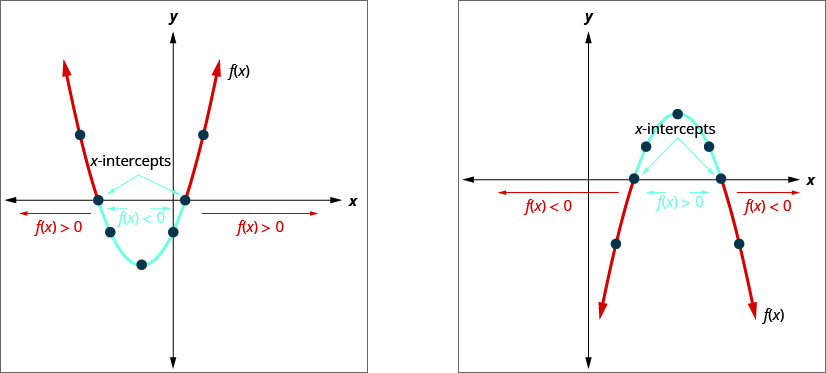
الرسم البياني للدالة التربيعية $f(x)=a x^{2}+b x+c=0$ هو المكافئ. عندما نسأل متى يكون $a x^{2}+b x+c<0$ ، فإننا نسأل متى يكون $f(x)<0$ . نريد أن نعرف متى يكون المكافئ أسفل $x$ المحور -.

عندما نسأل متى يكون $a x^{2}+b x+c>0$ ، فإننا نسأل متى يكون $f(x)>0$ . نريد أن نعرف متى يكون المكافئ فوق $y$ المحور -.

الرسم البياني الأول هو المكافئ المواجه لأعلى، f of x، على مستوى الإحداثيات x y. على يسار الدالة، يكون f of x أكبر من 0. بين تقاطعات x، يكون f of x أقل من 0. على يمين الدالة، يكون f of x أكبر من 0. الرسم البياني الثاني عبارة عن مكافئ متجه لأسفل، f من x، على مستوى إحداثي x y. على يسار الدالة، يكون f of x أقل من 0. بين تقاطعات x، يكون f of x أكبر من 0. على يمين الدالة، يكون f of x أقل من 0. — الشكل 9.8.1

مثال $\PageIndex{1}$ : How to Solve a Quadratic Inequality Graphically

حل $x^{2}−6x+8<0$ بيانيًا. اكتب الحل بالتدوين الفاصل الزمني.

الحل:

الخطوة 1: اكتب عدم المساواة التربيعية في النموذج القياسي.

عدم المساواة في الشكل القياسي.

$x^{2}-6 x+8<0$

الخطوة 2: رسم بياني للدالة $f(x)=a x^{2}+b x+c$ باستخدام الخصائص أو التحويلات.

سنقوم بالرسم البياني باستخدام الخصائص.

$f(x)=x^{2}-6 x+8$

انظر $a$ إلى المعادلة.

$\color{red}{a=1, b=-6, c=8}$

$f(x)=x^{2}-6 x+8$

نظرًا $a$ لأنه إيجابي، فإن القطع المكافئ يفتح لأعلى.

يفتح القطع المكافئ لأعلى.

$f(x)=x^{2}-6 x+8$

محور التماثل هو الخط $x=-\frac{b}{2 a}$ .

محور التماثل

$x=-\frac{b}{2 a}$

$\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}$

محور التماثل هو الخط $x=3$ .

تقع قمة الرأس على محور التماثل. $x=3$ استبدل الوظيفة.

فيرتكس

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}$

قمة الرأس هي $(3,-1)$ .

نحن نجد $f(0)$

$y$ -اعتراض

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}$

$y$ الاعتراض الإلكتروني هو $(0.8)$ .

نستخدم محور التماثل لإيجاد نقطة متماثلة للجزء $y$ المقطوع. $y$ التقاطع -هو $3$ الوحدات اليسرى من محور التماثل، $x=3$ . $3$ تحتوي الوحدات النقطية الموجودة على يمين محور التماثل على $x=6$ .

نقطة متماثلة إلى $y$ نقطة التقاطع

النقطة هي $(6,8)$ .

نحن نحل $f(x)=0$ .

$x$ - عمليات الاعتراض

يمكننا حل هذه المعادلة التربيعية عن طريق التحليل.

$\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}$

$x$ عمليات الاعتراض - هي $(2,0)$ و $(4,0)$ .

نحن نرسم قمة الرأس والاعتراض والنقطة المتماثلة للنقطة $y$ الفاصلة. نقوم بتوصيل هذه $5$ النقاط لرسم القطع المكافئ.

الخطوة 3: حدد الحل من الرسم البياني.

$x^{2}-6 x+8<0$

يطلب عدم المساواة القيم $x$ التي تجعل الدالة أقل من $0$ . ما القيم التي $x$ تجعل القطع المكافئ أسفل $x$ المحور -.

نحن لا ندرج القيم $2$ ، $4$ لأن عدم المساواة أقل من فقط.

الحل، في الترميز الفاصل الزمني، هو $(2,4)$ .

التمارين $\PageIndex{1}$

حل $x^{2}+2 x-8<0$ بيانيًا
اكتب الحل بالتدوين الفاصل الزمني

إجابة

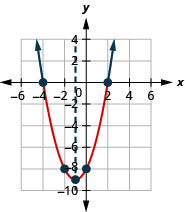
$يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له رأس (سالب 2، سالب 9)، نقطة التقاطع y (0، 8)، ومحور التماثل الموضح عند x يساوي سالب 2.$
الشكل 9.8.4
$(-4,2)$

التمارين $\PageIndex{2}$

حل $x^{2}-8 x+12 \geq 0$ بيانيًا
اكتب الحل بالتدوين الفاصل الزمني

إجابة

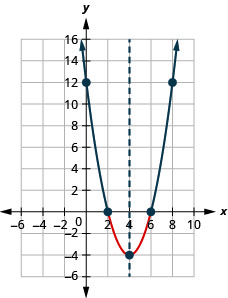
$يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. وتتكون قممها من (4، سالب 4) وقطرتها x مقدارها (2، 0) و (6، 0).$
الشكل 9.8.5
$(-\infty, 2] \cup[6, \infty)$

نسرد الخطوات التي يجب اتخاذها لحل عدم المساواة التربيعية بيانيًا.

حل عدم المساواة التربيعية بيانيًّا

اكتب عدم المساواة التربيعية في الصورة القياسية.
رسم بياني للدالة $f(x)=ax^{2}+bx+c$ .
حدد الحل من الرسم البياني.

في المثال الأخير، تم فتح القطع المكافئ لأعلى وفي المثال التالي، يفتح لأسفل. في كلتا الحالتين، نبحث عن جزء القطع المكافئ الموجود أسفل $x$ المحور -ولكن نلاحظ كيف يؤثر موضع القطع المكافئ على المحلول.

مثال $\PageIndex{2}$

حل $-x^{2}-8 x-12 \leq 0$ بيانيًا. اكتب الحل بالتدوين الفاصل الزمني.

الحل:

الجدول 9.8.1
عدم المساواة التربيعية في الشكل القياسي.	$-x^{2}-8 x-12 \leq 0$
رسم بياني للدالة $f(x)=-x^{2}-8 x-12$	يفتح القطع المكافئ لأسفل. $.$ الشكل 9.8.6
أوجد خط التماثل.	$\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}$
ابحث عن قمة الرأس.	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}$ فيرتكس $(-4,4)$
ابحث عن $x$ -Intercepts. دعونا $f(x)=0$ .	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}$
العامل: استخدم خاصية المنتج الصفري.	$\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}$
رسم بياني القطع المكافئ.	$x$ - عمليات الاعتراض $(-6,0), (-2.0)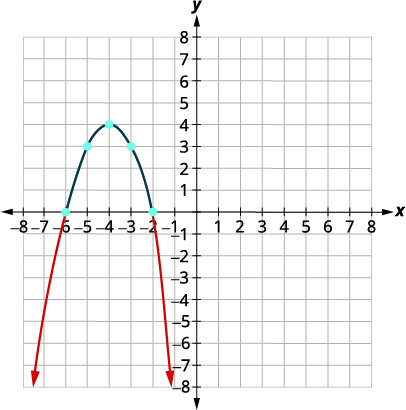$ $.$ الشكل 9.8.7
حدد الحل من الرسم البياني. نقوم بتضمين $x$ -intercepts لأن عدم المساواة «أقل من أو يساوي».	$(-\infty,-6] \cup[-2, \infty)$

التمارين $\PageIndex{3}$

حل $-x^{2}-6 x-5>0$ بيانيًا
اكتب الحل بالتدوين الفاصل الزمني

إجابة

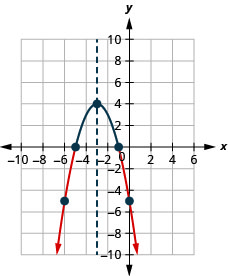
$شكل مكافئ متجه لأسفل على مستوى الإحداثيات x y. له رأس (سالب 3، 4)، ومقطع y عند (0، سالب 5)، ومحور التماثل الموضح عند x يساوي سالب 3.$
الشكل 9.8.8
$(-5,-1)$

التمارين $\PageIndex{4}$

حل $−x^{2}+10x−16≤0$ بيانيًا
اكتب الحل بالتدوين الفاصل الزمني

إجابة

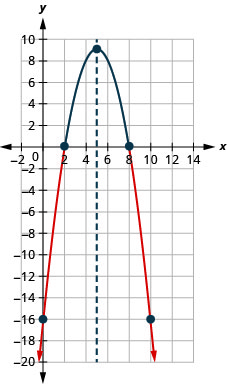
$شكل مكافئ متجه لأسفل على مستوى الإحداثيات x y. له رأس (٥، ٩)، نقطة تقاطع ص عند (٠، سالب ١٦)، ومحور التماثل س يساوي ٥.$
الشكل 9.8.9
$(-\infty, 2] \cup[8, \infty)$

حل المتباينات التربيعية جبريًّا

الطريقة الجبرية التي سنستخدمها تشبه إلى حد كبير الطريقة التي استخدمناها لحل عدم المساواة العقلانية. سنجد النقاط الحرجة لعدم المساواة، والتي ستكون الحلول للمعادلة التربيعية ذات الصلة. تذكر أن التعبير متعدد الحدود يمكنه تغيير العلامات فقط عندما يكون التعبير صفرًا.

سنستخدم النقاط الحرجة لتقسيم خط الأعداد إلى فترات ثم نحدد ما إذا كان التعبير التربيعي سيكون موجبًا أم سالبًا في الفاصل الزمني. ثم نحدد الحل لعدم المساواة.

مثال $\PageIndex{3}$ : How to Solve Quadratic Inequalities Algebraically

حل $x^{2}-x-12 \geq 0$ جبريًا. اكتب الحل بالتدوين الفاصل الزمني.

الحل:

الجدول 9-8-2
الخطوة 1: اكتب عدم المساواة التربيعية في النموذج القياسي.	عدم المساواة في الشكل القياسي.	$x^{2}-x-12 \geq 0$
الخطوة 2: تحديد النقاط الحرجة - حلول المعادلة التربيعية ذات الصلة.	قم بتغيير علامة عدم المساواة إلى علامة المساواة ثم حل المعادلة.	$\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}$
الخطوة 3: استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فترات.	استخدم $-3$ خط الأرقام وقسمه $4$ إلى فترات.	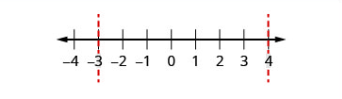$لقطة شاشة (4) .png$
الخطوة 4: فوق خط الأرقام تظهر علامة كل تعبير تربيعي باستخدام نقاط الاختبار من كل فاصل زمني مستبدل من عدم المساواة الأصلية.	الاختبار: $x=-5$ $x=0$ $x=5$	$\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}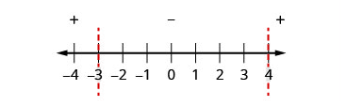$ $لقطة شاشة (5) .png$ الشكل 9.8.11
الخطوة 5: تحديد الفواصل الزمنية التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.	$x^{2}-x-12 \geq 0$ يكون عدم المساواة إيجابيًا في الفترتين الأولى والأخيرة ويساوي $0$ عند النقاط $-4,3$ .	الحل، في الترميز الفاصل الزمني، هو $(-\infty,-3] \cup[4, \infty)$ .

التمارين $\PageIndex{5}$

حل $x^{2}+2x−8≥0$ جبريًا. اكتب الحل بالتدوين الفاصل الزمني.

إجابة: $(-\infty,-4] \cup[2, \infty)$

التمارين $\PageIndex{6}$

حل $x^{2}−2x−15≤0$ جبريًا. اكتب الحل بالتدوين الفاصل الزمني.

إجابة: $[-3,5]$

في هذا المثال، نظرًا لأن $x^{2}−x−12$ عوامل التعبير جيدة، يمكننا أيضًا العثور على العلامة في كل فاصل زمني مثلما فعلنا عندما قمنا بحل عدم المساواة العقلانية. نجد علامة كل عامل من العوامل، ثم علامة المنتج. سيكون خط الأرقام الخاص بنا مثل هذا:

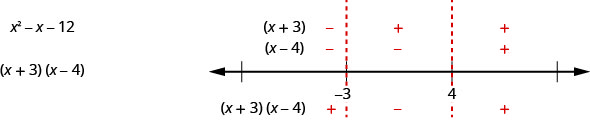
يوضح الشكل التعبير x التربيعي ناقص x ناقص 12 مع احتساب كمية x زائد 3 أضعاف كمية x ناقص 4. تُظهر الصورة خط أرقام يوضح الخطوط المنقطة على سالب 3 و4. يُظهر أن علامات الكمية x plus 3 سلبية وإيجابية وإيجابية، وعلامات الكمية x ناقص 4 سلبية وسلبية وإيجابية. تحت خط الأعداد، تُظهر الكمية x زائد 3 أضعاف الكمية x ناقص 4 مع العلامات الإيجابية والسلبية والإيجابية. — الشكل 9.8.12

النتيجة هي نفسها التي وجدناها باستخدام الطريقة الأخرى.

نحن نلخص الخطوات هنا.

حل المتباينات التربيعية جبريًّا

اكتب عدم المساواة التربيعية في الصورة القياسية.
حدد النقاط الحرجة - حلول المعادلة التربيعية ذات الصلة.
استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فترات.
تظهر فوق خط الأعداد علامة كل تعبير تربيعي باستخدام نقاط الاختبار من كل فاصل زمني يتم استبداله في عدم المساواة الأصلية.
حدد الفترات التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.

مثال $\PageIndex{4}$

حل $x^{2}+6x−7≥0$ جبريًا. اكتب الحل بالتدوين الفاصل الزمني.

الحل:

الجدول 9-8-3
اكتب عدم المساواة التربيعية في الصورة القياسية.	$-x^{2}+6 x-7 \geq 0$
اضرب كلا جانبي عدم المساواة في $-1$ . تذكر عكس علامة عدم المساواة.	$x^{2}-6 x+7 \leq 0$
أوجد النقاط الحرجة عن طريق حل المعادلة التربيعية ذات الصلة.	$x^{2}-6 x+7=0$
اكتب الصيغة التربيعية.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
ثم استبدل قيم $a, b, c$ .	$x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}$
قم بالتبسيط.	$x=\frac{6 \pm \sqrt{8}}{2}$
قم بتبسيط الراديكالية.	$x=\frac{6 \pm 2 \sqrt{2}}{2}$
قم بإزالة العامل المشترك، $2$ .	$\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}$
استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فترات. أرقام الاختبار من كل فاصل زمني في عدم المساواة الأصلية.	$.$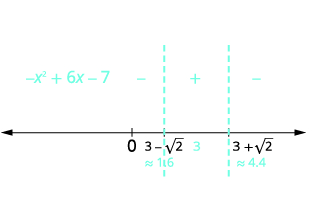
حدد الفترات التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.	$-x^{2}+6 x-7 \geq 0$ في الفترة المتوسطة $[3-\sqrt{2}, 3+\sqrt{2}]$

التمارين $\PageIndex{7}$

حل $−x^{2}+2x+1≥0$ جبريًا. اكتب الحل بالتدوين الفاصل الزمني.

إجابة: $[-1-\sqrt{2},-1+\sqrt{2}]$

التمارين $\PageIndex{8}$

حل $−x^{2}+8x−14<0$ جبريًا. اكتب الحل بالتدوين الفاصل الزمني.

إجابة: $(-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)$

كانت حلول عدم المساواة التربيعية في كل من الأمثلة السابقة إما عبارة عن فاصل زمني أو اتحاد بين فترتين. نتج هذا عن حقيقة أننا وجدنا في كل حالة حلين للمعادلة التربيعية المقابلة $ax^{2}+bx+c=0$ . ثم أعطانا هذان الحلان إما القطعتين $x$ المتقاطعتين للرسم البياني أو النقطتين الحرجتين لتقسيم خط الأعداد إلى فواصل زمنية.

يرتبط هذا بمناقشتنا السابقة لعدد ونوع الحلول للمعادلة التربيعية باستخدام التمييز.

للمعادلة التربيعية للنموذج $ax^{2}+bc+c=0, a≠0$ .

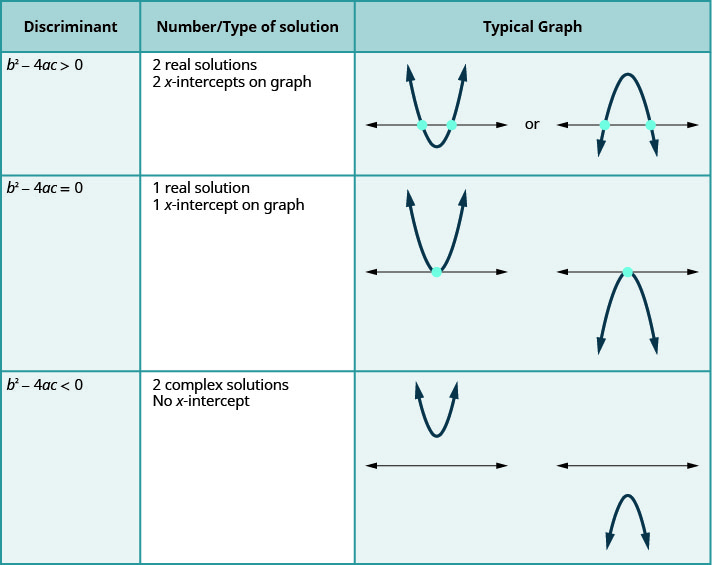
الشكل عبارة عن جدول يحتوي على 3 أعمدة. تم تصنيف العمود 1 بأنه تمييزي، والعمود 2 هو رقم/نوع الحل، والعمود 3 هو الرسم البياني النموذجي. عند القراءة عبر الأعمدة، إذا كان b squared ناقص 4 مرات في c أكبر من 0، فسيكون هناك حلان حقيقيان نظرًا لوجود نقطتي تقاطع x على الرسم البياني. صورة رسم بياني نموذجي: مكافئ صعودي أو هبوطي مع قطعتي اعتراض x. إذا كان التمييز b المربع ناقص 4 مرات في c يساوي 0، فسيكون هناك حل حقيقي واحد نظرًا لوجود تقاطع x واحد على الرسم البياني. صورة الرسم البياني النموذجي عبارة عن قطع مكافئ متجه لأعلى أو لأسفل وله قمة على المحور السيني بدلاً من عبوره. إذا كان مقياس التمييز b المربع ناقص 4 مرات في c أقل من 0، فهناك حلان معقدان لعدم وجود التقاطع السيني. تُظهر صورة الرسم البياني النموذجي القطع المكافئ المواجه لأعلى أو لأسفل ولا يعبر المحور السيني. — الشكل 9.8.14

يوضح لنا الصف الأخير من الجدول عندما لا تتقاطع البارابولاس أبدًا مع $x$ المحور -. باستخدام الصيغة التربيعية لحل المعادلة التربيعية، يكون الجذر سالبًا. نحصل على حلين معقدين.

في المثال التالي، ستنتج حلول عدم المساواة التربيعية عن حل المعادلة التربيعية الذي يكون معقدًا.

مثال $\PageIndex{5}$

حل، اكتب أي حل في الترميز الفاصل الزمني:

$x^{2}-3 x+4>0$
$x^{2}-3 x+4 \leq 0$

الحل:

أ.

الجدول 9-8-4
اكتب عدم المساواة التربيعية في الصورة القياسية.	$-x^{2}-3 x+4>0$
أوجد النقاط الحرجة عن طريق حل المعادلة التربيعية ذات الصلة.	$x^{2}-3 x+4=0$
اكتب الصيغة التربيعية.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
ثم استبدل قيم $a, b, c$ .	$x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}$
قم بالتبسيط.	$x=\frac{3 \pm \sqrt{-7}}{2}$
قم بتبسيط الراديكوند.	$x=\frac{3 \pm \sqrt{7 i}}{2}$
تخبرنا الحلول المعقدة أن القطع المكافئ لا يعترض $x$ المحور السيني. أيضًا، ينفتح المكافئ لأعلى. يخبرنا هذا أن القطع المكافئ أعلى تمامًا من $x$ المحور -.	حلول معقدة 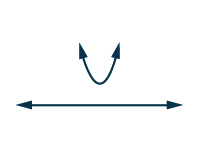$.$ الشكل 9.8.15

علينا أن نجد الحل لـ $x^{2}−3x+4>0$ . نظرًا لأن جميع قيم $x$ الرسم البياني أعلى من $x$ المحور -، فإن جميع القيم $x$ تجعل عدم المساواة حقيقة. نكتب في تدوين الفاصل الزمني $(−∞,∞)$ .

ب. اكتب عدم المساواة التربيعية في الصورة القياسية.

$x^{2}-3 x+4 \leq 0$

أوجد النقاط الحرجة عن طريق حل المعادلة التربيعية ذات الصلة.

$x^{2}-3 x+4=0$

نظرًا لأن المعادلة التربيعية المقابلة هي نفسها الموجودة في الجزء (أ)، فإن المكافئ سيكون هو نفسه. ينفتح القطع المكافئ لأعلى ويكون أعلى تمامًا من $x$ المحور - ولا يوجد جزء منه أسفل $x$ المحور.

علينا أن نجد الحل لـ $x^{2}−3x+4≤0$ . نظرًا لأن جميع قيم $x$ الرسم البياني لا تقل أبدًا عن $x$ المحور -، فلا توجد قيم $x$ تجعل عدم المساواة حقيقة. لا يوجد حل لعدم المساواة.

التمارين $\PageIndex{9}$

حل واكتب أي حل في الترميز الفاصل الزمني:

$-x^{2}+2 x-4 \leq 0$
$-x^{2}+2 x-4 \geq 0$

إجابة

$(-\infty, \infty)$
لا يوجد حل

التمارين $\PageIndex{10}$

حل واكتب أي حل في الترميز الفاصل الزمني:

$x^{2}+3 x+3<0$
$x^{2}+3 x+3>0$

إجابة

لا يوجد حل
$(-\infty, \infty)$

المفاهيم الرئيسية

حل عدم المساواة التربيعية بيانيًّا
1. اكتب عدم المساواة التربيعية في الصورة القياسية.
2. قم برسم بياني $f(x)=ax^{2}+bx+c$ للدالة باستخدام الخصائص أو التحويلات.
3. حدد الحل من الرسم البياني.
كيفية حل عدم المساواة التربيعية جبريًّا
1. اكتب عدم المساواة التربيعية في الصورة القياسية.
2. حدد النقاط الحرجة - حلول المعادلة التربيعية ذات الصلة.
3. استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فترات.
4. تظهر فوق خط الأعداد علامة كل تعبير تربيعي باستخدام نقاط الاختبار من كل فاصل زمني يتم استبداله في عدم المساواة الأصلية.
5. حدد الفترات التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.

مسرد المصطلحات

عدم المساواة التربيعية: عدم المساواة التربيعية هي عدم مساواة تحتوي على تعبير تربيعي.

أهداف التعلم

حل المتباينات التربيعية بطريقة

تعريف9.9.1\PageIndex{1}: Quadratic Inequality

مثال9.9.1\PageIndex{1}: How to Solve a Quadratic Inequality Graphically

التمارين9.9.1\PageIndex{1}

التمارين9.9.2\PageIndex{2}

حل عدم المساواة التربيعية بيانيًّا

مثال9.9.2\PageIndex{2}

التمارين9.9.3\PageIndex{3}

التمارين9.9.4\PageIndex{4}

حل المتباينات التربيعية جبريًّا

مثال9.9.3\PageIndex{3}: How to Solve Quadratic Inequalities Algebraically

التمارين9.9.5\PageIndex{5}

التمارين9.9.6\PageIndex{6}

حل المتباينات التربيعية جبريًّا

مثال9.9.4\PageIndex{4}

التمارين9.9.7\PageIndex{7}

التمارين9.9.8\PageIndex{8}

مثال9.9.5\PageIndex{5}

التمارين9.9.9\PageIndex{9}

التمارين9.9.10\PageIndex{10}

المفاهيم الرئيسية

مسرد المصطلحات

تعريف $\PageIndex{1}$ : Quadratic Inequality

مثال $\PageIndex{1}$ : How to Solve a Quadratic Inequality Graphically

التمارين $\PageIndex{1}$

التمارين $\PageIndex{2}$

مثال $\PageIndex{2}$

التمارين $\PageIndex{3}$

التمارين $\PageIndex{4}$

مثال $\PageIndex{3}$ : How to Solve Quadratic Inequalities Algebraically

التمارين $\PageIndex{5}$

التمارين $\PageIndex{6}$

مثال $\PageIndex{4}$

التمارين $\PageIndex{7}$

التمارين $\PageIndex{8}$

مثال $\PageIndex{5}$

التمارين $\PageIndex{9}$

التمارين $\PageIndex{10}$